一种自适应轴对称FEM-SPH 耦合算法及其在高速冲击模拟中的应用*

肖毅华，胡德安，韩 旭，杨 刚

(湖南大学汽车车身先进设计制造国家重点实验室，湖南 长沙410082)

高速冲击涉及材料的大变形、破碎和飞溅等现象，应用基于网格的方法对其进行数值模拟存在困难。拉格朗日网格方法会遭遇单元畸变而计算终止;单元侵蚀技术可以克服畸变问题，但会导致能量损失并且改变物质的几何边界。欧拉网格方法难于精确地捕捉物质界面和跟踪材料的历史数据。光滑粒子流体动力学(SPH)［1-2］作为一种无网格、拉格朗日粒子法，能克服基于网格的方法的缺陷。SPH 在处理大变形方面较有限元法(FEM)等拉格朗日网格方法有优势，但在模拟小变形时的计算精度和效率都不及FEM，并且SPH 的边界处理不如FEM 方便。对于高速冲击问题，由于大变形通常只发生在有限的局部区域，耦合FEM 和SPH 是一种十分有效的模拟途径。在绝大部分的小变形区域内用FEM 计算，在局部的大变形区域内用SPH 计算，这样既能保证计算精度又能提高计算效率。目前，一些研究者［3-10］对FEM-SPH 耦合算法及其在高速冲击问题中的应用进行了研究，并取得了一些有意义的结果。

本文中，提出一种自适应轴对称FEM-SPH 耦合算法，并用于高速冲击模拟。该算法自动将畸变单元转化为粒子，既能避免单元畸变，又尽可能地减小SPH 计算区域。文献［4-6，9］也给出了类似的算法，本文算法与它们的主要区别在于:提出一种新的耦合算法，实现单元和粒子计算的高精度耦合;提出采用最小内角转化准则和单元分组转化方式来实现单元向粒子的自动转化。通过计算应力波传播、泰勒杆撞击问题，验证算法的正确性;并通过模拟弹丸侵彻铝板和混凝土问题，说明算法在高速冲击模拟中的可靠性和实用性。

1 基本方程

为了求解轴对称高速冲击问题，采用如下形式的轴对称SPH 方程

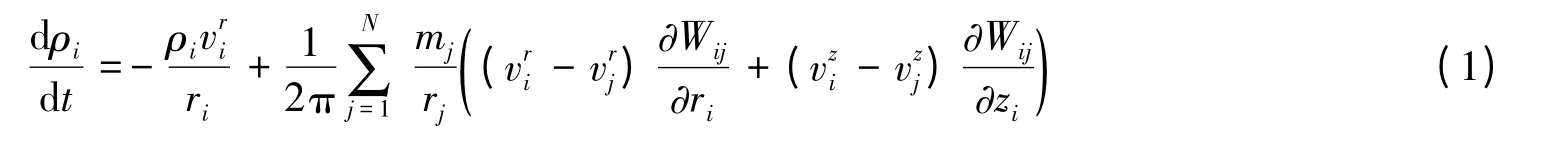
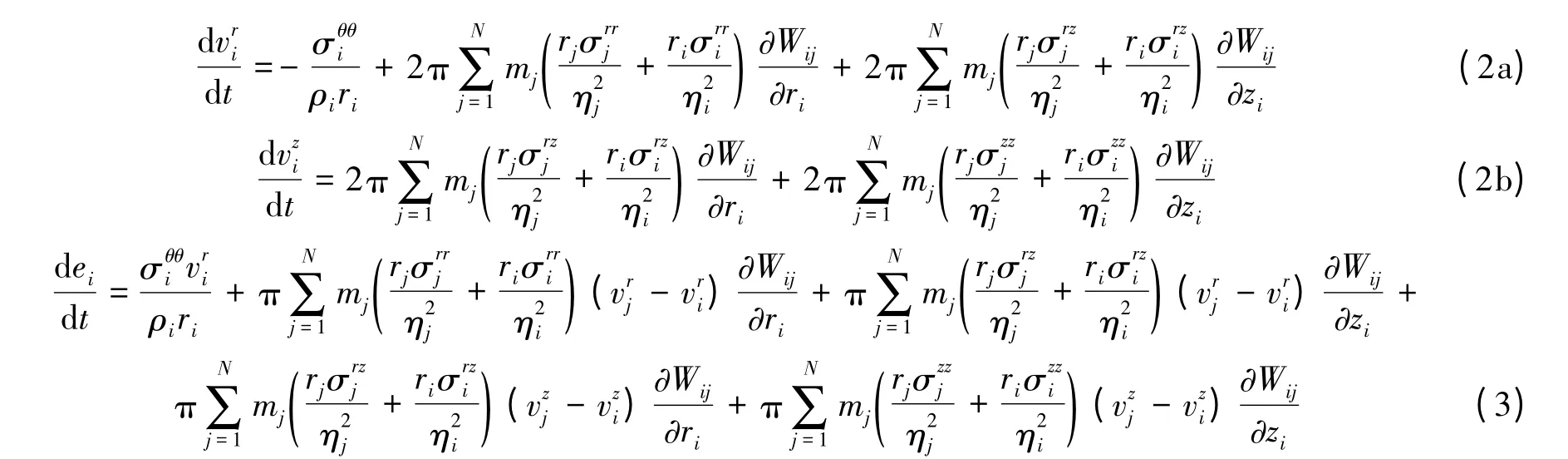
式中:ρ 为三维密度，η=2πrρ 为平面密度，m 为质量，v 为速度，σ 为应力，e 为质量内能，r 和z 分别为径向和轴向坐标，W 为光滑函数。光滑函数选择为B 样条函数［11］。初始光滑长度

式中:αh为光滑长度放大因子，Δ 为粒子间距。光滑长度在计算中保持不变。为了稳定计算、消除数值振荡，SPH 法采用文献［12］中的结合型人工粘性。关于求解冲击动力问题的轴对称FEM 的基本方程，参考文献［13］。

2 FEM 与SPH 的自适应耦合

为了实现FEM 和SPH 的自适应耦合，需要处理3 个关键问题:(1)同一物体中的单元与粒子的耦合;(2)单元与单元、单元与粒子以及粒子与粒子的接触;(3)单元向粒子的自动转化。下面介绍对上述3 个问题的处理方法。

2.1 单元-粒子耦合界面处理

本文中提出一种新的高精度耦合算法，图1 为该算法的示意图。耦合算法的关键是计算耦合界面附近单元与粒子间的相互作用力。本文算法计算相互作用力的基本思想是:一方面，将耦合界面附近的单元作为虚粒子包含到SPH 方程中，得到邻近单元对粒子的作用力;另一方面，根据耦合界面附近的粒子应力确定作用在耦合界面上的单元边上的等效面力，再将这些面力等效到单元节点上，最终得到邻近粒子对单元节点的作用力。

耦合界面附近被粒子的影响域覆盖的单元(以下称耦合界面单元)作为虚粒子处理。每一个耦合界面单元作为一个虚粒子。图2为虚粒子生成示意图。虚粒子的变量在每一个时间步都根据所在单元的相关变量重新确定，质量和密度与对应单元的质量和密度相等，坐标和速度取为单元3 个节点的相应值的算术平均值，应力与单元的应力相等。虚粒子的半径和光滑长度按下述方式确定

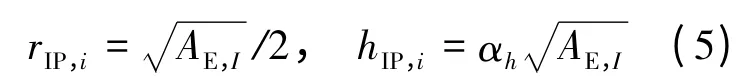
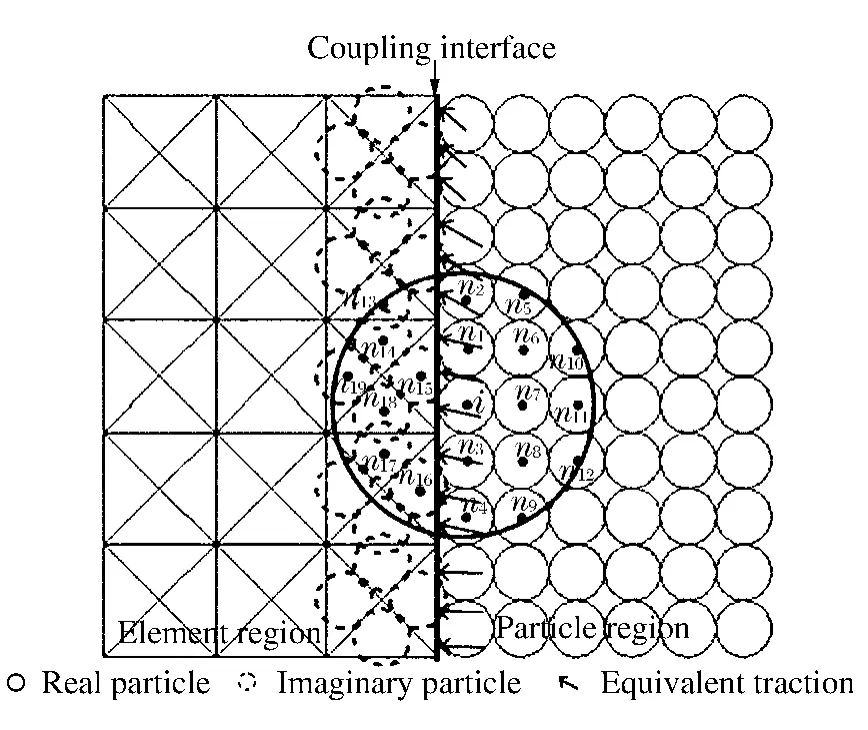
图1 单元-粒子耦合算法示意图Fig.1 Description of the element-particle coupling algorithm

图2 虚粒子生成示意图Fig.2 Description of the generation of imaginary particles

式中:rIP，i和hIP，i分别为虚粒子半径和光滑长度，AE，I为虚粒子所在单元的面积，αh的含义同式(4)中的αh。

计算邻近单元对粒子的作用力只需将虚粒子包含到SPH 计算中。如图1 所示，粒子i 的影响域内包含实粒子(n1，…，n12)和虚粒子(n13，…，n19)。计算粒子i 时，实粒子和虚粒子都参与SPH 方程(1)～(3)的求和，SPH 方程的形式不发生改变。这样，在动量方程(2a)和(2b)中，虚粒子的贡献即为邻近单元对粒子的作用力。另外，虚粒子也应用于粒子的应变率的计算。这可以克服SPH 近似的边界缺陷，提高近似精度，使应变率和应力计算更准确。

图3 为计算邻近粒子对单元节点的作用力的示意图。对于每一条位于耦合界面的单元边，根据与它关联的粒子的应力确定一个等效面力，并认为其均匀作用在单元边上。等效面力的计算方式为

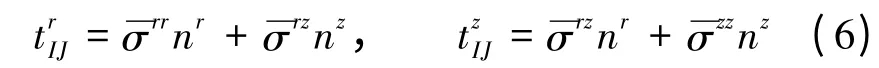
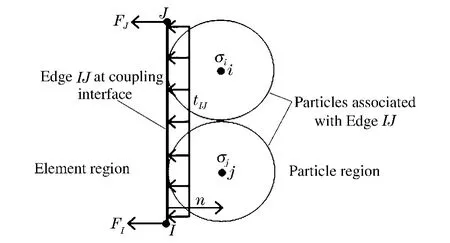
图3 邻近粒子对单元节点的作用力的计算Fig.3 Calculation of the forces on element nodes from adjacent particles

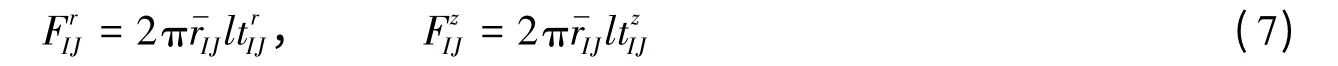
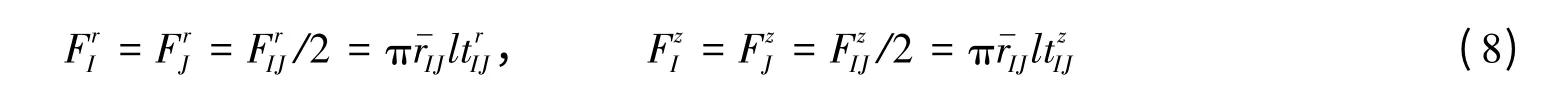
2.2 接触界面处理

不同物体或者同一物体的不同部分间存在接触作用，需要采用有效的算法进行处理，防止出现非物理的穿透。目前，已有一些较好的算法来处理各种类型的接触，本文中基于已有接触算法来进行接触界面计算。对于单元与单元间的接触，采用G.R.Johnson 等［14］提出的对称接触和滑移界面算法处理。对于单元与粒子间的接触，参考G.R.Johnson 等［15］处理GPA 节点与单元接触的算法处理。对于粒子与粒子间的接触，参照J.C.Campbell 等［16］提出的粒子-粒子型罚接触算法处理。

2.3 单元向粒子的自动转化

为实现单元自动转化为粒子，首先必须确定需要转化为粒子的畸变单元(以下简称转化单元)。本文中中采用三角形单元计算，其最小内角能很好地反映单元的畸变程度。因此，我们提出采用最小内角转化准则来确定转化单元，即:如果某一单元的最小内角小于指定的临界值θc时，则该单元为转化单元;否则该单元无需转化。本文中，取θc=30°。

在确定转化单元时，除了采用最小内角转化准则，还结合了一种分组转化方式。图4 为单元分组转化的示意图。每个物体内的单元在计算的初始化阶段分成单元组。在计算过程中，如果一个单元组中存在一个单元满足最小内角转化准则，则该组中的所有单元均作为转化单元。使用分组转化的好处是:快速地搜索到耦合界面单元，提高计算效率;同时，使耦合界面的几何更连续和规则，提高计算精度和稳定性。单元分组的过程很简单。首先找到包含物体的最小矩形域;然后，将矩形域划分为参考尺寸为Δs的矩形子域。Δs的大小为

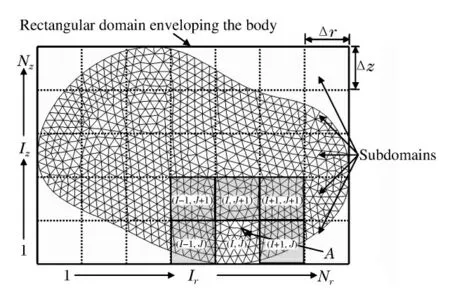
图4 单元分组转化Fig.4 Group-based conversion of elements

式中:κ 为大于1 的因数，它使单元组转化生成的粒子的影响域不会超出其邻接单元组覆盖的范围，本文计算取κ=1.5;Rmax为最大可能的粒子影响域半径，按下式估计

式中:A0，max为初始时刻单元的最大面积。根据确定的Δs，计算沿径向和轴向的矩形子域数目分别为

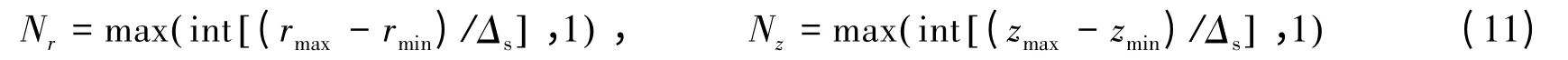
然后，可以计算矩形子域在径向和轴向的精确尺寸为

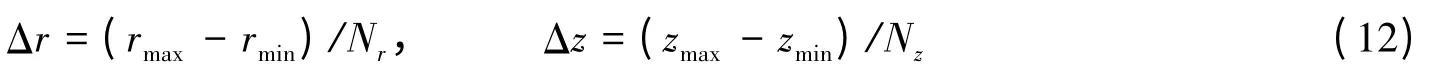
将矩形子域编号为(Ir，Iz)，Ir和Iz分别表示矩形子域沿径向和轴向的序号，取值分别为1 ～Nr和1～Nz。根据此编号方式，容易确定一个单元所在的矩形子域的编号为

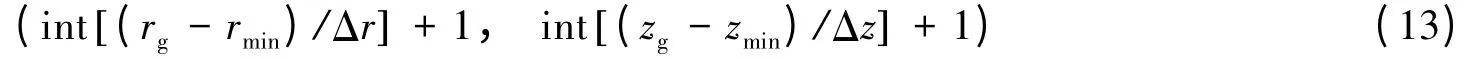
式中:(rg，zg)为单元的重心坐标。由式(13)确定每个单元所在的矩形子域，同一矩形子域中的单元为一个单元组。

采用上述方式确定转化单元后，将这些单元从单元列表中删除，并且增加新的粒子。新增粒子的变量的确定方式与前述虚粒子相同。与虚粒子不同的是，这些粒子产生后，在后续计算中其变量通过SPH 方程计算。

转化单元变成粒子后，单元区域与粒子区域的耦合界面发生变化，需更新耦合界面单元以用于耦合计算。图4 说明了使用分组转化时如何快速地搜索到耦合界面单元。例如，单元组(I，J)中的单元A 满足最小内角转化准则，则单元组(I，J)中的所有单元转化为粒子，而单元组(I，J)的邻接单元组中的单元作为耦合界面单元。根据单元组的编号规则，单元组(I，J)的邻接单元组容易确定为

转化单元变成粒子后，单元区域表面也需更新。图5 为图4 中单元A 所在的单元组。该单元组表面包含位于单元区域表面的线段N1N2，N2N3，…，N5N6和内部的线段N6N7，N7N8，…，N24N1。当该单元组内的单元转化为粒子后，线段N1N2，N2N3，…，N5N6从单元区域表面中删除，而线段N6N7，N7N8，…N24N1增加到单元区域表面中去。单元区域表面更新后，单元边与粒子间的关联也相应更新。与位于线段N1N2，N2N3，…，N5N6上的单元边关联的粒子被释放;由连接到线段N6N7，N7N8，…，N24N1的单元转化生成的粒子需要关联到该线段上的单元边。确定新生成的粒子与单元边的关联时，存在图5 中类似单元A 和B 的2 种典型情况。单元A 只有1 条边(N6N7)位于新增的单元区域表面上，由单元A 生成的粒子与边N6N7关联，并且与该边固连，不允许与其发生分离或相对滑移。单元B 有2 条边(N8N9和N9N10)位于新增的单元区域表面上，由单元B 生成的粒子同时与边N8N9和N9N10关联，但只与两者中距离最近的边固连。为实现粒子与单元边的固连，本文中应用G.R.Johnson 等［15］连接GPA 节点与单元边的算法。

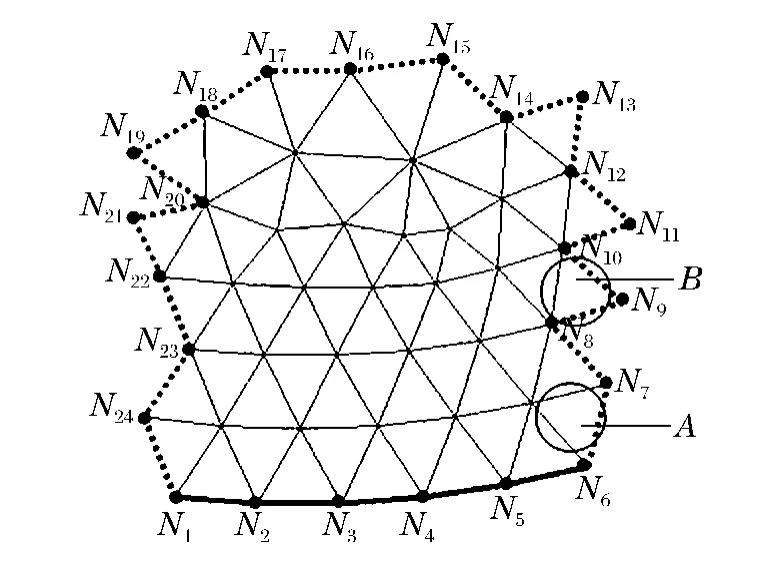
图5 单元区域表面和单元边与粒子间关联的更新Fig.5 Update of surfaces of element regions and association between element sides and particles

3 数值算例

3.1 弹性杆中的应力波传播

如图6(a)所示，半径1 mm、长20 mm 的弹性杆以50 m/s 速度垂直撞击刚性面。弹性杆的材料参数为:密度ρ=7.85 g/cm3，杨氏模量E=206 GPa，泊松比ν=0.3。由于弹性杆具有大长径比，本问题近似为一维应力问题，可以得到解析解，为验证算法提供参考。采用耦合算法和有限元法计算此问题，并将计算结果与解析解进行对比。图6(b)为耦合计算的模型，弹性杆的上、下两半分别采用1 000 个粒子和1 000 个单元离散。有限元法采用2 000 个单元离散弹性杆，单元的分布形式与耦合计算模型相同。有限元求解采用LS-DYNA 软件。

图7 为计算得到的3 μs 时沿轴线r=0.5 mm 的应力分布。本文耦合算法的计算结果与DYNA 计算结果符合很好，耦合界面处的应力很光滑，应力波准确地传播通过耦合界面。耦合算法计算的应力波幅值和前沿位置与一维解析解也基本相符，只是由于采用二维轴对称计算，存在弥散效应，所以应力有一定振荡。由上述计算结果可见，本文提出的耦合算法是比较精确的。

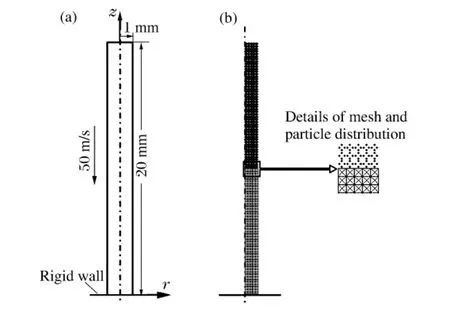
图6 弹性杆撞击刚性面的模型Fig.6 Model of elastic bar impacting a rigid wall

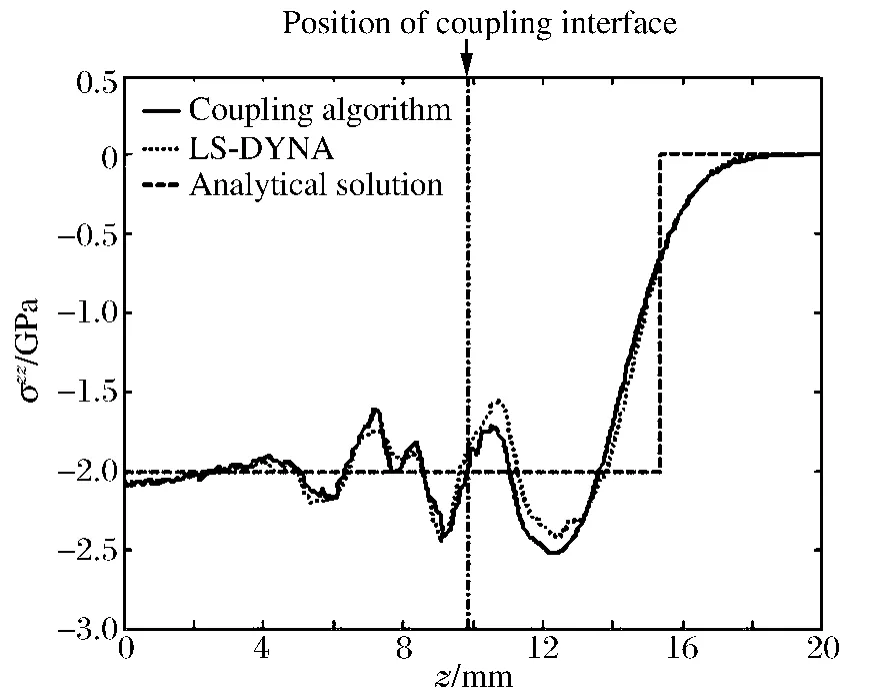
图7 3 μs 时沿轴线r=0.5 mm 的应力分布Fig.7 Stress distributions along the axis of r=0.5mm at 3 μs

3.2 泰勒杆

泰勒杆实验是采用金属圆杆高速正撞击刚性平面，经常被用来研究材料的本构模型和验证数值算法的准确性。采用本文的自适应耦合算法对泰勒杆实验进行模拟，将模拟结果与实验结果对比，验证本文算法的准确性。本文中模拟的泰勒杆实验为:直径D0=7.6 mm、长度L0=25.4 mm 的阿姆克铁圆杆以221 m/s 的速度正撞击刚性面。模拟中，将阿姆克铁视为理想弹塑性材料，使用Mie-Grüneisen 状态方程计算材料压力，相关的材料特性参数取自文献［17］。圆杆在初始时刻采用2 680 个单元离散。

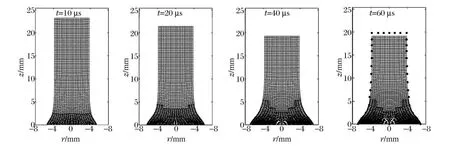
图8 圆杆在不同时刻的变形Fig.8 Deformation of the cylinder at different time

图8 为自适应耦合算法计算的圆杆在10、20、40 和60 μs 等4 个时刻的变形图。由该图可见，圆杆下端的单元随着变形的发展逐渐转化为粒子;转化形成的粒子区域具有很好的连续性，粒子区域和单元区域间的耦合界面较规则。计算在60 μs 时终止，此时圆杆几乎不再变形。在60 μs 时刻的变形图中，对比了计算的圆杆变形形状与实验结果［18］(黑点表示)，两者符合较好。计算的圆杆体变形后的特征尺寸为:长度Lc=19.1 mm，撞击端直径Dc=13.9 mm，离撞击端0.2L0处的宽度Wc=8.6 mm;相应的实验结果［18］依次为Le=19.8 mm，De=13.7 mm，We=8.6 mm;两者的平均相对误差(ε=(|Lc-Le|/Le+|Dc-De|/De+|Wc-We|/We)/3)不到2%。计算的圆杆长度略小于实验结果，其误差相对于其他2 个特征尺寸的误差要大，这与文献［17］给出的计算结果相似，可能需要采用更合理的材料模型来提高模拟结果的准确性。综合上述计算结果可见，本文的自适应耦合算法和相应的程序是正确可靠的。

3.3 铝板侵彻

考虑直径12.9 mm、长88.9 mm、φ(头部曲率半径与直径之比)为3.0 的卵形4340 钢弹以不同速度正侵彻厚26.3 mm、边长304 mm 的6061-T651 铝板。采用自适应耦合算法和SPH 法对此问题进行对比计算。计算中，弹体视为理想弹塑性体;靶体等效为304 mm 直径的圆靶，采用Johnson-Cook 粘塑性模型和Mie-Grüneisen 状态方程。弹体的材料参数为:ρ=7.83 g/cm3，E=206 GPa，ν=0.3，Y0=1.43 GPa。靶体的材料参数见表1。靶体的基本参数(ρ、E 和ν)取自文献［19］，Johnson-Cook 模型参数A、B 和n 通过最小二乘法拟合实验测得的应力应变曲线［19］得到，其余参数参考文献［20］中相同材料的参数。自适应耦合计算的初始模型由11 444 个三角形单元组成;SPH 计算模型由10 963 个粒子组成，弹/靶接触界面采用粒子-粒子接触算法处理。

表1 靶体材料参数Table 1 Material properties of target

图9 给出了2 种算法计算的5 种不同初始冲击速度vi下弹体的剩余速度vr，并与实验结果［19］进行了对比。自适应耦合算法和SPH 的结果与实验结果都符合较好。在5 种工况下，自适应耦合法与实验结果的平均相对误差为3.4%，SPH 法与实验结果的平均相对误差为2.9%，两者的计算精度接近。

图10 给出了初始冲击速度为508 m/s 工况下2 种算法计算的相同时刻的变形结果(只给出了弹体和靶体中心区域的变形)，2 种算法给出的变形很接近。应用自适应耦合算法时，只有弹/靶接触界面附近的局部区域内的少数单元转化为粒子。在相同的计算条件下，到200 μs 时，自适应耦合算法耗时20 min，SPH 方法耗时71 min，前者的计算效率大大高于后者。对于其他工况，也有相同的结论。

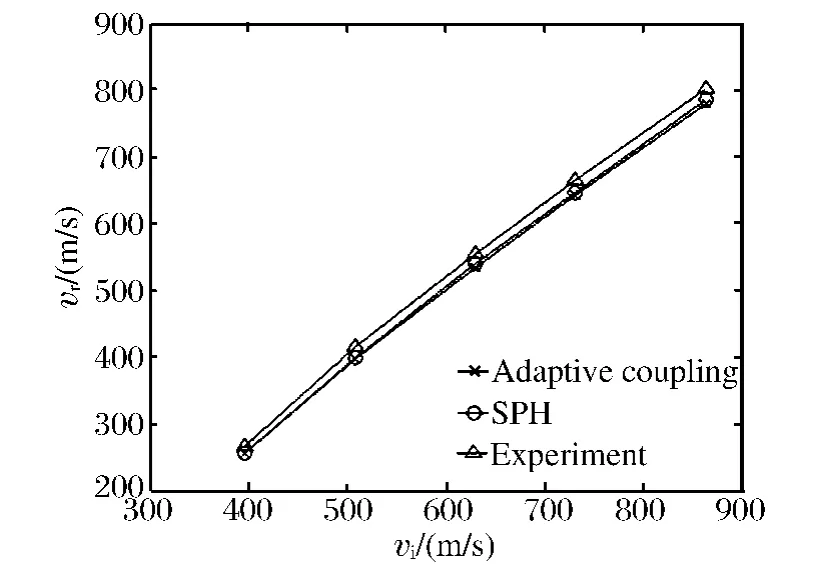
图9 弹体剩余速度的比较Fig.9 Comparison of residual velocities of the projectile

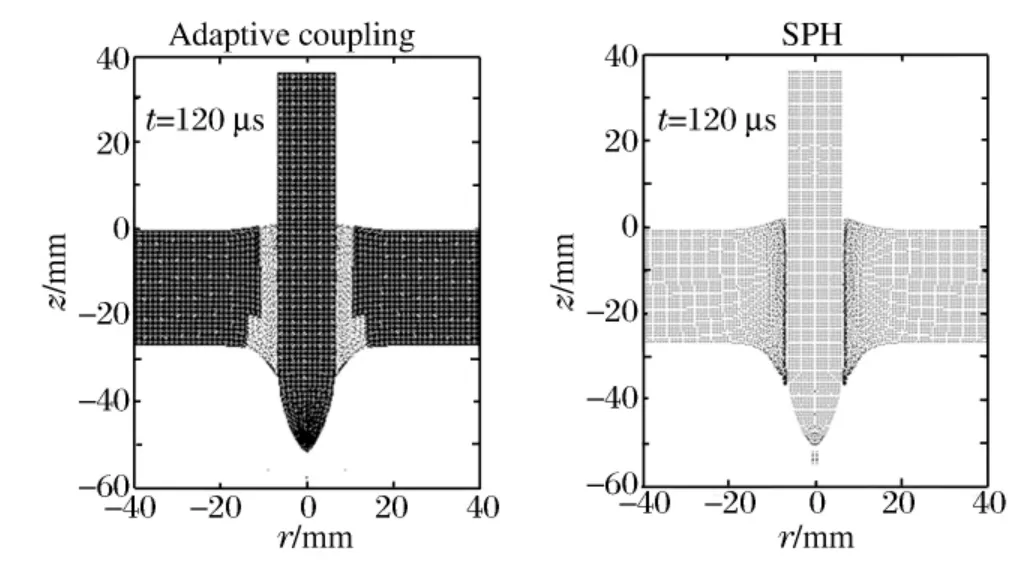
图10 508 m/s 冲击速度下的变形比较Fig.10 Comparison of deformations at impact velocity of 508 m/s

3.4 混凝土侵彻

考虑长143.7 mm、直径25.4 mm、φ=3.0 的卵形弹以606 m/s 的速度正侵彻厚178 mm、抗压强度48 MPa 的混凝土板。采用自适应耦合算法和固定耦合算法进行计算。自适应耦合计算的初始模型采用1 124 个三角形单元离散弹体和33 600 个三角形单元离散靶体，计算过程中将畸变单元转化为粒子。固定耦合计算模型采用1 124 个三角形单元离散弹体和33 600 个粒子离散靶体，计算中无需将单元转化为粒子。弹体考虑为弹塑性等向硬化材料，材料参数为:ρ=8.3 g/cm3，E=200 GPa，ν=0.3，Y0=1.72 GPa，切线模量ET=15 GPa。混凝土材料模型采用HJC 模型，材料参数参考文献［21］。

图11 为弹体的速度时间历程。自适应耦合算法与固定耦合算法的计算结果很接近，计算的剩余速度分别为464 和466 m/s，均与实验结果［22］(449 m/s)符合较好。图12 为2 种方法计算的4 个时刻的变形。在每一变形图中，轴线右边为自适应耦合计算结果，左边为固定耦合计算结果。从图中可以看到，弹体在侵彻过程中变形很小，混凝土靶体被侵彻后发生严重破坏，在弹体入射面和射出面出现材料的飞溅和脱落。这些现象与物理实验中观察到的现象相符。图13 为计算得到的混凝土靶的损伤图像。2 种算法给出的损伤的分布趋势大致相同:在弹体通道的周围形成连续的完全损伤区域;在远离弹体通道处，出现损伤裂纹，并扩展到靶板的边缘。上述结果表明:两种算法均能较好地模拟弹体对混凝土靶的侵彻毁伤过程。从计算效率上看，自适应耦合算法和固定耦合算法分别耗时59 和167 min，前者的计算效率远高于后者。

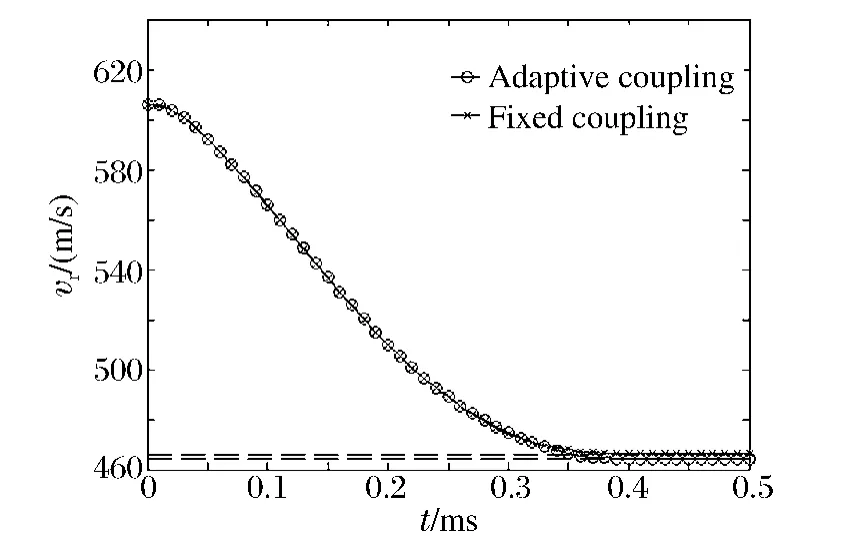
图11 弹体的速度时间历程Fig.11 Velocity histories of the projectile

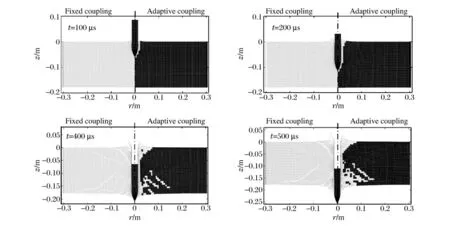
图12 自适应耦合和固定耦合计算的变形比较Fig.12 Comparison of deformations calculated by adaptive and fixed coupling

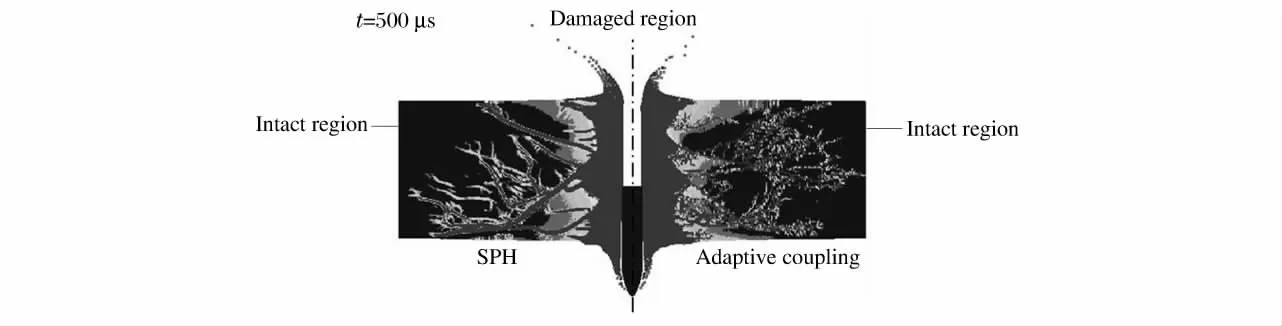
图13 混凝土损伤图像的比较Fig.13 Comparison of the damage of the concrete plate

4 结 论

提出了一种自适应轴对称FEM-SPH 耦合算法并开发了相应的程序。通过对应力波传播和泰勒杆问题的计算验证了算法和程序的正确性，并将该算法应用于弹体侵彻铝板和混凝土板的模拟中，获得了与实验相符的计算结果。提出的自适应算法既克服了单元畸变，又尽可能地减小了SPH 计算区域。它充分利用了FEM 和SPH 各自的优势，计算精度和效率都较好，非常适合于高速冲击问题模拟。另外，本文算法虽是针对二维轴对称问题的，但其具有很好的扩展性，其中涉及的单元-粒子耦合算法、单元向粒子的转化算法等都很容易拓展到三维问题。在后续研究中，将基于本文思想，进一步开发三维自适应FEM-SPH 耦合算法，从而满足更多实际工程问题的模拟需求。

［1］ Lucy L B.A numerical approach to the testing of the fission hypothesis［J］.The Astronomical Journal，1977，82(12):1013-1024.

［2］ Gingold R A，Monaghan J J.Smoothed particle hydrodynamics:Theory and application to non-spherical stars［J］.Monthly Notices of the Royal Astronomical Society，1977，181(2):375-389.

［3］ 武玉玉，何远航，李金柱.耦合方法在超高速碰撞数值模拟中的应用［J］.高压物理学报，2005，19(4):385-389.WU Yu-yu，HE Yuan-hang，LI Jin-zhu.Application of the coupling method in simulating the hypervelocity impact［J］.Chinese Journal of High Pressure Physics，2005，19(4):385-389.

［4］ 王吉，王肖钧，卞梁.光滑粒子法与有限元的耦合算法及其在冲击动力学中的应用［J］.爆炸与冲击，2007，27(6):522-528.WANG Ji，WANG Xiao-jun，BIAN Liang.Linking of smoothed particle hydrodynamics method to standard finite element method and its application in impact dynamics［J］.Explosion and Shock Waves，2007，27(6):522-528.

［5］ 张志春，强洪夫，高巍然.一种光滑粒子流体动力学-有限元法转换算法及其在冲击动力学中的应用［J］.西安交通大学学报，2011，45(1):105-110.ZHANG Zhi-chun，QIANG Hong-fu，GAO Wei-ran.Conversion of 3D distorted finite elements into SPH particles during impact dynamic deformation［J］.Journal of Xi’an Jiaotong University，2011，45(1):105-110.

［6］ Johnson G R.Linking of Lagrangian particle methods to standard finite element methods for high velocity impact simulations［J］.Nuclear Engineering and Design，1994，150(2/3):265-274.

［7］ Attaway S W，Heinstein M W，Swegle JW.Coupling of Smooth particle hydrodynamic with finite element method［J］.Nuclear Engineering and Design，1994，150(2/3):199-205.

［8］ De Vuyst T，Vignjevic R，Campbell J C.Coupling between meshless and finite element methods［J］.International Journal of Impact Engineering，2005，31(8):1054-1064.

［9］ Sauer M.Adaptive kopplung des netzfreien SPH-verfahrens mit finiten elementen zur berechnung von impaktvorg-ängen［D］.Munich:Universität der Bundeswehr München，2000.

［10］ Xiao Y H，Han X，Hu D A.A coupling algorithm of finite element method and smoothed particle hydrodynamics for impact computations［J］.Computers，Materials＆Continua，2011，23(1):9-34.

［11］ Monaghan J J，Lattanzio J C.A refined particle method for astrophysical problems［J］.Astronomy and Astrophysics，1985，149(1):135-143.

［12］ Johnson G R.Artificial viscosity effects for SPH impact computations［J］.International Journal of Impact Engineering，1996，18(5):477-488.

［13］ Johnson G R，Stryk R A，Holmquist T J，et al.Numerical algorithm in a Lagrangian hydrocode［R］.WL-TR-1997-7039.Wright Laboratory，1997.

［14］ Johnson G R，Stryk R A.Symmetric contact and sliding interface algorithms for intense impulsive loading computations［J］.Computer Methods in Applied Mechanics and Engineering，2001(35/36):4531-4549.

［15］ Johnson G R，Stryk R A，Beissel S R，et al.An algorithm to automatically convert distorted finite elements into meshless particles during dynamic deformation［J］.International Journal of Impact Engineering，2002，27(10):997-1013.

［16］ Campbell J C，Vignjevic R，Libersky L D.A contact algorithm for smoothed particle hydrodynamics［J］.Computer Methods in Applied Mechanics and Engineering，2000，184(1):49-65.

［17］ Libersky L D，Petschek A G，Carney T C，et al.High strain Lagrangian hydrodynamics:A three-dimensional SPH code for dynamic material response［J］.Journal of Computational Physics，1993，109(1):67-75.

［18］ Johnson G R，Holmquist T J.Evaluation of cylinder-impact test data for constitutive model constants［J］.Journal of Applied Physics，1988，64(8):3901-3910.

［19］ Piekutowski A J，Forrestal M J，Poormon KL，et al.Perforation of aluminum plates with ogive-nose steel rods at normal and oblique impacts［J］.International Journal of Impact Engineering，1996，18(6):877-887.

［20］ Kmetyk L N，Yarrington P.CTH analyses of steel rod penetration into aluminum and concrete targets with comparison to experiment data［R］.SAND 94-1498.Sandia National Laboratories，1994.

［21］ Holmquist T J，Johnson G R.A computational constitutive model for concrete subjected to large strains，high strain rates and high pressure［C］∥Murphy M J，Backofen J E.14th International Symposium on Ballistics.USA:American Defense Preparedness Association，1993:591-600.

［22］ Hanchak S J，Forrestal M J，Young E R，et a1.Perforation of concrete slabs with 48 MPa and 140 MPa unconfined compressive strengths［J］.International Journal of Impact Engineering，1992，12(1):1-7.