黄土高原降水量空间插值方法研究

赵 婷，杨旭艳

(1.西北大学 城市与环境学院，陕西 西安710127;2.丹凤县气象局，陕西 丹凤726200)

黄土高原地域广阔，水资源时空分布复杂多变，而降雨是地表及地下水资源的主要补给来源，认识降雨时空演变规律对科学利用和调控有限水资源尤为重要。由于气象站点的有限性，定点观测到的降水量数据只能代表该气象站点的降水量，不能直接用于其他地点，更不能代替某一较大面积上的平均值，从而使研究降水量时空分布特征产生了局限性。随着地统计学以及地理信息系统的发展，通过对已知站点降水量数据进行空间插值，实现由点数据到面数据的转化，生成研究区降水量的空间分布图，对研究大面积降水量时空分布特征是一种有效的解1决方法。

近年来，国外对此已进行了大量研究［1－2］，而国内研究还相对较少，尤其是大范围长时间尺度区域的空间插值方法研究。为了探究黄土高原地区最优的降水量空间插值方法，本文利用黄土高原已知的108个气象站点降水量资料，对黄土高原1980－2009年30年的平均降水量进行空间插值精度比较，探讨不同插值方法对研究黄土高原水资源空间分布特征的影响，继而利用最优的插值方法得到黄土高原的空间分布图，为黄土高原的水资源分布状况研究工作起到一定的促进作用。

1 研究区概况及数据来源

1.1 研究区概况

黄土高原，地理范围介于 33°43'－ 41°16'N，100°54'－114°33'E之间，是指北迄阴山，南至秦岭及伏牛山日月山，太行山以西，贺兰山以东，海拔高度为600～2 000 m，是我国的一个重要自然单元。黄土高原包括了宁夏回族自治区全部、甘肃省的陇中和陇东地区、青海省的东北部、内蒙古自治区的河套平原和鄂尔多斯高原、陕西省的中部和北部、河南省的西部丘陵地带等共232个县(市)。东西长约1 300 km，南北宽约 800 km，总面积 62.68万 km2，占全国总面积的6.5%。按中国气候区划，黄土高原可分属四个气候区:盐池—同心—兰州以西及长城以北属于温带干旱气候;宁南、陇中、陕北榆林及晋西北属于温带半干旱气候;陇南、陇东、陕北延安及晋中属于暖温带半干旱气候;南部平原地区属于暖温带半湿润气候［3］。

1.2 数据来源及处理

降水量数据来源于国家气象局1980－2009年共30年的降水观测值［4］。由逐日降水计算多年年均降水，然后在ARCGIS中根据气象站点的地理坐标将各站点降水量转换为.shp文件，以便进行空间插值。为了保证空间插值的边界站点的准确性，特选取黄土高原区域及其向外扩充100 m范围内的气象站点，共108个气象站点，站点分布图如下图所示。同时，为了使插值方法更加准确，根据均匀分布的原则，提取铜川、兰州、会宁、杭锦后旗、三门峡、库泽、定边、海原、凤翔、东胜10个站点的年降水量作为内插检验数据。

2 研究方法

2.1 反距离加权插值法(IDW)

IDW是一种精确插值方法，它假设未知值的点受近距离控制点的影响比远距离控制点的影响更大。将计算区域划分成若干矩形网格，每个网格的宽度和长度分别为Δx和Δy，网格格点处的降水量xj可用其周围邻近的气象站实测资料按距平方的倒数插值求得，即:

式中:x”j为第j个格点处插得的降水量;pi为第j个格点邻近的第i个气象站点的实测降水量;di为第j个格点到其周围邻近的第i个气象站点距离;m为第j个格点邻近的气象站点个数［5，6］。

反距离加权插值的一个重要特征是所有预测值都介于已知的最大值和最小值之间。反距离加权插值法的缺点是其计算值易受数据点集的影响，从而使计算结果常出现一种孤立点数据明显高于周围数据点的情况。

2.2 全局多项式插值(GPI)

全局性插值方面以整个研究区的样点数据集为基础，用一个多项式来计算预测值，即用一个平面或曲面进行全区特征拟合。线性或一阶趋势面用如下方程:

式中，属性值Z是坐标x和y的函数。系数 b由控制点估算［5，6］。

因为趋势面模型的构建方法类似于回归模型的最小二乘法，其拟合程度可用相关系数确定和检验。

2.3 局部多项式插值(LPI)

局部多项式插值采用多个多项式，每个多项式都处在特定重叠的临近区域内。通过使用搜索临近区域对话框定义搜索的临近区域。在局部多项式插值方法中，临近区域的形状、要用到的样点数量的最大值和最小值以及扇区的构造都需要进行设定。还可以通过拖动一个画块改变参数值定义临近区域的宽度。

2.4 径向基函数插值(RBF)

径向基函数插值数据精确插值方法，从概念上来说，相当于将一个软膜插入并经过各个已知样点，同时使总曲率最小。径向基函数包括五种不同的基本函数:平面样条函数、张力样条函数、规则样条函数、高次曲面函数和反高次曲面样条函数。本文以张力样条函数作为主要实验方法。

2.5 克里金插值方法

克里金插值方法是以空间自相关性为基础，利用原始数据和半方差函数的结构性，对区域化变量的未知采样点进行无偏估值的插值方法。克里金法假设某种属性的空间变异性包括三种影响因素:表征区域变量变异的空间相关因素;表征趋势的“漂移”或结构;随机误差。对几种影响的不同解释，形成用于空间插值的不同克里金法。主要包括普通克里金、简单克里金、泛克里金、协同克里金、析取克里金法等。本文以普通克里金法插值为例进行原理讲述。

普通克里金法假设不存在漂移，重点考虑空间相关的因素，并用拟合的半变异直接进行插值。估算某测量点z值的通用方程为:

式中:Z0是待估计值，Zx是已知点x的值，Wx是与已知点关联的权重，s是用于估算的已知点的数目，权重可由对一组联立方程求解得到［5，6］。克里金法中用到的权重不仅与估算点和已知点之间的半变异有关，还与已知点之间的半变异有关。因此，使克里金插值与反距离插值想区别，后者只用已知点和估算点估算权重。

3 插值结果与分析

3.1 不同空间插值方法精度比较

本研究采用反距离加权插值法(IDW)、全局多项式插值法(GPI)、局部多项式插值法(LPI)、径向基函数插值法(RBF)以及克里金(Kiging)方法进行插值，其中克里金插值法分别采用简单插值和普通插值。运用Cross－Validation进行交叉验证以及10个站点的检验数据进行内插检验，对各参数进行修正，以期得到最好的插值结果［9－12］。

将以上插值方法所得拟合值与实测值进行比较，计算误差均值(MEAN)和误差均方根(RMS)，结果如表1。一般来说，各种插值方法的MEAN和RMS总体最小者，具有较好的插值效果，尤其是RMS越小越好。从表1可知，交叉检验和内插检验误差均方根之和排序为普通克里金插值法＜简单克里金插值法＜径向基函数插值法＜反距离加权插值法＜局部多项式插值法＜全局多项式插值法。同时，从误差均值(MEAN)来看，普通克里金和简单克里金插值效果明显优于常规插值方法。从插值的MEAN和RMS总体最小而言，地统计学方法优于常规插值方法，普通克里金和简单克里金相比较而言，普通克里金法优于简单克里金法。

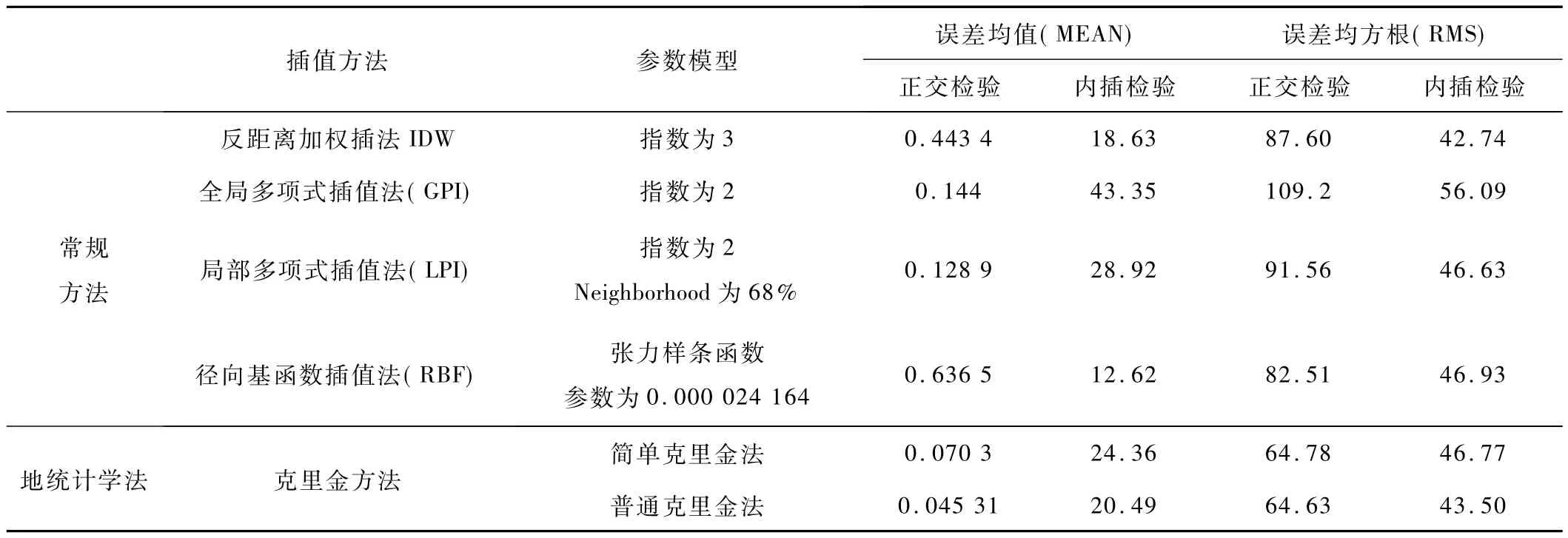
表1 各插值方法误差比较

3.2 黄土高原降水量空间插值结果分析

根据以上分析，采用插值精度最高的普通克里金方法，基于108个气象站对黄土高原降水量进行空间插值，实现点数据到面数据的转换。用黄土高原行政区划图对108个站点30年平均降水量插值得到的栅格图进行截边，得到黄土高原降水量空间分布图。黄土高原年均降水量的空间分布见图2。由图2可知，黄土高原30年平均降水量变化在150～800 mm之间，平均值为400 mm。降水量分布存在明显的地区差异。黄土高原降水量总体分布呈现西北低、东南高的态势，界限很明显。

根据我国对干旱湿润区域的分类标准，对降水量空间插值分布图按照小于200 mm(干旱区)、200～400 mm(半干旱)、400～600 mm(半湿润)、600～800 mm(半湿润)、大于800 mm(湿润)的进行重分类，得到各类的分布面积。在黄土高原，年均降水量小于200 mm的干旱地区占总面积的8.2%，年均降水量为200～400 mm的半干旱地区占总面积的30.3%，年均降水量为400～600 mm的半湿润地区占总面积的50.7%，年均降水量为600～800 mm的半湿润地区占半总面积的10.1%，年均降水量大于800 mm的湿润地区仅占0.7%。黄土高原半湿润和半干旱面积占整个区域面积的4/5以上，因此，黄土高原以半湿润－半干旱气候为主。

4 小结

本文在ARCGIS软件的支持下，用不同的空间插值方法，对黄土高原1980－2009年30年的气象站点的降水量数据进行空间插值，通过对每种插值方法进行正交检验和内插检验，得到各种插值方法的精度排序为普通克里金插值法＜简单克里金插值法＜径向基函数插值法＜反距离加权插值法＜局部多项式插值法＜全局多项式插值法。

选用最优的插值方法普通克里金插值法生成黄土高原降水量空间分布图，分析黄土高原水资源分布状况以及气候。黄土高原的降水量分布呈现出明显的由东南向西北递减的态势，气候也从东南部的半湿润气候转变为半干旱乃至干旱气候。

［1］Mohamed A S.Reliabilty estimation of rainfall－ runoff models［D］.NewYork:State University of New York，1999.

［2］Borga M，Vizzaccaro A.On the interpolation of hydrologic variables:formal equivalence of multiqua－dratic surface fitting and Kriging［J］.J.Hydrol，1997，195(1/4):160 － 171.

［3］刘咏梅.基于高时间分辨率遥感数据的区域水土保持植被综合分类研究—以黄土高原为例［D］.杨凌:中国科学院教育部水土保持与生态环境研究中心.博士论文.2006.

［4］国科学院水利部水土保持研究所.黄土高原水土保持数据库［EB/OL］.［05 －08 － 20］，http://www.loess.csdb.cn/.

［5］Kang－tsung Chang，陈健飞.地理信息系统导论.北京:清华大学出版社.2009.

［6］汤国安，杨昕.地理信息系统空间分析实验教程.北京:科学出版社.2006.

［7］石朋，芮孝芳.降水空间插值方法的比较与改进［J］.河海大学学报:自然科学版.2005，33(4):361－365.

［8］阎洪.薄板光顺样条插值与中国气候空间模拟［J］.地理科学.2004，24(4):163－168.

［9］孟庆香，刘国彬等.黄土高原年均温的空间插值方法研究.干旱区资源与环境.2009，23(3):83 －87.

［10］许家琦，舒红.降水数据空间插值的时间尺度效应［J］.测绘信息与工程.2009，34(3):29 －30.

［11］刘志红，Tim R McVicar，Li Lingtao，等.基于 5变量局部薄盘光滑样条函数的蒸发空间插值［J］.中国水土保持科学.2006，4(6):23－30.

［12］林忠辉，莫兴国，李红轩，等.中国陆地区域气象要素的空间插值［J］.地理学报.2002，57(1):47－56.

［13］蔡福，于慧波，矫玲玲，等.降水要素空间插值精度的比较［J］.资源科学.2006，28(6):73 －79.

［14］万龙，马芹，张建军等.黄土高原降雨量空间插值精度比较——KRIGING与TPS法.中国水土保持科学.2011，9(3):79－87.