伺服机构综合负载模拟试验系统
延皓,李长春,陈策
(北京交通大学 机械与电子控制工程学院,北京100044)
0 引言
为了研制和改进大型运载火箭的伺服机构并对产品进行测试,急需建立一套地面试验系统来复现运载火箭飞行过程中伺服机构的负载情况,包括惯性力矩、弹性力矩、摩擦力矩3 种基本负载,此外还需施加常值力矩来考核系统的某些极限特性。
按照加载方式的不同,负载模拟系统一般分为电动式和电液式。电液式负载模拟系统主要由驱动系统和加载系统两部分组成,前者为位置闭环系统,后者为力闭环系统,它比电动系统有更宽的工作频带和更大的输出力矩[1-2]。针对电液式负载模拟系统,有学者提出综合考虑系统基本性能和用户需求的负载模拟器评价指标体系,以无扰频率特性、多余力、动态跟踪和载荷谱跟踪4 个方面评价负载模拟器[3]。而采用先进控制理论来研制满足需求的电液式负载模拟系统,一直是半实物仿真技术发展的前沿课题,众多学者对此开展了深入研究[4-6]。近年来,研究集中在将反馈控制理论应用到了负载模拟系统中,设计可在线调整的鲁棒控制器,提高加载精度[7-9]。在系统建模方面,有学者考虑了力矩传感器的刚度和摆动马达的转动惯量对系统的影响,建立了某种电液负载模拟系统的精确数学模型,全面描述了系统的动态特性[10]。
有关电液式负载模拟系统的研究主要有以下不足:1)主要用于对弹性负载和常值负载的模拟,对惯性负载及摩擦负载的模拟效果不佳;2)未考虑安装结构柔度对系统特性以及多余力抑制的影响,而这是影响运载火箭伺服机构动态特性的重要因素。
针对上述不足,本文提出了一种能够同时模拟惯性、弹性、摩擦以及常值4 种负载的综合负载模拟系统。
1 工作原理
1.1 总体机械机构
为了模拟伺服机构所受到的惯性、弹性、摩擦、常值等力矩,并复现伺服机构的动态负载特性,设计综合负载模拟系统,主要由被试伺服机构、加载伺服系统、刚度调整装置、线位移传感器、转动横梁、角位移传感器、摩擦力矩加载装置、弹性负载加载装置、惯量调整机构等组成,如图1所示。
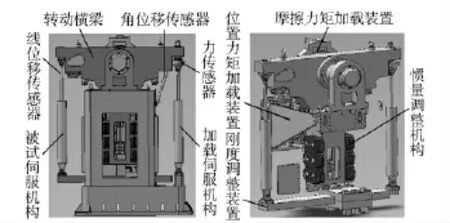
图1 负载模拟器机械结构Fig.1 Mechanical structure of load simulator
1.2 惯量调整机构
惯性负载是负载模拟系统中占有主导地位的负载。采用液压或电动的方式时,微小滞后会给整个系统的负载带来很大影响。在本系统中,通过改变附加质量块的位置和数量,从而达到改变整个系统惯量的目的。如图2所示为惯量调整机构原理图。
1.3 弹性负载加载装置
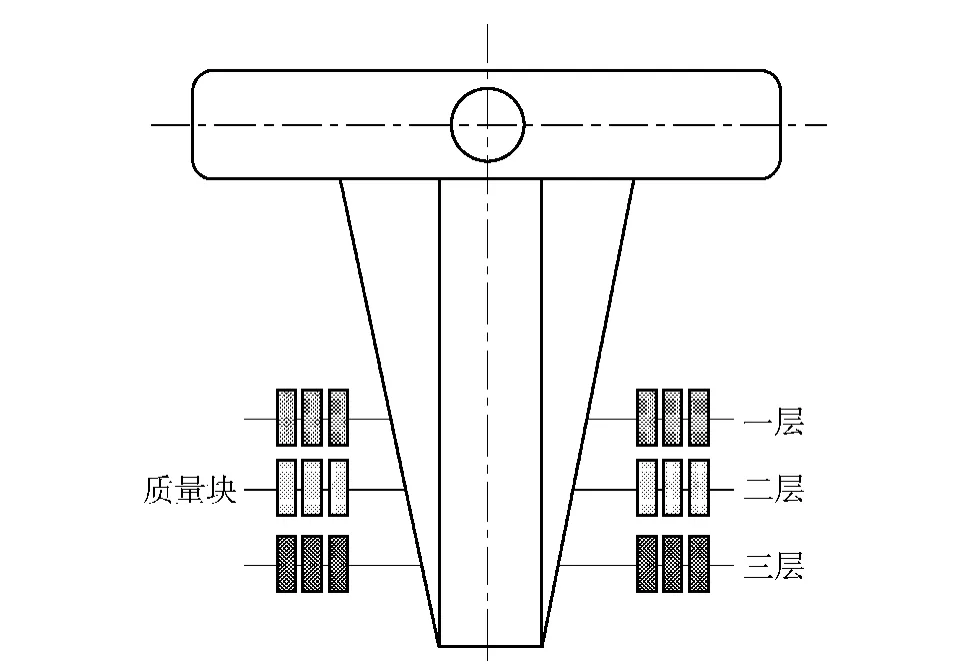
图2 惯量调整机构原理图Fig.2 Inertia adjusting mechanism
在转动横梁绕转轴摆动过程中,使得弹性调节板发生弹性形变,实现弹性负载的加载,并通过弹性调节板跨度的连续变化来实现弹性负载的连续调节。为了降低刚度以适应弹性负载加载的需要,将弹性调节板设计成梯形。如图3所示为弹性负载加载装置原理图。
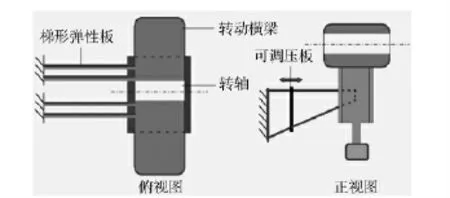
图3 弹性负载加载装置原理图Fig.3 Elastic loading device
将梯形弹性板按跨度L 方向等分为N 个微元,每段微元长度为Δx,如图4所示。通过设置铰链、轴套和导轨,使得弹性板只在端部承受垂直于板面的力,不受扭矩及其他方向的力。
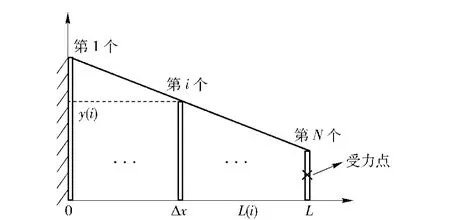
图4 梯形弹性板原理图Fig.4 Trapezoidal elastic plate
第i 个微元截面处对应的弯矩为
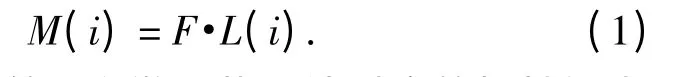
梯形弹性板第i 个微元截面处对应的惯性矩为
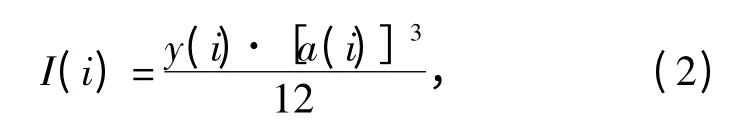
式中:a(i)为弹性板每一截面处对应的厚度。
梯形弹性板第i 个微元截面处对应的相对转角为
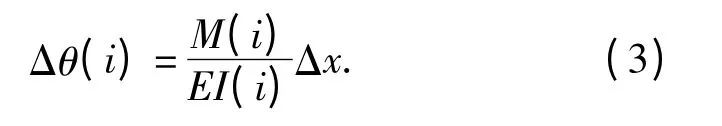
梯形弹性板第i 个微元截面处的相对转角与前一个微元截面处相对转角之间的关系为

梯形弹性板挠度变化公式为:
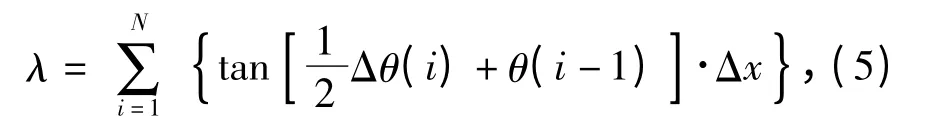
则弹性板刚度为

式中:l 为弹性板受力点相对转动横梁回转中心的力臂。
1.4 刚度调整装置
在负载模拟系统中利用被试伺服机构连接弹性支撑板来模拟安装结构柔度。在转动横梁摆动过程中,刚度支撑板发生弹性形变,支撑刚度的大小通过调整弹性支座和刚度支撑板之间的距离来改变,并通过改变双层压板的固定位置来实现支撑刚度的连续调节。如图5所示为刚度调整装置的原理图。
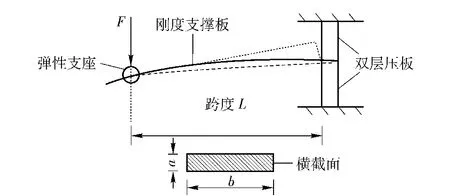
图5 刚度调整装置原理图Fig.5 Stiffness adjusting device
弹性支撑板的挠度为

则弹性支撑板的刚度为
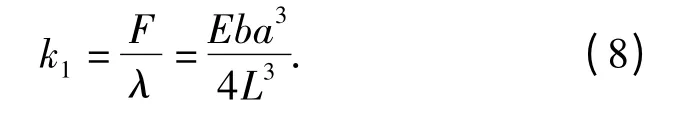
1.5 摩擦力矩加载装置
摩擦负载加载方式采用4 个差动液压缸对摩擦片施力,通过摩擦片与摩擦盘发生干摩擦产生摩擦力矩,以实现对负载的摩擦阻力的模拟。该方法实现了较大可控摩擦力的加载,使得摩擦力矩的加载不会产生滞后,与实际摩擦力矩相一致。如图6所示为摩擦力矩加载装置原理图。
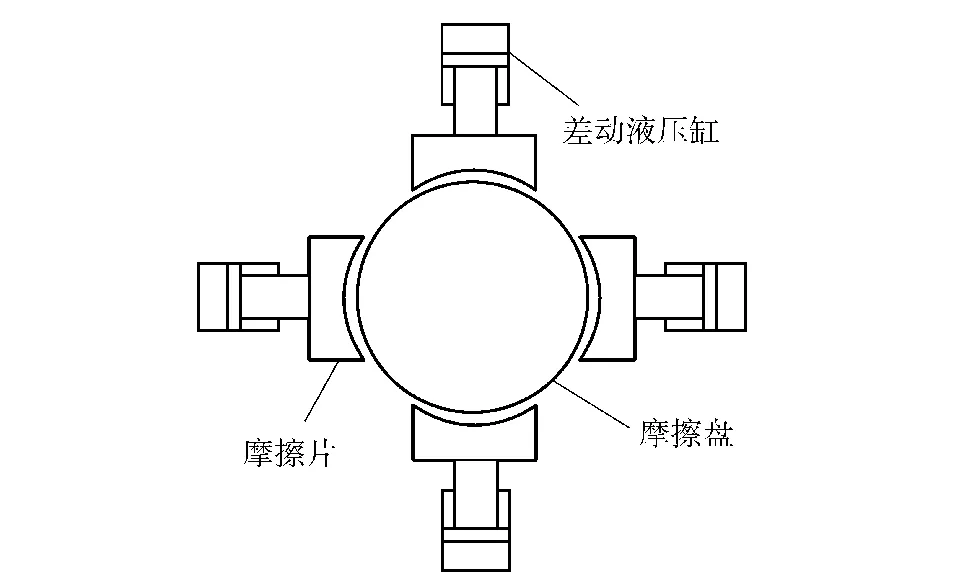
图6 摩擦力矩加载装置原理图Fig.6 Friction torque loading device
2 伺服机构动态特性分析
根据负载模拟系统的结构原理,在不考虑加载伺服系统的情况下,负载模拟系统应能实现对伺服机构动态特性的模拟。在伺服机构的设计和研制过程中,其动态特性是由所谓的角位移与线位移随振动频率变化时的关系来描述。角位移指的是火箭发动机的偏转角度,线位移指的是伺服机构作动筒活塞相对于缸筒的位移。对于火箭发动机实体,角位移相对线位移的频率特性在某些频率点上出现谐振峰,在高频段快速衰减。谐振峰与安装结构柔度、发动机的转动惯量等有关。如图7所示,描述了系统模拟伺服机构动态特性的工作原理。
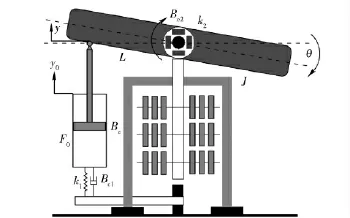
图7 动态特性模拟的物理模型Fig.7 Physical model of dynamic characteristic
根据图7所示的物理模型,建立系统数学模型。
1)由于缸筒连接在弹性板上,运动过程中不能将其视为静止的,所以需要考虑缸筒的动力学特性。建立液压缸筒的受力平衡方程:
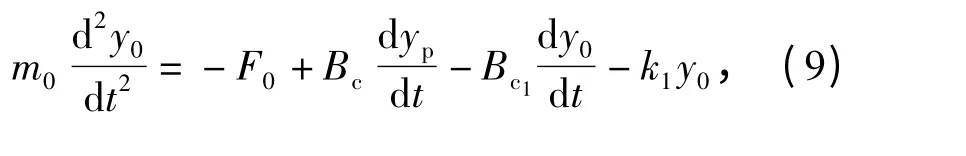
式中:m0为液压缸筒的质量;y0为液压缸筒的绝对位移;F0为液压缸对活塞杆的驱动力;Bc为液压缸的粘性阻尼系数;yp为活塞杆的相对位移;Bc1为液压缸筒与弹性板之间的阻尼系数;k1为液压缸筒与弹性板之间的支撑刚度。
2)伺服机构的连续性方程:
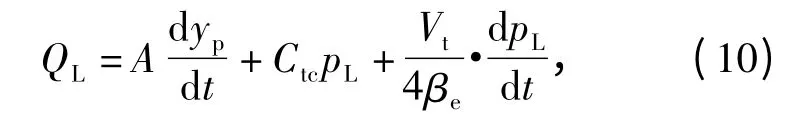
式中:A 为活塞有效面积;Ctc为泄漏系数;Vt为油腔总容积;βe为等效体积弹性模数。
3)伺服阀的流量方程:
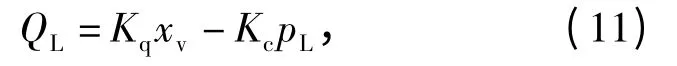
式中:QL为负载流量;Kq为流量增益;Kc为流量-压力系数;xv为阀芯位移;pL为负载压力。
4)转动横梁的受力平衡方程:
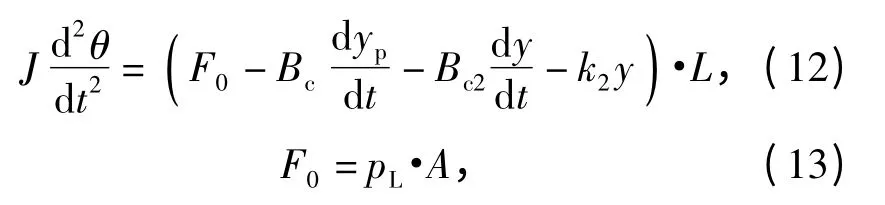
式中:J 为系统转动惯量;θ 为转动横梁的转角;Bc2为摩擦负载下的阻尼系数;k2为弹性负载下的弹性刚度;y 为转动横梁的垂向绝对位移;L 为转动横梁总长度的1/2.
5)伺服机构的位移平衡方程:

对上述方程(9)~(15)进行拉式变换:
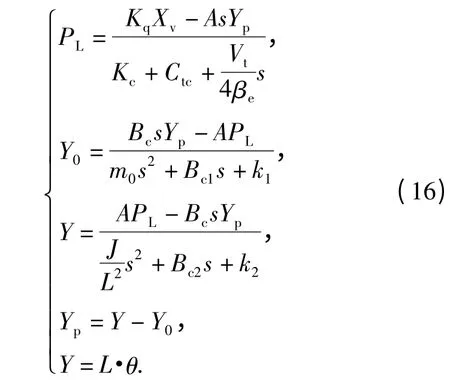
建立系统开环传递函数模型如图8所示。
可以看出,与一般的传递函数模型相比,在考虑安装结构柔度后,所建立的系统模型中增加了缸筒动力学环节,其中包含了安装基础的刚度,它对系统的动态特性有较大影响。
根据图8建立闭环控制系统,对伺服机构的动态特性进行仿真。主要仿真参数如下:A =0.005 9 m2,βe=6.9 ×108Pa,Vt=0.001 2 m3,Kce= Kc+ Ctc=4 ×10-11m3·s-1/Pa.仿真结果如图9所示。
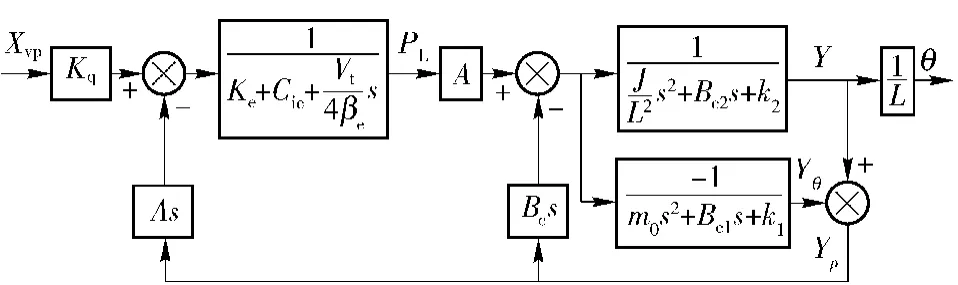
图8 系统开环传递函数模型Fig.8 Open-loop transfer function model of the system
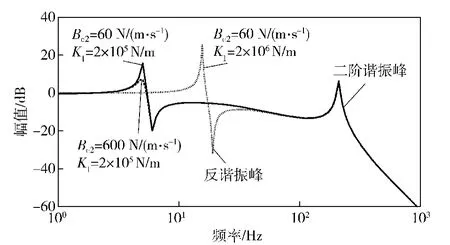
图9 谐振仿真Bode 图Fig.9 Bode diagram of resonant simulation
仿真曲线中出现两个谐振峰:第1 个谐振峰是由安装结构柔度和负载惯量构成的质量弹簧系统引起;第2 个谐振峰的出现是由于考虑了缸筒质量。仿真结果表明,负载模拟系统能够实现伺服机构动态特性中的谐振峰,通过调节阻尼系数可改变谐振峰幅值,通过调节安装结构柔度可以改变谐振峰频率,同时谐振峰峰值也发生改变。而在此过程中,二阶谐振峰保持不变。
3 综合系统模型
根据负载模拟系统的结构原理,考虑加载系统与被试伺服机构之间的耦合,并对系统进行简化成平动系统,得到综合系统物理模型[11-12]如图10 所示。
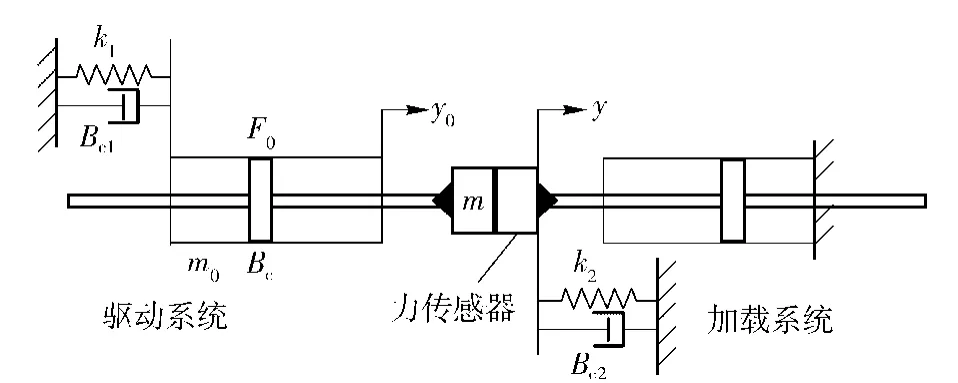
图10 综合系统物理模型Fig.10 Physical model of the comprehensive system
于是,将图8中被试伺服机构的传递函数模型与电液力控制系统模型相耦合,得到综合负载模拟系统数学模型,作为仿真研究基础以及实验参数调 整的依据,如图11 所示。
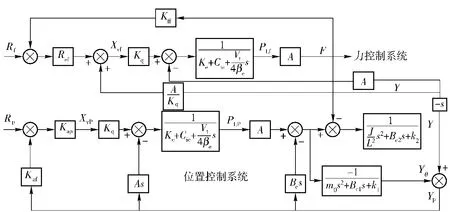
图11 综合系统数学模型Fig.11 Mathematical model of the comprehensive system
与安装柔性结构相比,驱动系统与加载系统活塞杆之间的连接刚度以及力传感器的刚度较大,在模型中将其视为一体,因此为了抑制加载系统的多余力,前馈采用的速度为活塞杆运动的绝对速度,这一点与一般加载系统的等效负载模型有所不同。
根据图11 中的数学模型,对综合负载模拟系统进行仿真,仿真结果如图12 所示。虽然与一般的负载模拟系统结构上有所差别,但伺服机构依然有着很好的跟踪性能。该系统也存在多余力,仿真中采用与一般系统相同的方法,根据结构不变性原理进行前馈补偿,可以完全消除多余力,证明了综合负载模拟系统的结构设计是可行的。
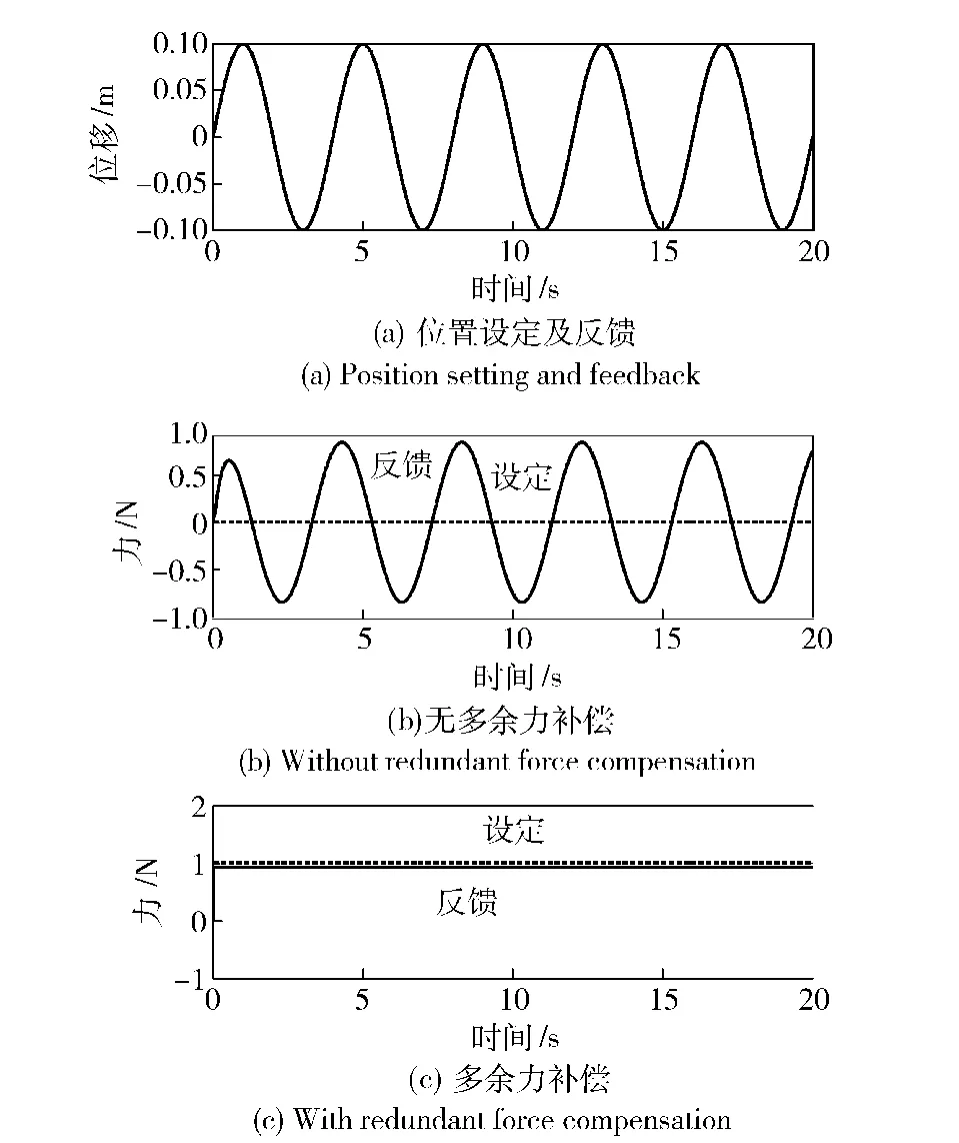
图12 系统仿真结果Fig.12 Results of system simulation
4 实验研究
4.1 基本实验参数测试结果
根据上述设计和分析,构建运载火箭综合负载模拟系统,如图1所示。对系统的基本参数进行测试,结果如表1所示。

表1 基本参数测试结果Tab.1 Results of basic parameter test
4.2 综合负载模拟系统实验研究
以综合负载模拟系统为研究平台,并以被试伺服机构中的线位移作为输入,以转动横梁的角位移作为输出,通过实验绘制系统Bode 图,如图13 所示。可看出系统成功实现了对伺服机构一阶谐振的模拟,与仿真结果一致。实验中由于采用的阀控缸系统性能低于真实的伺服机构,因此无法在更高的频率段进行测试。
采用加载系统模拟伺服机构受到的常值负载,给伺服机构一个正弦输入信号,伺服机构能够进行很好的位置跟踪,但加载系统有着较大的多余力。根据前面分析,多余力的消除需要已知转动横梁的角速度,而目前实验条件下只有角位移传感器。然而伺服机构的动态实验一般用正弦信号进行测试,而且频率是已知的,当忽略系统的非线性因素时,转动横梁的转动也是正弦变化的,且频率与输入信号一致,这时可以通过最小二乘方法辨识位置反馈信号的相位,在此基础上重构加载液压缸的速度曲线以抑制多余力,力系统采用比例控制策略。实验曲线如图14 所示,在正弦运动时加载的多余力抑制效果良好。
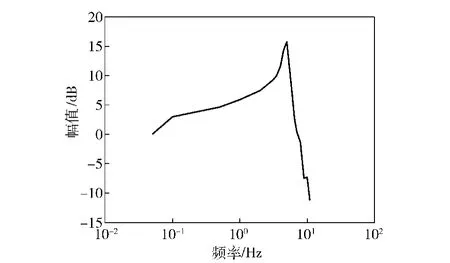
图13 系统Bode 图Fig.13 Bode diagram of the system
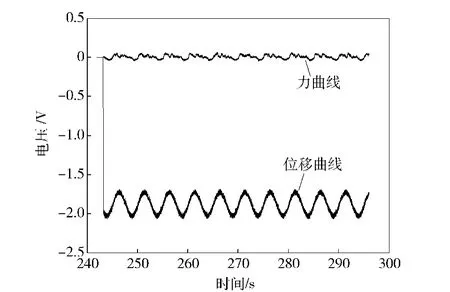
图14 多余力抑制实验结果Fig.14 Experimental results of redundant force compensation
4 结论
1)提出了用于测试伺服机构动态特性的综合负载模拟系统,能够实现对惯性、弹性、摩擦以及常值4 种负载单独或同时模拟。由于惯性负载和弹性负载也采用机械结构来实现,有效地降低了加载液压系统任务的复杂性,提高了负载模拟的精确性。
2)由于考虑安装结构柔度,负载模拟系统有着更为复杂的数学模型,必须考虑伺服机构缸筒的动力学特性。因此,系统的负载特性会产生两个谐振峰,且安装基础的刚度将直接影响一阶谐振峰的频率和幅值。
3)与安装基础的刚度相比,伺服机构与加载系统之间的连接刚度要大得多,因此加载系统的模型与一般系统相比是有所不同的。此时需要把活塞杆的绝对速度作为多余力抑制的参考速度,依然可以取得良好的加载效果。
References)
[1] 方强.被动式力矩伺服控制系统设计方法及应用研究[D].哈尔滨:哈尔滨工业大学,2006.FANG Qiang.Research of design method for passive torque servo control system and its application[D].Harbin:Harbin Institute of Technology,2006.(in Chinese)
[2] 刘晓东.电液伺服系统多余力补偿及数字控制策略研究[D].北京:北京交通大学,2008.LIU Xiao-dong.Study on extraneous force compensation and digital control algorithm of electro-hydraulic servo system[D].Beijing:Beijing Jiaotong University,2008.(in Chinese)
[3] 焦宗夏,华清,王晓东,等.负载模拟器的评价指标体系[J].机械工程学报,2002,38(11):26-30.JIAO Zong-xia,HUA Qing,WANG Xiao-dong,et al.Estimation for performance of load simulator[J].Chinese Journal of Mechanical Engineering,2002,38(11):26-30.(in Chinese)
[4] Kyoung Kwan AHN.Self tuning fuzzy PID control for hydraulic load simulator[C]∥International Conference on Control,Automation and Systems.Korea:IEEE,2007:345-349.
[5] Ohuchi H,Jukui H,Inatomi K,et al.Model reference adaptive control of a hydraulic load simulator[C]∥The 3rd International Conference on Fluid Power Transmission and Control.Hangzhou:International Academic Publishers,1993:275-280.
[6] 张彪,赵克定,孙丰迎.电液负载模拟器的神经网络参数辨识[J].航空学报,2009,30(2):374-379.ZHANG Biao,ZHAO Ke-ding,SUN Feng-ying.Neural network parameter identification of electro-hydraulic load simulator[J].Acta Aeronautica et Astronautica Sinca,2009,30(2):374-379.(in Chinese)
[7] Dinh Quang Truong.A study on force control of electric-hydraulic load simulator using an online tuning quantitative feedback theory[C]∥International Conference on Control,Automation and Systems.Korea:IEEE,2008:2622-2627.
[8] Wang J F.Application of H∞control based on mixed sensitivity in the electro-hydraulic load simulator[C]∥International Conference on Mechatronics and Automation.Harbin:IEEE,2007:2991-2996.
[9] Niksefat N.Design and experimental evaluation of a robust force controller for an electro-hydraulic actuatorvia quantitative feedback theory[J].Control Engineering Practice,2000,8:1335-1345.
[10] 华清,焦宗夏,王晓东,等.电液负载模拟器的精确数学模型[J].机械工程学报,2002,38(11):31-35.HUA Qing,JIAO Zong-xia,WANG Xiao-dong,et al.Complex mathematical model of electro-hydraulic torque load simulator[J].Chinese Journal of Mechanical Engineering,2002,38(11):31-35.(in Chinese)
[11] 李洪人.液压控制系统[M].北京:国防工业出版社,1990:314-326.LI Hong-ren.Hydraulic control system[M].Beijing:National Defense Industry Press,1990:314-326.(in Chinese)
[12] 刘长年.液压伺服系统的分析与设计[M].北京:科学出版社,1985:78-134.LIU Chang-nian.Analysis and design of the hydraulic servo system[M].Beijing:Science Press,1985:78-134.(in Chinese)

