谈零件工序尺寸公差的零值和负值
樊 琳
(苏州大学机电工程学院,江苏 苏州 215021)
在生产中,编制零件工艺规程,一般都要涉及工艺尺寸链的计算,特别是遇到零件的工序基准和定位基准(或测量基准)不重合时,计算工序尺寸的公差就会经常出现零值或负值问题。近几年,经过工科教学课程体系改革,相关课程内容合并、压缩和简化,涉及这一部分的知识,在教材中已经不再阐述或仅简单提示一下。当前,由于大学生接触生产实际时间有限,对工序尺寸公差的零值或负值的后果不够清晰以及对解决方法的不了解。为此,笔者根据多年的教学经验,从培养工科大学生应用型的人才出发,认为《机械制造技术》课程的课堂教学可以适当安排一定课时来讲解工序尺寸公差的零值或负值问题。
1 尺寸公差零值或负值的概念
零件尺寸公差是指允许尺寸的变动量。公差等于最大极限尺寸与最小极限之代数差的绝对值,也等于上偏差与下偏差的代数差的绝对值。在计算尺寸链时,工序尺寸的公差值,首先必须是正的,其次公差要有一定范围,公差数值的大小取决产品的性能和使用要求。
在工序尺寸的计算中,当工序基准和定位基准重合时,零件的工序尺寸一般无需计算,也不会出现尺寸公差零值或负值。当工序基准和定位基准不重合时,工序尺寸的计算有可能会出现公差零值或负值。由于尺寸公差的零值和负值会造成零件无法加工,生产中碰到此类问题的一般三种解决方法。
(1)等公差值法
按等公差值方法重新分配封闭环的公差,即:
各组成环公差=封闭环公差/(n-1)
这种方法在计算上比较方便,但从加工工艺上看不够合理,只宜有选择地使用。
(2)等公差级法
按等公差级方法分配封闭环的公差,即各组成环的公差根据其基本尺寸的大小按比例分配,或是按照公差表中的尺寸分段及某一公差等级来规定组成环的公差,使各组成环的公差满足以下条件:
封闭环公差=各组成环公差之和
最后进行适当调整。这种方法从工艺上讲比较合理。
(3)经验法
各组成环的公差可以凭工程技术人员的经验,按照具体情况来分配。
前二种方法都有优点和不足,而经验法对大学生还谈不上。为此,在教学中可以结合生产实际介绍一种既方便又比较合理的方法,即先用等公差值分配公差,再根据尺寸大小适当调整来求解工序尺寸和公差。
2 计算实例
对工序尺寸公差零值和负值的问题,在教学中,还可以通过实例提高学生的认识。
2.1 应用实例
采用调整法铣削,图1所示为阶梯轴的槽面。试标注以大端端面轴向定位时的铣槽工序尺寸及其公差。

图1 零件图
2.2 应用求解
计算该工序尺寸步骤可分三步:
(1)画尺寸链图,见图2。
(2)确定封闭环及各组成环性质。
封闭环:82±0.5
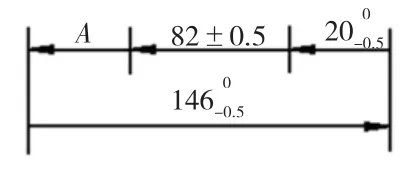
图2 尺寸链
(3)计算工序尺寸和公差
由于在尺寸链计算中,封闭环公差必须大于或等于组成环公差。从以上数值可以看出,封闭环公差为1,已知组成环146和20的公差和也为1,计算工序尺寸A的公差结果为零,需要重新调整组成环公差。
先按等公差值分配组成环公差,即:
各组成环公差=1/(4-1)=0.33
基本尺寸82=146-(A+20)
得A=44
上偏差-0.5=-0.4-(ESA+0)
得ESA=+0.1
下偏差 +0.5=0-(EIA-0.3)
得EIA=-0.2

图3 工序图
3 结束语
工序尺寸公差的零值或负值是零件加工过程中会碰到的实际问题,提出课堂教学增加其内容出于以下几点考虑:
(1)《机械制造技术》课程作为一门机械专业的主干课程,其特点课程的综合应用性高,实践性强。课程内容应该考虑实用性,多讲解一些学生毕业以后马上可以在工作中用到的知识,为学生今后工作打基础。
(2)大学生在校四年虽然学习了许多基础知识和专业理论知识,但还缺乏实践经验。刚到工作单位一般不会搞产品设计,主要做一些如编制零件工艺规程、设计零件专用夹具等工作,多讲一些实用性基础知识对学生今后工作有利。
(3)在课堂教学时数不会增加很多,一般也可以控制在1~2学时内。
另外,实例中零件的径向尺寸没有标出是为了方便讲解,有利学生了解和熟悉工序尺寸中零公差或负公差的知识。

