独立型风光互补系统中储能容量优化研究

何勇琪，张建成

(华北电力大学 电气与电子工程学院，河北 保定071003)

0 引言

随着世界经济的发展，人类对能源的需求量与日俱增，传统的非可再生的石化能源的储量已经急剧下降，在不久的将来这些石化能源将会消失殆尽。所以人类在对能源的寻求上转向了诸多新型可再生能源，诸如风能、太阳能、地热能、潮汐能等，以解决当前的能源紧缺问题［1］。偏远地区无法与电网连接，结合当地的自然资源，发展相应的新能源技术，解决当地电力需求是非常必要的。而电网的发展趋势将由以前的大而集中供电转变为小而分散供电。这样能提高电网的安全性，减小由局部故障引发大面积停电的危险。所以，微电网将是现代电力系统的重要发展方向［2，3］。现在开发技术较为成熟的两种新能源为风能和太阳能，而风能和太阳能在时间空间上又具有较好的互补性，再由储能系统来填补气象的随机变化，风光互补发电系统将有很大的发展潜力，目前已有诸多学者从事这方面的研究。文献［4］研究基于遗传算法的风光互补供电系统优化设计，但缺乏对储能装置内在特性的考虑，并且遗传算法要进行复杂的遗传变异操作。而现在针对于风电、光伏的出力预测的研究也在较广泛地进行当中，对风电、光伏进行系统全面的发电预测，预测结果较为准确。文献［4 ～6］研究风光互补优化设计的文章中，在储能容量的优化上只是从其输出电量方面考虑，缺少储能系统功率输出能力方面的考虑。本文将以风电、光伏系统全面的发电预测数据为依托，从储能系统电量输出和功率输出两方面出发，充分考虑储能器件的内部特性来较准确地计算出满足用户所供电要求的储能系统的容量。

1 风光互补发电系统简介

我国目前已有一些风电、光伏发电的示范工程项目，但系统的装机容量较小。随着风电单机容量的提高，光伏技术的进步，以及储能技术的发展，大容量的风电、光伏发电并网项目也会在不久的将来大力发展。而当前国家正在建设较大规模的风光互补发电示范工程也标示着风电、光伏的发展方向。这些示范工程的建设与运行，也为将来风电、光伏发电大规模并网运行积累经验及技术。独立型风光互补发电系统结构如图1。

图1 独立型风光互补发电系统结构图Fig．1 Structure of stand along wind/PV/storage hybrid generation system

独立型风光互补发电系统作为一个优良的分布式电源，在边远山区、高原、海岛等地作为供电电源，充分利用风能和太阳能，对当地负荷进行供电，而它的独立运行也为将来风电、光伏大规模并网运行提供一定的经验。

2 基于粒子群算法的储能容量优化配置

蓄电池作为一个比较成熟的储能器件，具有能量密度高的优点，但同时也具有功率密度低、循环寿命短、充放电效率较小的缺点。超级电容器作为一个新型的储能设备，具有功率密度高、寿命长、充放电速率快等优点，然而与蓄电池相对的是超级电容器的能量密度低，一般只有蓄电池的20%［7］。所以，将超级电容器与蓄电池混合储能，就能将二者的优点相结合，并且通过适当的控制策略，超级电容器能延长蓄电池的使用寿命［8］。超级电容器与蓄电池混合的储能装置能在风光互补发电系统中较好地满足负荷的功率和能量需求。

2.1 优化目标模型

独立型风光互补发电系统储能系统容量优化配置要求在给负荷供电满足一定的要求下，配置储能的费用最小。而给负荷供电的水平由负荷年总缺电率LPSP 来衡量［9］，要求负荷年总缺电率小于制定的标准值，并且储能还应满足支撑负荷的瞬时功率缺失。超级电容器和蓄电池混合储能系统容量优化计算的数学模型为

式中:n1，n2分别为超级电容器和蓄电池的个数;c1，c2分别为超级电容器和蓄电池的单价;Cmax为系统允许的最大储能容量;ΔP 为负荷缺失的功率。

为了精确配置储能装置的容量，要求准确计算负荷缺电率LPSP，然而风、光、负荷的预测数据的准确度和储能装置的内部特性与负荷缺电率LPSP 有着紧密联系。因此，在风光互补发电系统储能容量的最优化中，提高预测数据精确度和考虑储能装置的充放电特性等诸多因素成为必然。

2.2 优化计算方法

2.2.1 负荷缺电率LPSP 的计算

利用风电、光伏以及负荷的发用电预测数据，风电、光伏在给负荷供电时，负荷与风光的求供电差值如下式:

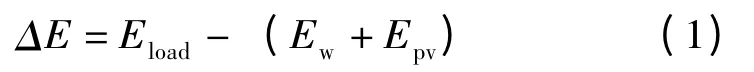
当ΔE≤0 时，说明风电、光伏所发的电量能供应负荷所需，储能装置可以进行充电。

当ΔE ＞0 时，说明风电、光伏所发的电量不能满足负荷的需求，储能装置需要给负荷供电，储能装置放电。为了防止负荷用电时突然的大功率缺失，引起电能质量骤降，给整个发电系统及用户带来损害，储能装置必须能快速输出大功率以支撑系统。超级电容器和蓄电池的联合储能装置发出的总功率必须不小于最大瞬时功率缺失(单位时间内的平均功率)，即

其中［10］:

所以，式(2)变为

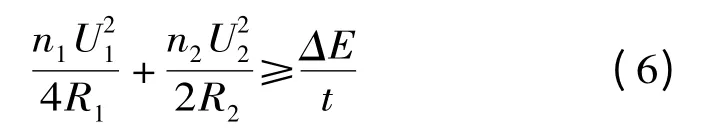
在储能装置能够保证足够的输出功率下，能量输出量也应能达到负荷需求。本文以负荷缺电率来衡量风光互补发电系统的供电效果，所谓负荷的缺电率就是在系统运行过程中，负荷对电能的需求量对所得电量之间的差值(LPS)与负荷总需求量的比值，满足下式［9］:

式中:t 为单位时间间隔;T 为总计算次数。

这时，储能装置里储存的电能与负荷、风光的求供电缺额的差值为

当ΔΔE (t)≥0 时，说明储能装置当时所储存的电量可以填补负荷的需求差值，这时LPS(t) =0。

当ΔΔE (t) ＜0 时，说明储能装置的电量不够填补负荷需求，储能装置差多少电就表明负荷缺多少电，这时缺电量LPS (t) =ΔΔE。

在计算负荷总缺电率时，除了储能容量大小因素，还要估算超级电容器的实际存储的能量和蓄电池的荷电状态，这样才能更加准确地计算负荷缺电率LPSP。通常利用安时计量法来估算蓄电池的荷电状态SOC，如下式［11］:

式中:ηC为充电效率;ηD为放电效率;Iin为充电电流;Iout为放电电流。

虽然在单位计算时间内，储能装置可能会有多次的充放电循环，只要单位计算时间间隔的越小，风电、光伏的发电预测数据与实际数据的误差越小，在单位时间内它们的荷电状态可以用平均量来求某一单位时间开始到下一单位时间开始这段时间内的荷电状态的变化。在风、光、负荷预测数据的每一个单位计算时间内，超级电容器下一时刻存储的能量和蓄电池下一时刻的荷电状态分别为

其中:

由此连续计算，最后得出负荷全年的缺点率LPSP。

2.2.2 粒子群算法

粒子群算法 (Partical Swarm Optimization，PSO)是从随机解出发，通过迭代寻找最优解，它也是通过适应度来评价解的品质，粒子群算法容易实现、精度高、收敛快，没有类似遗传算法的遗传变异等复杂操作。

在每一次迭代中，粒子群里的每一个粒子通过跟踪两个“极值”来更新自己，第一个就是粒子本身所找到的最优解，叫个体极值点pbest;另一个是整个种群目前找到的最优解，叫全局极值点gbest。假设一个由M 个粒子组成的群体在D 维的搜索空间里飞行搜索，粒子i 在t 时刻的状态属性如下:

粒子个体最优位置:

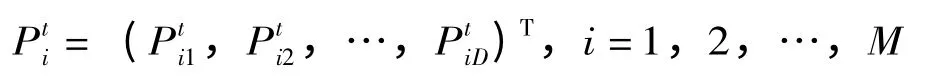
全局最优位置:

粒子在t+1 时刻的位置通过下式更新:

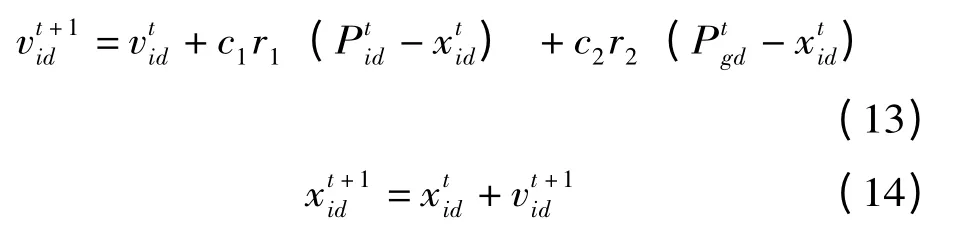
式中:c1，c2为学习因子;r1，r2为两个0 到1 之间的随机数。

这样，粒子位置的每一次变更，计算的值都跟个体最优和全局最优进行比较，粒子的当前值优于个体最优时个体最优被粒子当前值替换，若也优于全局最优值，全局最优也被粒子当前值更替。

所以，基于粒子群的容量优化配置流程如下:

(1)初始化粒子群，在储能容量的取值范围内，每个粒子随机取值，以及初始化个体最优，全局最优。

(3)每个粒子计算储能装置所能发出的最大功率以及相对应的负荷缺电率，是否满足负荷的功率需求以及LPSP (t)≤LPSPmax，若满足，则计算目标函数F (，)，并且与粒子的个体最优、全局最优进行比较，更替最优值。

3 算例分析

假设某一风光互补示范工程规模为100 MW的风电场，50 MW 的光伏发电站，现假设当地负荷为60 MW，并且独立运行，现在要为其配置储能容量。选取的超级电容器的组合单体容量为30 000 F，额定电压为27 V，最大电流为4 500 A，内阻为3 mΩ，单价为10 000 元;选取的蓄电池为铅酸蓄电池，单个铅酸蓄电池的容量为400 Ah，额定电压为24 V，内阻为68 mΩ 蓄电池的最大放电深度为75%，蓄电池单价为2 800 元。

现有预测精度为0.5 h 的风电年发电预测数据、光伏年发电预测数据、负荷年用电预测数据如图2 ～4 所示。

现制定负荷最大缺电率为0.05，在这一水平下，先观察在不考虑储能系统功率输出能力的情况下，储能系统容量的大小和实际供电情况。其结果如表1。

图2 风电0.5 h 发电预测值Fig．2 Forecast of half an hour of wind power

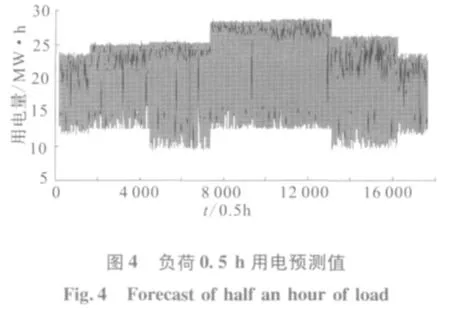
表1 不考虑储能系统输出功率的结果Tab．1 Result of calculation without regard to the power of the storage

由表1 可知，若不考虑储能系统的输出功率能力，满足负荷最大缺电率为0.05 时只需要1 468个蓄电池就足够了，但是由预测数据计算得出负荷的最大瞬时功率缺失为52 890 000 W，而由蓄电池能提供的功率为6 217 411 W，所以这种情况下的储能容量无法满足负载的功率缺额。

在上述同样的供电要求下，现观察考虑储能系统功率输出能力的3 种储能方式来比较它们的容量大小，如表2 所示。

结果表明，由于超级电容器的能量密度低，蓄电池的功率密度低，造成它们储能时在同等供电要求下所需要的成本要比超级电容器和蓄电池混合储能的成本高得多。所以，利用超级电容器和蓄电池的混合储能系统能提高经济效益。

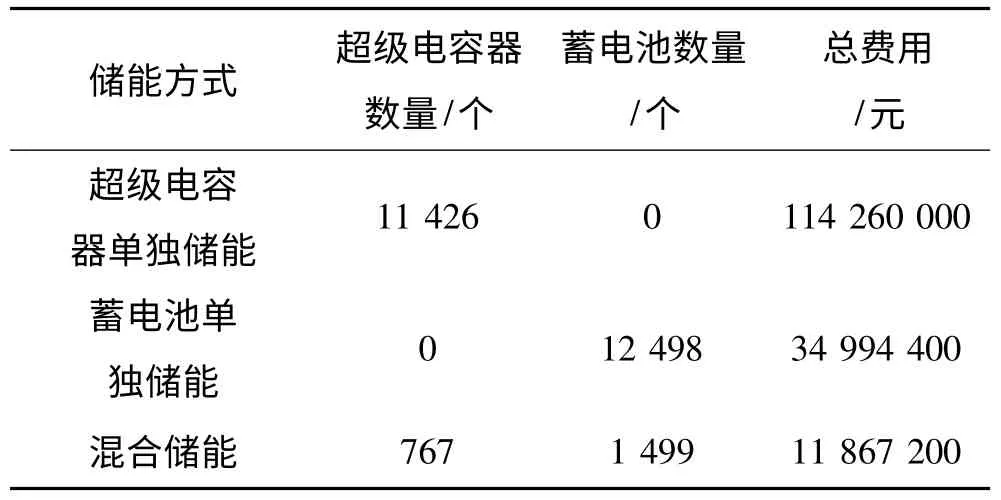
表2 3 种储能方式结果Tab．2 Result of three energy storage ways

4 结论

(1)同时负荷的缺电率和负荷的最大瞬时功率缺失来确定储能容量的大小，得出的优化容量是较为准确的。

(2)在同时考虑负荷缺电率和储能系统实际的功率输出能力 (即表现在储能系统的放电速率)时，由超级电容器和蓄电池组成的混合储能系统能提高风光互补发电系统的经济性、可靠性。

［1］冬雷，廖晓钟，刘广忱，等．分布式风光互补发电系统及其多目标优化控制策略研究［J］．仪器仪表学报，2005，(2):750-753．Dong Lei，Liao Xiaozhong，Liu Guangchen，et al．Multi-index optimization control strategy based on distributed PV and wind energy complemental generation system［J］．Chinese Journal of Scientific Instrument，2005，(2):750-753．

［2］赵波，李鹏，童杭伟，等．从分布式发电到微网的研究综述［J］．浙江电力，2010，(3):1-5．Zhao Bo，Li Peng，Tong Hangwei，et al．Survey on development from distributed generation to microgrid［J］．Zhejiang Electric Power，2010，(3):1-5．

［3］周晓曼．风光互补发电系统［J］．农村电气化，2008，(1):48-49．Zhou Xiaoman．Wind/PV hybrid generation system ［J］．Rural Electrification，2008，(1):48-49．

［4］徐大明，康龙云，曹秉刚．风光互补独立供电系统的优化设计［J］．太阳能学报，2006，27 (9):919-922．Xu Daming，Kang Longyun，Cao Binggang．Optimal design of standalone hybrid wind/PV power systems［J］．Acta Energian Solaris Sinica，2006，27 (9):919-922．

［5］谈蓓月，卫少克．风光互补发电系统的优化设计［J］．上海电力学院学报，2009，25 (3):244-248．Tan Peiyue，Wei Shaoke．Optimization design of wind/PV hybrid system［J］．Journal of Shanghai University of Electric Power，2009，25 (3):244-248．

［6］Zhao Y S，Zhan J，Zhang Y，et al．The optimal capacity configuration of an independent wind/PV hybrid power supply system based on improved PSO algorithm［C］．International Conference on Advances in Power System Control Operation and Management，2009．1-7．

［7］鲁蓉，张建成．超级电容器储能系统在分布式发电系统中 的 应 用 ［J］．电 力 科 学 与 工 程，2006，22(3):63-67．Lu Rong，Zhang Jiancheng．Application of super capacitor energy storage system to distributed generation system［J］．Electric Power Science and Engineering，2006，22 (3):63-67．

［8］唐西胜，齐智平．超级电容器蓄电池混合电源［J］．电源技术，2006，30 (11):933-936．Tang Xisheng，Qi Zhiping．Study on the ultracapacitor/battery hybrid system ［J］．Chinese Journal of Power Sources，2006，30 (11):933-936．

［9］Testa A，S De Caro，R La Torre，et al．Optimal design of energy storage systems for stand-alone hybrid wind/PV generators ［C］．International Symposium on Power Electronics Electrical Drives Automation and Motion， 2010．1291-1296．

［10］桂长清．实用蓄电池手册［M］．北京:机械工业出版社，2011．35-37，397-398．

［11］雷肖，马历．蓄电池荷电状态闭环动态估算模型［J］．电源技术，2008，32 (6):398-401．Lei Xiao，Ma Li．Close-loop dynamic estimation model for battery state of charge ［J］．Chinese Journal of Power Sources，2008，32 (6):398-401．