高密度聚乙烯结构发泡塑料拉伸本构关系的研究
饶聪超,姜献峰,李俊源,杨德伟,陈林林
(浙江工业大学特种装备制造与先进加工技术教育部重点实验室,浙江 杭州310014)
0 前言
PE-HD结构发泡材料是以聚乙烯(PE)为基体,采用注射发泡工艺生产制作而成的,内部含有大量闭孔,表皮相对致密的多孔材料,如图1(a)所示。其独特的微观结构决定了发泡塑料具有优良的力学和多功能特性。目前国内外学者主要是针对均匀泡沫塑料的力学性能展开研究,如图1(b)所示。结构发泡塑料由于泡孔的非均匀性,虽然改善了发泡塑料的力学性能,但同时也使本构关系变得更为复杂。

图1 发泡材料Fig.1 Foaming materials
耿皓[1]通过PE泡沫塑料的压缩实验,研究了其均匀发泡材料的应力-应变特性及其应变率效应。卢子兴[2]通过3种密度硬质聚氨酯泡沫塑料的拉伸实验,研究了该均匀发泡材料的拉伸本构关系。对于结构发泡材料,目前国内外研究较少,对结构发泡的研究大多停留在原料改性,制品合成和加工工艺上。为此,本文基于Sherwood-Frost模型,研究PE-HD结构发泡材料的力学特性,通过将结构发泡塑料材料均质化的思路,建立了拉伸本构关系,用数值方法拟合了包括应变率、密度效应的相关参数。
1 拉伸本构关系的建立
发泡塑料本构关系的确定有2种类型:半经验型和经验型。前者从一些基本理论出发得到本构关系的具体形式,方程中的参数需根据实验数据拟合而定。目前对泡沫塑料大多采用经验型模型。Sherwood和Frost在建立泡沫塑料本构关系时将环境温度和密度及应变率等因素考虑进去,提出了如下较为全面的经验型本构关系[3]:

式中σ——加载应力,MPa
T——环境温度,℃
ρ——泡沫材料的密度,g/cm3
其中H(T)主要反映了环境温度对应力的影响,G(ρ)代表密度对应力的影响;而反映了应变率对应力的影响;形状函数f(ε)定义为某一参考样条在其参考密度、参考应变率、准静态加载下的应力-应变函数关系式。式(1)能较好地模拟材料变形的全过程。
胡时胜等[4]基于Sherwood-Frost本构模型,考虑了密度和应变的耦合,对其中的密度项进行了修正,将G(ρ)改写为G(ρ,ε),并结合试验拟合了包含应变率效应的压缩本构关系。对于PE-HD结构发泡塑料,本文在基于上述思想的基础上,仍选取如下的本构关系式:
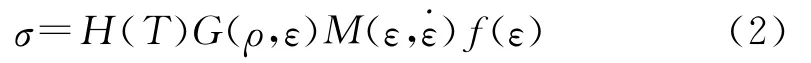
1.1 密度的影响
李俊等[5]在建立低密度聚乙烯(PE-LD)泡沫塑料的压缩本构关系时,将应变和密度耦合成幂指数形式。本文也将G(ρ,ε)以一种幂指数关系式表示:
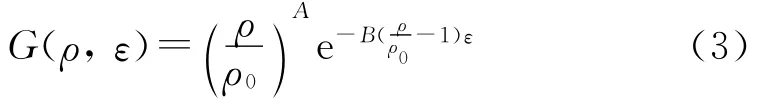
式中ρ0——参考密度,g/cm3
A、B——相关参数
1.2 应变率的影响
应变率对应力-应变曲线的影响同样采用基于热激活机制提出的Seeger模型[6]加以描述,即:
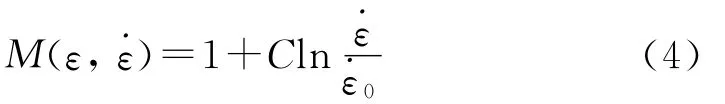
C——相关参数
1.3 形状函数
形状函数实质上是一具体的参考样条在其参考应变率、参考密度下的应力-应变关系,描述多孔介质材料特有的变形3阶段。Rush[7-8]提出了静态下的本构关系,并给出了形状函数相应的关系式;Schwaber等[9]将形状函数写为多项式形式。本文也采用多项式形式来描述形状函数,即:

式中n、Ai——拟合参数
若拉伸试验是在恒定温度下进行的,H(T)就为常数,该项可以合并在形状函数中表示,所以此时的PEHD结构发泡材料拉伸本构方程可表示为:

2 模型参数拟合
2.1 参考样条拉伸试验计算
选取参考样条,对参考样条做拉伸测试,此时ρ=,则式(6)可简化为式(7)。
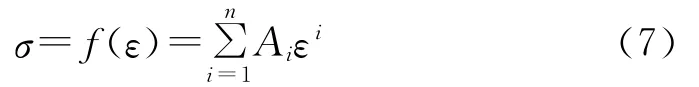
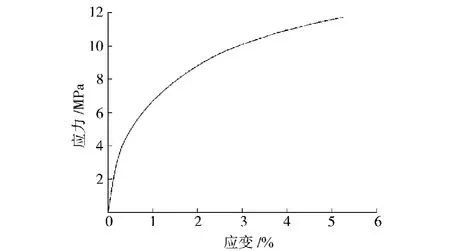
图2 参考应变率下的PE-HD结构发泡塑料拉伸应力-应变曲线Fig.2 Tensile stress-strain curve for PE-HD structural foamunder reference strain rate
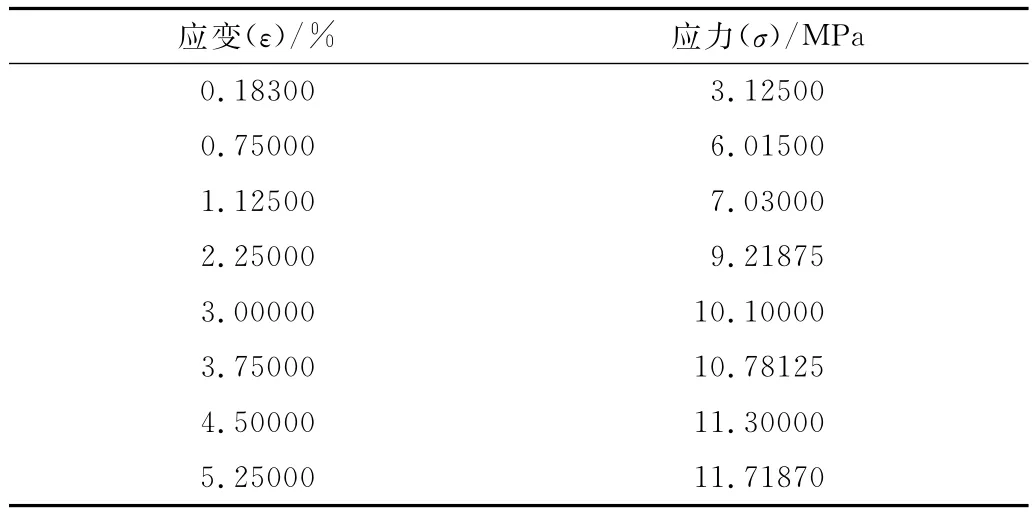
表1 参考样条的应力-应变值Tab.1 Stress-strain values for the reference spline

表2 f(ε)各参数值Tab.2 Parameters of f(ε)

图3 实验曲线和拟合曲线Fig.3 Experimental curve and fit curve
2.2 模型参数计算结果
选取另一样条做拉伸试验,如图4所示的拉伸应力 -应变曲线,此时从拉伸试验数据中选取的一些应力-应变值,如表3所示,同时将参考样条的应变率一起代入到式(6)中,整理计算可得出式(8)的表达形式 (i取1~8)。

对于不同的i取值,根据表3将应力-应变值分别代入式(8)后两两相除,得到B(ρ1/ρ0-1)的平均值为-0.0074,并将其代回式(8)中可得到(ρ1/ρ0)A(1-1.61C)的平均值为1.04。
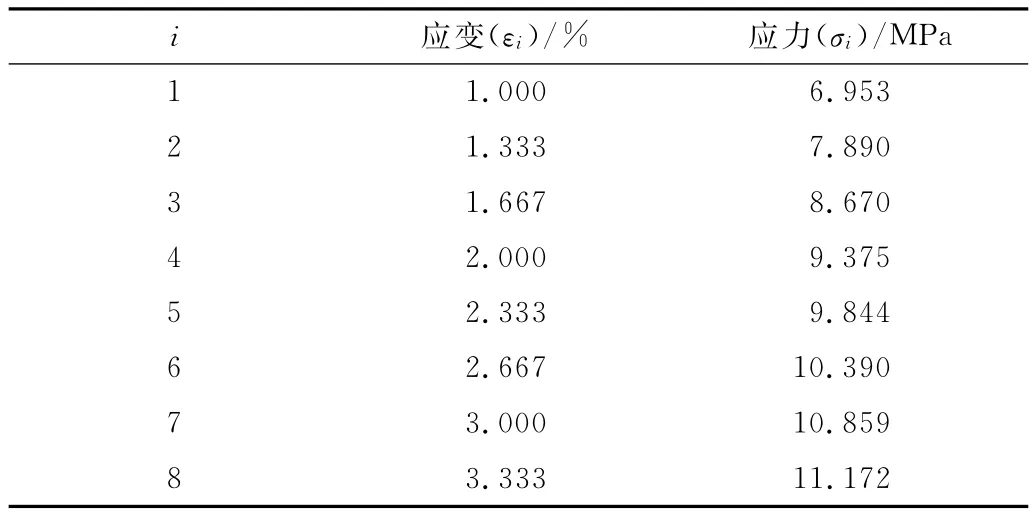
表3 另一样条的应力-应变值Tab.3 Stress-strain values for another spline

图4 另一样条的拉伸应力-应变曲线Fig.4 Tensile stress-strain curve for another spline
胡时胜等[4]在基于Sherwood-Frost模型对硬质聚氨酯泡沫塑料本构关系研究时,得出A=2.052,C=0.0829;李俊等[5]在Sherwood-Frost模型的基础上,建立了PE-LD泡沫塑料的压缩本构模型,得出A=6.7435,C=0.0597。本文研究的PE-HD结构发泡材料与硬质聚氨酯泡沫材料弹性模量较为接近,所以分析对比材料的力学特性,并依据多孔材料弹性模量与相对密度的关系[10],最终选取A=2,C=0.08。
将A、C的值代入(ρ1/ρ0)A(1-1.61C)中,便可得ρ1/ρ0=1.09;再把ρ1/ρ0的值代回式(8)中,得出B=-0.082。本文的拉伸样条是从同一结构不同部位选取的,因此发泡程度大致相同。从计算结果ρ1/ρ0=1.09可知,结构发泡材料的不同部位存在密度差异。
如图5所示提出的本构模型拟合计算的PE-HD结构发泡塑料材料的应力-应变曲线和试验结果的对比。拟合计算结果表明,本构关系对PE-HD结构发泡塑料材料的实验数据能实现良好的拟合,模型能较好地反映材料静态单轴拉伸下的力学行为。
3 结论
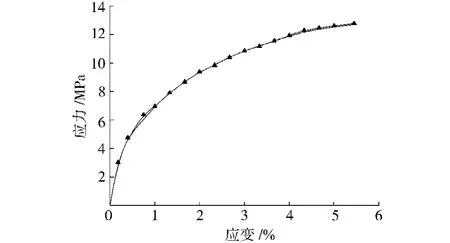
图5 实验与计算曲线的比较Fig.5 Comparison of experimental curve with calculating curve
(1)基于 Sherwood-Frost模型建立了 PE-HD 结构发泡塑料的拉伸本构模型,通过拉伸试验数据拟合了材料参数,并通过试验验证该模型,提出的本构模型和实验结果比较吻合;所建立的拉伸本构模型反映了不同密度和不同应变率对其力学特性的影响,为研究建立比较全面的材料模型提供了一定的参考和依据;
(2)本文研究的PE-HD结构发泡拉伸本构关系涉及了材料密度及应变率,能够实现较好地拟合;
(3)本文在恒温下进行的拉伸试验,没有考虑温度的影响,但实际工作中环境温度变化对材料也有一定的影响,这需要进一步探讨;
(4)由于结构发泡材料同一部件的不同部位存在密度差异,所以标准试件的制取必须考虑密度的差异。
[1] 耿 皓.聚乙烯泡沫塑料的静态压缩性能研究[J].应用科技,2006,33(1):62-64.Geng Hao.Study of the Performance of Static Compression of Polyethylene Foamed Plastics[J].Applied Science and Technology,2006,33(1):62-64.
[2] 卢子兴.聚氨酯泡沫塑料拉伸本构关系及其失效原理的研究[J].航空学报,2002,23(2):151-154.Lu Zixing.Investigation into the Tensile Constitutive Relation And Failure Mechanism of PUR Foamed Plastics[J].Acta Aeronautica et Astronautica Sinica,2002,23(2):151-154.
[3] Sherwood J A,Frost C C.Constitutive Modeling and Simulation of Energy Absorbing Polyurethane Foam[J].Polymer Eng Sci,1992,16:1138-1146.
[4] 胡时胜,刘建飞,王 悟.硬质聚氨酯泡沫塑料本构关系的研究[J].力学学报,1998,30(20):151-156.Hu Shisheng,Liu Jianfei,Wang Wu.Study of the Constitutive Relationship of Rigid Polyurethane Foam[J].Acta Mechanica Sinica,1998,30(20):151-156.
[5] 李 俊,高 德,王振林.低密度聚乙烯泡沫塑料压缩本构关系的研究[J].包装工程,2008,29(12):25-26.Li Jun,Gao De,Wang Zhenlin.Study of the Constitutive Relation of LowDensity Plyethylene FoamUnder Compression[J].Packaging Engineering,2008,29(12):25-26.
[6] 胡仁伟,刘文珽.腐蚀条件下耐久性分析概率断裂力学方法研究 [J].固体力学学报,1998,19(S):28-33.Hu Renwei,Liu Wenting.Probabilistic Fracture Mechanics Approach for Durability Analysis In Corrosive Environment[J].Acta Mechanica Solida Sinica,1998,19(S):28-33.
[7] Rusch K C.Load-compression Behavior of Flexible Foams[J].Journal of Applied Polymer Science,1969,13:2297-2311.
[8] Rusch K C.Load-compression Behavior of Brittle Foams[J].Journal of Applied Polymer Science,1970,14:1263-1276.
[9] Schwaber D M,Meinecke E A.Energy Absorption in Polymeric Foams.II.Prediction of Impact Behavior from Instron Data for Foams with Rate-dependent Modulus[J].Journal of Applied Polymer Science,1971,15:2381-2393.
[10] Gibson L J,Ashby MF.Cellular Solids:Structure and Properties[M].Oxford:Pergamon Press,1988:65-90.
——机理与材料》简介
——机理与材料》简介

