基于EMD和干预分析的电力系统短期负荷预测

顾 洁，包海龙，唐 衍

（1.上海交通大学 电气工程系，上海 200240；2.上海电力公司，上海 200122）

短期负荷预测对于电力系统的安全经济稳定运行至关重要，国内外对此开展了广泛研究。在电力工业市场化改革及智能电网建设的大背景下，短期负荷预测工作中存在不少急需解决的问题，例如：短期负荷预测一般是提前1天以上对预测时刻的负荷值做出估计[1]。目前的研究表明，将每一日的各时刻点的负荷作为一维向量处理是一种比较有效的方式，其本质可视为对向量时间序列的预测，这样的处理固然简化了分析过程，却忽略了时间序列向量中包含的很多信息，因而影响预测的精度[2—4]。

此外，气象因素对短期负荷变化规律具有显著的影响，这一点无论在电力负荷预测理论与方法的研究领域还是实际电网的预测工作中，都得到了公认[1—3]。国内外电力负荷预测工作中对气象因素的处理主要经历过4个阶段：①完全不考虑气象因素影响的阶段[3]，比较多的是直接采用自回归移动平均模型（auto-regressive and moving average model，ARMA）或其它时间序列模型对短期负荷序列建模外推，往往不去考虑负荷序列与气象因素的关系；②采用修正法对不考虑气象因素的结果进行修正的阶段[4]，即应用负荷序列进行外推建模后，利用参考气象因素变化得到的修正系数对预测得到的结果进行修正；③在预测模型中直接加入日气象特征因素的阶段[5]，该类模型在对每日典型气象特征因素筛选的基础上，利用选中的典型气象因素与负荷序列进行建模，采用神经网络建立考虑气象因素的短期负荷预测模型就是其中的典型代表；④在预测模型中直接考虑实时气象因素的阶段，例如：文献[6]、文献[7]就将每小时或每半小时的气象因素作为神经网络的输入构建出考虑实时气象因素的短期负荷预测模型。目前，就气象因素对负荷变化造成的影响单独提取进行分析的相关研究尚较为缺乏。

本文以温度为气象因素代表，应用干预分析理论来提取与处理气温对负荷所造成的影响，将受气温影响而形成的负荷分量序列从原始负荷序列中剔除之后，再运用EMD理论与ARMA理论相结合，进行负荷的分解和预测。这个方法同样可应用于研究湿度、降雨量等其他气象因素对负荷预测的影响。

1 EMD理论及其在短期负荷预测中的应用[8]

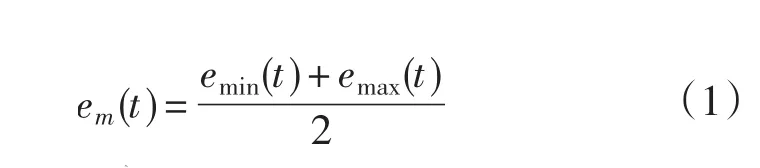
（4）计算信号x(t)与包络均值函数emin(t)的差值函数

（5） 用h(t)代替x(t)，重复以上步骤（2）—步骤（4），直到所得到的包络均值趋于0，这样就得到了第一个基本模式分量（intrinsic mode function，IMF）c1(t)。

由于第一个IMF c1(t)代表的是原始信号中的最高频成分，因此，就可以得到包含原始信号x(t)中低频信号

对x1(t)进行重复步骤（2）—步骤（4），就可以得到第2个IMF c2(t)。如此重复下去，直到得到的差值函数xn(t)是一个常值函数或者单调函数，原始信号x(t)就可以由这些IMF函数cj(t)（j=1，2，……，n）和趋势函数rn(t)来表示，如式（4）所示

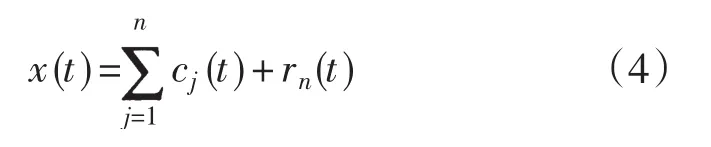
1.1 EMD分解的实现步骤

对于给定的信号x(t)∈R1，其EMD分解的实现步骤如下：

（1）找到x(t)所有的局部极值点。

（2）对极大值点和极小值点，利用样条插值的方法分别建立信号的极大值包络函数和极小值包络函数，并分别记为emax(t)和emin(t)。

（3）计算上包络函数和下包络函数的均值函数

1.2 基于EMD的短期负荷预测模型[8]

负荷序列中的随机成分往往对负荷预测精度有较大影响，因此，利用经验模态分解将原负荷序列中的高频随机分量提取出来，根据其特点分别进行建模预测。文献[8]中提出了基于EMD的短期预测模型，但是该模型未能充分计及气象因素对负荷变化的影响，在降温或取暖负荷所占比重较大的地区，可能会降低预测的准确度，因此引入干预分析模型，提取气象因素对短期负荷增长的影响，进一步改善预测效果。

2 干预分析模型理论[9]

2.1 干预分析模型的基本概念

采用时间序列来描述经济等变量的变化过程时，变量受到特殊因素或者事件及态势的影响，其变化规律发生了改变，例如：在进行电力负荷预测时，我国目前大力推行的节能减排政策的影响；国际金融危机的爆发对电力需求的影响等，因此必须在预测和分析过程中对这类特殊因素或事件所产生的影响进行剥离，称这类外部事件为干预。

干预分析研究旨在就政策干预或突发事件对目标对象变化过程的影响进行具体量化分析。美国威斯康辛大学统计系教授博克斯与泰奥1975年联合发表了一篇题为《经济与环境问题的干预分析及应用》的论文，在文中提出了干预分析的基本理念。此后，干预分析的概念和干预分析模型引起了人们广泛关注，并迅速地被应用去描绘政策的变化及其给经济等带来的影响。

2.2 干预变量分类

干预变量是干预分析模型中的基本变量，根据干预的特点可分为2种基本形式：

（1）持续性的干预变量，形式如式（5）所示

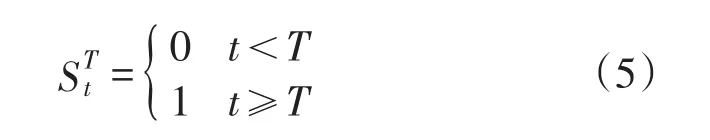
式中：T为干预发生时间；t≥T代表干预事件发生之后；t＜T代表干预事件发生之前；StT代表t时刻的持续性干预变量。

（2）短暂性的干预变量，形式如式（6）所示

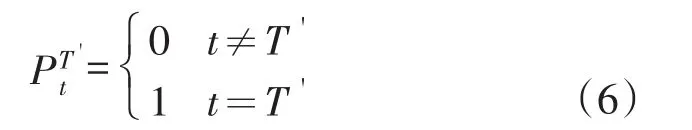
式中：t为时间变量；'表示干预事件发生时间；'代表干预的发生时间；'为其他时间；PT't为t时刻的短暂性干预变量。

2.3 干预事件的影响

干预事件的影响形式可归纳如下[10]：

（1）干预事件的影响突然开始，长期持续下去，干预模型

式中：w表示干预影响强度的未知参数；Yt表示干预模型的输出。

如果Yt要求通过差分化为平稳序列，则干预模型可调整如式（8）所示

式中：B为后移算子。

如果干预事件要滞后b个时期才产生影响，干预模型可调整如式（9）所示。

（2）干预事件影响逐渐开始，长期持续下去，干预模型式中：δ为表征干预影响长度的重要参数，需要通过具体的回归建模后求取，0＜δ＜1。

当δ=0时，干预的影响只存在一个时期；δ=1时，干预的影响将长期存在。

（3）干预事件突然开始，产生暂时的影响，干预模型

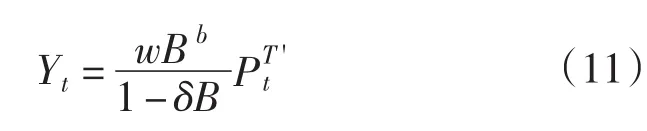
式中：0＜δ＜1。

（4）干预事件逐渐开始，产生短暂的影响，干预模型

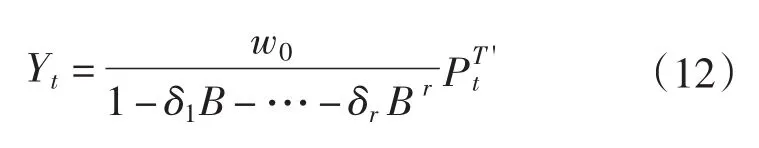
式中：r代表后移阶数，r≥2。

显然，实际系统中受到的复杂干预影响可以用上述4种形式或者其组合来表达。

3 基于干预分析的电力系统短期负荷预测模型[10]

3.1 基于干预分析的负荷预测模型建模思路

鉴于气候因素对短期负荷变化规律有较大影响，引入干预分析理论在短期负荷预测中较为合理地处理气候因素影响，以改善预测效果。

预测模型的建模思路可以概括如下：

（1）利用干预影响前的数据(即t＜T时间段内的实际负荷序列值)，建立时间序列模型并进行外推，外推结果作为未受干预影响的负荷值。

（2）将实际值减去前述外推结果，得到受干预影响值，基于此求取干预影响模型参数。

（3）利用原始序列与干预序列的差构成消除干预影响后的序列（即净化序列），对净化序列建立相应的时间序列模型。

（4）将步骤（3）得到的时间序列模型与干预模型分量结合，得到综合预测模型。

由于气象因素对电力负荷的影响一般不是即刻和完全释放出来的，而是随着时间的推移，逐渐地体现出其效果，例如：夏天负荷的气温累积效应等。可根据式（12）进行建模，其中后移阶数r可在根据实际问题的特点确定。通过数据分析后得出，气温序列2阶滞后序列与负荷序列相关性最高，故选取干预影响后移阶数为2。因此确定干预影响建模的模型如式（13）所示。实际应用时可按具体问题采用相应的滞后阶数进行干预建模。

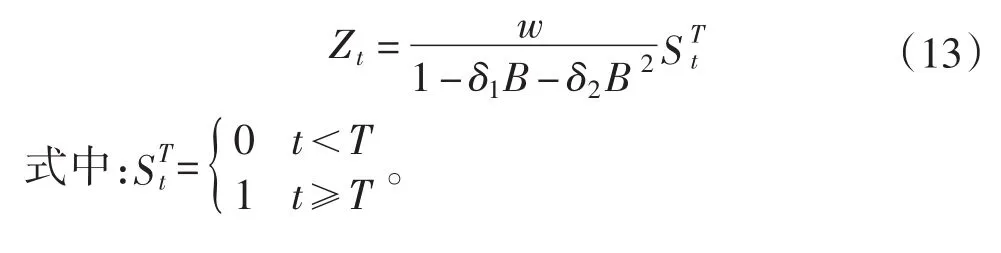
3.2 预测模型的实现过程

（1）利用干预影响产生前的数据，建立单变量时间序列模型At。

采用差分自回归移动平均模型（autoregressive integrated moving average model,ARIMA）对干预影响产生前的数据序列进行建模。应用单位根检验的方法来判断数据序列的平稳性后确定是否需要进行差分。

（2）干预影响模型的参数估计[10]。

以ARMA模型外推结果作为未受干预影响的时间序列预测值，实际观测值与该预测值的差即视为该干预变量的影响Zt

式中：xt为原始负荷数据序列。

干预影响模型的参数可按式（13）得到。

（3）得到消除干预影响后的净化负荷，对该序列进行建模预测。

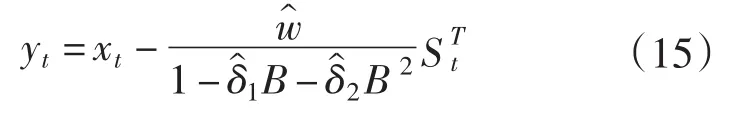
净化序列计算如式（15）所示式中：yt为净化后的负荷序列；xt为原始负荷数据序列。

对净化后的负荷序列yt建立ARMA模型。

（4）建立综合预测模型。将步骤（3）中所建立的ARMA模型与步骤（2）中所建立的干预模型进行叠加，即得到最终的综合预测模型。

整个预测模型的基本流程如图1所示。基于净化序列建立EMD分解与ARMA相结合的预测模型进行预测，得到最终预测结果。参考文献[8]详细说明了EMD分解与ARMA相结合的预测模型的理论基础。

4 算例结果与分析[10]

选取我国南方某地区电网2008年4月1日至2008年9月30日间每日整点负荷作为原始数据。列出以4月1日至6月30日的数据作为已知量，预测7月1日至7月14日之间的负荷值的预测结果。为了减小或消除一天之内的负荷周期性变化的干扰，需要进行负荷数据的预处理，应用HP滤波，消除周期分量影响，对处理后的趋势分量进行建模分析。篇幅所限，图2中列出了2008年7月1日—7月2日直接应用EMD分解与ARMA结合的模型和应用本文提出的模型得到的整点预测结果，按1—48的顺序排列。表1显示了2008年7月短期负荷预测误差统计。

图3为EMD-ARMA模型与干预分析EMD模型2种预测所得到的相对误差曲线。图中实线代表EMD-ARMA模型预测的相对误差，虚线代表干预分析EMD模型预测的相对误差，图中明显反映出，虚线区间几乎被实线包围着，说明虚线所对应的预测模型得出的相对误差更小。

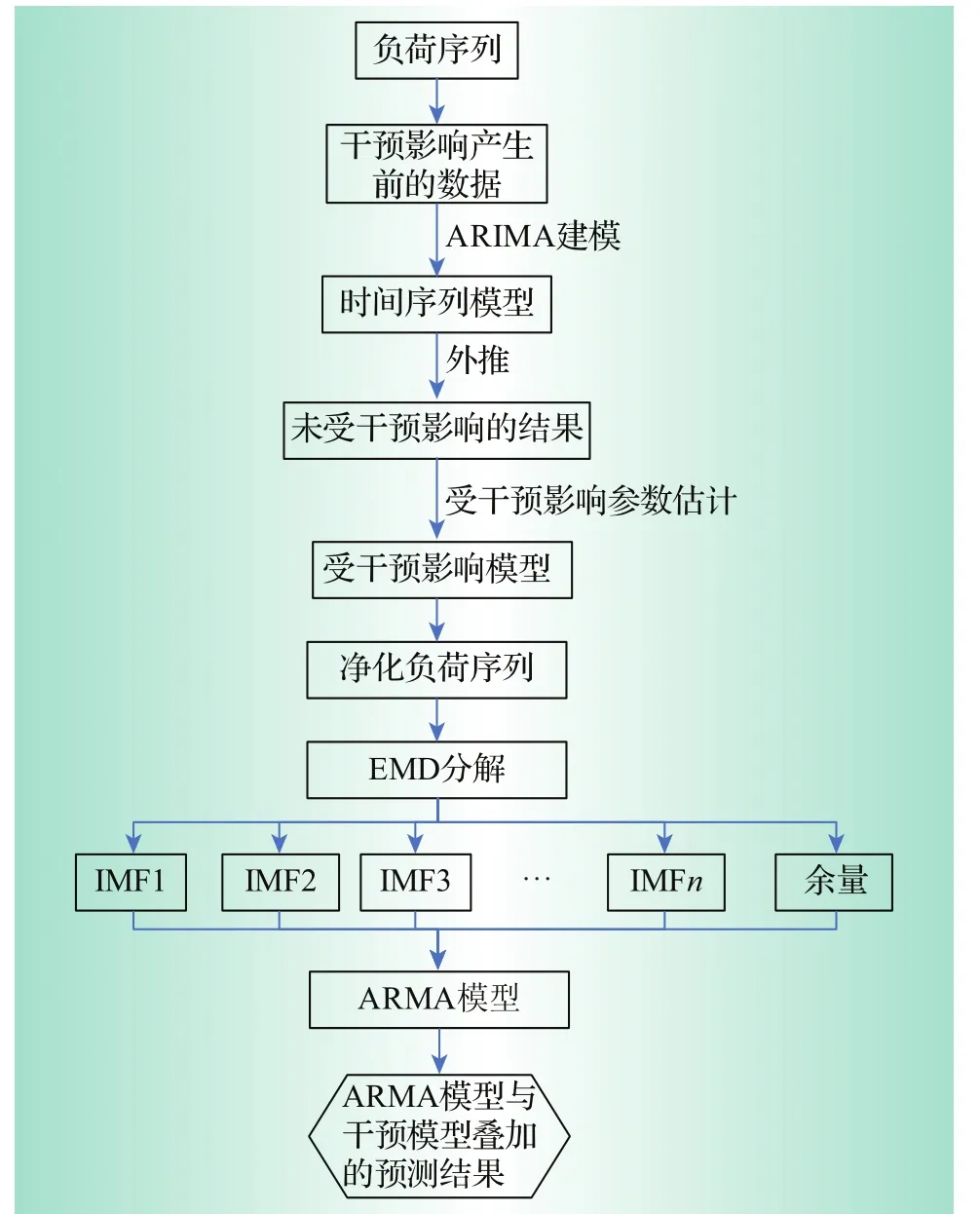
图1 基于干预分析的短期负荷预测模型

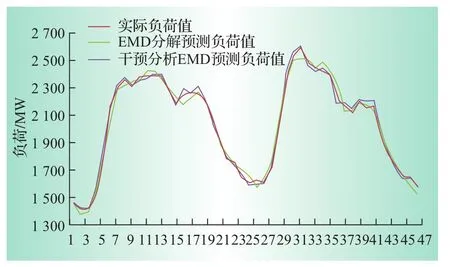
图2 2008年7月1—2日短期负荷预测结果

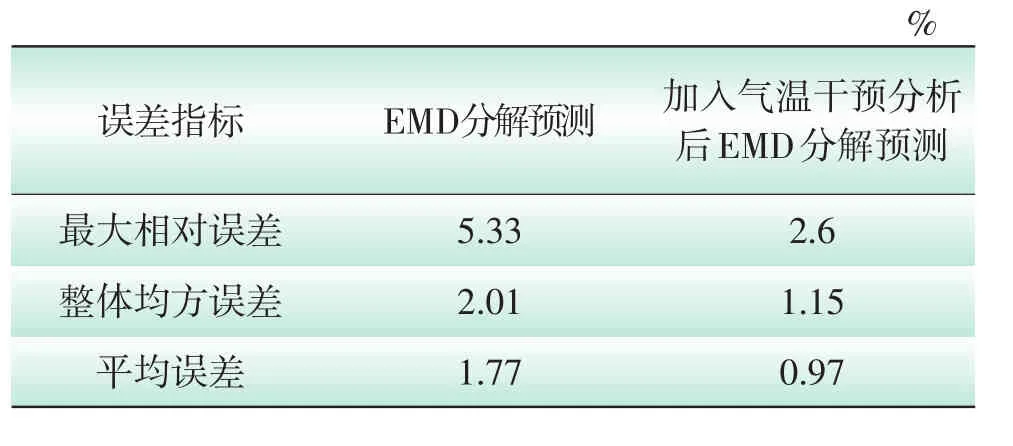
表1 2008年7月短期负荷预测误差统计

实例验证的结果表明，在短期负荷预测中，气温对预测精度的影响较为显著，采用干预分析对于提高预测的精度，减小预测误差有一定的参考价值。

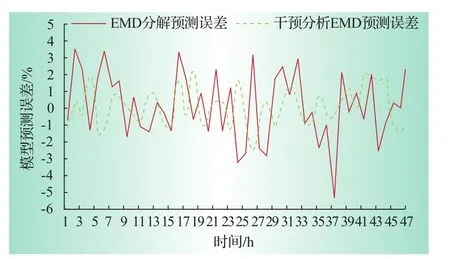
图3 2008年7月1—2日短期负荷预测误差

5 结论

气象因素对短期负荷变化造成的影响是电力系统短期负荷预测中必须关注的问题。本文提出的将干预分析与EMD分解理论相结合的预测模型，通过对气象因素所造成的影响进行提取和剥离，使得EMD分解所处理的序列为净化后序列，增强了序列的可外推性，从而有助于提高模型整体预测精度。实际系统负荷预测的结果表明，采用干预分析处理后，模型预测误差较小，与不经过干预分析直接进行EMD-ARMA预测得到的结果相比，在最大误差、平均误差等误差统计指标上，均有较明显改善，是提高短期负荷预测精度的一项有益的尝试。

［1］ 康重庆,夏清,刘梅.电力系统负荷预测[M].北京：中国电力出版社,2007.

［2］ 罗玮,严正.基于广义学习矢量量化和支持向量机的混合短期负荷预测方法[J].电网技术,2008,32(13)：62-68．

［3］ 林辉,刘晶,郝志峰,等.基于相似日负荷修正的节假日短期负荷预测[J].电力系统保护与控制,2010,38(7)：47-51.

［4］ 朱陶业,李应求,张颖,等.提高时间序列气象适应性的短期电力负荷预测算法[J].中国电机工程学报,2006,26(23)：14-19.

［5］ 刘旭.基于实时气象因素的短期负荷预测方法研究[D].长沙：湖南大学,2009.

［6］ 刘旭,罗滇生,姚建刚,等.基于负荷分解和实时气象因素的短期负荷预测[J].电网技术,2009,33(12)：94-100．

［7］ 方鸽飞,胡长洪,郑奕辉,等.考虑夏季气象因素的短期负荷预测方法研究[J].电力系统保护与控制,2010,38(22)：100-104．

［8］ 唐衍,顾洁,张宇俊,等.基于EMD理论的短期负荷预测[J].电力需求侧管理,2011,13(1)：15-19.

［9］ 易传和,刘波.基于误差修正模型的股市逆向干预政策时效分析[J].系统工程,2009,27(6)：38-41.

［10］ 唐衍.基于EMD方法的电力系统短期负荷预测[D].上海：上海交通大学,2011.