双馈异步发电机通风冷却综合计算

张志强，戈宝军，吕艳玲，陶大军

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨150080)

0 引言

随着电机工业的进步，电机材料成本的增加，对电机体积、效率、温升的设计都提出了更高的要求。电机的温升直接关系到电机的性能和经济指标，这就需要对电机内的通风与温升进行准确的计算，合理地分配电机内冷却介质，使电机的发热部件得到良好的冷却，从而降低电机温升，提高系统效率。

对电机的通风系统进行优化，就是要对电机的通风总量，各风道的流量分配，以及局部风损等目标函数进行优化计算，这需要考虑到压源与沿程损失、局部损失之间的相互影响，还要考虑转子径向风道的等效风扇效应、转子旋转等诸多因素的影响[1-2]。近年来诸多国内外的学者通过引入现代数值计算手段[3-5]，在本领域展开了广泛深入的研究。目前针对电机通风计算有两种主流算法，其一是通过有限差分、有限体积及有限单元等数值算法，建立电机通风的三维模型，如温嘉斌、路义萍等运用计算流体动力学对发电机转子风道结构与流量分布的关系进行了较为深入的研究[6-9];李伟力、丁树业等则利用有限体积法给出了发电机定子内通风沟内多元流场流速、换热系数及温度场的分布规律[10-12]。三维模型能够反映出通风、温度等局部细节状态，但易受硬件条件的限制，其模型选取往往具有局限性，边界条件不易确定，对于系统整体的通风计算较难实现。在分析系统整体通风分布时一般都采用具有集总参数的等值风路求解，如许承千、魏永田等学者给出的电机冷却系统的等效通风网络算法[13-18]。本文在已有研究的基础上，根据样机通风系统的特点，建立适用于具有本样机通风系统特点的通风数学模型，对各风道的流量分布及影响其分布的转速、径向风道尺寸等因素进行分析，为样机通风系统的优化设计提供理论依据。

1 通风模型

1.1 物理模型

本文以3 MW双馈异步电机为研究对象，机座、机壳铺设水套冷却器，内部采用轴径混合通风方式进行冷却。空气经机座水套冷却器冷却后，进入到定、转子端部，然后分别通过定子压板的风孔、气隙及转轴上的供风路进入到电机内部各风道，对电机内部进行冷却，最后被加热的空气在电机另一端汇合回到径向离心风扇。电机通风冷却系统如图1所示。

图1 电机冷却系统Fig.1 Cooling system of the generator

1.2 基本假设

为了便于电机的通风分析，根据电机内冷却系统的特点，对分析模型做出如下假设:

1)流体不可压缩;

2)流体是连续介质，流量、压力均连续变化;

3)流体的流动属于定常流动，流场中各点的流速、密度、压力等物理量不随时间变化;

4)空气密度相对较小，且电机尺寸有限，所以不计总流能量方程中位势能的变化。

1.3 多风路通风系统的数学模型

空气在风道内流动的过程中，压力、速度和位置都是不断变化的，针对简单风道中不可压流体的恒定流动总流的能量方程[19]为

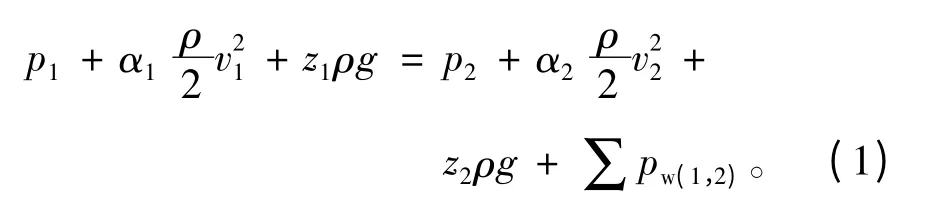
式中:p1、p2分别为风道截面1及2处的动压;v1、v2分别为风道截面1及2处的平均流速;α1、α2为动能修正系数;ρ为空气密度;z1、z2分别为截面1及截面2处流体具有的单位位置势能，根据假设z1ρg=z2ρg;∑pw(1，2)为风道截面1及截面2之间的沿程阻力和局部阻力的水头损失之和。

在电机通风系统中，除了有简单的单通道风路外，定子的径向通风沟、转子的径向通风沟等形成了较为复杂的多支路通风系统，针对这类多支路通风结构进一步给出其局部相邻风道通风结构模型，如图2所示。

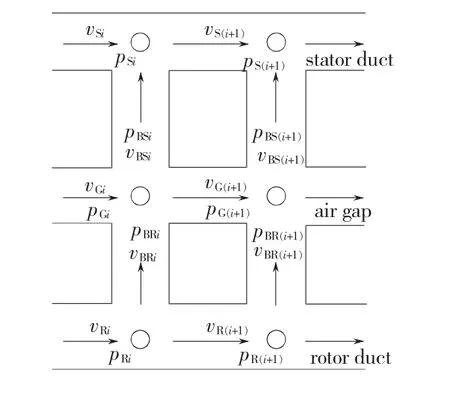
图2 局部相邻风道通风结构Fig.2 Ventilation structure of adjacent ducts

根据图2给出转子相邻两风道的节点i和i+1之间的能量方程为

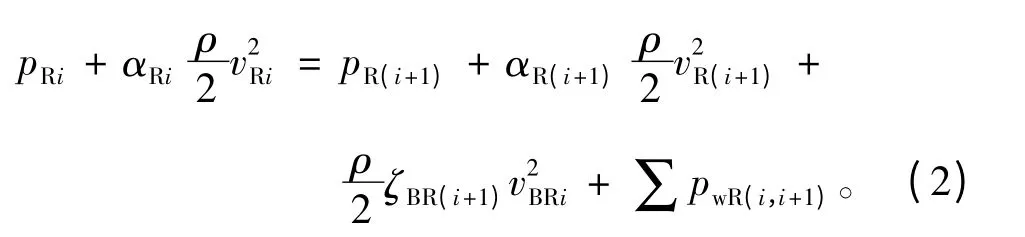
式中:pRi、pR(i+1)分别为转子风道截面i及 i+1处的动压;αRi、αR(i+1)为动能修正系数;vRi、vR(i+1)分别为转子风道截面i及i+1处的平均流速;vBRi为第i段转子分流支路的平均流速为第 i 段径向风道分流而引起的能量损失;ζBR(i+1)为分流阻力系数;∑pwR(i，i+1)为转子风道局部阻力和沿程阻力能量损失之和，其表达式为

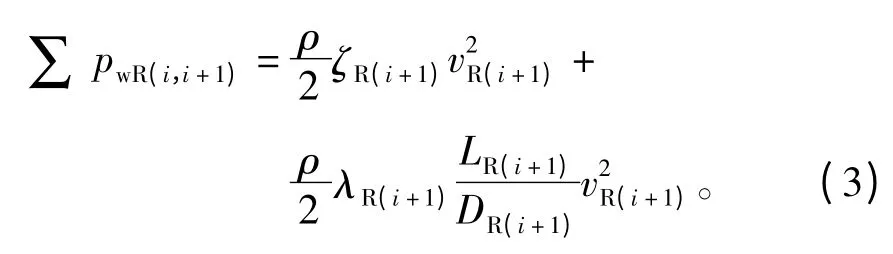
式中:ζR(i+1)为 i+1段的局部阻力系数;λR(i+1)为i+1段沿程阻力系数;LR(i+1)为i+1段风路的长度;DR(i+1)为i+1段风路的特征长度。

由于转子风道处于旋转状态，风道中的流体除了受到重力及摩擦力之外还受到离心力和科赖奥来力，使二次流增加，并产生轴向涡流，导致局部风阻增加，因此需要对风道的局部阻力系数进行修正，修正公式为

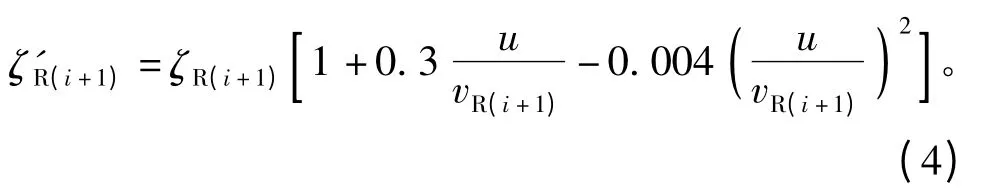
同样根据图2给出定子相邻风道的能量方程为

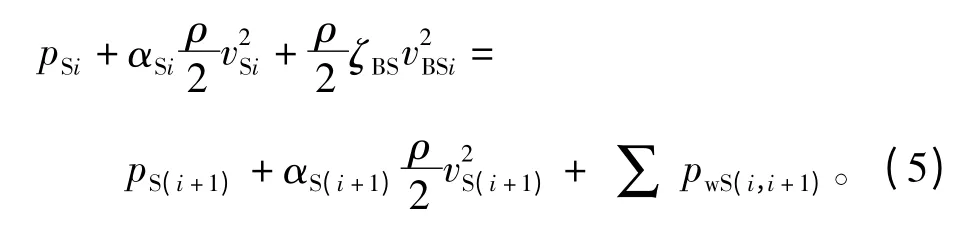
式中:pSi、pS(i+1)分别为定子风道截面 i及 i+1处的动压;αSi、αS(i+1)为动能修正系数;vSi、vS(i+1)分别为定子风道截面i及i+1处的平均流速;ζBS为支路阻力系数;vBSi为第i段分流支路平均流速;∑ pwS(i，i+1)为定子轴向i+1段的局部阻力和沿程阻力能量损失之和。

对于气隙支路，有文献[10]认为异步电机气隙尺寸较小，故气隙中的轴向流动不予考虑。但本文所提到的双馈异步电机气隙相对大些，同时考虑模型的通用性，这里给出气隙上各节点周围断面的能量方程为

式中:pGi、pG(i+1)分别为气隙i及i+1处截面对应的动压;αGi、αG(i+1)为动能修正系数;pBSi、pBRi分别为定、转子第 i段径向风道动压;αBSi、αBRi分别为定、转子第i段径向风道动能修正系数;vGi、vG(i+1)分别为气隙i及i+1处截面的平均流速;∑ pwG(i，i+1)为气隙轴向i段的分流、汇流局部阻力和沿程阻力能量损失之和。

同时对于定、转子径向风道内部给出下面两个方程，即

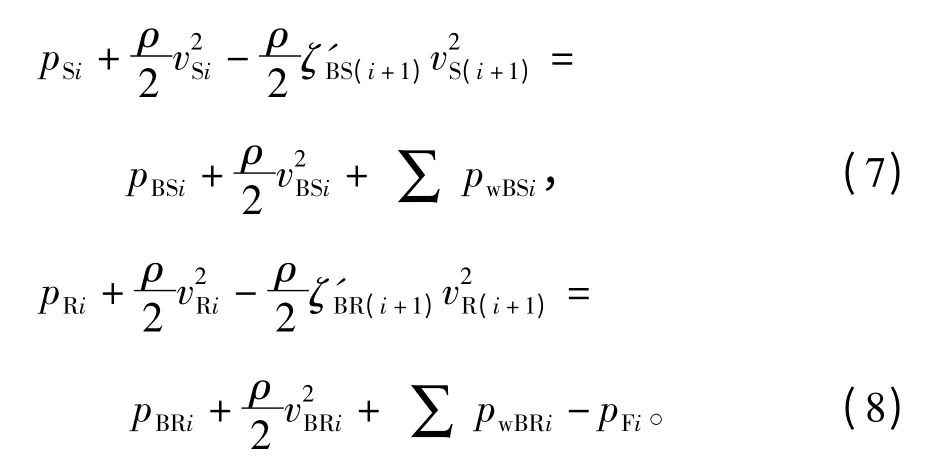
以上各能量方程均是在假设各截面流速分布比较均匀的情况下获得的，流速为各风道的平均流速，其表达式为

式中:vi为第i条风道的平均流速;Qi为第i条风道的体积流量;Ai为第i条风道的截面面积。

通过将上式与各风道的能量方程联立，即可得到用压强和流量来描述的如图2所示的多支路通风系统的非线性方程组，进一步将此局部多支路通风数学描述扩展到整个通风系统，便可得到整个电机通风系统的数学模型。在考虑气隙通风作用的情况下，用压强和流量所描述的电机通风数学模型为三次非线性方程组。当气隙尺寸远小于电机其他风道尺寸，忽略其轴向流动影响时，电机通风的数学模型可简化为二次非线性方程组，给求解带来方便。

2 通风计算结果分析

根据集总参数的等值风路模型，对样机的定、转子等各风道内冷却空气的流量分布进行计算分析。电机定子轴向风道均布在定子轭部，转子轴向供风路均布在轴上。电机设计有13个径向风道，定、转子径向风道一一对应，各风道沿轴向等间距、等宽度布置，宽度d=10 mm。电机的额定功率为3.0 MW，额定转速为1 200 r/min，定子外径为1 100 mm，定子内径为850 mm，转子外径为830 mm，转子内径为500 mm，铁心长1 156 mm。

2.1 额定工况下的通风分析

首先针对额定工况下电机定、转子各风道的体积流量分布进行计算，计算结果如图3所示。

图3 各风道中冷却空气的流量分布Fig.3 Volume flow rate distribution of various air ducts

通过图3(a)转子轴向各风道的流量分布可知，进入转子轴向风道的最大流量为2.34 m3/s，随着各径向风道的分流，流量呈现出非线性的减小趋势。由于转子轴向风道是转子径向风道的供风路，所以其流量的变化趋势也能间接反映出转子径向风道中空气流量的非均匀分布趋势。图3(b)则直接给出了转子各个径向风道的流量计算结果。冷却空气刚刚进入转子轴向的供风路时，轴向流速较快，相对压强较小，所以入口附近径向风道内的流量较小;随着各径向风道的分流，供风路内的空气流量逐渐少，轴向流速不断减小，供风路压强逐渐升高，因此远离入口的径向风道内的空气流量逐渐增加。沿轴向第一个风道内流量为0.247 m3/s，最后一个径向风道流量最大，达到0.473 m3/s。从入风端到出风端，径向风道内的流量分布呈现出先减小后增大的非均匀分布规律。在额定工况下，转子以额定转速高速旋转，使转子各径向风道内产生等效风扇作用，从而导致最小流量风道向中心偏移，出现在中部的7'号风道，流量最小值仅为0.045 m3/s，所有径向风道平均流量为0.135 m3/s。图3(c)和图3(d)为定子各风道中空气流量的分布。由于定子风道既是定子自身的冷却风道也是转子的排风通道，所以定子风道中的流量除了受自身结构限制外，还受转子流量分布的影响。从图3(d)中可以看出，定子径向风道内风量分布与转子径向风道内风量分布呈现出相同趋势，两侧流量大，中部流量小，最大流量出现在出风一侧的13号风道，为0.224 m3/s，最小流量出现在中部的7号风道，为0.030 2 m3/s。图3(e)给出了气隙中冷却空气流量的变化趋势。气隙沿轴向后半段风量逐渐增加，出口一侧空气流量最大值为0.493 m3/s。由计算结果可知，气隙的排风作用不可忽略，所以此电机不宜采用文献[9]中给出的忽略气隙轴向流动的假设条件。

2.2 转子径向风道的等效离心风扇作用

电机运行时，转子的径向风道产生离心风扇作用，为径向风道提供压力升高。转速变化会使转子径向风道所起到的等效风扇作用发生变化，从而引起通风系统内部各风道流量分布产生相应变化，而且由于风道各段的阻力系数是关于流速的函数，也会进一步影响流量的分布。为了讨论转子径向风道等效风扇作用对各风道流量大小及分布的影响，这里假设风道入口的风压、电机通风结构的几何尺寸保持不变。分别对电机转速ω=0 r/min、转速下限ω=620 r/min、额定转速ω=1 200 r/min以及转速上限ω=1 380 r/min时，定、转子径向风道内的流量分布进行对比分析。同时为了能够对比不同流量下定、转子各径向风道分布的变化趋势，引入风道流量偏差比[13]，即

式中:Qi为第i条风道的流量;Qave为与Qi相对应的各风道的平均流量。

图4(a)为不同转速时转子径向风道中的流量分布。从图中可以看出，不同转速时各径向风道内的流量分布整体趋势基本一致，靠近入口侧径向风道内的流量较小，靠近出口侧径向风道内的流量较大。在转子旋转时，会在转子径向风道内形成一个压力升高，从而改变风道的静压分布状况，径向风道流量增加。转速较低时轴向入口侧径向风道的流量远小于出口侧。随转速升高，入口侧径向风道内的流量有较大增加，出口侧也略有增加但不明显，所以径向风道内的流量偏差逐渐减小，如图4(b)所示。径向风道流量偏差的减小，说明径向风道流量分布趋于均衡，也就是各径向风道的换热能力趋于一致，有利于减小转子内部沿轴向的温差。

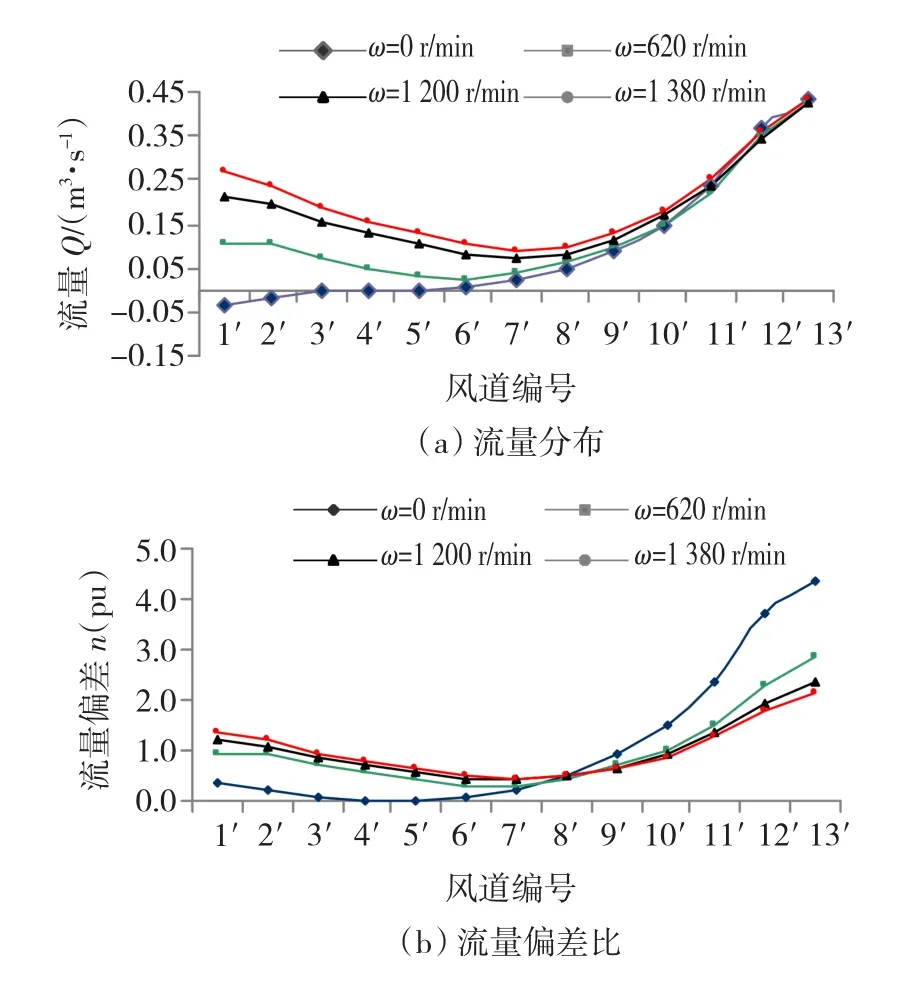
图4 不同转速时，转子径向风道中的流量分布Fig.4 Volume flow rate distribution of rotor radial ducts under different rotor speed

2.3 径向风道宽度对流量分布的影响

由上面的分析可知，在采用径向风道等宽度结构时，沿轴向转子各径向风道内的流量分布呈现出口侧高、中部低的不均衡情况，这会导致转子内部温度沿轴向的分布不均衡。若要改变径向风道内流量的分配，就要改变轴向各段风道的通风风阻的比例。改变风阻可以通过改变通风结构尺寸的方法来实现:1)改变径向风道宽度;2)改变转子供风路截面面积。后一种方法常被用在具有转子副槽通风的大型电机通风系统设计中，通过改变副槽截面积来获得良好的径向风道流量分布，而且改变其面积不会影响轴的强度。而本样机的供风路在转轴上，考虑到轴的尺寸较小，强度受尺寸的影响会很大，所以不采用改变供风路面积的做法，而主要讨论径向风道宽度的变化对流量分布的影响。

在讨论径向风道宽度变化对流量分布的影响时，首先假设电机在额定工况下运行，除径向风道宽度外其他结构尺寸保持不变。为保证轴向安装尺寸不变，要求各径向风道宽度的总长度保持一致。图5为径向风道宽度为等宽度、按等比例减小以及中间宽两侧窄整体呈中心对称这三种结构的转子径向的流量分布。从图中可以看出，采用等宽度分布时出口端径向风道内的流量明显高于入口端和中部，径向风道流量分布严重不均衡。采用入口宽、出口窄，风道宽度沿轴向按一定比例减小的结构形式能够有效增加入口端的流量，但对中部流量影响较小。针对电机流量分布特点，采用中间宽两侧逐渐变窄的结构后，会导致总通风流量略有下降，但其能够有效增加中部径向风道流量，使各风道流量分布趋于均衡，风道间的流量偏差减小，进而减小电机轴向温差。

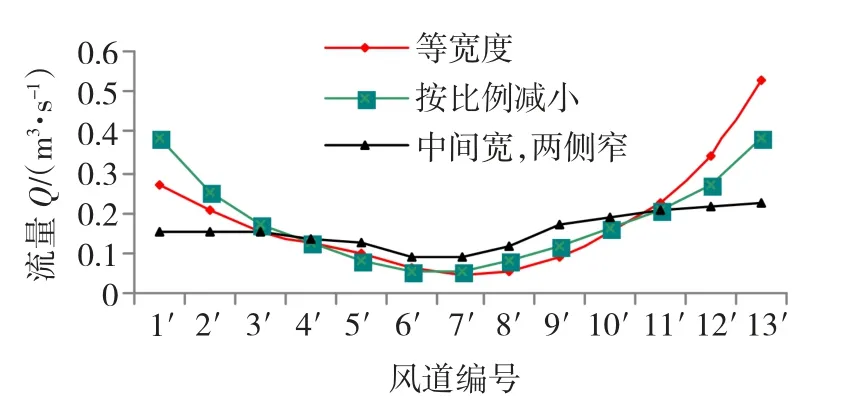
图5 径向风道宽度对流量的影响Fig.5 Volume flow rate distribution under different width of radial duct

3 转子温度计算与分析

通风结构设计的目的就是要降低电机内部的温升，而通风计算一方面可以为通风结构优化提供一定的理论依据，同时也是电机内部温升计算的边界条件。前面分析了转速及结构尺寸对内部通风流量的影响，下面将在前文分析的基础上进一步通过有限单元法来分析电机转子的温度分布。冷风由供风路进入转子径向风道的初始温度分别为59℃和62℃，换热系数由文献[1]提供的方法进行求解。

图6(a)为额定转速运行、径向风道等间距分布时的电机转子的温度场分布。从整体上看，出口温度高于入口温度，气隙侧温度高于轭部温度。最高温位于铁心中部的第6段和第7段，结合通风分析结果来看，在额定转速下，径向风道等距分布时，铁心中部风道的流量小，流速低，换热系数相应较小，导致温升较高。图6(b)为径向风道中间宽、两侧窄这种不等距分布时电机转子的温度分布。由于增加了铁心中部的通风尺寸，使风阻减小，风量增加，同时也减小了单位空间内的热生成率，所以铁心中部的温升下降;对应铁心中部变化，铁心两端风道流量下降，温升都有所上升。为了更直观的对比两种结构对铁心温度分布的影响，给出如图7所示的铁心温度对比。通过对比可知，分布规律基本一致，最热段均出现在齿中部附近，而齿顶和轭部在空气冷却作用下温度略低。径向风道宽度采用不等宽度分布的铁心最热段温度总体上低于等宽度分布的温度。同时图8为二者转子绕组中心线上的温度对比，由图8可知，增加铁心中部径向风道的宽度可以使绕组中部的温度峰值降低，使槽内绕组的温度变化更加趋于平缓。进一步结合图5给出的流量计算结果可知，通过这种形式来改变风道内的流量分布时，流量变化率并不能完全反映出温度的变化率。这是由于增加径向风道的宽度会使风道内的流量增加，但流速并不一定会增加，而流速是决定换热系数大小的主要因素。同时根据能量守恒，在径向风道内部，当冷却空气带走铁心相同热量，流量较大时，温升就会较低，这样铁心和空气的温差会相对较大，温差和换热系数会共同作用来决定最终的换热效果。由分析来看，通过改变中部径向风道的通风尺寸，可以改变各风道的流量分布，进而对铁心内部的温度场分布进行优化，降低温度峰值，使内部温度变化更加趋于平稳。

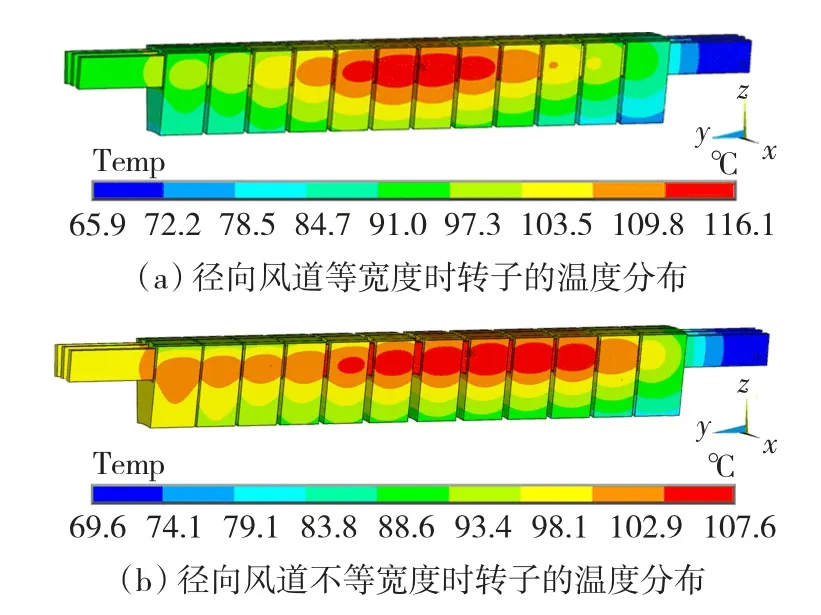
图6 径向风道宽度对温度的影响Fig.6 Temperature distribution under different width of radial duct

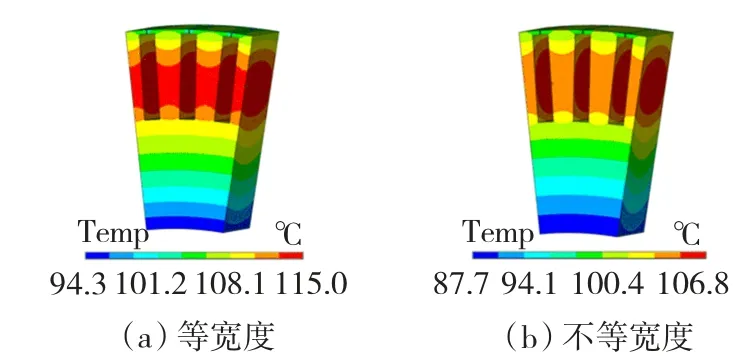
图7 铁心最热段温度分布对比Fig.7 Comparison of temperature distribution between core blocks with highest temperature

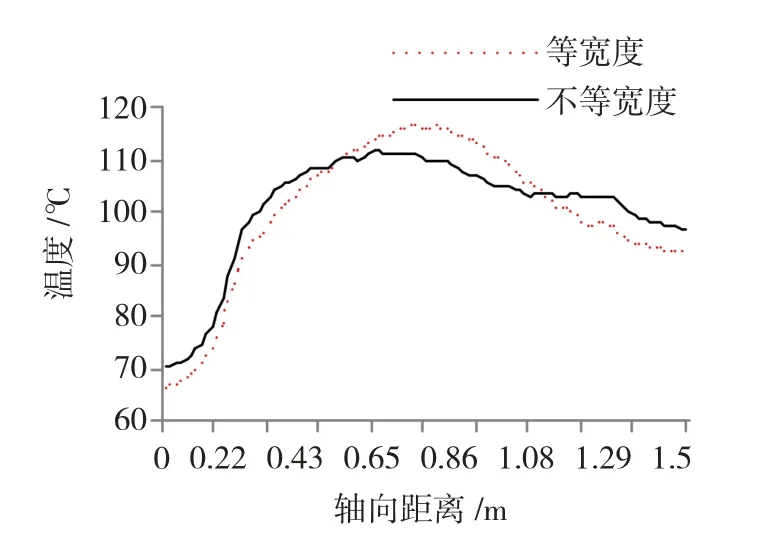
图8 转子绕组中心轴向温度对比Fig.8 Comparison of central temperature distribution between rotor windings under the two different conditions

4 结论

本文以具有轴径混合通风的双馈异步发电机样机为例，给出了电机多风路通风系统的集总参数数学模型，并利用此模型对电机内的风量分布以及可能影响风量分布的转速、径向风道尺寸等相关因素进行了分析，通过计算分析可以得出以下结论:

1)通过对转子径向风道的分析可知，转子径向风道能起到等效风扇作用，使风道内压头有阶跃升高，随着电机转速的增加，转子径向风道的等效风扇作用加强，对于改善入口侧和中部风道的通风效果明显，对出口侧径向风道影响不大。

2)电机径向风道采用等宽度安装虽然工艺简单，但会使内部通风不均，呈现出两侧通风好，中间通风不良的情况，而采用改变供风路截面和径向风道不等距安装的手段可有效优化内部通风。

3)通过对转子温度场的分析可知，通风的不均衡分布将导致温度的不均衡分布。通过改变通风结构的尺寸能够有效改善通风效果，但换热性能的好坏要同时受到换热系数及温差两个因素的制约，在评价换热性能时应予以全面考虑。

4)集总参数的通风模型不受计算机硬件条件限制，可以有效用于计算电机整体流量流速分布。计算速度快，计算模型调整相对简单等优势利于其应用于通风的优化设计。

[1]丁舜年.大型电机的发热与冷却[M].北京:机械工业出版社，1992:112-133.

[2]魏永田，孟大伟，温嘉斌.电机内热交换[M].北京:机械工业出版社，1998:185-246.

[3]STATON D A，CAVAGNINO A.Convection heat transfer and flow calculations suitable for electric machines thermal models[J].IEEE Transactions on industrial electronics，2008，55(10):3509-3516.

[4]NONAKA S，YAMAMOTO M，NAKANO M，et al.Analysis of ventilation and cooling system for induction motors[J].IEEE Transactions on Power Apparatus and Systems，1981，PAS-100(11):4636-4642.

[5]SRINIVIS K N，ARUMUGAM R.An investigation into the air velocity distribution inside switched reluctance motors[J].Electric Power Components and Systems，2004，32(9):893-900.

[6]温嘉斌，鄢鸿羽.定子通风槽钢对通风沟内流体流动性太的影响[J].电机与控制学报，2010，14(11):58-62.WEN Jiabin，YAN Hongyu.Influence of stator ventilation channel of fluid flow pattern inside ventilation duct[J].Electric Machine and Control，2010，14(11):58-62.

[7]路义萍，郑国丽，丰帆，等.大型空冷汽轮发电机转子多种通风方案比较[J].电机与控制学报，2010，14(8):24-29.LU Yiping，ZHENG Guoli，FENG Fan，et al.Comparison of various ventilation proposals for a large air-cooled turbed-generator rotor[J].Electric Machine and Control，2010，14(8):24-29.

[8]路义萍，马贤好，李伟力.空冷汽轮发电机转子风道结构对传热的影响[J].中国电机工程学报，2007，27(17):61-66.LU Yiping，MA Xianhao，LI Weili.The effect of geometry factors on heat transfer of rotor’s cooling duct of large turbo generator with air-coolant[J].Proceeding of CSEE，2007，27(17):61-66.

[9]韩家德，马贤好，路义萍，等.汽轮发电机转子径向空气流量分布数值计算[J].中国电机工程学报，2007，27(32):73-76.HAN Jiade，MA Xianhao，LU Yiping，et al.Numerical calculation of air mass flow rate distribution in rotor[J].Proceeding of CSEE，2007，27(32):73-76.

[10]李伟力，靳慧勇，丁树业，等.大型同步发电机定子多元流场与表面散热系数数值计算与分析[J].中国电机工程学报，2005，25(32):138-143.LI Weili，JIN Huiyong，DING Shuye，et al.Numerical calculation and analysis of large synchronous generator stator multidimensional fluids and surface heat transfer coefficients[J].Proceeding of CSEE，2005，25(32):138-143.

[11]丁树业，李伟力，靳慧勇，等.发电机内部冷却气流状态对定子温度场的影响[J].中国电机工程学报，2006，26(3):131-135.DING Shuye，LI Weili，JIN Huiyong，et al.Cooling air state inside generator effect on stator temperature fields[J].Proceeding of CSEE，2006，26(3):131-135.

[12]RAJAGOAL M S.Finite element analysis of radial cooled rotating electrical machines[J].International Journal of Numerical Methods for Heat＆ Fluid Flow，1999，9(1):18-38.

[13]胡俊辉，许承千.大型异步电机通风的研究和计算[J].大电机技术，1992(6):25-29.HU Junhui，XU Chengqian.The ventilation study and calculation of medium and large induction generator[J].Large Electric Machine and Hydraulic Turbine，1992(6):25-29.

[14]黄立民，魏永田，陈季平，等.水轮发电机通风系统的网络矩阵计算[J].哈尔滨电工学院学报，1993，16(3):211-218.HUANG Limin，WEI Yongtian，CHEN Jiping，et al.The calculation of ventilation system in hydro-electric generator by network matrix approach[J].HIET Journal，1993，16(3):211-218.

[15]温嘉斌，孟大伟，鲁长滨.大型水轮发电机通风发热综合计算[J].中国电机工程学报，2000，20(11):6-9.WEN Jiabin，MENG Dawei，LU Changbin.Synthetic calculation for the ventilation and heating of large water wheel generator[J].Proceeding of CSEE，2000，20(11):6-9.

[16]温嘉斌，孟大伟，周美兰，等.大型水轮发电机通风发热场模拟研究及通风结构优化计算[J].电工技术学报，2000，15(6):1-4.WEN Jiabin，MENG Dawei，ZHOU Meilan，et al.Field model research of ventilation and heat optimal calculation of ventilation structure for large water wheel generator[J].Transactions of China Electrotechnical Society，2000，15(6):1-4.

[17]胡晓红，袁益超，刘聿拯，等.汽轮发电机转子径向通风系统冷却流量分配研究[J].机械工程学报，2010，46(14):139-142.HU Xiaohong，YUAN Yichao，LIU Yuzheng，et al.Study on the flow characteristics of radial ventilation in turbo-generator rotor[J].Journal of Mechanical Engineering，2010，46(14):138-142.

[18]迟速，李春廷，李梦启.水轮发电机通风系统的网络计算方法[J].黑龙江电力技术，1999，21(3):10-12.CHI Su，LI Chunting，LI Mengqi.The network calculation method of hydro-generator ventilation system[J].Heilongjiang Electric Power，1999，21(3):10-12.

[19]李玉柱，贺五洲.工程流体力学[M].北京:清华大学出版社，2006:69-104.