高效高压中型异步电机绝缘结构设计分析

孟大伟，姜明丽

(哈尔滨理工大学 电气与电子工程学院，黑龙江 哈尔滨150080)

0 引言

电机的重要技术经济指标之一是重量功率比，即kg/kW。减薄主绝缘可以提高槽利用率，从而达到减小重量功率比，减小电机体积和制造成本的目的[1]。以往多采用实验的方法减薄主绝缘[2]，而实验的方法不能直观的反映电场对主绝缘的作用。利用有限元方法对绝缘层电场进行分析计算，就可以获得绝缘层表面的电场分布情况[3－5]。在此基础上，来优化绝缘尺寸与结构，对于高效节能电机的研究具有重要意义。

本文以YKK400－6(690 kW)中型高压异步电机为参考样机，运用有限元方法对电机定子槽部电场、角部电场和端部电场进行计算分析，计算结果可以为定子主绝缘的减薄和优化结构提供理论依据。同时，通过介质损耗角正切实验和和瞬时工频击穿电压试验，验证了减薄后的绝缘厚度能够满足电机运行的需要。

1 定子槽部电场计算

电机绝缘结构中对电场的求解，可归纳为边值问题[6]，即

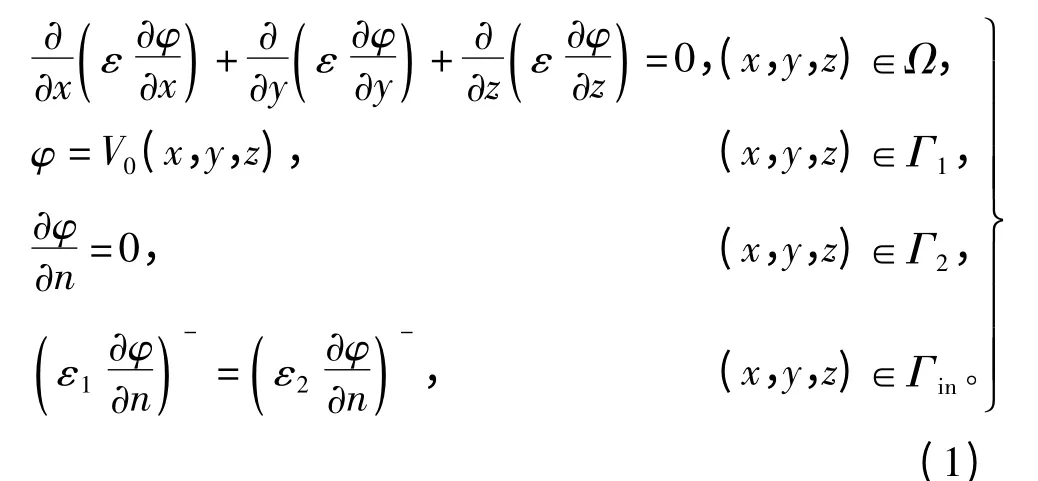
式中:Ω为定解场域;Γ1为电势已知的边界;Γ2为电势的法向导数等于零的边界;Γin为不同介质的分界线。

电机的槽部电场和角部电场可近似为二维场进行计算[7]，而端部由于其结构的复杂性，采用三维场进行计算。

1.1 定子槽部电场有限元数值方程

选用样机的额定电压为6 000 V，定子槽宽为11.9 mm，高为69.5 mm，层间绝缘厚为2 mm，主绝缘为1.5 mm。以定子槽宽度方向为x轴，高度方向为y轴，结合电机的实际尺寸建立计算模型。绝缘材料按均匀、线性、各向同性媒质处理，忽略槽楔对电场的影响，槽内间隙均按真空处理。计算模型如图1所示。

三相异步电机的外接电压按正弦规律变化，因此槽内上、下两层线圈在各个时刻的电位可以通过计算得到。电位沿轴向的梯度较小，可忽略不计。因此在任一时刻定子的槽部电场均可以当做二维静电场处理[8]。

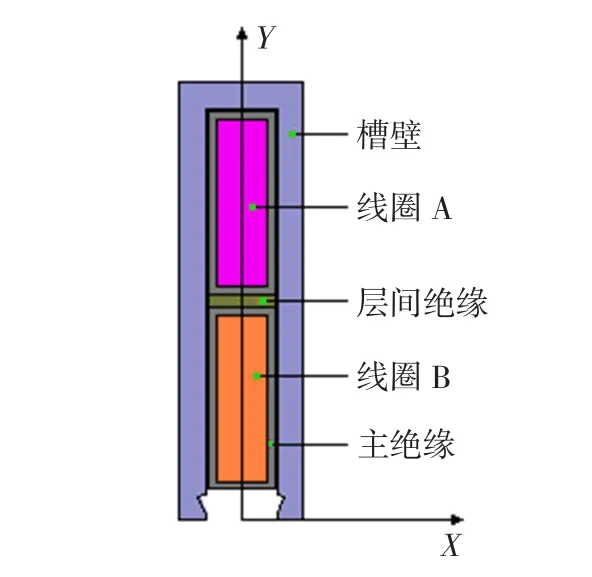
图1 定子槽部电场计算模型Fig.1 Calculating model of stator slot electric field

基于以上条件，标量电位φ满足的方程为

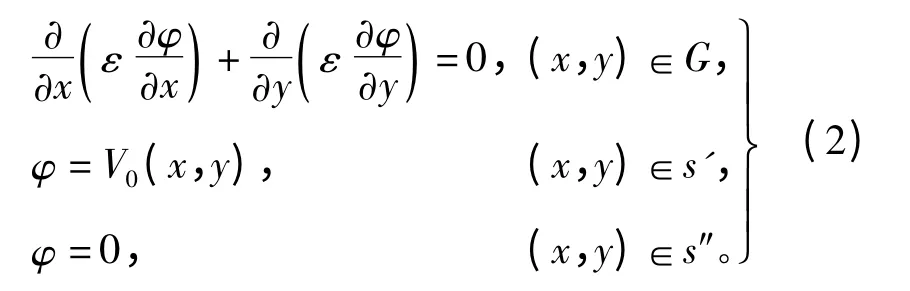
其中:ε为介质的介电常数;G为定解场域;s'为高电位面域(线圈导体);s″为零电位面。

由图1及槽型与绝缘尺寸可知，G满足范围为

{x∈[－5.95，5.95]，y∈[36，38]∪

y∈[67.5，69.5]}∪{y∈[5，69.5]，

x∈[－5.95，－4.2]∪x∈[4.2，5.95]}。

边界条件为:设定子槽壁表面电位为零，则s″满足范围

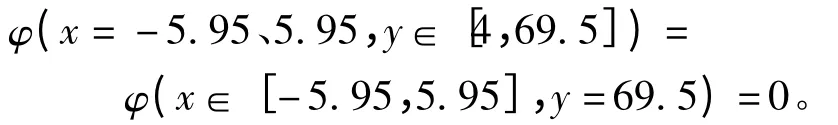
当A，B两线圈之间相位差为120°时，上下两层线圈之间的电位差变化最明显。以线圈A的坐标为基准，在A、B两线圈导体上加高电位，所加的电压为整机对地耐压试验所用电压值(17 kV)。即s'满足范围

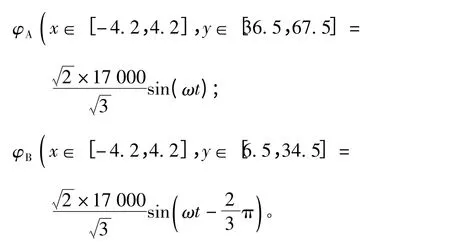
1.2 定子槽部电场计算结果

线圈A，B的电位差为

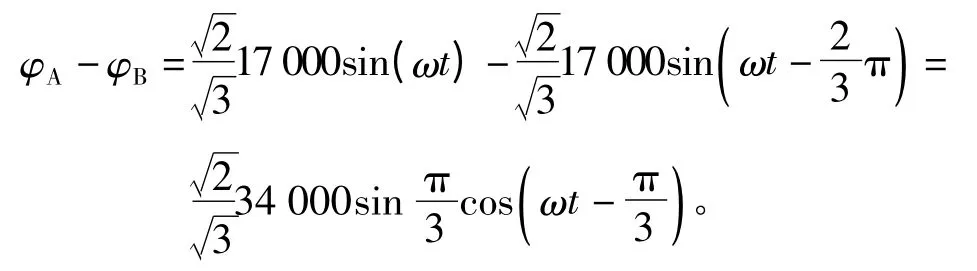
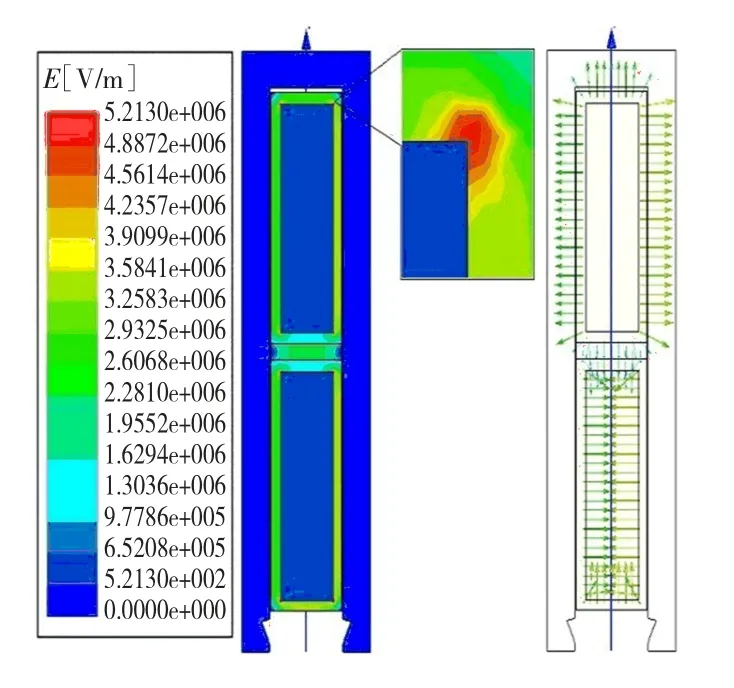
图2 时电场强度云图和矢量图Fig.2 Electric field intensity cloud picture and vector-graph withdegree

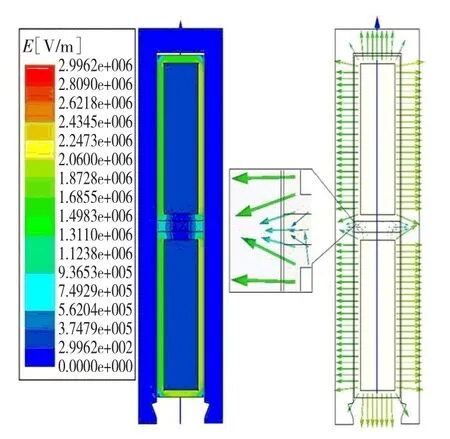
图3 时电场强度云图和矢量图Fig.3 Electric field intensity cloud picture and vector-graph with degree

观察图2、图3中电场分布，发现场强最大值出现在线圈尖角部分，即在线圈尖角部分出现了电场集中现象，在矩形线圈的四个侧面，电场分布是比较均匀的。分析发现线圈尖角部分的电场集中现象是由于导体几何形状突变所造成的，所以有必要对线圈角部进行结构优化。

2 线圈角部电场的计算

为了减小角部电场集中效应，通常把线圈的角部做成有一定圆角的形状，其截面简化模型如图4所示。

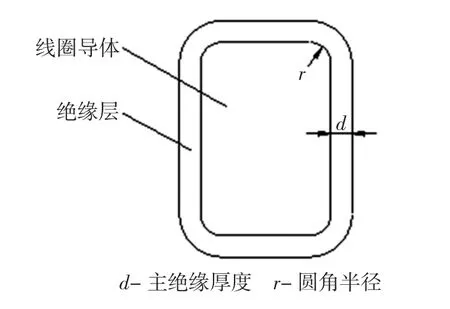
图4 带圆角的截面简化模型Fig.4 Simplified section model with rounded corners

线圈的4个角部是对称的，即可以选择线圈截面的四分之一进行分析。建立主绝缘厚度为d=1.5 mm，半径r=1.8 mm的计算模型。对线圈加载时的整机对地耐压试验所用电压的瞬时值，绝缘层外侧为零电位边界。应用静电场求解器进行计算，计算结果如图5所示。E[V/m]

1.2925 e+007 1.2117e+007 1.1310e+007 1.0502e+007 9.6942e+006 8.8864e+006 8.0787e+006 7.2710e+006 6.4632e+006 5.6555e+006 4.8477e+006 4.0400e+006 3.2323e+006 2.4245e+006 1.6168e+005 8.0903e+005 1.2925e+003

观察图2和图5的放大部分，由于采用了圆角结构，角部电场分布变得均匀，最大电场强度由原来的1.757×107V/m下降为1.293×107V/m。根据经验公式[9]

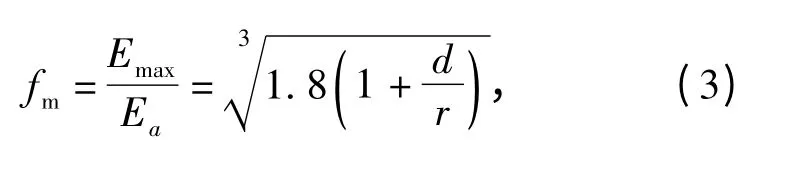
图5 圆角结构的角部电场云图Fig.5 Electric field intensity cloud picture in rounded corner

式中:fm为电场集中系数，Ea为平均场强，d为主绝缘厚度，r为圆角半径，Emax为最大电场强度，由

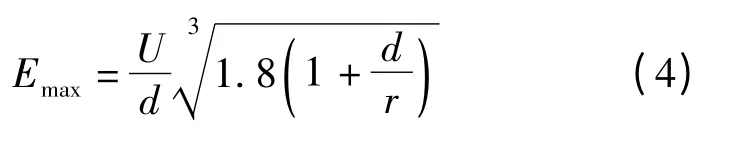
确定。可知，欲改善定子线圈的电场分布，需减小电场集中系数 fm，而要减小 fm，就必须降低 d/r的值。

改变d和r的值，建立计算模型。对各模型中线圈导体加载整机对地耐压试验所用电压值，设绝缘层外侧为零电位边界，采用静电场求解器进行计算。若在此电压值下绝缘能满足要求，则主绝缘可以保证电机的安全运行。

通过计算，得到d和r取不同值时的电场分布，取最大电场强度进行对比，如图6所示。

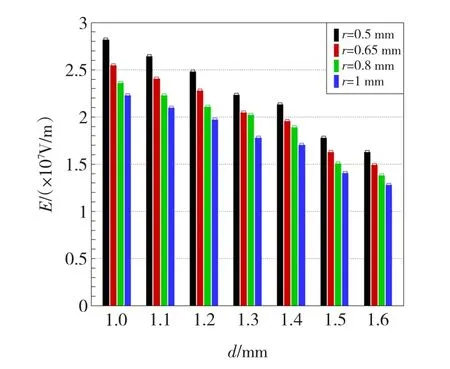
图6 d和r 取不同值时最大电场强度Fig.6 Maximum electric field intensities with different d and r

从图6中可观察到当绝缘厚度相同时，最大电场强度的值随圆角半径的增大而减小;当圆角半径相同时，最大电场强度值随绝缘厚度的增大而减小。其中1.5 mm为原绝缘结构、1.1 mm为所确定的新绝缘结构。

3月6日上午，1 6 1师战地医院装车回国，殷燕坐车从友谊关回到了广西。殷燕记录了自己入关回国的心绪：“从友谊关经过的军人们，无不被那楼顶上迎风飘扬的五星红旗所吸引，那深情凝望的眼神，是经受过战场考验、从生死线上走回来的人才会有的，那是发自心底对祖国依恋的神情。军人们就像久别了母亲的孩子一样，禁不住热泪盈眶，面对着国旗，举起右手久久地行着军礼不愿放下。”

由图5可知主绝缘电场强度的最大值与最小值均出现在角部45°射线方向上。在1.5 mm和1.1 mm绝缘的各模型沿角部45°方向做射线，分别提取该线上节点的电场强度作对比分析，如图7所示。计算该线上节点电场强度的平均值，其值可作为平均场强Ea。根据图6中的最大值就可以求得电场集中系数fm。图8为fm与r和d的关系。分析可知当绝缘厚度一定时，圆角半径越大fm越小。在满足绝缘结构的要求情况下，考虑提高槽利用率和生产工艺两方面，选择0.8 mm的圆角半径为宜。

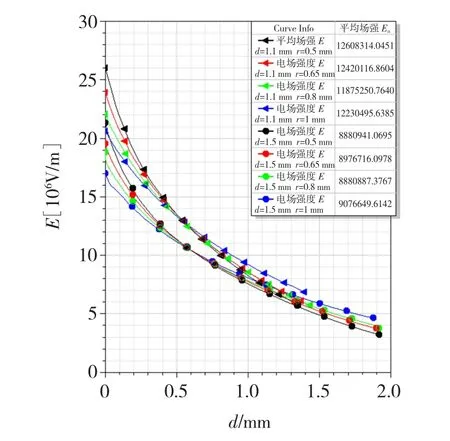
图7 角部45°射线上电场分布图Fig.7 The electric field distribution along radial direction with 45°

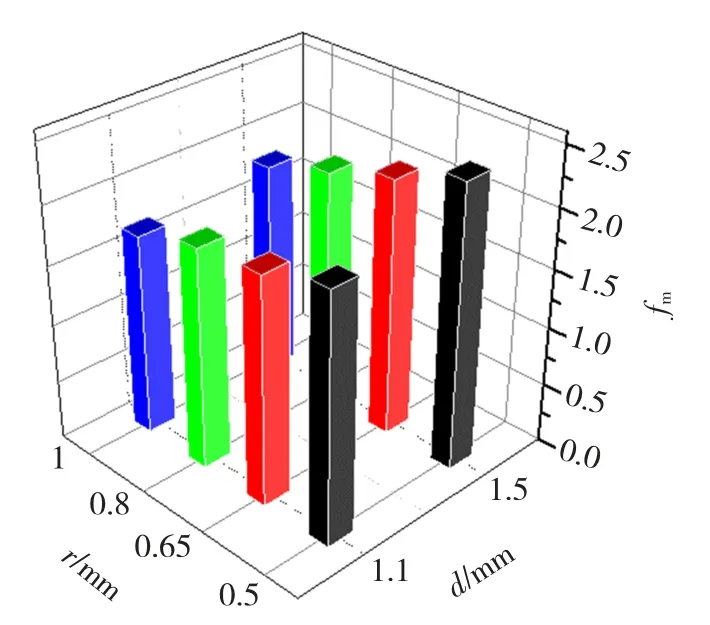
图8 不同r和d下的fm值Fig.8 fm values with differentrandd

3 定子绕组端部电场计算

定子绕组端部几何形状复杂，在形状突变处电场分布极不均匀，容易产生绝缘损坏现象，需对端部电场分布进行分析。

根据电机定子绕组端部实际尺寸进行建模，模型和网格划分如图9所示。槽部主绝缘厚度为1.5 mm时，端部绝缘厚度为1.65 mm。当槽部主绝缘厚度减薄为1.1 mm时，端部采用1.45 mm厚的绝缘结构。对定子绕组端部线圈导体加载整机实验线电压值(17 000 V)，设绝缘层外表面为零电位边界。

图9 定子绕组端部模型和剖分图Fig.9 Stator end winding model and mesh grid

计算结果如图10所示，其中(a)为端部绝缘1.65 mm的结构，(b)为端部绝缘1.45 mm的结构。

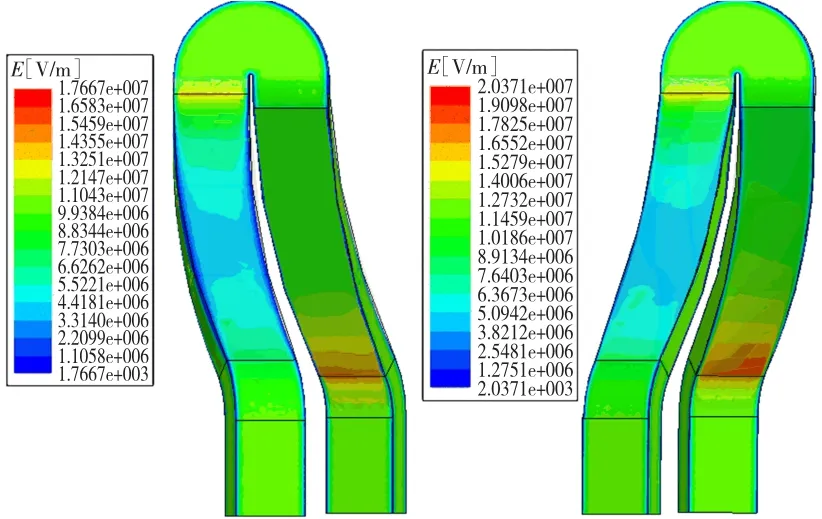
图10 绕组端部电场计算云图Fig.10 Electric field intensity cloud in end winding

减薄后端部电场强度最大值为2.0371×107V/m，完全满足绝缘要求，并保留一定的安全裕度。

4 绝缘性能试验

以电场计算的结果作为参考，按JB/T 50132－1999标准对定子主绝缘厚度为1.5 mm和1.1 mm的线圈进行常态下介质损耗角正切、热态介质损耗角正切和瞬时工频击穿电压试验。

实验结果如图11和表1所示。

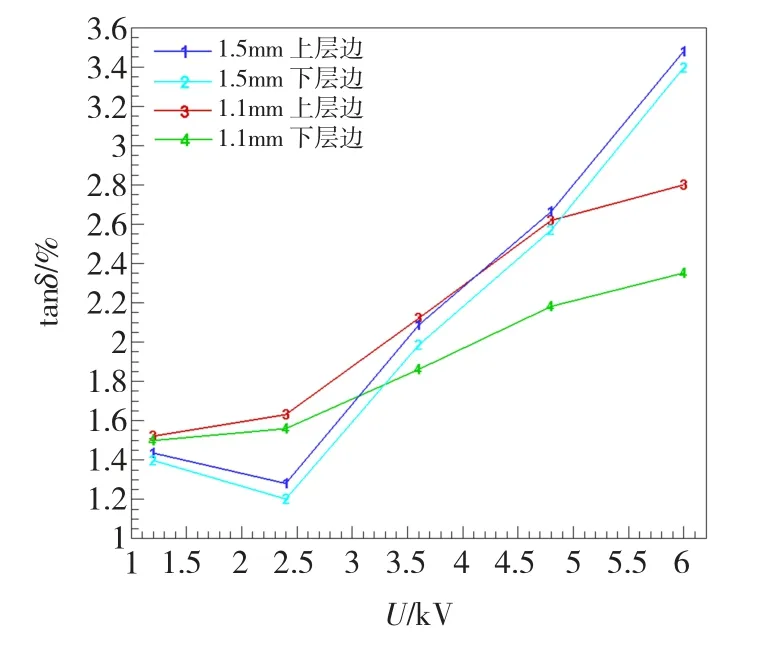
图11 常态下不同绝缘厚度线圈的tanδ(%)Fig.11 tanδ(%)values of the windings with different insulation thickness in the normality

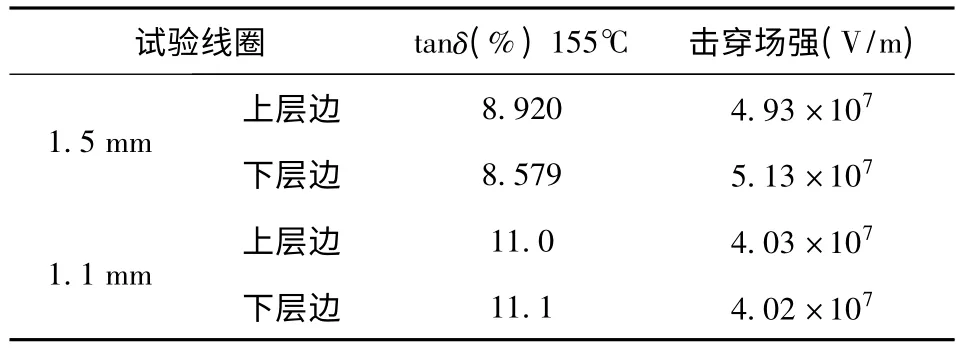
表1 不同绝缘厚度线圈的热态介损与击穿电压Table 1 Thermal dielectric losses and breakdown voltages of the windings with different insulation thickness

5 结论

总结计算结果和试验结果，可得以下几点结论:

1)为了改善线圈电场的分布，在设计绝缘结构时，须采用合理的圆角半径。兼顾提高槽利用率和减小电场集中系数两个指标，线圈截面的圆角半径选择0.8 mm比较适宜。

2)绝缘厚度为1.1 mm的试验线圈采用高介电性能的少胶云母带和优化结构，与原结构1.5 mm的试验线圈相比，绝缘结构满足要求。

3)当槽部绝缘减薄为1.1 mm时，端部端部建议采用1.45 mm的绝缘厚度。由于端部所处位置决定其电场分布沿绝缘表面存在着较强的切向和垂直的分量，且电晕强烈。在满足槽部绝缘要求时，端部不易过度减薄，要保证电机的安全性能。

本文采用整机试验电压进行计算，与线圈击穿试验对比，各处计算电场强度均没有超过击穿场强。当电机在额定电压下工作时，优化的绝缘结构能够保证电机的安全可靠运行。

[1]赵慧春.高压电机定子线棒绝缘结构设计及其性能研究[D].哈尔滨:哈尔滨理工大学材料科学与工程学院，2008.

[2]侯力，梁茂芝，王艳萍.大型水轮发电机定子线棒绝缘厚度减薄研究[J].防爆电机，2004，3:24 －28.HOU Li，LIANG Maozhi，WANG Yangping.Study on thinning of insulstion thickess of stator bars in large-Sized Hydraulic generator[J].Explosion-Proof Electric Machine，2004(3):24 － 28.

[3]PIHLER J，TICAR I.Design of systems of covered overhead conductors by means of electric field calculation[J].IEEE Transaction on Power Delivery，2005，20(2):807 －814.

[4]LIN Li，FENG Ji，GANG Liu，et al.Calculation of transient electric field of converter transformer under polarity reversal voltage[C]//Electromagnetic Field Computation(CEFC).2010:735－736.

[5]QI Hongwei，ZHOU Dan.Influence of shields to the static electric field in vacuum interrupter for optimization designing[C]//Control and Decision Conference，2009，June 17 － 19，2009，Guilin，China.2009:1973 －1977.

[6]汤蕴璆.电机内的电磁场[M].北京:科学出版社，1998.E[V/m]1.7667e+007 1.6583e+007 1.5459e+007 1.4355e+007 1.3251e+007 1.2147e+007 1.1043e+007 9.9384e+006 8.8344e+006 7.7303e+006 6.6262e+006 5.5221e+006 4.4181e+006 3.3140e+006 2.2099e+006 1.1058e+006 1.7667e+003

[7]姜刚，刘念，肖玲，等.基于电磁场有限元方法的大型发电机定子槽绝缘故障诊断分析[J].四川电力技术，2008，31(5):53－55.JIANG Gang，LIU Nian，XIAO ling，et al.Analysis and diagnosis the generator stator slot insulation fault based on the finite element method of the electromagnetic field[J].Sichuan Electric Power Technology，2008，31(5):53 －55.

[8]马山刚，李钊年，王佐亮.基于ANSYS的高压电机定子槽电场有限元仿真分析[J].青海大学学报，2009，27(6):20 －22.MA Shanggang，LI Zhaonian，WANG Zuoliang，et al.Finite element simulation analysis of electric field of high-voltage generator stator slot based on ANSYS[J].Journal of Qinghai University.2009，27(6):20 －22.

[9]隋银德，傅岚贵.高压电机定子线圈电场分布的改善[J].大电机技术，2001(2):22－25.SUI Yingde，FU Langui.Improvement of electric field distribution of stator coil for HV electric machinery[J].DA DIANJI JISHU，2001(2):22－25.

[10]严璋，朱德恒.高电压绝缘技术[M].北京:中国电力出版社，2007.