基于数值微分方法的卫星陀螺故障诊断
王振华,沈 毅,张筱磊
(哈尔滨工业大学航天学院,哈尔滨150001)
0 Introduction
The gyroscope is one of the primary attitude determination sensors used to measure the attitude angular rate of satellite with respective to the inertial reference coordinate system,its reliability is critical to the safety and performance of a satellite.Although gyroscopes are designed with high reliability,faults are prone to occur due to the harsh on-orbit environment.
Fault diagnosis can be used to increase the safety and reliability of gyroscopes in satellite.Traditionally,health monitoring for the gyroscope is achieved by measuring and processing some internal variables,such as temperature,current,and voltage and so on.These methods are easy to understand and implement.However,their performance is limited.It is known that there are some redundant gyroscopes equipped in many modern satellites.Therefore,the fault detection and isolation can be achieved by voting or parity check methods.However,too many sensors will lead to high cost,large space,and additional weight[1].
In fact,the attitude kinematics equations provide us an analytical relation,which can be used to design the model-based fault diagnosis method.In papers[2-3],F.N.Pirmoradi et al.studied the fault diagnosis methods for attitude sensors based on satellite dynamics and kinematics equations.In[4],the attitude kinematics equation is used to design an observer-based fault detection and isolation scheme.These results are mainly designed to detect the presence of failure and identify the faulty component.However,they can not provide any information about the magnitude of the fault[5].In fact,fault estimation(or fault reconstruction)is one of the most important processes in a fault diagnosis scheme.
Most recently,Diop et al.proposed an appealing fault diagnosis method based on the numerical differentiation scheme[6-8].Its main idea is to transform the fault diagnosis problem as numerical differentiation.The advantages of the fault diagnosis approaches based on numerical differentiation lie in the flexibility and intuitiveness.Such methods can estimate the magnitude of the fault whenever the algebraic observable condition is satisfied.
Motivated by the work of Diop et al,this paper reformulates the fault diagnosis problem to numerical differentiation based on a bank of high gain observers.Using the attitude kinematics and the measurement provided by attitude sensors,the presented method is capable of reconstructing the gyroscope fault directly.The remainder of this paper is organized as follows.First,the algebraic observability of the fault is introduced,and then it is proved that the gyroscope fault is algebraic observable.Next,the numerical differentiation using high gain observer is described.And then the fault diagnosis approach is developed based on the algebraic observability and numerical differentiation scheme.Finally,a couple of simulation results are given to illustrate the performance of the proposed fault diagnosis method.
1 Problem formulation
The unit quaternion is used to describe the attitude of the satellite for global representation without singularities.Quaternion is a four-dimensional vector in the following form
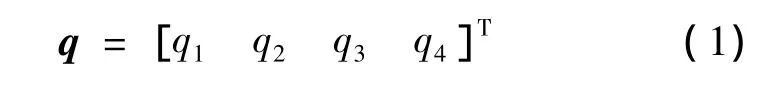
Quaternion satisfies the normalization constraint

It should be noted that only the gyroscopes fault is considered in this paper and the output of gyroscopes is modeled by

whereωgis the output of gyroscopes,ωrepresents the angular velocity vector of the body frame with respective to the inertial coordinate frame,and f(t)denotes the unknown fault function.
In order to reconstruct the fault of gyroscope sensors by numerical differentiation method,the definition of algebraic observable is first given here[7-9].
Definition 1:(Algebraic Observable)The fault vector f(t)is algebraic observable if each component fi(t)satisfies the following algebraic relationship
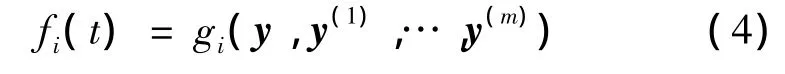
where gi(·)is a known smooth map,y is a known vector,and y(m)represents the m th derivative of y,with m is a finite positive integer.
The following theorem is proposed based on the definition of algebraic observable.
Theorem 1.Given the attitude quaternion q,then the fault of gyroscopes f(t)is algebraic observable.
Proof.The quaternion kinematics equation is given by

where
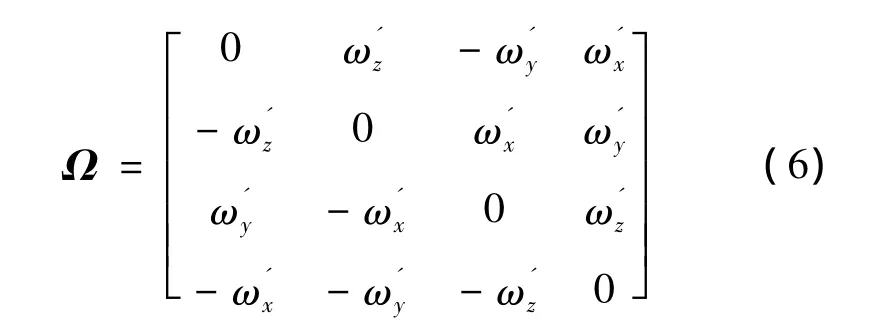
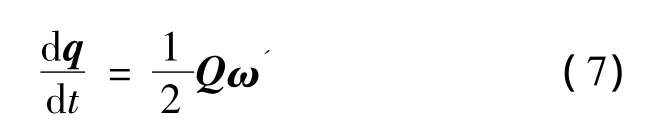
where
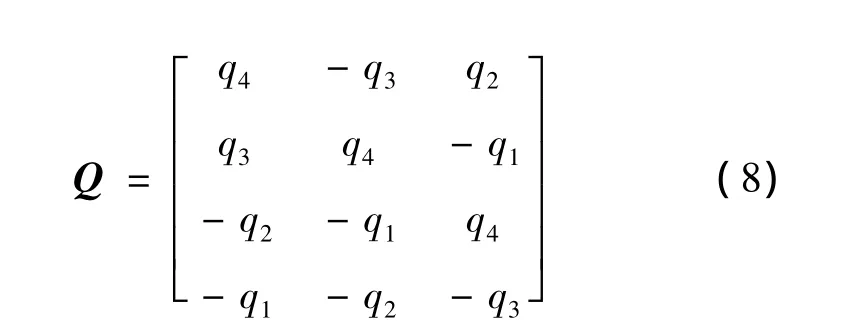
Using the prosperity of unit quaternion,we have

Using the equations(7)and(9),results in
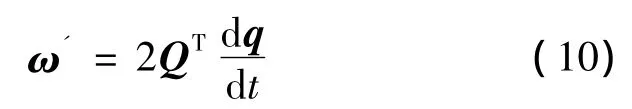
Then the angular velocityωis obtained as

whereωois the orbital rate of the satellite,A(q)is the transformation matrix from inertial frame to the orbital frame.
Substituting equation(11)into(10),yields

Using(3)and(12),we have
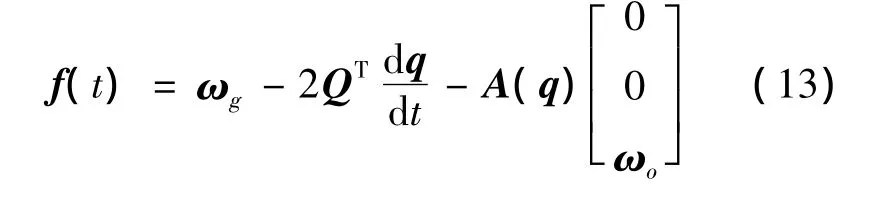
As the vectorsωgand q are known,f(t)can be expressed as the function ofωg,q,andTherefore,f(t)is algebraic observable.
From Theorem 1,it can be concluded that if the attitude quaternion q and its time derivativeis available,f(t)will be obtained directly by using equation(13).Now the main difficulty lies in how to estimateThis is to say,the fault estimation is transformed as a numerical differentiation problem,which can be solved by several methods,such as backward difference[11-12],polynomial interpolation method[6],high-order sliding mode differentiator[13-14],numerical differentiator using high gain observer[15-16],and so on.Among these methods,the numerical scheme using high gain observer is easy to design and implement.Therefore,this paper uses high gain observers to achieve the numerical differentiation.
2 Numerical differentiation based on the high gain observer
Before designing a high gain observer to obtain numerical differentiation,the numerical differentiation problem is formulated as the following form

where x=[x1x2]Tis the state vector,y∈R is a signal to be differentiated,v∈R represents the measurement noise.x1∈R is the estimation of y,x2∈R and u∈R are the time derivatives of x1and x2,respectively.It should be noted that variables x1,x2,and u are unknown.
In equation(14),the matrices A,B,and C are given as
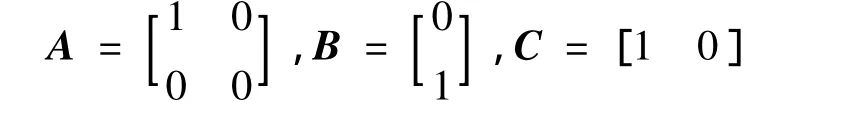
In addition,the following assumptions are considered.
A1.y is continuously differentiable,and u is bounded,with
A2.The measurement noise v is bounded with
The high gain observer has the form
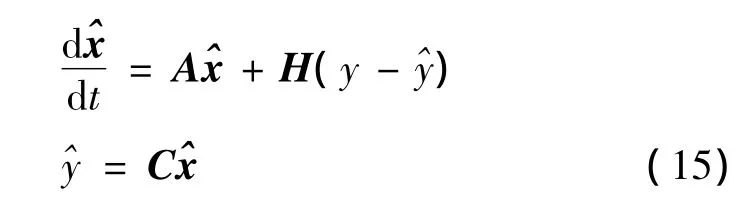
where the observer gain matrix H is given by
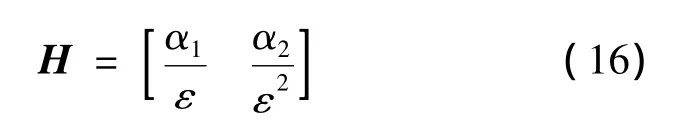
withεis a small positive parameter to be designed,and the roots of
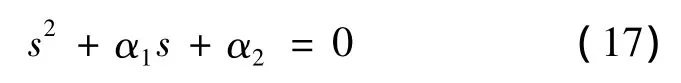
have negative real parts.
Define the estimation error as

and for the purpose of analysis,the scaled estimation error is considered

where

Subtracting(15)from(14),the dynamics of the scaled estimation error is derived and written as
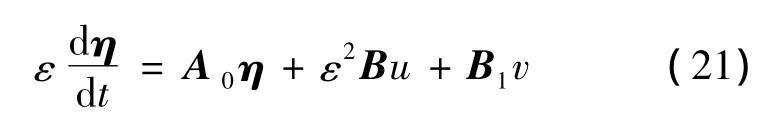
where
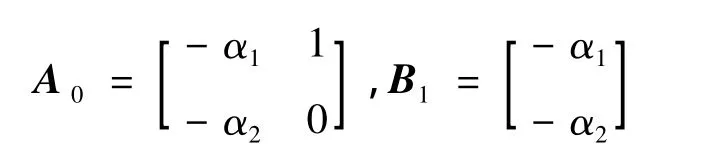
From equation(17),the matrix A0is Hurwitz[15].
The positive parameterεin the observer(15)is designed by the following theorem.
Theorem 2.Let the assumption A1 and A2 holds,the estimation error of high gain observer(15)is bounded as follows
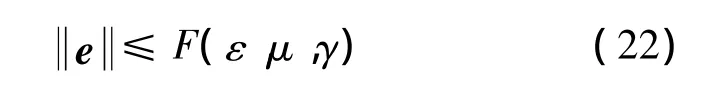
with
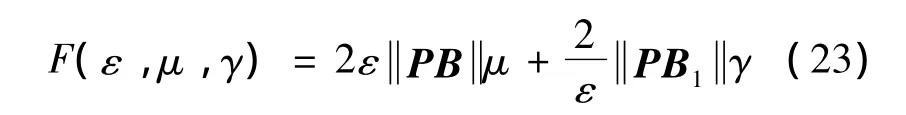
where a denotes the Euclidean norm of a vector a,and X represents the induced two-norm of a matrix X.
Proof.Taking V(η)=ηTPηas a Lyapunov function candidate for(21),where P is a definite symmetric matrix which is the solution of
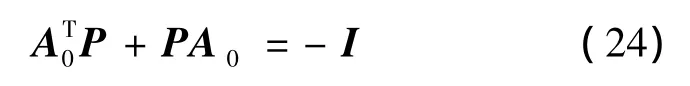
The time derivative of V(η)is given as
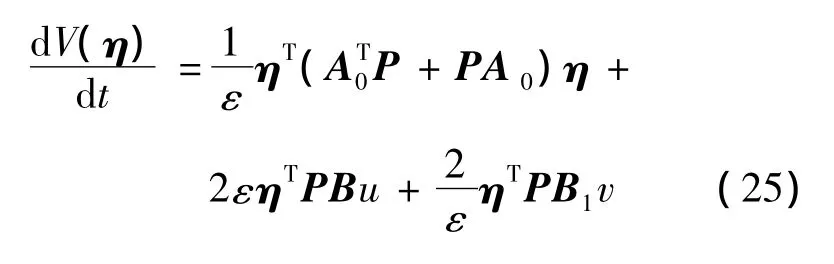
Using the assumption A1,we have
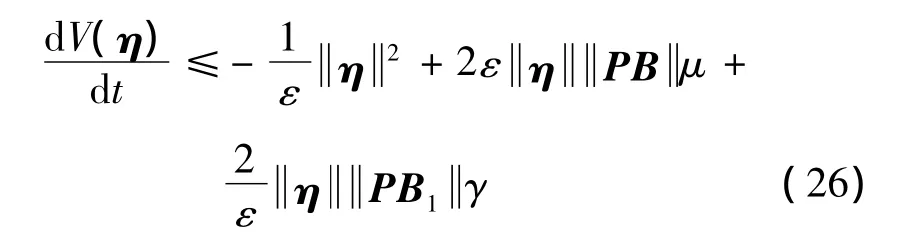
Then
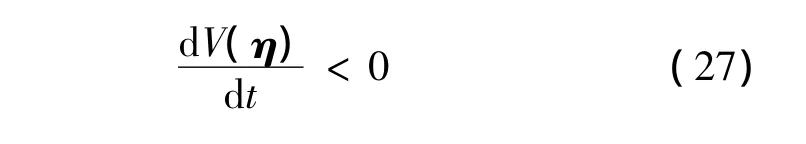
for
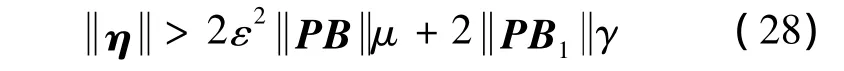
Hence the set
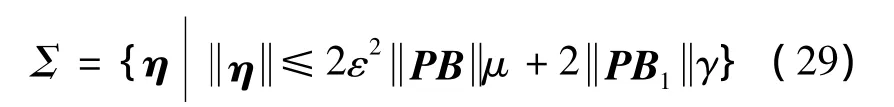
is positively invariant,i.e.ifηis outsideΣ,it will decease to reach the setΣ,andηwill be bounded,if it is insideΣ.According to the definition of scaled estimation error,we have
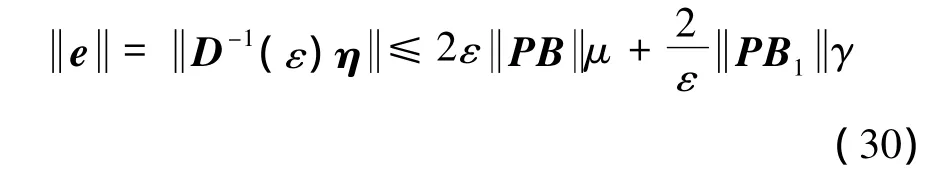
i.e.
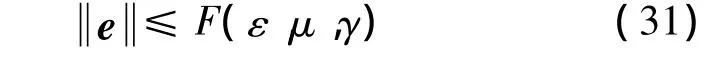
This completes the proof.
From(31),it can be seen that the estimation error e is ultimately bounded.However,the observer parameterεcannot be chosen arbitrarily small,a tradeoff must be considered due to the unknown function u,and measurement noise v.
In this paper,εis designed by minimizing bound of the estimate error,F(ε,μ,γ).Similar to the Lemma 1 in[16],it can be shown that F(ε,μ,γ)has minimum at
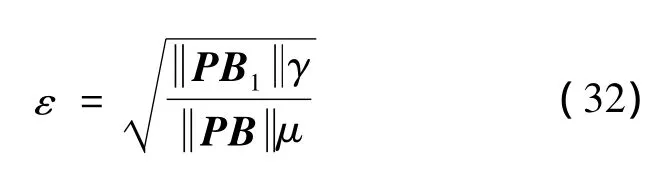
In fact,such a compromise makes the proposed high gain observer act as a filter.It can calculate the numerical differentiation with the ability of attenuation to the measurement noise.
Now,since the attitude quaternion q is measured by the attitude sensors and its numerical differentiation can be provided with high gain observers,we can resort to equation(13)to estimate the fault of gyroscope sensors.The fault diagnosis scheme is given by
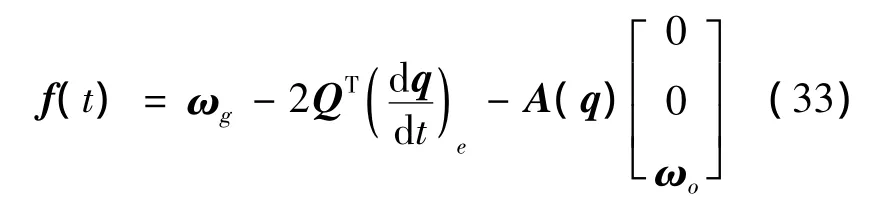
whereωois available,ωgand q are measurements given by gyroscopes and attitude sensors,respectively.is the estimate of derivative of q provided by the high gain observers.
3 Simulations
In this section,numerical simulations are given to illustrate the effectiveness of the proposed fault diagnosis method.In the simulation,the gyroscope noise standard deviation,and the attitude vector noise standard deviation are set toσg=0.005°/s,andσs=0.05°,respectively.The specifications ofμandγare taken asμ=0.05,andγ=5×10-4.The parameters α1,α2in(17)are chosen asα1=1,α2=2.5.Solving the algebraic Riccati equation(24),gives
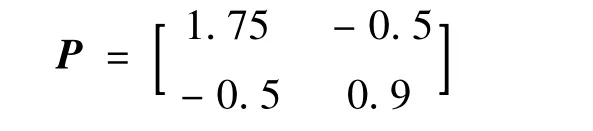
And then using equation(32),we obtainε=0.133.
The performance of the proposed fault diagnosis scheme for three different fault scenarios are described below and the results are analyzed.In order to illustrate the advantage of the proposed method,the fault diagnosis procedure is also carried out via the backward difference differentiators.
First,consider there is a struck-up fault with the pitch gyroscope from t=10s.In other words,the measurement output of the pitch gyro is a constant.
The simulation result is shown in Fig.1.Therein,the gyroscope faults are represented by the dashed curves while the fault estimates given by the proposed method is illustrated by the solid curves,and the dotted curves denotes the fault estimates provided by the fault diagnosis scheme using backward difference differentiators.It can be easily seen that the proposed approach can accurately reconstruct the faults within less than 1s.Moreover,the influence of the measurement noises is effectively decreased by the proposed method.
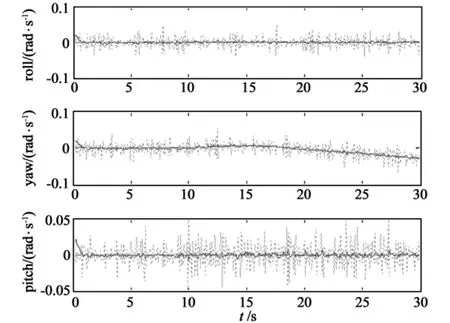
Fig.1 The fault estimation results of three-axis gyroscopes when there is a struck-up fault
Now the abrupt bias fault scenario is used to verify the effectiveness of the proposed method.Consider there is a fault with the roll gyroscope in t=20s,its magnitude is 2°/s.The simulation result is given as Fig.2.Therein dashed curves,solid curves,and the dotted curves illustrate respectively the gyroscope faults,the fault estimates given by the proposed method,and the fault estimates using the backward difference differentiators.As is shown,the presented method is also effective in this situation.
It should be noted that the proposed method can also be applied to reconstruct simultaneous faults.Consider both the gyroscopes in pitch axis and yaw axis are struck from t=15s.The simulation result is illustrated in Fig.3.
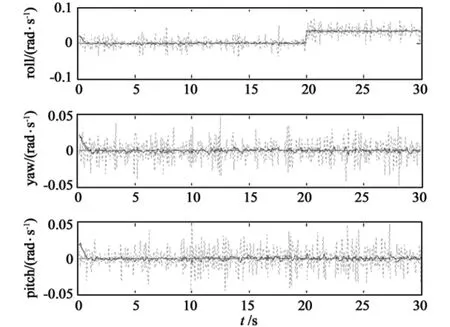
Fig.2 The fault estimation results of three-axis gyroscopes when there is an abrupt fault
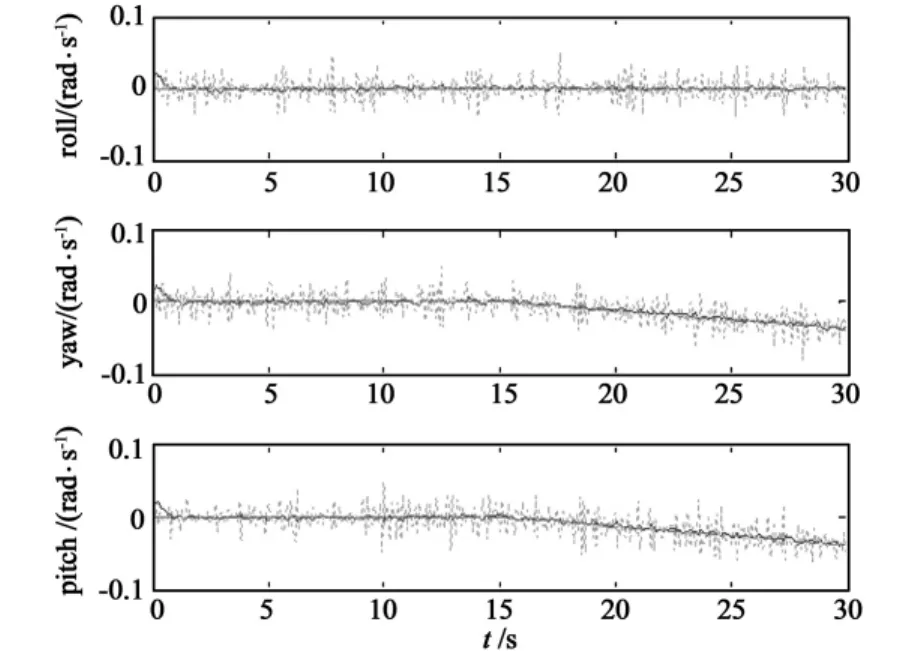
Fig.3 The fault estimation results of three-axis gyroscopes when there are multiple faults
In the above simulations,the estimation ability of the fault diagnosis method based on numerical differentiation has been verified by using abrupt,incipient,and simultaneous faults,respectively.The results show that the presented method can estimate the magnitude of the gyroscope fault accurately in different scenarios.
4 Conclusions
This paper presents a fault diagnosis approach based on numerical differentiation using high gain observer.In this work,high gain observer is used to approximate the derivatives of signals.And then the fault vector is reconstructed based on the numerical differentiation.The proposed method has the advantages of both fault detection and reconstruction.Simulation results confirm the effectiveness of the fault diagnosis method.In the future work,how to improve the performance of the numerical differentiator based on the high gain observer will be considered.
[1]Li Z,Liu G,Zhang R,et al.Fault detection,identification and reconstruction for gyroscope in satellite based on independent component analysis[J].Acta Astronautica,2011,68(7-8):1015-1023.
[2]Pirmoradi F N,Sassani F,Silva C W.An efficient algorithm for health monitoring and fault diagnosis in a spacecraft attitude determination system[C].IEEE International Conference on Systems,Man and Cybernetics,Montreal,Quebec,Canada,2007.
[3]Pirmoradi F N,Sassani F,Silva C W.Fault detection and diagnosis in a spacecraft attitude determination system[J].Acta Astronautica,2009,65(5-6):710-729.
[4]Venkateswaran N,Siva M S,Goel P S.Analytical redundancy based fault detection of gyroscopes in spacecraft applications[J].Acta Astronautica,2002,50(9):535-545.
[5]Gao Z,Ding S X.Sensor fault reconstruction and sensor compensation for a class of nonlinear state-space systems via a descriptor system approach[J].IET Control Theory and Application,2007,1(3):578-585.
[6]Diop S,Grizzle J W,Moral P E,et al.Interpolation and numerical differentiation for observer design[C].American Control Conference,Baltimore,Maryland,USA,1994.
[7]Diop S,Martinez-Guerra R.On an algebraic and differential approach of nonlinear systems diagnosis[C].The 40th IEEE Conference on Decision and Control,Orlando,Florida,USA,2000.
[8]Chen W,Saif M.High-order Sliding-mode differentiator based actuator fault diagnosis for linear systems with arbitrary relative degree and unmatched unknown inputs[C].The 45th IEEE Conference on Decision and Control,San Diego,CA,USA,2006.
[9]Fliess M,Join C,Sira-Ramirez H.Non-linear estimation is easy[J].International Journal of Modeling Identification and Control,2008,4(1):12-27.
[10]Sidi M J.Spacecraft dynamics and control:A practical engineering approach[M].New York:Cambridge University Press,1997:88-111.
[11]Mathews J H,Fink K D.Numerical methods using MATLAB(3rd)[M].Englewood Cliffs:Prentice Hall,1999:310-342.
[12]Tseng C,Lee S.Design of digital differentiator using difference formula and Richardson extrapolation[J].IET Signal Processing,2008,2(2):177-188.
[13]Levant A.High-order sliding modes:differentiation and outputfeedback control[J].International Journal of Control,2003,76(9-10):924-941.
[14]Iqbal M,Bhatti A I,Ayubi S I,et al.Robust parameter estimation of nonlinear systems using sliding-mode differentiator observer[J].IEEE Transaction on Industrial Electronics,2011,58(2):680-689.
[15]Dabroom A M,Khalil H K.Discrete-time implementation of high-gain observers for numerical differentiation[J].International Journal of Control,1999,72(17):1523-1537.
[16]Jeffrey H A,Khalil H K.High-gain observers in the presence of measurement noise:a switched-gain approach[J].Automatica,2009,45(4):936-943.
- 宇航学报的其它文章
- 基于在线轨迹规划的混合再入制导方法

