Dtrie-allpair:高效的集合T-覆盖连接算法*
贾连印 奚建清 李孟娟 游进国 刘勇 苗德成
(1.华南理工大学计算机科学与工程学院,广东广州510006;2.云南师范大学图书馆,云南昆明650092;3.昆明理工大学信息工程与自动化学院,云南昆明650500)
集合一直是研究者研究的热点,在众多涉及集合的问题中,集合相似度连接问题旨在从大量的集合中查找满足特定相似度阈值的集合对.该问题广泛存在于数据清洗[1-2]、近似重复判断[3]、抄袭检测[4]等领域.
需要注意的是,集合相似度连接问题不同于集合相似度查询问题[5].集合相似度查询算法通常基于全部数据构建静态的索引结构,同样可用于实现集合相似度连接算法.但高效的集合相似度连接算法为了避免出现重复的结果对而通常在部分数据基础上以动态递增的方式构建索引,因此具有更优的性能.
集合相似度问题同样不同于被广泛研究的集合包含问题[6-11].集合包含问题通常以集合包含查询为基础,可分为子集查询、超级查询和等值查询.集合包含查询通常用于查询一个集合完全包含或包含于另一个集合.而集合相似度查询或连接则着重于研究集合之间包含的程度.
近年来,研究者提出了多种不同的算法来解决集合相似性连接问题,例如算法 SSJoin[1]、PARTENUM 算法[2]、WTENUM 算法[2]、topk-join 算法[12]、MergeOpt算法[13]等.
众多算法中,Bayardo等[14]提出的 All-pair算法、Xiao等[3]提出的 PPJoin算法具有良好的伸缩性,能非常高效地扩展到上百万记录的All-pair问题的计算.
然而,这类算法通常基于反向索引结构并且基于生成-测试的框架来执行.它们首先在生成阶段生成候选集,然后在测试阶段对候选集进行逐一验证,从而得到最终的结果.当生成的候选集非常大时,系统的性能不可避免地会降低.为了解决这个问题,文中设计了一种动态trie索引结构——DTI结构,DTI采用流的思想根据已读入的记录动态地创建trie索引;在DTI基础上,文中提出了高效的Dtrie-allpair算法,并通过实例模拟对该算法进行了验证.
Trie-Join算法[15]同样基于trie结构研究集合相似度连接问题,然而该算法主要关注于编辑距离谓词,Dtrie-allpair则关注于T-覆盖谓词.T-覆盖更具有一般性,能用于解决其它相似度谓词.
1 相关定义
记录集:有限记录的集合称为记录集.
元素频率:指一个元素在整个数据库中出现的次数.
序:指记录或元素在数据库中出现的相对顺序.可分为元素序(元素在记录中的顺序)和记录序(记录在数据库中的顺序)两种.
常见的元素序有值序和频率序两种.值序是指按照元素大小安排元素在记录中的顺序,分为值升序和值降序;频率序是指按元素频率安排元素在记录中的顺序,分为频率升序和频率降序.
常见的记录序为长度序.所谓长度序,是指按照记录中元素数量安排记录在数据库中的顺序,分为长度升序和长度降序.
文中假设集合中元素为整型且不是多重集,即集合中不含重复元素.
本研究主要关注T-覆盖连接,它可用于解决其它相似度谓词的连接问题,如JACCARD、COSINE、DICE等,也是研究集合相似度连接的基础.下面给出T-覆盖连接的正式定义.
定义1 T-覆盖连接:给定两个记录集X和Y以及一个覆盖阈值T,找出所有<x,y>对(x∈X且y∈Y),使得x和y至少拥有T个公共元素(同时在记录x和y中出现的元素).即
文中着重于自连接,即记录集X=Y的情况,但本研究的工作可扩展到X≠Y的情况.
2 传统的T-覆盖算法
2.1 All-pair算法
All-pair算法是一种基于反向索引的算法,在MergeOpt算法[13]基础上发展而来,采用生成-测试的框架来执行.该算法采用流的思想,对每一个到来的记录x,通过索引探测已看到的每一个记录y,比较其是否与x有足够的相似度.为了检测x和y的相似度,只需对y的部分记录构建索引即可.为了确定y中需要索引的长度,该算法基于以下定理.
证明 由x的T-1个后缀和y的T-1个后缀最多有T-1个公共元素易见定理1成立.
因此,为了确定记录x和记录y是否有足够的相似度,该算法只需为y的个前缀元素建立反向索引即可.
在查找记录x的相似对之前,用x的每一个前缀元素p去探测由在x之前出现的所有记录的前缀建立的反向索引,p所对应的反向列表中的每一个记录y'可被看作与x相似的一个候选记录.
为了检测x和其任一候选记录y'的覆盖,该算法需要执行一个验证阶段来检测x和y'的实际覆盖值.
为了提高效率,All-pair算法引入了长度过滤机制,如果,则y'不可能成为x的候选集.该算法要求对数据库中所有记录R按长度从小到大的顺序进行排列;并且按照某种特定顺序对记录中元素进行排序来加快候选集检测的速度.
该算法采用谷歌稠密哈希(Google Dense Hash)来存储生成的候选集.整个算法可分为3个阶段:生成候选集阶段、验证阶段及索引阶段.生成候选集阶段约需F次hash插入或更新操作,F为通过长度过滤的记录中的全部元素数量;验证阶段需对记录和每一个候选集的T-1个后缀进行扫描,约次元素访问操作,C为整个算法的总候选集数量为记录的平均长度;索引阶段需I次索引插入操作,I为 F中被索引的元素数,且存在I=F-n(T-1),n为通过长度过滤的记录数量.
算法的候选集大小是影响All-pair算法性能最重要的参数,但其很难精确估量.最坏情况下,n条记录的数据集可能考虑的候选集数量为C=n(n-1)/2.
与普通反向索引中反向列表为ID的有序序列不同,All-pair的反向列表结点由ID以及指向该记录未索引部分数据的指针组成.该算法需在内存保留被索引的记录,因此反向列表的空间需求为2I+F个整型空间(文中假设元素、ID和指针各需一个整型内存空间),另外该算法最大需有存储n-1个候选集的hash空间(All-pair的反向索引目录部分采用直接索引,需大于最大元素大小的索引大小).
2.2 PPJoin算法
All-pair算法的缺点在于可能生成过于庞大的候选集,从而导致算法性能降低.PPJoin算法[3]在All-pair算法的长度过滤基础上引入前缀过滤和位置过滤来改进All-pair算法的性能.
前缀过滤要求按照频率升序对所有记录进行排序.因前缀中的元素在数据库中出现的频率相对较低,因此,探测到的候选集会大大减少.
位置过滤要求在元素E的反向列表中同时索引记录x和E 在x中的位置pos,即〈x,pos〉对.位置pos同样有助于快速过滤不符合条件的候选集,从而降低候选集大小.对T-覆盖而言,因其是固定阈值T的,故所有大于T的记录均有相同的T-1个未索引的后缀,这也使得任一候选记录y'和当前记录x潜在的覆盖值总是大于等于T,PPJoin的位置过滤不会起作用,故文中的PPJoin并未应用位置过滤.
PPJoin算法生成候选集阶段需I次hash操作;验证阶段约需要次元素访问操作为当前元素和候选集通过索引已检测到的覆盖值;索引阶段同样需要I次索引插入操作.
PPJoin算法的反向列表结点由ID、指向记录的指针,以及记录的大小组成.因此,其反向列表部分空间需求为3I+F,另外同样需要和All-pair相同的存储候选集的空间.
文献[3]进一步提出了通过海明距离对候选集后缀进行有效过滤的PPJoin+算法.
3 DTI索引结构及基于DTI的相似度连接算法
与All-pair和PPJoin算法类似,文中提出的算法同样基于流的思想,对每一个到来的记录x,通过索引探测符合相似度阈值T的所有的记录y,这样对相同的相似对〈x,y〉和〈y,x〉只需统计一次.与上述两个算法不同之处在于:(1)文中提出的DTI索引是基于trie的动态索引结构,而非基于反向索引结构;(2)DTI基于y的所有元素(而非部分元素)构建索引;(3)通过基于DTI结构的算法可以直接得到T-覆盖查询的结果,而无需生成任何候选集,从而可以提高算法执行的效率.
3.1 DTI结构
DTI结构的基本思想是:将数据库中的每条记录映射为一条从根到叶的trie路径.记录中的每一个元素映射到trie中的一个结点,多条记录的公共前缀映射为trie中的一条公共的路径.
DTI结构由目录和trie两部分组成.DTI的目录和反向索引的目录相似,由有限全局U中的元素构成.每一个目录项包含U中一个独立的元素以及指向该元素对应的第一个trie结点的指针.表1给出了一个包含5条记录的简单值升序数据库,以表1的前4条记录创建的DTI结构如图1所示,其中root为一个空的根结点.

表1 一个简单的值升序数据库Table 1 A simple database with value-ascending order

图1 根据表1前4条记录创建的DTI结构Fig.1 DTI created for the first 4 records of Table 1
DTI的trie部分主要由trie结点组成,trie结点的结构如图2所示.

图2 trie结点结构Fig.2 Structure of trie node
图2中的各字段描述如下:
Elem,代表元素E本身;trie结点N代表的元素E称之为N的源,结点N则称为元素E的一个出现;若R为任意包含E的记录,称R映射的trie路径上的E的出现为E关于R则的出现;元素E在trie中可有多个出现,但E关于记录R的出现最多只有一个.
NodeLink,链接到E的下一个出现的指针;E的所有出现的集合称之为E的出现集,出现集可以方便地通过目录中该元素的指向trie结点的指针和NodeLink获取.
Children,指向当前结点子结点集的指针.
Parent,指向当前结点父结点的指针.
NodeInvertedList,又称结点反向列表(简称NIL),是所有映射路径中包含从根到当前结点的前缀路径的记录的ID的集合;文中规定,根结点的NIL为所有记录的ID的全集;各个结点的NIL见图1中结点左侧的集合.
Depth,用于在查询过程中设置查询深度,见下节.
图1中,元素a的唯一出现即结点1(结点右侧数字表示结点号),其结点前缀路径为root a,而映射路径包含这个结点前缀路径的记录分别是记录0、2(ID 为0、2 的记录).因此,结点1 的 NIL 为{0,2}.结点的NIL可以在DTI的创建过程中生成.
创建DTI结构的算法非常容易,具体算法文中不再赘述.
定理2 DTI中,任一非根结点的NIL是其父结点的NIL的子集.
证明 从结点前缀路径的包含关系易见.
3.2 Dtrie-allpair:基于DTI的相似度连接算法
为了有效描述Dtrie-allpair算法,文中引入查询结点和查询深度的概念.
定义2 查询结点:所有源包含于当前记录x中的结点.
定义3 查询深度:查询结点的查询深度定义为从根到该查询结点的路径(含该结点)中查询结点的数量.查询结点N的查询深度用DN表示.根结点非查询结点,为了便于处理,文中规定根结点的查询深度为0.查询深度为D的查询结点称之为D-结点.
给定图3所示DTI结构和新到的当前记录x={b,e,g},可见,结点5为查询结点,其查询深度为3,因为从root到结点5的路径中,有结点2、3和53个查询结点.目录中深色背景为当前记录元素,trie中深色背景结点为查询结点.

图3 在DTI上执行查询Fig.3 Executing query on DTI
定理3 对当前记录x而言,所有T-结点的NIL的并集为满足x的T-覆盖查询的结果.
证明 首先证明正确性,也即是证明所有T-结点的NIL的并集满足命题.
设N'为任意T-结点,则从该结点到根的路径上有T个查询结点,故该结点的NIL对应的所有记录均包含这T个结点的源.另外根据定义2,这T个查询结点的源均出现在x中,故正确性成立.
其次证明完备性,即证明T-结点的NIL的并集包含了相似度查询的全部结果.
N'为任意T-结点,Nd为N'的任一子孙结点,Na为N'的祖先结点.首先,由定理2可知,Nd的NIL是N'的NIL的子集,Nd的NIL已包含在T-结点的NIL中;其次,由定理2可知,Na的NIL为N'的NIL的超集,可分为终结于T层或T层查询结点之后的ID与终结于T层查询结点之前的ID两部分,第1部分ID显然包含在T层结点的NIL中,对于第2部分ID,其从根到叶结点的路径上查询结点数量小于T,故该部分不可能符合要求.
综上可见,所有符合条件的结果均包含在T-结点的NIL的并集中,故定理得证.
如图3所示DTI结构和当前记录x={b,e,g},T=2,则2-结点为结点3和10,其 NIL的并集为{0,3},故ID为0和3的两个记录和x的覆盖大于等于2.
基于上述定义和定理,文中的问题就转换到如何快速有效地查找T-结点上来.
对每一个查询结点N,可通过式(1)计算其查询深度:

式中,N.Pred表示结点N的前驱查询结点,即从该查询结点到根的路径中距离N最近的查询结点.为此,提出了查找任意查询结点的前驱查询结点的算法(FindPredecessor算法),如下所示:
FindPredecessor算法中,递归判断查询结点N的父结点是否是查询结点.在判断某结点是否是查询结点时,基于以下定理,只需要判断该结点的源是否存在于x的前面一部分元素中:
定理4 对特定的元素序而言,若E为x中一个元素,N为E的任一出现,Na为N的任一祖先结点,则Na的源如在x中,其位置必在E之前.
证明 由x中元素序靠前的元素映射的结点为元素序靠后的元素映射结点的祖先结点易见定理成立.
根据定理4,若E在x的位置为pos,要判断Na是否是查询结点,则只需查找其源是否存在于x的前pos-1个元素中即可.故而在FindPredecessor算法中,引入参数查询集下标参数k,用来减少比较次数.
图3中,结点5的源为g,为记录{b,e,g}的第3个元素.若要判断其父结点——结点4是否是查询结点,无需判断结点4的源——元素f是否存在于整个查询集中,只需判断f是否存在于前两个元素{b,e}中即可.
在实现FindPredecessor算法的基础上实现Get-OverLapPair算法,如下所示:


GetOverLapPair算法执行如下:对x中的第一个元素的所有出现,因其之前没有其它查询结点,故可以安全地将其查询深度置为1;然后依次对x中其它元素的每一个出现调用FindPredecessor算法查找其前驱查询结点,并按照式(1)计算其查询深度;计算的查询深度直接存储于该结点的Depth域中.如果某个查询结点的查询深度等于T,则将该结点的NIL中每一个ID与x.ID组成的结果对加入到结果集中.
完整的Dtrie-allpair算法如下所示.在算法中,应用了长度过滤,如果,则不对x进行任何处理.

3.3 算法分析
由Dtrie-allpair算法可见,该算法只需遍历数据库一次,对每一条记录x先查询后索引.由于应用长度过滤,因此覆盖阈值越高,过滤后需要处理的记录就越少.

trie结点为DTI结构的主要空间开销.若M为DTI中的trie结点数量,每个结点除NIL域外的其余部分,需5个整型空间.易见,所有结点的NIL中ID的数量等于索引的元素数量F,故trie结点共需空间为5M+F.
3.4 进一步优化
第3.1节中根据值升序来创建DTI结构.本节进一步通过开发其它序来提升Dtrie-allpair算法的性能.
频率降序按元素在整个数据库中的频率从高到低的顺序安排元素在各记录中位置,这使得根据频率降序创建的DTI结构具有最少的结点,从而降低了自连接所需访问的节点数,提升了算法的性能.表1数据库对应的频率降序数据库如表2所示.

表2 表1对应的频率降序数据库Table 2 Frequncy-descending order database of Table 1
根据表2的前4条记录创建的DTI结构如图4所示.可见采用频率序创建的DTI仅包含10个结点,而图1的DTI包含11个结点.
长度升序按元素数量从低到高的顺序安排记录在数据库中的位置,这同样有助于提升算法的性能.通过长度升序,并不会降低索引全部记录最终创建的DTI结点数,但由于较短的记录优先被索引,故在自连接过程中倾向于访问更少的结点.表1数据库对应的长度升序数据库如表3所示.根据表3前4条记录创建的DTI结构如图5所示.
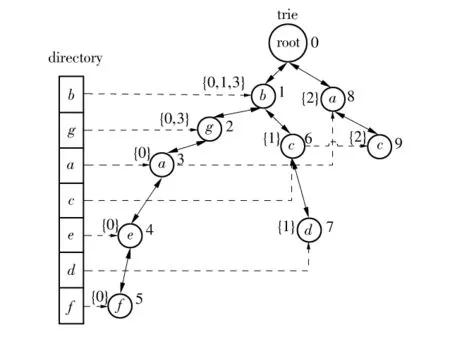
图4 根据表2前4条记录创建的DTI结构Fig.4 DTI created for the first 4 records of Table 2

表3 表1对应的长度升序数据库Table 3 Length-ascending order database of Table 1
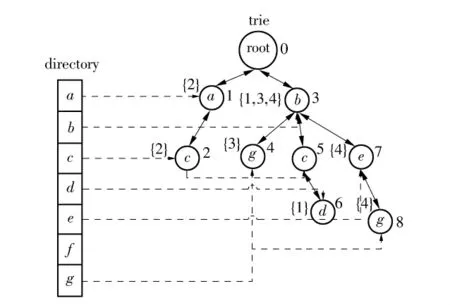
图5 根据表3前4条记录创建的DTI结构Fig.5 DTI created for the first 4 records of Table 3
对表1中的5条记录,在DTI中查询时需要访问的结点数依次为 0、1、2、3、5,共需 11 次结点访问;而表3中长度降序的5条记录需访问的结点数依次为 0、0、2、2、5,只需9 次结点访问.
通过组合频率降序和长度升序,可同时降低创建的结点和访问的结点,进一步提升Dtrie-allpair算法的性能.因篇幅限制,具体分析文中不再赘述.
4 实验
4.1 实验环境
为了评估 Dtrie-allpair算法的性能,将 Dtrie-allpair算法和All-pair算法及PPJoin算法进行对比.实验主要硬件平台:CPU Intel Core i5-2410M@2.30GHz,内存 4 GB;软件环境:Windows732 位,Microsoft Visual Studio C++2008.
采用两个不同的数据集验证文中的算法.第一个数据集为 UCI KDD Archive 的 msweb[16]数据集,包含用户对www.microsoft.com站点虚拟区域一周的访问日志.每个集合表示一次用户会话时访问的区域的集合,共有32711条记录,词汇表中包含294个独立元素,记录最大势为35.
第二个数据集同样采用UCI KDD Archive的msnbc数据集,共有989818条记录,该数据集词汇表较小,仅包含17个独立元素,最大记录长度为17,平均记录长度为5.7.
4.2 算法比较
对3种算法,均采用长度过滤,对 All-pair和PPJoin算法,只索引其前缀.
3种算法均要求对数据进行相应的预处理.Allpair算法要求数据集按记录长度升序有序,记录内的元素同样升序排序,以加快候选集的校验;PPJoin除需All-pair的要求外,还需对数据集按频率升序排序;Dtrie-allpair在组合频率降序和长度升序时相对PPJoin并不会带来更多的预处理代价.预处理的时间开销所占比例非常小,且通常可以离线进行,因篇幅限制,文中不对预处理过程做更详尽的介绍.除特别声明外,以下对Dtrie-allpair算法采用的数据集均采用组合频率降序和长度升序进行预处理.
对3种算法,分别在相似度阈值 T为2、4、6、8、10时各执行一次自连接.msweb数据集下3种算法的执行时间如图6所示.

图6 msweb数据集下3种算法的自连接执行时间Fig.6 Self-join time of three algorithms under msweb data
由图6可见,Dtrie-allpair算法的执行效率高于All-pair、PPJoin两种算法,并且在阈值较小时具有更大的优势.T=2时,Dtrie-allpair算法执行自连接仅需0.5s,而 All-pair算法、PPJoin算法分别需要90s、54 s,Dtrie-allpair算法的效率提高近两个数量级;T=10时,Dtrie-allpair算法约需0.09 s时间完成自连接,而All-pair算法和PPJoin算法分别需要0.5 s和0.3s来完成.
对msnbc数据集,实验中观察到类似的结果,对T=2的情况,All-pair算法和PPJoin算法均不能在1h内结束.msnbc数据集下3种算法的执行时间如图7所示.

图7 msnbc数据集下3种算法的自连接执行时间Fig.7 Self-join time of three algorithms under msnbc data
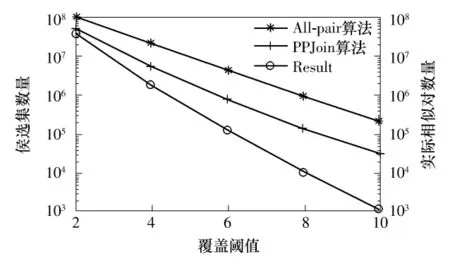
图8 msweb数据集下不同算法产生的候选集及实际相似对数量Fig.8 Generated candidates and number of real similar pairs of different algorithms under the msweb data
All-pair算法和PPJoin算法效率较低的一个重要原因在于,这两个算法需要生成大量的候选集,然后对候选集逐一验证.覆盖阈值越小,需要验证的候选集和最终的结果集就越大,因此,需要的执行时间也就越长.而Dtrie-allpair算法不产生任何候选集,通过索引可以得到直接的结果,因此效率大大提高.msweb数据集下All-pair算法、PPJoin算法需要验证的候选集数量以及实际相似对的数量如图8所示.图例中Result代表最终结果对,对Result而言,纵坐标代表最终结果对数量;对All-pair算法和PPJoin算法而言,纵坐标代表候选集数量.
4.3 序对Dtrie-allpair算法的影响
为了考察不同的序及其组合对Dtrie-allpair算法的影响,文中对数据集分别按值升序、频率降序、值升序加长度升序以及频率降序加长度升序进行相应的预处理.在msweb数据集下,对不同预处理的数据集执行Dtrie-allpair算法得到的自连接时间和访问的节点数分别如图9和10所示.从图中可见,频率降序和长度升序组合在自连接过程中访问最少的节点数,在T=2时,其访问节点数仅为只用值升序的1/4,从而需要的执行时间也大大降低.

图9 msweb数据集下4种序的自连接时间Fig.9 Self join time of four kinds of orders under the msweb data
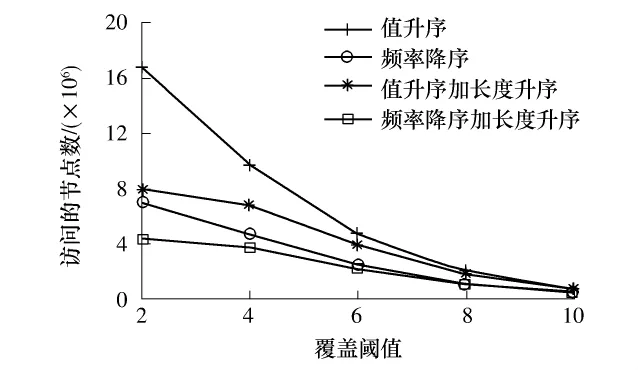
图10 msweb数据集下4种序访问的节点数Fig.10 Nodes accessed of four kinds of orders under the msweb data
5 结语
传统的T-覆盖算法通常是基于生成-测试的框架来执行,它们需要在测试阶段对成阶段生成的候选集逐一验证,当候选集非常大时,系统的性能不可避免地会降低.针对传统算法这一不足,文中提出了一种DTI结构,并基于该结构构建了Dtrie-allpair算法,通过该算法可以直接得到allpair连接的结果,而不产生任何候选集,有效克服了传统算法需生成并验证候选集带来的开销.通过实验对Dtrie-allpair算法与All-pair算法、PPJoin算法进行对比,结果表明Dtrie-allpair算法具有明显的优势;通过频率降序和长度升序组合可有效降低DTI中访问的结点数,从而提升Dtrie-allpair算法的性能.Dtrie-allpair算法也存在一定的缺点,主要在于DTI结构倾向于需要更高的空间开销,这是下一步研究中需要解决的问题.
[1] Chaudhuri S,Ganti V,Kaushik R.A primitive operator for similarity joins in data cleaning[C]∥Proceedings of the 22nd International Conference on Data Engineering.Atlanta:IEEE Computer Society,2006:5-16.
[2] Arasu A,Ganti V,Kaushik R.Efficient exact set-similarity joins[C]∥Proceedings of the 32nd International Conference on Very Large Data Bases.Seoul:ACM Press,2006:918-929.
[3] Xiao C,Wang W,Lin X,et al.Efficient similarity joins for near duplicate detection[C]∥Proceedings of the 17th International Conference on World Wide Web.Beijing:ACM Press,2008:131-140.
[4] Hoad T,Zobel J.Methods for identifying versioned and plagiarized documents[J].Journal of the American Society for Information Science and Technology,2003,54(3):203-215.
[5] Li C,Lu J,Lu Y.Efficient merging and filtering algorithms for approximate string searches[C]∥Proceedings of the 24nd International Conference on Data Engineering.Cancún:IEEE Computer Society,2008:257-266.
[6] Helmer S,Moerkotte G.A performance study of four index structures for set-valued attributes of low cardinality[J].The International Journal on Very Large Data Bases,2003,12(3):244-261.
[7] Helmer S,Aly R,Neumann T,et al.Indexing set-valued attributes with a multi-level extendible hashing scheme[C]∥Proceedings of the 18th International Conference of Database and Expert Systems Applications.Regensburg:Springer-Verlag,2007:98-108.
[8] Mamoulis N.Efficient Processing of joins on set-valued attributes[C]∥Proceedings of the 2003 ACM SIGMOD International Conference on Management of Data.San Diego:ACM Press,2003:157-168.
[9] Terrovitis M,Passas S,Vassiliadis P,et al.A combination of trie-trees and inverted files for the indexing of set-valued attributes[C]∥Proceedings of the 15th ACM International Conference on Information and Knowledge Management.Arlington:ACM Press,2006:728-737.
[10] Hossain S,Jamil H M.A hybrid index structure for setvalued attributes using itemset tree and inverted list[C]∥Proceedings of the 21st international Conference on Database and Expert Systems Applications.Bilbao:Springer-Verlag,2010:349-357.
[11] Agrawal P,Arasu A,Kaushik R.On indexing error-tolerant set containment[C]∥Proceedings of the 2010 International Conference on Management of Data.Indianapolis:ACM Press,2010:927-938.
[12] Xiao C,Wang W,Lin,X,et al.Top-k set similarity joins[C]∥Proceedings of the 25nd International Conference on Data Engineering.Shanghai:IEEE Computer Society,2009:916-927.
[13] Sarawagi S,kirpal A.Efficient set joins on similarity predicates[C]∥Prceedings of the 2004 ACM SIGMOD Intevnational Conference on Management of Data.Paris:ACM Pvess,2004:743-745.
[14] Bayardo R,Ma Y,Srikant R.Scaling up all pairs similarity search[C]∥Proceedings of the 16th International Conference on World Wide Web.Banff:ACM Press,2007:131-140.
[15] Wang J,Li G,Feng J,et al.Trie-join:efficient triebased string similarity joins with edit distance constraints[J].Proceedings of the VLDB Endowment,2010,3(1/2):1219-1230.
[16] Bay S D,Kibler D,Pazzani M J,et al.The uci kdd archive of large data sets for data mining research and experimentation[J].ACM SIGKDD Explorations Newsletter,2000,2(2):8185.

