活用转换法巧解物理题

杨志宇 孙丽娜

(望奎县第一中学 黑龙江 绥化 152100)

转换法，就是把要解决的复杂难解的物理问题转换成一个与之相关的简单、容易的物理问题，从而顺利解决，达到化难为易，化繁为简的效果.

1 对象转换

在处理物理问题时，一般只关注与问题相关的物体或者系统.但由于各种原因，关注的物理对象所处的情境过于复杂，从而使所研究的问题进入“死胡同”.如能灵活地转换研究对象，往往可使研究的问题得到顺利解决.

【例1】如图1所示，条形磁铁放在桌面上.一条通电的直导线由S极的上端平移到N极的上端过程中，导线保持与磁铁垂直.导线的通电方向如图1.则这个过程中磁铁受到的摩擦力(磁铁保持静止)

A．为零

B．方向由向左变为向右

C．方向保持不变

D．方向由向右变为向左

解析：由于本题研究的是磁铁的受力情况，很多学生选择了以磁铁为研究对象，然而磁铁电流间作用力并没有固定的公式及规律，从而导致问题无法解决.这时如能把研究对象转换成通电导线，再根据牛顿第三定律，得出磁铁的受力情况，问题很容易得以解决.正确选项为选项B.

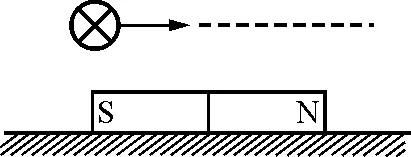
图1

2 过程转换

我们习惯于正向思考物理过程，往往忽略了对物理过程的逆向思考.

【例2】如图2所示，一充电的平行板电容器，板长为L，两板间距为d.现将一带电微粒(重力不计)从下极板的左边缘射入电场中，结果带电微粒刚好从上极板的右边缘水平射出.试确定带电微粒射入电场时，速度方向与下板的夹角θ应是多少.

图2 图3

解析：若将微粒从上极板右边缘以v0cosθ沿水平射入，带电微粒在电场中做的是类平抛运动，如图3所示.此时的运动与原题的运动显然是可逆的;这样就将原运动转换成新的运动.

由题意可知L=v0tcosθ

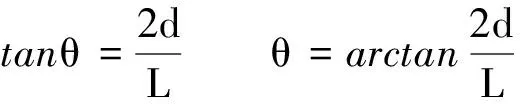
3 图形转换

在解决某些物理问题时，要多考虑能否把抽象的物理问题转换成直观的图像；这样的好处不但可以帮助分析题意，甚至可以直接得出结论.

【例3】如图4所示，轻弹簧一端与竖直墙壁连接，另一端与一质量为m的木块连接，放在光滑水平面上，弹簧的劲度系数为κ，处于自然状态.用水平力向右缓慢拉物体，使物体前进x.求这一过程中拉力对物体做了多少功.

解析:缓慢拉动物体，可认为物体处于平衡态，故拉力等于弹力大小，即F=κx.画出F与x的关系图像，如图5所示.F与x所围成的面积的意义表示F所做的功.易得

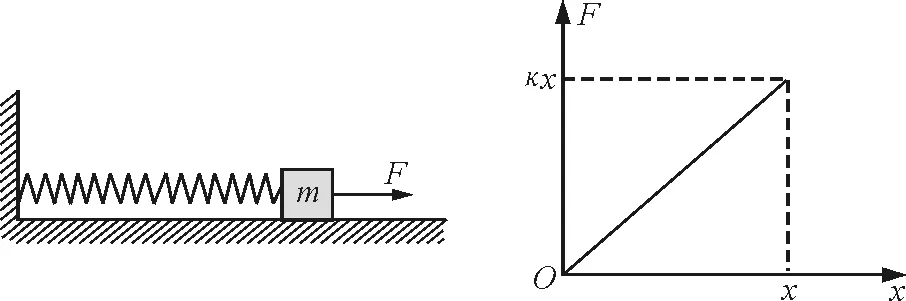
图4 图5

4 等效转换

等效转换就是将一个物理问题、物理量、物理方法，转换成等效果的物理问题、物理量、物理方法，以到达快速处理问题的目的.

【例4】如图6所示，设有两面均垂直于地面的竖直光滑墙A和B，两墙水平距离为1．0 m.从距地面高19．6 m处的一点C以初速度5．0 m/s沿水平方向抛出一个小球.设球与墙的碰撞为完全弹性碰撞.求小球落地点距墙A的水平距离和落地前与墙壁碰撞的次数.(忽略空气阻力，取g=9．8 m/s2)

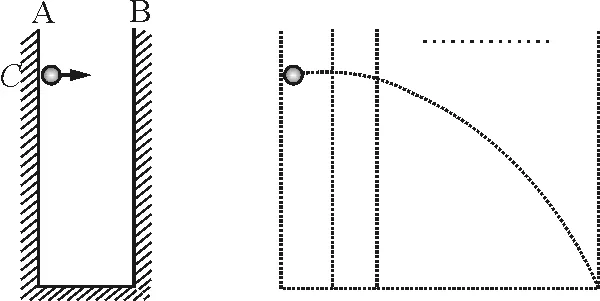
图6 图7

解析：设小球与墙壁碰撞前的速度为v，因为是弹性碰撞，所以在水平方向上以原速率弹回，即v′=v.又因为墙壁光滑，所以在竖直方向上速率不变，从而小球与墙壁碰撞前、后的速度v和v′关于墙壁对称，以后的碰撞亦然.因此，可将小球的运动等效为连贯的平抛运动来处理，如图7所示.由

可得碰撞次数为n=10次.由于n刚好为整数，故小球最后落在A墙脚，即落地点距离A的水平距离为零.

5 模型转换

在解决物理问题时，如能把研究的物理问题转换成熟悉的物理模型，不但可以迅速解题，也能培养学生的发散思维，是一种很好的方法.

【例5】一汽车在轨道MN上行驶速度v1可达到50 km/h.在轨道外的平地上行驶速度v2可达40 km/h.与轨道的垂直距离为30 km的B处有一基地,如图8.问小车从基地B出发到离D点100 km 的A处的过程中,最短需要多长时间?

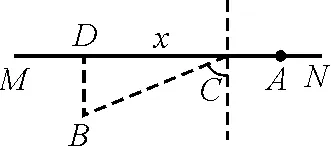
图8

解析：小车从B处到A处的运动可类比为光的全反射现象的临界状态.故有

由图可知

小车运动时间

代入数据得

x=40 kmt=2.45 h

6 角度转换

很多物理问题涉及到三维(立体)角度.为了研究问题方便或者简化问题难度需要将三维角度转换成二维(平面)角度，以求简单快捷的处理问题.

【例6】如图9所示，水平放置的光滑的金属导轨M,N，平行地置于匀强磁场中，间距为d.磁场的磁感应强度大小为B，方向与导轨平面夹为α.金属棒ab的质量为m，放在导轨上且与导轨垂直.电源电动势为E，定值电阻为R，其余部分电阻不计.则当开关闭合的瞬间，金属棒ab的加速度为多大？

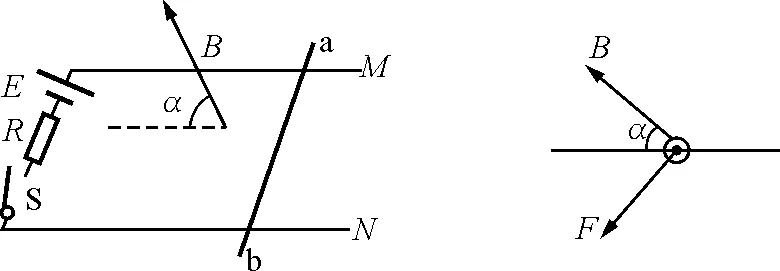
图9 图10

解析：由于B，I，F三者垂直的关系，使得问题处于三维角度.这时就需要把三维的物理问题转换成二维问题,如图10所示.易得

整理得