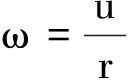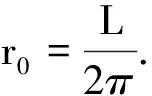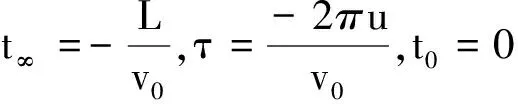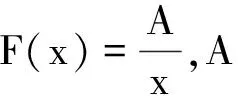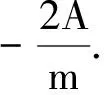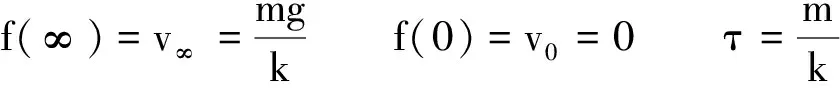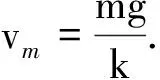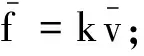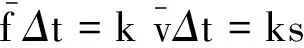利用结论巧解“甲虫和橡胶带”问题

郑金

(凌源市职教中心 辽宁 朝阳 122500)

贵刊的《均匀拉伸的橡胶带上任意一点的速度公式》[1]一文，通过高等数学的微积分知识推导出了在任意时刻t橡胶带上各位置x处的对地速度，但没有求出总时间.本文将给出一个数学结论，同时把橡胶带按直线拉伸的过程等效为按圆周扩大的过程，利用等效法和结论对原题作解答，可避免积分过程，且直观简便.

1 数学结论

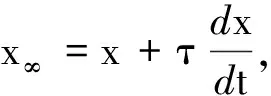
即

若变量x=f(t)是时间的函数，则式中的常系数τ称为时间常量，其国际单位是s.

2 结论证明

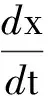
两边积分为

即

可知

则

代入初始条件t=0,x=x0，得C=x∞-x0，所以

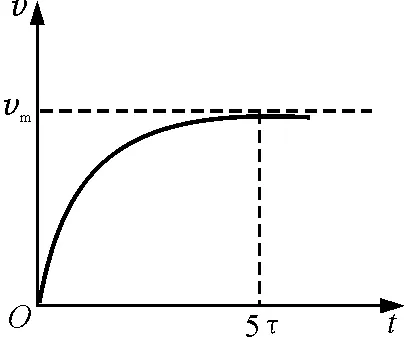
由此可见，变量x随时间t按指数规律变化，从理论上看，需要经历无限长的时间才能达到稳态f(t∞)=f(∞).但实际上，因为e-5≈0.006 7≈0，所以可认为当t=5τ时，变量已趋近于稳态值f(∞).这一变化过程称为瞬态过程.从物理上说，上述结论可称为瞬态过程的结论.从数学上说就是关于一阶常系数线性微分方程的结论.

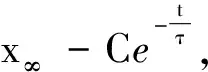
常见的瞬态过程是某一变量随时间呈指数规律变化.而另类瞬态过程则是某一变量随另一个非时间变量呈指数规律变化.

3 结论应用

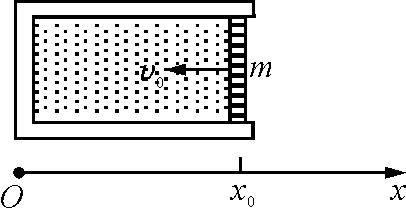
【原题】[1]一条水平的橡胶带长为L，一端固定在墙上，另一端是自由端．令自由端以速度v0运动而将橡胶带不断地均匀拉长．同时，橡胶带上的一只甲虫从墙开始沿橡胶带向自由端运动，甲虫在橡胶带上的速度始终为u，且u

图1

解析[2]：设想橡胶带围成一个圆周，圆心为O点，橡胶带的起点和终点重合为一点A，如图1．由于橡胶带是均匀伸长的，则圆周随时间均匀增大，但橡胶带上任意一个定点始终在同一半径上，即在圆周均匀增大的过程中，橡胶带上任一点的运动为沿同一半径的直线运动.

x=L+v0t

则圆周半径为

因此角速度为

在时刻t的角位移为

变形为一阶常系数线性微分方程的标准形式为

由此可知，时间变量t将随角度变量θ按指数规律变化，是另类瞬态过程.利用结论得

到终点时，θ=2π，所以经历的时间为

瞬态过程的结论可用来解答很多大学物理问题，现举两例.

解析:(1)由理想气体状态方程有pV=nRT，气体对活塞的弹力为

图2

(2)由牛顿第二定律列微分方程为

其中速度

则

变形为

当活塞停止时，vx=0.所以此时活塞的位置坐标为

活塞初速度v0越大，停止时被压缩气体体积越小.当v0→∞时，压缩气体体积趋于零，即稳态值趋于x∞=0.但实际上是不可能的.

【例2】[4]质量为m的质点，在有阻力的空气中无初速度地自离地面高为h的地方下落.如阻力与速度成正比，试研究其运动.

解析：设质点下落速度v=f(t)，所受空气阻力f=kv，同时受重力G=mg，以竖直向下为正方向，由牛顿第二定律有

由此得关于v的一阶常系数线性微分方程的标准形式为

由瞬态过程的结论可知速度随时间变化的关系式为

所以速度变化规律为

表明与速度共线的正比例线性力的冲量跟位移成正比.

图3

对质点下落过程，由动量定理有

mgt-ks=mvt-mv0

由此得质点下落的位移为

如果把空气阻力表示为f=mkv，则质点运动规律为

如果以质点的落地点为坐标原点O，竖直向上为x轴建立坐标系，则质点的运动规律为

综上可见，求运动速度和位移避免了积分运算，比原解简便很多.因此利用结论解题，可化繁为简、提高效率；还可对由积分过程所得结果进行检验，一举多得．

参考文献

1 项林川.均匀拉伸的橡胶带上任意一点的速度公式.物理通报，2010(8):72

2 赵灿冬.用角速度巧析“蚂蚁爬橡皮绳悖论”. 物理教师，2005,26(8)：45

3 漆安慎，杜婵英.力学基础.北京：高等教育出版社，1982.144～145

4 周衍柏.理论力学教程(第二版).北京：高等教育出版社，1986. 39～40