水下基盘井口平台桩基群桩效应数值模拟

,

(胜利油田胜利勘察设计研究院有限公司，山东 东营 257026)

水下基盘井口平台将隔水管通过水下基盘打入海底，井口隔水管兼做平台的基础。由于隔水管的间距很小，在进行桩基计算时按照规范的规定需考虑群桩效应对桩基承载力的影响[1]，但相关规范没有明确说明该如何考虑。鉴于此，以胜利埕岛油田CB12D水下基盘井口平台为例，用通用有限元软件ANSYS建立群桩的整体分析模型，将群桩和群桩周围土体看作一整体，探讨群桩效应对桩基承载力的影响。

1 隔水管及土壤基本参数

隔水管力学性能参数及几何尺寸见表1。

表1 隔水管力学性能参数及几何尺寸

隔水管的平面布置见图1，其中横向桩距1.6 m，纵向桩距为1.8 m；除中间一根桩的桩径为1.2 m外，其余桩的桩径均为0.9 m。

本次研究桩周土的性能参数见表2。

2 有限元模型的建立

2.1 DP材料介绍

土壤和岩石属于颗粒状材料，此类材料受压屈服强度远大于受拉屈服强度，且材料受剪时，颗粒会膨胀，常用的Von Mises屈服准则不适合这种材料。在土力学中常用的屈服准则为Mahr-Conlomb准则，另一个更准确描述这种材料的强度准则为Drucker-Prager屈服准则[2]，使用Drucker-Prager屈服准则的材料简称为DP材料。在岩石、土壤的有限元分析中，采用DP材料可得到较为精确的结果。

图1 桩的平面布置

Drucker-Prager屈服准则是对Mahr-conlomb准则的近似，用以修正Von Mises屈服准则，即在Von Mises表达式中包含一个附加项。其屈服面并不随着材料的逐渐屈服而改变，没有强化准则，其屈服强度随着侧限压力的增加而相应增加，其塑性行为被假定为理想弹塑性，屈服面见图2。

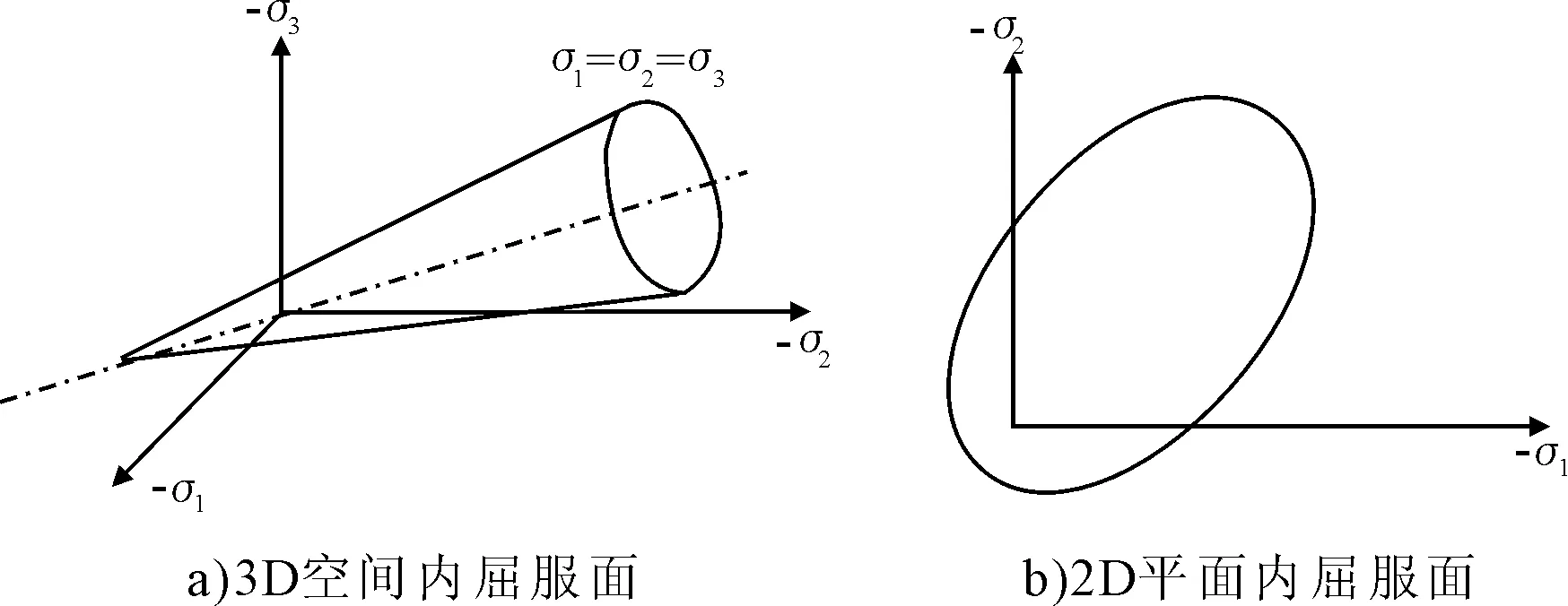
图2 DP材料屈服面

DP模型其屈服面的(等效应力表)表达式为

(1)

式中：σm——静水压力，σm=1/3(σx+σy+σz)；

S——偏应力；

β——材料常数；

M——Mises屈服准则中的M。

2.2 模型的建立

根据前述基本参数分别建立桩和桩周土的模型。在建模过程中为了最大限度地消除边界效应对计算结果的影响，同时又不致模型过大使得计算时间大幅增加，经过多次试算，最后确定计算单桩承载力时取桩周土的直径为桩径的5倍，计算群桩承载力时取桩周土的长宽为桩所在区域长宽的5倍，深度均取桩长的1.25倍。此时，在竖向荷载作用下，桩对桩周土外边缘的影响很小，可以忽略。由于在竖直荷载作用下，单桩模型关于XZ及YZ平面对称，故可以只建1/4模型并施加对称约束条件来实现整个模型的计算结果。群桩模型和边界条件均关于XZ平面对称，故可以只建1/2模型并施加对称约束条件来实现整个模型的计算结果。

利用ANSYS单元库中的壳单元SHELL63建立桩体模型[3]，实体单元SOLID45建立土体模型，定义土体为DP材料，按表1所列的土壤资料将土体分为11层，并定义每层土的属性。所建单桩、群桩模型网格划分见图3。为了使计算能很好地收敛，在网格划分时将桩体的网格划分得相对较密，土体的网格相对较疏。

利用ANSYS单元库中的目标单元TARG170和接触单元CONTA173，分别将桩侧和桩周土、桩端和桩端土接触的面定义为一对接触对，以此来模拟桩土之间的相互作用，其中将桩侧和桩端的外表面定义为目标面，土体上的面定义为接触面。

图3 网格划分

2.3 边界条件的施加

分析时，对模型的对称面施加对称约束，并约束土体外表面上节点的6个自由度，在桩顶施加竖向作用力进行计算，有限元模型中，单桩及群桩边界条件的施加见图4。

图4 边界条件施加

3 桩基极限承载力的确定标准

桩基极限承载力可以依据计算得到的荷载-位移曲线确定。对于计算所得的荷载-位移曲线，可分为两种典型情况，即陡变型曲线和缓变形曲线。在陡变型曲线中，存在明显的第二拐点，可将该拐点对应的荷载作为地基的极限承载力；而在缓变形的曲线中，没有明显的第二拐点，对于该种曲线，需要通过多种分析方法判定其极限承载力，规范中规定了两类，即承载力极限状态和正常使用极限状态。因此桩基的极限承载力的确定也有两类。对于井口平台而言，通常上部结构对基础的沉降变形有较为严格的要求，因此桩基极限承载力按正常使用极限状态确定[4-5]。本文将桩端竖向位移量达到0.2 m时对应的竖向荷载确定为桩基的竖向极限承载力。

4 竖向荷载作用下桩的极限承载力

4.1 单桩极限承载力的确定

在单桩分析模型的桩顶施加竖向荷载,计算得出0.9 m和1.2 m桩径单桩的桩顶位移荷载曲线见图5和图6。由图5、6得出两种桩径的单桩竖向极限承载力分别为5 400和7 200 kN。在桩基达到极限承载力时，桩及桩周土体的有效应力云图见图7。

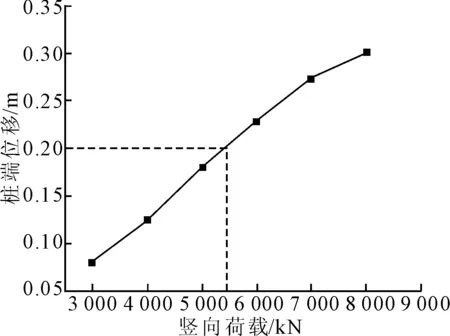
图5 0.9 m桩径单桩桩端位移荷载曲线

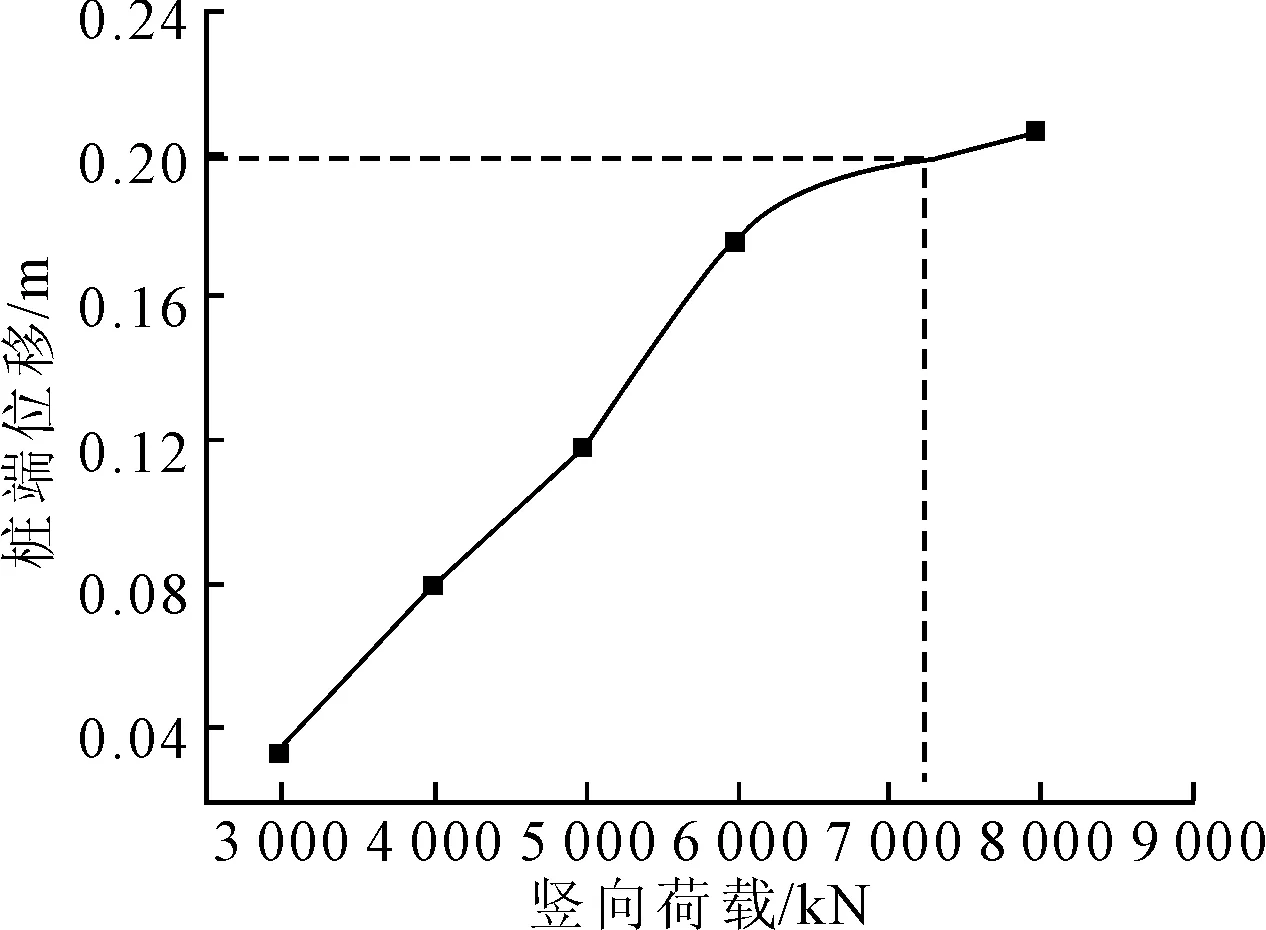
图6 1.2 m桩径单桩桩端位移荷载曲线

4.2 群桩极限承载力的确定

用ANSYS建立群桩的分析模型，在群桩桩顶施加竖向荷载，计算得出群桩桩顶的位移荷载曲线见图8。由图8得出群桩的竖向极限承载力为5 533 t。在群桩达到极限承载力时，桩及桩周土体的有效应力云图和竖向位移云图见图9～11。可以看出土体的最大有效应力和竖向最大位移均发生在桩顶泥面处的位置，并随着荷载的不断增大向四周和泥面以下不断延伸；由于桩体弹性变形的影响，使得桩体的最大竖向位移发生在桩顶的位置，在群桩基础达到竖向极限承载力时，桩的有效应力远小于桩体本身的屈服强度，由此也可以看出群桩基础的破坏是桩周土体的破坏。

图7 单桩Mises应力云图

图8 群桩桩端位移荷载曲线

图9 土体Mises应力云图

图10 土体泥面处位移云图

图11 桩体Mises应力云图

5 群桩效应系数的计算

为了描述群桩效应对群桩极限承载力的影响，特定义群桩效应系数η为

(2)

式中：Qu1——考虑群桩效应时群桩的极限承载力；

Qu2——不考虑群桩效应时所有单桩的极限承载力之和。

由计算得到群桩的竖向极限承载力见表3。

表3 计算所得群桩竖向极限承载力

6 结论

1)就胜利埕岛油田CB12D水下基盘井口平台桩基而言，考虑群桩效应时群桩的竖向极限承载力小于单桩竖向极限承载力之和，群桩效应系数为0.83；竖向极限承载力较不考虑群桩效应时降低了17%，由此可以看出群桩效应对桩基的承载力影响较大，在设计时需考虑。

2)群桩效应系数的确定是一个很复杂的过程，同时受桩径、桩距、桩间土、桩端土以及承台等诸多因素的影响，不同的井口平台需建立不同的模型进行计算。

[1] API RP 2A-WSD，Recommended practice for planning,designing and constructing fixed offshore platform-working stress design[S],2000.

[2] 龚晓南.土塑性力学[M].杭州：浙江大学出版社，1990.

[3] 王 佳.ANSYS工程分析进阶实例[M].北京:中国水利水电出版社,2006.

[4] 郑大同.地基极限承载力计算[M].北京:中国建筑工业出版社，1979.

[5] 横山辛满.桩结构物的计算方法和计算实例[M].唐业清,吴庆荪,译.北京，中国铁道出版社，1984.