基于双线性对的代理重加密方案

王会歌，曹 浩，刘 斌，沈 峰

（安徽科技学院理学院，安徽 凤阳233100）

基于双线性对的代理重加密方案

王会歌，曹 浩，刘 斌，沈 峰

（安徽科技学院理学院，安徽 凤阳233100）

代理重加密的概念是由Mambo和Okamoto提出来的，其功能是将用一个用户公钥加密的密文转换成用另一个用户的公钥加密的密文，且加密是针对同一个明文而言的。但是这类方案都是基于传统的PKI公钥密码体制和身份密码体制的。本研究提出了一个新的无证书代理重加密方案，新方案优于先前的方案且能实现多次代理重加密性质，其算法比其它方案更简单，并且给出了详细的CCA安全性证明。

无证书；代理加密；重加密；代理重加密

1 Introduction

A proxy re－encryption scheme was first introduced by Mambo and Okamoto in 1997［1］．In this scheme，aproxy is allowed to transform ciphertexts computed under Alice’s public key into different ciphertexts that can be decrypted by using Bob’s secret key．But both the proxy and Bob cannot obtain the underlying plaintext without the proxy’s cooperating．Alice or a trusted third party generates the proxy re－encryption key which re－encrypts the previous level ciphertexts into others．Proxy re－encryption key consists of the delegator’s （or Alice’s）private key and the other values．Proxy re－encryption system have many attractive applications such as secure e－mail forwarding system，attribute－based delegations，travel key and access control in networked file storage．It was these applications which would encourage many cryptographers to research a variety of schemes［2－7］．But most of these schemes are based on traditional PKC or ID－based public key cryptosystem．However，there is few such proxy re－encryption based on certificateless public cryptosystem．

In literature［8］，Toshihiko Matsuo presented a scheme for the transformation from ciphertexts encrypted under a traditional PKI－based public key into the ciphertexts that can be decrypted by a secret key for Identity－based encryption and the other one for the transformation from ciphertexts encrypted in identity－based encryption （IBE）manner into the different ciphertexts that can be decrypted by the other secret key for IBE．

In this paper we present a scheme for the transformation from ciphertexts encrypted by a certificateless public key cryptosystem into the ciphertexts that can be decrypted by another certificateless public key cryptosystem．And the algorithm of our scheme is simpler than that of other proxy re－encryption schemes．

2 Properties of Our Scheme

Our scheme achieves all the advantages in literature［8］，such as follows：

a）optimal secret key size．

b）optimal ciphertext size．

c）not need an additional algorithm or process for decrypting re－encrypted ciphertexts while it is required in literature［7］．

d）Our scheme is semantic secure in the random oracle model．

e）Our scheme meets multi－use property．

f）And it is easy to see that our algorithm is simpler than that of other schemes．

3 Backgrounds

In the following，we briefly describe the groups，the basic structure of Certificateless Public Key Encryption （CLE）that will be used in our construction．Pairings

We briefly review some facts about bilinear pairings and groups used in the scheme in this paper．

Definition 1Let G and G1be two multiplicative cyclic group of prime order p，and g be a generator of G．We say that G has an admissible bilinear map e：G×G→G1if the following conditions hold．

1．Bilinearity：e（ga，gb）＝e（g，g）ab，for all a，b∈Z＊p．

2．The map e is non－degenerate：e（g，g）≠1G1．

3．There is an efficient algorithm to compute e（ga，gb）for all a，b and g．

The Weil and modified Tate pairings on elliptic curves can be used to build such bilinear maps［9］．

Assumption Bilinear Diffie－Hellman Assumption（BDH）［10］Let g be a parameter generator which with system parameter k as input generates two cyclic groups G and G1of prime order p，agenerator g∈Gand a bilinear map e，We define the advantage of an algorithm A in solving the problem（given＜g，ga，gb，gc＞，to compute e（g，g）abc）

by：

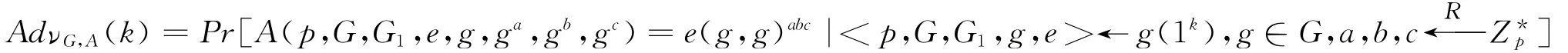
For any randomized polynomial time algorithm A （in k），the advantage AdνG，A（k）is negligible．

4 Construction of The scheme

We propose the construction of a proxy re－encryption scheme that is based on the certificateless public key cryptosystem．The scheme provides CCA security．It is very efficient in both computation and ciphertexts length and realizes multi－use．

We first assume that the proxy re－encrypts ciphertexts once．

SetUp （k）：Taking security parameter k as input and returns the system parameter parms，H is hash function as：H：｛0，1｝＊→and the master key is s and Ppub．

SecretValueG：Given the public parameters parms，user chooses a random value xIDi∈and sets xIDias secret value．

PublicKeyG：User runs the public key generation algorithm to generate the public key XIDi＝gxIDi，

PartialPrivateKeyG：KGC first picks a random r，computes R ＝grand computes QIDi＝ H（IDi，PKIDi）．Then takes as inputs parms，master key and a user’s identity ID as inputs．It returns a partial private key dID＝RsQID，and sends it to user IDithrough the security channel．

PrivateKeyG：Upon receiving the partial private key，user computes the private key skIDi＝ （dIDi）xIDi

Encryption：User first checks the efficiency of the public key through the equation e（XIDi，ppub）＝e（YIDi，g）．To encrypt a message m∈｛0，1｝＊under the identity IDi∈｛0，1｝＊，picks a randomu∈Z＊p，lets QIDi＝ H（IDi，PKIDi）and computes

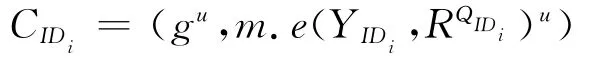
Decryption：Given the ciphertexts Ci＝ （C1，C2）and the secret key skIDiwith parms，then computes

Re－encryptionKeyG：Here we define user IDias the delegator and IDjas the delegatee．User IDjfirst runs above algorithm to generate his public key，partial private key，secret key and private key and send xIDito IDi．After that user IDicomputes the re－encryptionhen sends it to the proxy．

ReEnc：The proxy is given a ciphertexts CIDi＝ （C1，C2），the re－encryption key RKIDi－IDjand IDi，IDjwith parms，the proxy re－encrypts the ciphertexts CIDiinto CIDjas follows．

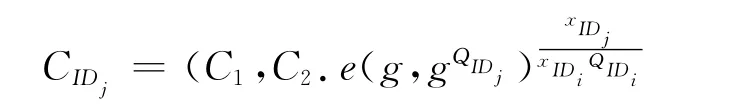
Dec：Given the re－encryption ciphertexts CIDj，computes plaintext as the description in the above decryption algorithm：

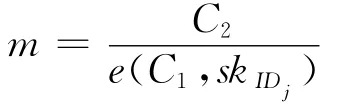
Multi－use：The proxy only needs to encrypt again the second part of the former ciphertexts by using the same re－encryption technique to realize the property of multi－use．Moreover，the length of the ciphertexts does not change．This is just the advantage that other schemes have not．So our new scheme can realize the multi－use and the length of the re－encryption ciphertext does not change compared to that of the former level ciphertexts and is shorter than that of other schemes．

5 Security Analysis

We prove that our proxy re－encryption scheme is IND－CCA secure against the following defined two types of adversaries．Assume the BDH problem is difficult．From the scheme we can see that as long as the cerficateless scheme is security，the certificateless proxy re－encrytption is security．

TheoremLet the hash function H is random oracle，if the BDH problem is difficult，our scheme is IND－CCA secure．Suppose A （A1，A2：A1is the type 1adversary and A2is the type 2adversary respectively）is a polynomially－bounded adversary against a ciphertext with advantageε，makes at most qHque－ries to the hash functions H，and makes qDqueries to the decryption oracles respectively．Then we show how to construct two types adversary A1and A2．We can assume that challengers C1and C2for both types of games are available to algorithm B who can break the scheme．Then there exists a polynomiallybounded algorithm C that solves the BDH problem with advantage at least

Proof：Suppose that the algorithm C （the challenger）is given for a random instance of BDH problem as（g，ga，gb，gc）．The algorithm C’s task is to output e（g，g）abcfor some a，b，c∈Z＊pafter interacting with B as follows：

B begins by choosing some random bits c and I，J uniformly at random with 1≤I，J≤qH．If c＝0，then B chooses to play against C1and aborts C2．When c＝1，B chooses to play against C2and aborts C1．In either case，C＝ （C1，C2）will denote the challenger against B which plays for the remainder of this proof．

Here，we let R denote the event IDIand IDJas the challenge identities IDchand IDch＇．We denote the event that A extracts the partial private key for entity IDI，IDJas F0and denote the event that A replaces the public key of identity IDIand IDJas F1at some points in its attack．If c＝0and the event F0occurs，B will have to abort and will be unsuccessful．If F0does not occur and if the event R occur，then B will be successful with some probability related to that of A1．Besides，if c＝1and the event F1occurs，B will again abort and will be unsuccessful．If F1does not occur，but R occurs，the probability of B’s success will again be related to that of A1．

If c＝0，then C is equivalent to Type 1challenger and supplies B with public parameters Parms＝ ＜G，G1，e，H，g，p，＞．If c＝1，C is a type 2challenger and supplies B with public parameters parms with the master secret key s and ppub＝gs．

B has controlled over the hash function H．To respond to the hash queries，C maintains a hash list LHthat stores information on H－queries．This list is initially empty．

Assume the H－queries are distinct and that any query involving an IDiis preceded by the H－query for IDi．

Phase 1：B responds to A’s queries as follows：

Setup：C runs algorithm Setup，outputs the system parameters＜G，G1，p，e，g，ppub，H ＞．

Public Key Extract query：Upon receiving apublic key query for any identity ID，C computes the corresponding public key PKIDand sends it to A and then adds it to the list LPK．

H－queries：When A asks a polynomial bounded number of H－queries on identities of his choice．B responds as follows．

（1）If IDior IDjalready appears on the LHlist such as the form ＜IDi，PKi，Qi，bi，xi，Xi，Yi＞，＜IDj，pkj，Qj，bj，xj，Xj，Yj＞．B returns H（IDi，pki）＝Qior H（IDj，pkj）＝Qjto A．

（2）IFIDior IDjdoes not already appear on the list LHand is the I－th or J－th distinct H query made by A，then B chooses bI，bJat random from，outputs H（IDi，PKi）＝bIQ，H（IDj，PKj）＝bJQand adds the entry＜IDI，PKI，bIQ，bI，⊥，X，Y ＞，＜IDJ，PKJ，bJQ，bJ，⊥，X，Y ＞into the list LH．

（3）If IDior IDjis the i－th or j－th distinct H－query where i≠I，j≠Jand IDi，IDjdoes not appear on the list LH，B chooses random values bi，bj，xi，xj∈，outputs H（IDi，PKi）bi，H（IDj，PKj）＝bjand adds＜IDi，PKi，bi，bi，xi，gxi，（ppub）xi＞，＜IDj，

From above we can see that the partial private key for IDi（i≠I）or IDj（j≠J）is equal to（ppub）bior（ppub）bjrespectively，the public key isand the private key isWhen c＝0，these can be computed by B．When c＝1，B can compute the partial private key gsbIQfor the identity IDIand compute the partial private key gsbJQfor the identity IDJ．

Notice that we assume that A always makes the appropriate H query on the identity IDi，IDj，before making one of these requests．B replies to these requests as follows．

Partial Private Key Extract：When A requests for the identity IDior IDj，there are several cases：

1．If i＝Iand c＝0or j＝Jand c＝0，then B aborts．

2．If i＝Iand c＝1or j＝Jand c＝1，then B returns with gsbIQor gsbJQ．

3．If i≠Ior j≠Jthen B replies with

Private Key Extraction：When A requests for the identity IDior IDj，and we assume that the public key for IDi，IDj，has not been replaced．Then we have：

1．If i＝Ior j＝J，then B aborts．

Replace Public Key：When the request is to replace the public key for IDior IDjwith value＜X′i，Y′i＞

1．If i＝Iand c＝1or j＝Jand c＝1，then B aborts．

2．If i＝Iand j＝Jand c＝0，then B aborts．

3．Otherwise，B replaces the current entries Xi，Yiin the LHlist with new entriesor replaces the current entries Xj，Yjin the LHlist with new entries

Re－Encryption Key Extraction：When A queries C about re－encryption key RKIDi－IDj，andi＝Iandj＝J，C rejects．Otherwise，C first generates a CLE public key PKIDi，and then checks the list LH，if the checked identity IDiand IDjare in the list，then C returns the secret values xi，xjto B respectively．Then B computes the re－encryption key as the above scheme．If the checked identity is not in the list LH，C runs the H random oracle to generate the corresponding secret value and returns them to B and adds them into the list LH．

Re－Encryption Queries：Suppose that A queries C about（IDi－IDj，CIDi）for encryption，if IDi（i≠I）and IDj（j≠J）have never been requested for the private key extract query rejects the query．Otherwise，C runs private key extraction to generate skIDi，skIDj，and then C computes the re－encryption key RKIDi－IDjas above algorithm．When c＝0，if both of the two identities IDiand IDjmake queries for the public key replace at the same time，then C rejects．Finally C re－encrypts CIDiinto CIDjby running re－encryption algorithm and C returns CIDjto B．

Decryption Queries：When adversary A requests for decryption for the ciphertext＜U，V＞for IDi（Notice that i is an arbitrary value between 1and qH）and the private key is just the one corresponding to the current value of the public key for IDi．But wheni＝Ior i＝J，B cannot make use of C to reply the request，otherwise，C decrypts the ciphertexts and returns the plaintext to B．

Challenge Phase：In this phase，A chooses the challenge identity IDch，IDch＇and two plaintexts m0，m1on which it wishes to be challenged．Assume that the challengers’identities have already been requested of random oracle H but that A1has not extracted the partial private key and replaced the public key for the identities IDchand IDch＇．Then we have：If IDch≠IDIor IDch＇≠IDJthen B aborts．Otherwise，if IDch＝IDIand IDch＇＝IDJ，then B gives C m0，m1that will be re－encrypted．C chooses b∈ ｛0，1｝，encrypts mb，then responds with the challenge ciphertextand re－encrypts ciphertext CIDI＊ ＝＜UI＊，by making use of the re－encryption key RKIDI－IDJ，finally sends it to B．

Phase 2：B continues to response to A’s requests in the same way as it did in Phase 1．The restriction on A’s behavior is reflected in this phase．

Guess：Eventually，A outputs its guess b′．If b′＝b，a wins，otherwise，A loses．

Analysis：If B does not abort during the simulation，then the probabilityeasy to see that B’s responses to hash function H is uniformly and independently distributive．Provided B does not abort then all responses to A’s requests are valid．Moreover，the challenge ciphertexts CI＊Dll∈｛I，J｝is a valid encryption of mbunder the current public key for identity IDIor IDJ．Therefore，we have that

Now we examine the probability that B does not abort during the simulation．It is easy to see that B can abort for one of several reasons：

（i）When c＝0and the event F0occurred during the simulation．

（ii）When c＝1and the event F1occurred during the simulation．

（iii）When A made a private key extraction on IDior IDJat some point．

（iv）When A chooses IDch≠IDIor IDch＇≠IDJin challenge phase．

（v）When A made the decryption query on the challenge ciphertext CIDI＊ ＝

（vi）Both of the two challenge identity IDIand IDJcan be made queries for the public key replace at the same time．

Now we analyze the probability．As the description in literature［2］，here we name the event（c＝i）∧Fias Rifor i＝0，1．We name the third，the fourth，the fifth and the sixth event as F2，F3，F4，F5．It is easy to see that the event F3is just the event⇁Reassume A makes q1queries of H and chooses the identity IDch，IDch＇from the responses IDi，IDj．Because B’s choice of the identity is random uniformly from the set of q1indices i，j．So the probability of IDch＝IDI，IDch＇＝IDJis equal tBecause the event⇁F3implies the event⇁F2，namely，the event R happen must lead to the event⇁F2 happen．Moreover，the event R0and R1are mutually exclusive．And the probability of the event F5happen is．In a similar way，we have：Pr［B does not abort］

Because Fiand c＝i are mutually independent，so we have：

Because again R0and R1are mutually independent，moreover if the event R happens，it must lead to the event F4not happen，and if the event R happens，it must lead to the event F5not happen，so we have：

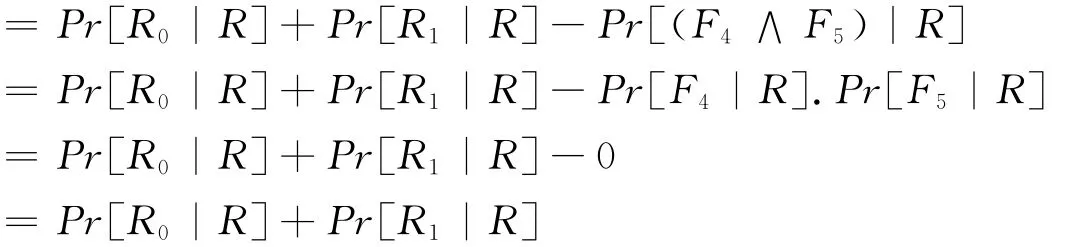
Because R and Ri（i∈ ｛0，1｝）are mutually independent＝i and R are mutually Independent，Fi｜Ris independent of the event c＝i．So：

So we have：

Pr ［B does not abort］

Finally，because Pr［F0∧F1｜R］＝0，from the following derivation

we can see that：Pr［F0｜R］＋Pr［F1｜R］≤1．So we have that：

Similarly，it is easy to see that B’s advantage is at leastThis completes the proof of the theorem．

［1］ Mambo K．Poxy cryptosystems：delegation of the power to decrypt ciphertexts［J］．EICE Trans Fund Electr Comm Comp Sci E80－A，1997 （01）：54－63．

［2］ Blaze M，Bleumer G，Strauss M．Divertible protocols and atomic proxy cryptography ［A］．Nyberg K．EUROCRYPT1998 ［C］．Heidelberg：Springer，1998：127－144．

［3］ Jakobsson M．On quorum controlled asymmetric proxy re－encryption ［A］．Imai H，Zheng Y．PKC1999 ［C］．Heidelberg：Springer，1999：112－121．

［4］ Dodis Y，Ivan A．Proxy cryptography revisited ［A］．Proceedings of the 10thAnnual Network and Distributed System Security Symposium－NDSS’03［C］．San Diego：IEEE Conference Publications，2003：80－89．

［5］ Zhou L，Marsh MA，Schneider FB，et al．Distributed blinding for ElGamal re－encryption Technical Report 2004－1924［Z］．Cornell University，NY USA，2004．

［6］ Ateniese G，Fu K，Green M，et al．Improved proxy re－encryption schemes with application to secure distributed storage ［A］．Proceedings of the 12thAnnual Network and Distributed System Security Symposium－NDSS’05［C］．San Diego：IEEE Conference Publications，2005：83－107．

［7］ Green M，Ateniese G．Identity－based proxy re－encryption ［DB／OL］．Http：／／eprint．iacr．Org／2006／473．

［8］ Matsuo T．Proxy re－encryption systems for identity－based encryption ［A］．Takagi T．et al．Pairing 2007，LNCS［C］．Heidelberg：Springer，2007：247－267．

［9］ Verheul E．Evidence that XTR is more secure than supersingular elliptic curve cryptosystems［A］．Advances in Cryptology－Eurocrypt 2001，LNCS ［C］．Berlin：Springer－Verlag，2001：195－210．

［10］ Boneh D，Franklin M．Identity－based encryption from the Weil Pairing．Extended abstract［DB／OL］．http：／／crypto．stanford．edu／～dabo／abstracts／bfibe．html．

Certificateless Proxy Re－encryption Scheme from Pairings

WANG Hui－ge，CAO Hao，LIU Bin，SHEN Feng
（School of Science，Anhui Science and Technology University，Fengyang 233100，Anhui，China）

The concept of proxy re－encryption was introduced by Mambo and Okamoto．Its function takes a ciphertext for a message encrypted under an identity’s public key and transforms it into a ciphertext for the same message under another identity’s public key．But these schemes were generally based on PKC or ID－based cryptosystem．We present a new proxy reencryption scheme based on certificateless public key cryptosystem．Our scheme has advantages over prior schemes．It can realize multi－use property．The algorithm of our scheme is simpler than that of other schemes and a CCA proof to this scheme is given．

certificateless；proxy encryption；re－encryption；proxy re－encryption

TP 039

A

10．3969／j．issn．1673－1492．2012．04．010

来稿日期：2011－01－10

Higher School of Provincial and Outstanding Youth Talent Fund Project［2012SQR141］；Natural Science Foundation of Anhui Educational Committee，No．KJ2010B059

王会歌（1981－），女，河南许昌人，安徽科技学院理学院教师，硕士。

刘守义 英文编辑：刘彦哲］