提取准双周和准一月低频振荡的Lanczos滤波器及其应用

姚菊香，李丽平，罗璇，杨玮，王盘兴

(南京信息工程大学大气科学学院，江苏南京210044)

0 引言

自从Madden and Julian(1971，1972)发现热带大气的纬向风和气压场存在40～50 d周期的低频振荡(LFO)以来，大气中的低频振荡现象一直受到气象学家高度重视。对于低频振荡的重要性，国内外学者做过较为系统总结(李崇银，2004;Zhang，2005)。青藏高原热力作用对中高纬度地区低频振荡的产生具有重要作用(章基嘉等，1991;刘式适等，2000)。通过1979年第一次青藏高原气象科学试验，章基嘉等(1984)发现高原热源分量存在中周期(4～10 d)、短周期(2～3 d)的振荡;周兵等(2000)指出高原东部地面感热通量存在30～50 d低频振荡和准双周振荡。

徐国强和朱乾根(2000)在分析1998年高原大气低频振荡结构特征时指出，高原存在多尺度的大气低频振荡，高原和长江中下游的低频降水存在同时加强和同时减弱的关系。巩远发等(2007)指出，2001和2003年夏季的亚洲季风区，夏季5—8月期间，高原中南侧较强的低频热源(热汇)对后期江淮流域降水偏多(少)起重要作用。王跃男等(2009)指出1978(1999)年夏季青藏高原东部大气热源存在以10～20 d(30～60 d)周期为主的振荡，并与长江中下游降水在10～20 d(30～60 d)频段存在显著相关。

上述研究发现，青藏高原热源存在多时间尺度特征，并对东亚大气环流、中国气候变化以及灾害性天气的形成和发展有着重要的影响。为了更好地研究高原季内振荡的多尺度特征，一个优良的滤波器是必要的。姚菊香等(2005)以30～60 d低频振荡为对象，定量分析了常用的Butter worth带通滤波器(Murakami，1984;简记为B.f.)和Lanczos带通滤波器(Duchon，1979;简记为L.f.)性能的优劣，结果表明，对于取样间隔为1 d的序列，当L.f.滤波器参数l≥69时，其滤波性能全面优于B.f.。本文的目的是根据青藏高原大气热源季内振荡分析的实际需要，讨论两个波段(10～20 d、20～40 d)L.f.的滤波特性，确定L.f.滤波器临界参数，并以拉萨附近格点1950—2006年逐年整层热源日序列为例，验证两个波段L.f.功能，为高原及邻近区域热源季内振荡及传播特征研究提供基本方法。

1 Lanczos滤波器

Lanczos滤波器(L.f.)是一种数字滤波器(Duchon，1979)。对采样间隔Δt=1 d的时间序列

要滤出频段［f1，f2］的分量，需要先计算L.f.的权重函数Lw(τ):

它由2l+1个数构成(l为L.f.的参数)。通过

可从序列(1)中滤出频段［f1，f2］的分量;滤波过程使序列(1)缩短2l(单位:d)。(3)式中“*”为卷积算符。

L.f.的频率响应函数为

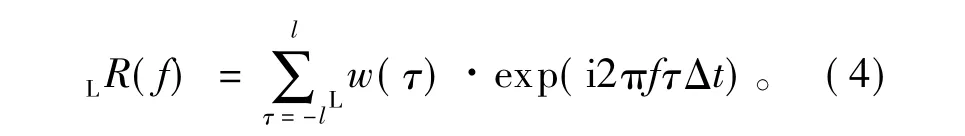
理想滤波器的响应函数记为R(f)(燃料化学工业部石油地球物理勘探局计算中心站，1974)。

图1和图2分别给出了提取10～20 d与20～40 d两个波段的L.f.的响应函数LR(f)与R(f)的

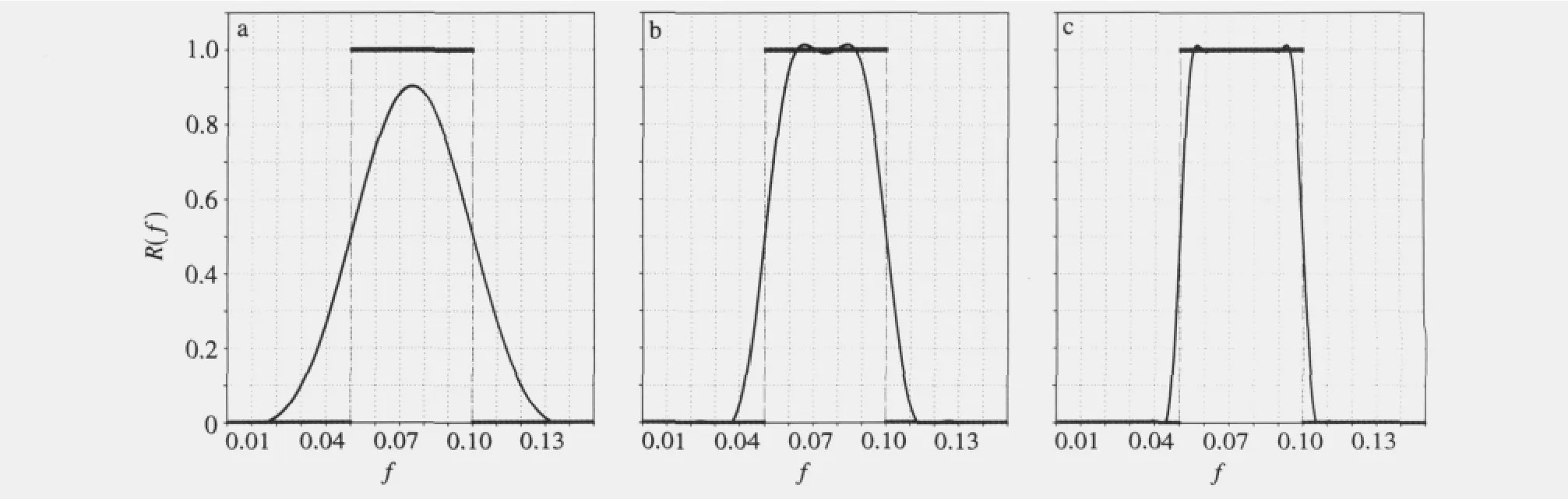
图1 提取10～20 d振荡的L.f.的响应函数LR(f)与理想滤波器响应函数R(f)的比较(曲线、粗实水平线分别为LR(f)、R(f))a.l=20;b.l=50;c.l=121Fig.1 Comparison of the response functionLR(f)of L.f.for filtering 10—20 d oscillation and the response function R(f)of ideal filter(The curve and thick solid horizontal line indicateLR(f)and R(f)filters，respectively)a.l=20;b.l=50;c.l=121

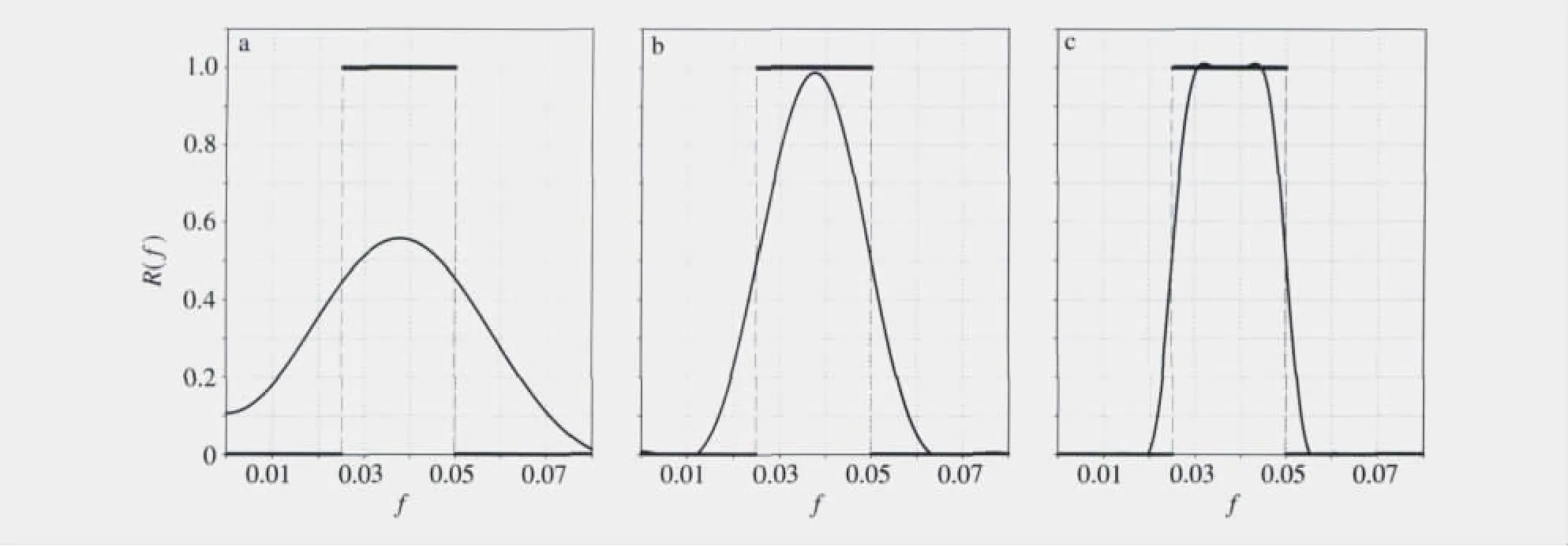
图2 提取20～40 d振荡的L.f.的响应函数LR(f)与理想滤波器响应函数R(f)的比较(曲线、粗实水平线分别为LR(f)、R(f))a.l=20;b.l=50;c.l=121Fig.2 Comparison of the response functionLR(f)of L.f.for filtering 20—40 d oscillation and the response function R(f)of ideal filter(The curve and thick solid horizontal line indicateLR(f)and R(f)filters，respectively)a.l=20;b.l=50;c.l=121

比较。可见，随着l的增大，LR(f)趋向于R(f)。其中:

2 L.f.滤波效果的定量分析

2.1 L.f.、B.f.和H.f.三种滤波器响应函数的比较

判断L.f.滤波效果的优劣，可以通过比较它与Butter worth滤波器(B.f.)、谐波滤波器(H.f.)(冯康，1978)的响应函数进行。B.f.与H.f.都是分析季内振荡常用的滤波器，它们的频率响应函数分别记为BR(f)、HR(f)。

B.f.是频率连续型滤波器。从序列(1)中滤出频段［f1，f2］的B.f.的频率响应函数为

其中，Z、a、b1、b2取决于Δt、f、f1、f2的值的大小。通过

从序列(1)中滤出频段［f1，f2］的分量。滤波不改变序列的长度。

H.f.是频域(或周期域)上的离散型滤波器(冯康，1978)。对(1)式的序列，有谐波分解式

式中:ak、bk是波数k的余弦、正弦谐波波数;Δf=

1/n(d－1)是基频。从(1)式中滤出的H.f.的频率响应函数为

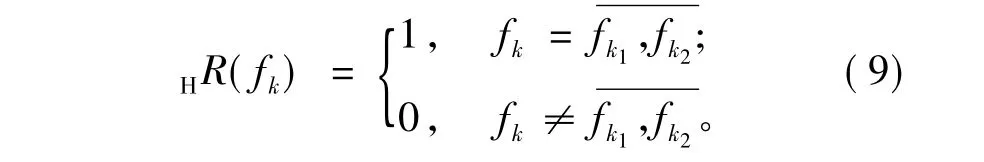
滤波结果为

与B.f.类似，H.f.滤波也不改变序列的长度。

图3给出了提取夏季(n=92)中10～20 d、20～40 d波段(分别记为a、b波段)的B.f.、H.f.的频率响应函数BR(f)、HR(fk)分别与R(f)的比较。

HR(fk)在fk=k/n上与R(f)相等;BR(f)与R(f)、HR(fk)差异明显。除中心频率f0=上BR(f)达到R(f)外，其余频率上BR(f)均不等于R(f)。

与图1、图2的LR(f)比较，对较小l(图1a、2a)，两波段上的BR(f)较LR(f)更接近R(f)，故B.f.优于L.f.;而对较大l(图1c、2c)，LR(f)较BR(f)更接近R(f)，故在l取值较大时，L.f.优于B.f.。根据表1可知，a，b波段近似可以由的H.f.获得。

2.2 L.f.滤波性能优于B.f.的临界参数l0的确定

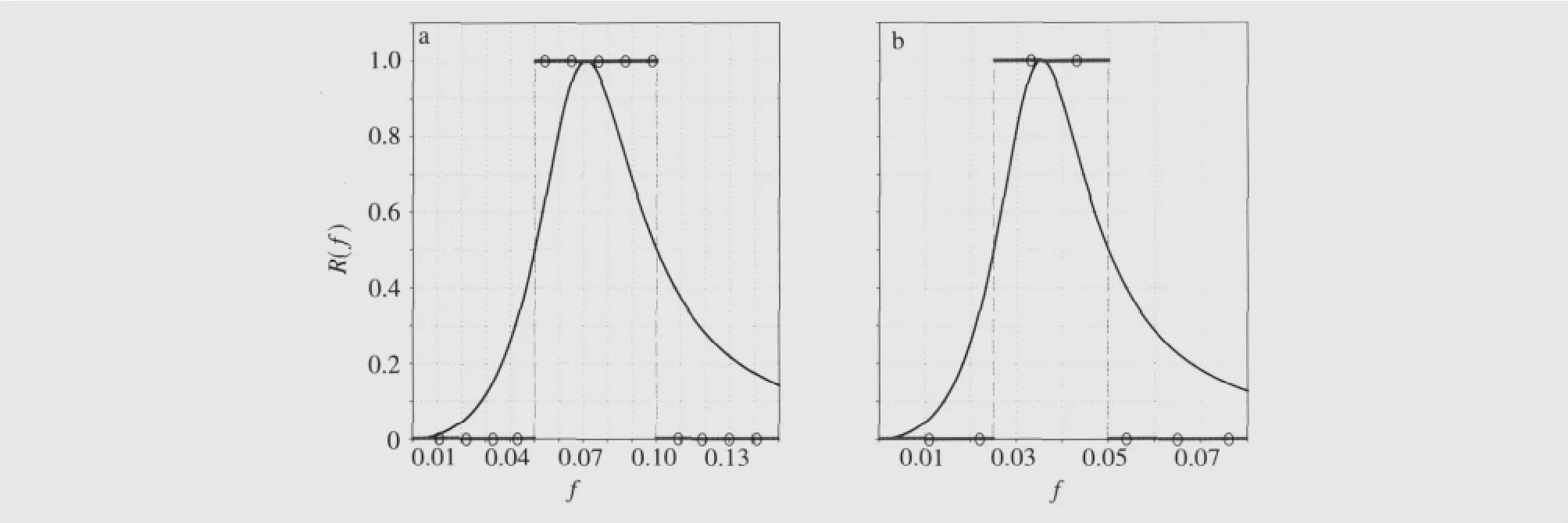
图3 BR(f)、HR(fk)与R(f)的比较(曲线为BR(f)，○为HR(fk)，粗实水平线为R(f))a.提取周期为10～20 d;b.提取周期为20～40 dFig.3 Comparison ofBR(f)，HR(fk)and R(f)(The curve indicatesBR(f)，○indicatesHR(fk)，and the thick solid horizontal line indicates R(f))a.the period of 10—20 d;b.the period of 20—40 d

表1 序列(1)的k=0，10的周期Tk和频率fk(n=92)Table 1 Period Tkand frequency fkof time series(1)for k=n=92)

表1 序列(1)的k=0，10的周期Tk和频率fk(n=92)Table 1 Period Tkand frequency fkof time series(1)for k=n=92)

k 012345678910 Tk/d∞92.046.030.723.018.415.313.111.510.29.2 fk/d－100.0110.0220.0330.0430.0540.0650.0760.0870.0980.109

率区间［0 d－1，0.5 d－1］分为3段:通过带［f1，f2］、低频抑制带［0，f1)、高频抑制带(f2，0.5 d－1］，分别以i=标记;则L.f.与B.f.在通过带、低频抑制带、高频抑制带的输出输入方差比分别为

和

由此，对提取频段［f1，f2］的滤波器，可定义L.f.与B.f.在通过带和两个抑制带上的滤波效率比(以下简称效率比)为

它是确定L.f.滤波性能超过B.f.的l临界值的统计量。

表2和表3给出了a、b波段L.f.与B.f.的两种效率比随l的变化。由ir(l)定义知，1r(l)＞1表示L.f.滤出带性能优于B.f.;2r(l)＜1、3r(l)＜1表示L.f.抑制带性能优于B.f.。故当1r(l)＞1和2r(l)、3r(l)＜1均得到满足时，L.f.滤波效果全面优于B.f.。

由表2和表3可见，10～20 d和20～40 d波段L.f.的l临界值l0分别为24、46;当l≥l0时，L.f.的滤波效果必定优于B.f.。

3 应用举例

以拉萨夏季整层热源(100 hPa至地面)准双周和准一月振荡分析为例，验证L.f.的应用。

3.1 资料和滤波

Zhang et al.(2009)用NCEP/NCAR逐日再分析资料(Kalnay et al.，1996)，按Yanai et al.(1992)倒算法求得了全球1948—2006年逐日大气热源数据集。本文取格点(90°E，30°N)1950—2006年的序列代表拉萨(91.13°E，29.67°N)整层热源，记为

表2 10～20 d L.f.与B.f.的效率比ir(l)Table 2 The efficiency ratioir(l)for L.f.and B.f.of 10—20 d

表3 20～40 d L.f.与B.f.的效率比ir(l)Table 3 The efficiency ratioir(l)for L.f.and B.f.of 20—40 d

称它为ty年年序列;t'为年日序，年总日数n'=365(平年)或366(闰年)。

从(14)式中提取序列

称它为ty年夏季序列;td为夏季日序。

使用L.f.(参数l取121)从(14)式的年序列中求得夏季a、b波段(即10～20 d，20～40 d波段)振荡分量。a、b波段滤波结果记为

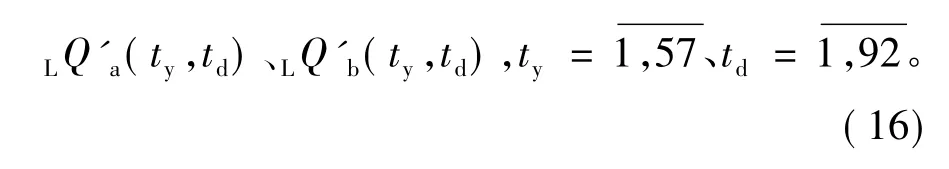
相应地，使用H.f.直接从夏季序列((15)式)中求得a、b波段振荡分量

以1959年为例，对两个波段L.f.的滤波结果与谐波分析结果进行比较。图4给出了1959年夏季的Q及由(17)、(18)式给出的a、b波段LQ'、HQ'。

图4 拉萨1959年夏季整层热源及滤波结果(图4a中水平线为¯Q(1959)=79.5 W·m－2;图4b、c中实线分别为LQ'a和LQ'b，虚线分别为HQ'a和HQ'b;单位:W·m－2)a.Q;b.LQ'a和HQ'a;c.LQ'b和HQ'bFig.4 The whole heat source and its filtering results over Lhasa in summer 1959(The horizontal line indicates¯Q(1959)=79.5 W·m－2in Fig.4a;The solid lines indicateLQ'aandLQ'b，and the dashed lines indicateHQ'aandHQ'bin Fig.4b and Fig.4c，respectively;units:W·m－2)a.Q;b.LQ'aandHQ'a;c.LQ'bandHQ'b

由图4可知，通过L.f.滤波得到的a、b波段振荡分量与谐波分析的结果非常接近。

3.2 a、b频段振荡强度分析

用(16)、(17)式的资料定义了ty年a、b频段的振荡强度，即它们是ty年夏季a、b频段振荡的日均方差。图5给出了它们的年际变化曲线。可见，LE、HE做准同步变化;a、b频段振荡存在明显的年际变化。

由图4和图5可知，两个波段L.f.的滤波结果在加热季内变化与波段能量年际变化两方面均与相应谐波分析接近，由此可以说明，选用l=121的L.f.可以很好地滤出逐日热源序列中的10～20 d与20～40 d振荡。l=121的L.f.滤波结果可用于青藏高原大气加热季内振荡的实际分析。

表4据LEa(ty)、LEb(ty)值列出了a、b频段的6个最强年。

3.3 a、b频段的振荡过程

图5 拉萨1950—2006年a、b频段振荡强度的年际变化(实线为LEa、LEb;虚线为HEa、HEb;单位:104W2·m－4;1970年LEa、LEb缺损)a.LEa和HEa;b.LEb和HEbFig.5 The interannual variations of oscillation intensity in a and b frequency ranges in Lhasa from 1950 to 2006(The solid lines indicateLEaandLEb，and the dashed lines indicate HEaandHEb;units:104W2·m－4;In 1970，theLEaandLEbis deficient)a.LEa andHEa;b.LEbandHEb

图6 拉萨a、b频段振荡强年振荡过程(单位:102W·m－2)a.LQ'a(1997，1988，1967年);b.LQ'b(1968，1959，1960年)Fig.6 The oscillation processes in the strong oscillation years in a and b frequency ranges in Lhasa(units:102W·m－2)a.LQ'a(in 1997，1988 and 1967);b.LQ'b(in 1968，1959 and 1960)

表4 拉萨1950—2006年夏季a、b频段振荡的最强年份Table 4 The strong oscillation years in a and b frequency ranges in Lhasa in summer from 1950 to 2006

利用(16)式的LQ'a、LQ'b，可以分析拉萨夏季a、b频段的振荡过程。图6给出了a、b频段振荡3个最强年振荡过程。可见，1997、1988年a频段振荡均在7月上旬前后达最强，且1988年8月中、下旬还有一次较强过程;而1967年a频段振荡在7月中、下旬前后最强。1968、1959年b频段振荡分别在7月上旬、6月中旬前后最强，而在1960年强振荡则从6月上旬一直维持至8月上旬间。因此，拉萨夏季热源a、b频段振荡过程存在明显的年际差异和多样性。

4 结论

根据青藏高原大气热源季内振荡分析的实际需要，设计了适于提取准双周(10～20 d)、准一月(20～40 d)振荡的Lanczos滤波器(L.f.)。通过与Butterworth滤波器(B.f.)滤波效果的定量分析，确定了准双周、准一月L.f.窗宽参数l的临界值l0=24、46;当l≥l0时，L.f.滤波器性能全面优于B.f.。

选用拉萨附近格点(90°E，30°N)的1950—2006年整层大气热源资料Q作了应用试验，结果表明，由l=121的L.f.得到的拉萨夏季准双周、准一月振荡分量LQ'a、LQ'b质量可靠，可用于青藏高原大气热源季内振荡强度的年际差异和季内过程分析。

致谢:张博、陈隆勋先生提供了拉萨整层大气热源资料，谨致谢忱。

冯康.1978.数值计算方法［M］.北京:国防工业出版社.

巩远发，段廷扬，张菡.2007.夏季亚洲大气热源汇的变化特征及其与江淮流域旱涝的关系［J］.大气科学，31(1):89-98

李崇银.2004.大气季节内振荡研究的新进展［J］.自然科学进展，14(7):734-741.

刘式适，柏晶瑜，徐祥德，等.2000.青藏高原大地形的动力、热力作用与低频振荡［J］.应用气象学报，11(3):312-321.

彭永清，王盘兴，吴洪宝.1997.大气低频变化的分析与应用［M］.北京:气象出版社.

燃料化学工业部石油地球物理勘探局计算中心站.1974.地震勘探数字技术:第二册［M］.北京:科学出版社.

王跃男，陈隆勋，何金海，等.2009.夏季青藏高原热源低频振荡对我国东部降水的影响［J］.应用气象学报，20(4):419-427.

徐国强，朱乾根.2000.1998年青藏高原大气低频振荡的结构特征分析［J］.南京气象学院学报，23(4):505-512.

姚菊香，王盘兴，李丽平.2005.季节内振荡研究中两种数字滤波器的性能对比［J］.南京气象学院学报，28(2):248-253.

章基嘉，彭永清，王鼎良.1984.夏季青藏高原各热源分量的时频特征及高度场对它们的响应［C］//青藏高原气象科学实验文集(一).北京:科学出版社:182-192.

章基嘉，孙国武，陈葆德.1991.青藏高原地区的大气低频振荡［M］.北京:气象出版社.

周兵，何金海，徐海明.2000.青藏高原气象要素场低频特征及其与夏季区域降水的联系［J］.南京气象学院学报，23(1):93-100.

Duchon C E.1979.Lanczos filtering in one and two dimensions［J］.J Appl Meteor，18(8):1016-1022.

Kalnay E，Kanamitsu M，Kistler R，et al.1996.The NCEP/NCAR 40-year reanalysis project［J］.Bull Amer Meteor Soc，77(3):437-471.

Madden R A，Julian P R.1971.Detection of a 40-50 day oscillation in the zonal wind in the tropical Pacific［J］.J Atmos Sci，28(5):702-708.

Madden R A，Julian P R.1972.Discription of global-scale circulation cells in the tropics with a 40-50 day period［J］.J Atmos Sci，29(6):1109-1123.

Murakami M.1984.Analysis of deep convective activity over the western Pacific and southeast Asia.Part II:Seasonal and in traseasonal variation during the northern summer［J］.J Meteor Soc Japan，62(1):88-108.

Yanai M，Li C，Song Z S.1992.Seasonal heating of the Tibetan Plateau and its effects on the evolution of the Asian summer monsoon［J］.J Meteor Soc Japan，70(1):319-350.

Zhang Bo，Chen Longxun，He Jinhai，et al.2009.Characteristics of atmospheric heat sources over Asia in summer:Comparison of results calculated using multiple reanalysis datasets［J］.Acta Meteor Sinica，23(5):585-597.

Zhang C.2005.Madden-Julian Oscillation［J］.Reviews of Geophysics，43，RG2003.doi:10.1029/2004RG000158.