网格尺寸及边界对大地电磁有限元正演精度的影响

吴 娟，席振铢，王 鹤

（中南大学 地球科学与信息物理学院，湖南 长沙 410083）

0 前言

有限元作为一种高效的数值模拟方法，由于不需要考虑物体的内部边界条件，而被广泛应用于地球物理的正演计算。作为大地电磁的数值模拟，最早是由Coggon［1］于1971年引入的。此后Wannamaker［2］、Mitsuhata［4］、徐世浙［5］、李予国［6］、阮百尧［7］、王绪本［8］等，相继对有限元的二维三维模拟，研究了地形、插值函数以及介质的电导率连续性等问题。随着计算机的不断发展，人们对正演模拟的精度要求越来越高，计算结果的误差直接影响着后续反演的效果。因此，许多学者又从多个方面对有限元的算法加以改进。陈小斌［9］提出了一种新的有限元直接迭代算法，马为［10］等又在此基础上选用二次插值基函数计算辅助场的函数值；张秀敏［11］改进了电磁场计算中大型稀疏方程组的迭代解法；柳建新［12］等将带预处理的双共轭梯度算法运用到带地形电磁的二维、三维正演中，使求解线性方程的精度进一步提高。

在众多的研究中，都只是在有限元的插值函数或者解方程的精度上做了改进，而对于有限元前处理中的细节问题，讨论得并不多。众所周知，有限元研究区域的尺寸问题，直接影响到正演计算的精度和速度，由网格剖分的不合理性所导致的误差，远大于解方程所引起的误差。如果网格剖分得不够合理，那么再高精度的求解系统，也得不到正确的解。由于矩形网格线性插值在求解地球物理问题中具有典型的代表性，因此，作者在具体研究了矩形网格双线性插值中网格尺寸以及边界条件对计算结果的影响后，总结出相应规律，以供后续计算。

1 变分问题

构造如图1所示（见下页）坐标系。

有限元解大地电磁二维问题的边值问题为：

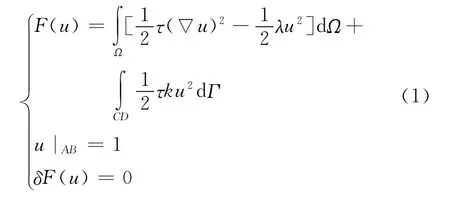
图1 大地电磁有限元模拟研究区域及坐标Fig.1 Study area and coordinates for MT modeling use finite element method

其中 u代表解线性方程组后得到的节点场值，对于 TE模式：u＝Ez；τ＝1／（iωμ）；λ＝σ。对于 TM模式：u＝ Hz；τ＝iωμ；λ＝1／σ；ω为角频率；σ和μ分别代表介质电导率和磁导率。

经过变分之后，都得到了一个关于有限元系数矩阵的线性方程组，即：Ku＝0，其中K即有限元的刚度矩阵。在计算刚度矩阵时，先要利用插值函数来计算单元系数矩阵Ke，而等参单元的插值基函数，其系数不仅与单元的节点坐标相关，而且与单元的宽度和高度相关。

在求解线性方程组时，要带入边界条件，其中内部边界条件在泛函取极值的过程中自动满足，属于自然边界条件，将不予考虑。剩下就是外边界条件，即：

一般的处理是，对于上边界AB，由于电磁波在空气中几乎不衰减，要使异常场在边界上的偏导数为零，就必须把其放置在无穷远，这样就可以令u＝1。对于左右边界，也采取同样的方式。而对于下边界，同样也要使异常场在边界上产生的值为零，由于下边界以下为均匀半空间，因此，它所满足的边界条件为第三类边界。

求解方程组，得到各个节点的场值之后，还必须求得相应的视电阻率值：

在计算偏导数时，可以采取二点差分公式，也可以采用三点差分公式或者更高次的差分公式。为了提高视电阻率精度，作者在本文中采用了四点差分公式。取近地表的连续的四个节点，为了计算方便，一律把位于近地表一层连续的四个节点采用等距剖分，ui、ui＋1、ui＋2、ui＋3分别代表从地表连续向下分布的四个节点，则：

其中 l是四个节点之间的距离，带入公式（3）、公式（4）中，就能得到TE和TM模式下的视电阻率了。

从公式（5）中，我们可以得出以下结论：

（1）采用四点差分格式计算微分时，必须是等步长，也即地表以下连续三个网格必须为相同的间距。

（2）偏导数的值与网格步长息息相关，即网格剖分的疏密程度将直接影响着计算结果的精度。

根据有限元满足的边界，又必须将网格边界设置在无限远处，这样必将增加计算量。那么，究竟如何选择合适网格参数来既保证计算精度又不太消耗计算机内存呢？网格的边界取值的远近是否会影响计算结果呢？下面将具体从边界影响和网格横、纵网格步长三个方面来讨论。

图2 一维和二维介质模型图Fig.2 One－dimensional and two－dimensional models

2 模型计算

2.1 左右边界的影响

为了研究左右边界对计算结果的影响，作者分别以均匀半空间、水平层状介质和二维的低阻嵌入体模型为例，模型如图2所示。

其中，均匀半空间电阻率为100Ω·m。采用30（纵）×32（横）的网格，横纵单元均为等距剖分，网格步长均为10m。在此基础上，令横向第一个和最后一个网格的左右边界，分别为±160m、±500m、±1km、±10km、±100km，频率范围从10－3Hz～103Hz，对数等间距分布21个频点，所得视电阻率测深曲线如下页图3所示。

在图3（a）中，视电阻率的幅值在100Ω·m附近，最大误差不超过0.5%，由此验证了程序的正确性。结合图3（b），在左右边界不断延伸的过程中，其数值模拟的结果也与解析解十分吻合，由此可以看出，左右边界对均匀和一维介质几乎没有影响，因此，可以不用将左右边界设置在无穷远处。

图3（c）中的二维介质，由于没有解析解，特给出一个参考解。根据有限元基本理论，当研究区域无限大，网格足够细时，任何一个模型都能得到一个近似的真解。以此为依据，对于尺寸为200m×100m，埋深为100m的低阻嵌入体，将左右边界设置在±100km处，下边界设置在－10km处，网格60（纵）×62（横），以横向±150m和纵向0m～－250m范围为目标区，采用5m的步长等距剖分。由于频率最高为103Hz，趋肤深度为160m，因此5m的步长可认为足够细。在目标区域以外，步长逐渐放大，直至网格的边界，由此解出的数值解定为二维介质的参考解。

在图3（c）中，随着边界的不断扩大，其曲线中段的幅值总体向上抬升，但曲线的起点和终点却没有移动，曲线的基本形态没有变化。我们可以这样解释，对于同样的200m×100m的低阻嵌入体，在左右边界不断扩大的过程中，其围岩的范围也就扩大了。相对而言，模型尺寸与周围的围岩比例就缩小了，而由于视电阻率测深曲线，是地下介质体的综合反映，因此，曲线的幅值也就有所偏向围岩。但当边界为500m以上时，曲线形态基本和参考解重合，由此可见，当边界为目标体尺寸五倍以上时，就可以显著削弱边界条件的影响了。

纵观图3地表视电阻率的计算，其左右边界并不需要取到无穷远处。虽然对于二维体，不同边界的曲线并没与参考解完全重合，但它所反映的浅层和深部的视电阻率信息与实际是没有区别的，而且对于曲线形态的改变并没有质的影响。这是由于在泛函取极值的过程中，要使得异常场在左右边界上的法向偏导数的值为零的真正目的，是为了消去变分过程中左右边界的积分项，使得计算更为便捷。而实现这一目的最简单的方式，就是让边界取到无穷远。然而，对于图3所示的介质和模型，都是关于左右对称的，由于其特殊的对称性，使得其在边界上的影响总是大小相等方向相反的，这样一来，使得函数在边界上的积分和为零，自然满足条件。因此，可以得到这样的结论，即对于左右对称良好的介质，其左右边界并不需取到无穷远。

图3 左右边界对MT计算精度的影响Fig.3 Effects of left and right boundary on accuracy of MT

2.2 边界的影响

为了研究下边界对MT计算精度的影响，作者仍然以模型1和模型2为例。网格仍然采用30（纵）×32（横）的剖分方式，横纵网格分别为均匀剖分，步长10m，此时最后一个网格所示下边界为地表以下260m。在此基础上，分别让最后一层的网格边界改为500m、1km、5km，所得视电阻率曲线如图4所示。

在图4中，层状介质四条不同底边界的曲线与解析解吻合良好。低阻嵌入体同样也引入和2.2节中相同的参考解，不同底边界的响应和参考解也十分吻合。这也就表明，下边界的远近，并不会影响大地电磁的计算精度。

2.3 横向网格尺寸的影响

为了研究横向网格尺寸对计算结果的影响，作者分别以均匀半空间100Ω·m、模型1和模型2为例，采用30（纵）×32（横）的网格，横纵单元均为等距剖分，纵向网格步长为10m，横向网格分别取单元宽度为100m、50m、20m、10m、2m，相对于单元高度为10m，其横纵比分别为：10／1、5／1、2／1、1、1／5。考虑到左右边界的因素，将水平方向第一个和最后一个网格坐标设为±1km。其相应的视电阻率曲线如图5所示。

图5（a）和图5（b）中的数值模拟解和解析解都对应的十分良好，由此可见，横向网格宽度以及横纵比对均匀介质和一维介质都没有影响。对于图5（c）所对应的模型2，为低阻嵌入体，当左右边界相同的情况下，网格横纵比小于10／1时，都与参考解对应良好。

由此可见，大地电磁的有限元数值模拟，其横向网格的剖分可相对随意些。

2.4 纵向网格尺寸的影响

从上两节得出的结论可知，横向网格对视电阻率结果的影响并不大，对称介质边界的远近对视电阻率的计算影响也很小。那么纵向网格对精度的影响又如何呢？在欧东新［13］等人的研究中提到，对于不同频率的大地电磁测深，不能采用同一条网格体系，在高频时要采用小网格，低频时采用大网格。这主要针对的也是纵向网格的尺寸，却没有给出具体的类比参数。而且对于频带相对广泛的MT正演模拟而言，采用二套网格也较不现实。

众所周知，电磁波在地下传播时，能量是衰减的，衡量其探测能力的一个重要参数，就是趋肤深度：

趋肤深度与电阻率成正比，和频率成反比。显然，当频率越高或电阻率越低时，其探测深度越浅。

在正演模拟的过程中，作者根据公式（5），利用差分来代替微分，以求得地面节点值的偏导数。当频率过高时，如果网格宽度大于一个趋肤深度，显然其精度是不够的。由此可见，一套网格最终决定它的纵向网格剖分的，是其最小的趋肤深度。为分析网格剖分与趋肤深度的相互关系，作者仍然以均匀半空间100Ω·m和模型1为例，分别分析影响规律。

首先，在均匀半空间，采用30（纵）×32（横）的网格。由于计算视电阻率时，要求地表以下四个节点是等步长的，为简单起见，横纵单元均为等距剖分，横向网格步长为10m，左右边界为±1km，频带范围10Hz～105Hz，重点分析高频浅部的情况。由2.2小节计算得出，下边界对计算精度影响不大，由此可见，由纵向网格变化引起的下边界的远近影响可忽略。根据趋肤深度的计算公式，电阻率100Ω·m的介质，当频率达到100kHz时，其趋肤深度约为16m。若分别令剖分步长为2m、4m、8m、16m，相应的纵向网格与趋肤深度之比分别为1／8、1／4、1／2、1／1，可以做出相应视电阻率曲线如图6所示。

在图6中，网格相对于趋肤深度越大，其误差越大，并且其误差随着频率的增高而加大。这可以解释为同样的网格，在低频时远远小于趋肤深度，而在高频，就不小于甚至会大于趋肤深度。在图6中的反映就是10kHz以下的频率，正演结果基本接近真值。对于超高频的100kHz，其趋肤深度为16m，此时用大于1／4个趋肤深度的波长，其视电阻率的最大误差就已超过3%，可见此时已不满足精度要求了。

同样的，从图6中还能发现，尺寸越小精度越高。但一味的追求更小的尺寸，同时也增加了模型的计算量。用1／4个和1／8个趋肤深度步长达到的最大误差，都不会超过1%。由此可见，满足精度要求1%的条件下，一个趋肤深度范围内，用四个网格就可以达到很好的计算要求了，这样既保证了精度，又节省了计算量。当然，此结果只针对于线性插值，当插值函数为二次或者更高次时，则只需要更少的网格数。

对模型1所示的层状一维介质，我们采用频率范围为10－3Hz～103Hz，对应于地表一层为100Ω·m的介质，其趋肤深度最小约为160m。为此我们采用和均与半空间相似的做法，保持横向剖分10m的步长，纵向网格等距剖分，分别为10m、20m、50m和100m，那么其相对于趋肤深度的比值为1／16、2／16、5／16、10／16，并与解析解对比，如图7所示。

在图7中，可以发现仍然和图6一样，当尺寸小时精度高，在小于1／8个趋肤深度范围内计算的结果和解析解对应良好，而当网格尺寸大于5／16时，其计算就开始偏离真值了，而且频率越高，其畸变越明显。分析其原因有二：①因为随着频率的升高，其趋肤深度不断减小，因此对网格的尺寸要求更小；②模型2所示的层状介质，其层厚度为100m，当纵向网格尺寸大于50m时，三个网格的深度就已超过了100m，对于公式（3）、公式（4）所计算的地表节点场值的偏导数，就跨越了物性分界面，因此进一步加大了计算误差。所以，在纵向网格剖分时，还应当注意不但与最小趋肤深度有关，而且地表以下连续三个网格不能跨越物性分界面。

3 结论

（1）针对矩形网格双线性插值的有限单元模拟MT问题，下边界对正演精度影响可忽略；而左右对称的介质，左右边界对正演精度影响不大，故可不用将边界放置在无穷远处。

（2）横向网格宽度以及单元横纵比，对计算结果的影响不大，剖分可相对随意些。

（3）纵向网格的剖分与趋肤深度有密切的关系，对于线性插值，网格步长应小于最小趋肤深度的1／4。

［1］ COGGON G H.Electromagnetic and electrical modeling by the finite element［J］.Geophysics，1971（36）：132.

［2］ WANNAMAKER P E，STODT J A，ROJO L.PW2D－Finite element program for solution of magnetotelluric responses of two－dimensional earth resistivity structure［D］.Univ.of Utah Res.Inst.Rep，ESL，1985.

［3］ WANNAMAKER P E，STODT J A，RIJO L.Twodimensional topographic responses in magnetotellurics modeled using finite elements［J］.Geophysics，1986（51）：2131.

［4］ MITSUHATA Y，UCHIDA T.3Dmagnetotelluric modeling using the T－Ωfinite－element method［J］.Geophysics，2004（69）：108.

［5］ 石明娟，徐世浙，刘斌.大地电磁二次函数插值的有限元法正演模拟［J］.地球物理学报，1997，40（3）：421.

［6］ 李予国，徐世浙，刘斌，等.电导率分块连续变化的二维 MT有限元模拟（Ⅱ）［J］.高校地质学报，1996，2（4）：448.

［7］ 阮百尧，徐世浙.电导率分块线性变化二维地电断面电阻率测深有限元数值模拟［J］.中国地质大学学报，1998，23（3）：303.

［8］ 王绪本，李永年，高永才.大地电磁测深二维地形影响及其校正方法研究［J］.物探化探计算技术，1999，21（4）：327.

［9］ 陈小斌，张翔，胡文宝.有限元直接迭代算法在 MT二维正演计算中的应用［J］.石油地球物理勘探，2000，35（4）：487.

［10］马为，陈小斌，赵国泽.大地电磁测深二维正演中辅助场的新算法 ［J］.地震地质，2008，30（2）：525.

［11］张秀敏，苑津莎，徐永生.电磁场分析中大型稀疏方程组迭代解法的改进 ［J］.华北电力大学学报，2003，30（3）：34.

［12］柳建新，蒋鹏飞，童孝忠，等.不完全LU分解预处理的BICGSTAB算法在大地电磁二维正演模拟中的应用 ［J］.中南大学学报，2009，40（2）：484.

［13］欧东新.计算机精度和网格大小对大地电磁有限单元法正演的影响 ［J］.桂林工学院学报，2007，27（3）：329.