基于Gassmann方程岩石速度倒转现象成因分析

林 凯，钟结麟，贺振华，熊晓军

（1.成都理工大学 油气藏地质及开发工程国家重点实验室，四川 成都 610059；2.四川省煤田地质局 141队，四川 德阳 618000）

0 前言

在过去的二十多年中，岩石物理的研究迅猛发展，有力地促进了利用地震资料进行岩石物理分析技术的发展，这项技术衍生出一门新兴的交叉学科，即地震岩石物理学［1］。地震岩石物理学的核心理论之一就是Gassmann等效介质理论，在此基础上所建立的流体饱和多孔介质理论、气体包裹体模型、喷射流模型、BISQ模型等［2］，极大地丰富了饱和岩石介质的弹性波传播理论。

1951年 Gassmann［2、3］提出了饱和流体岩石弹性模量计算公式，由于该方程仅适用于充分低频的情况（孔隙流体处于静态），所以它能很好地适用于地震资料（＜100Hz），具有重要的实用价值，一直受到研究人员的关注。到目前为止，众多专家和学者利用该方程进行了流体替换和横波估算等方面的研究，取得了丰富的成果［4～12］。

Gregory［13］在恒压条件下，对水、空气混合物饱和岩石（砂岩样）进行了系统测量后，对测试数据进行了不同孔隙度岩石速度变化规律综合分析（如下页图1所示），总结了饱和度变化对沉积岩石弹性参数的影响。对于孔隙度大于25%的高孔隙岩石，测量结果显示部份含水岩石速度明显低于100%含气岩石速度，这是饱和度替换的内容。但是对于任意孔隙度岩石，实验室测试结果都是100%含水岩石速度大于100%含气岩石速度。而作者在应用Gassmann方程进行流体替换中发现，在一定孔隙度条件下，100%含气岩石速度大于100%含水岩石速度，这是一种倒转现象，因此对此现象分析是有意义的。

1 方法原理

1.1 Gassmann等效介质理论

Gassmann假设［14］：①岩石（基质和骨架）宏观上是均质的；②所有孔隙都是连通的；③所有孔隙都充满流体（气、液或混和物）；④研究中的岩石～流体系统是封闭的（不排液）；⑤孔隙流体不对固体骨架产生软化或硬化相互作用等条件下，推导出Gassmann方程：

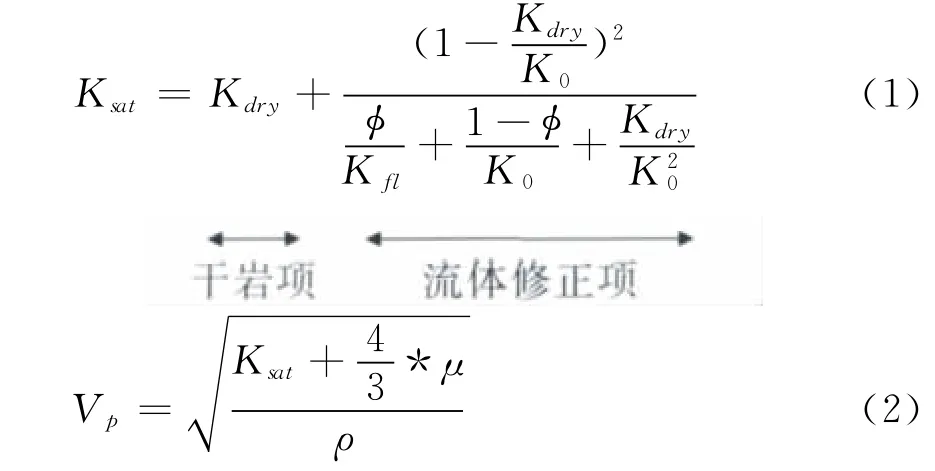
其中 Kdry是干岩石（骨架）有效体积模量；K0是基质矿物（颗粒）体积模量；φ是孔隙度；μ为剪切模量，有μsat＝μdry；Kfl为流体体积模量；Ksat为饱和岩石有效体积模量。

待求量Ksat涉及的参数太多，且获取难度较大。如果没有实验室数据可供使用，也可通过测井资料或经验关系式测量或进行估算［15］。

Gassmann方程的其它常用形式有：

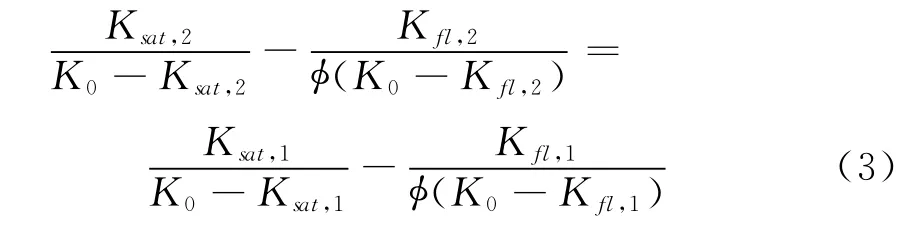
式中 Ksat，1和Ksat，2分别是饱和流体1和饱和流体2岩石的有效体积模量；Kfl，1和Kfl，2分别是饱和流体1和饱和流体2的有效体积模量。

1.2 Gassmann流体替换流程

干岩石替换为有孔隙饱和流体岩石的Gassmann等效替换流程［16］如下：

（1）利用测量干岩样得到的干骨架速度，计算基质矿物体积模量和剪切模量。

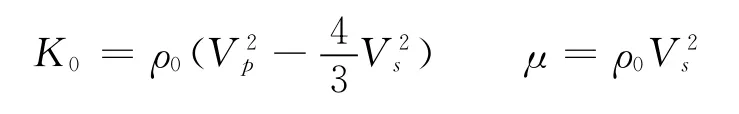
式中 ρ0为基质矿物颗粒平均密度。

（2）利用Biot系数［17］求取干岩石的有效体积模量Kdry。

（3）利用式（1）求取饱和岩石的有效体积模量Ksat。

（4）求取等效密度。

ρ等效＝ （1－φ）＊ρ0＋φ＊ρfl

（5）在剪切模量保持一致条件下，利用式（2）求取等效速度。

一致孔隙度下流体状态1岩石替换成流体状态2岩石的等效替换流程［18］如下：

（1）根据流体1饱和时测得的纵波速度、横波速度和密度，提取饱和岩石体积模量和剪切模量。

（2）用式（3）转换饱和状态2岩石体积模量。

（3）转换密度。

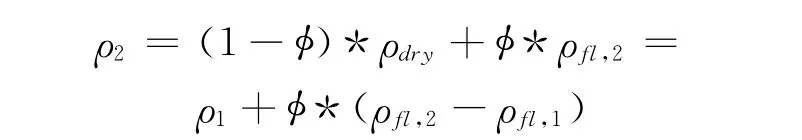
其中 ρ1、ρ2分别是饱和流体岩石1、岩石2的密度；ρfl，1、ρfl，2分别是流体岩石1、岩石2的密度。

（4）剪切模量保持一致。

（5）利用式（2）求取等效速度。

2 岩石速度倒转现象成因分析

图1是作者根据Gregory［13］的测试结果，整理出的不同孔隙度岩石速度变化规律曲线。砂岩孔隙度分为三类，各类曲线饱和度变化速度趋势不一致，但是总的趋势是在中高孔隙度条件下，中部部份含水岩石速度明显低于100%含气岩石速度。同时，不管孔隙度高和低，100%含水岩石速度都是大于100%含气岩石，所以在应用Gassmann方程进行流体替换时，出现的100%含气岩石速度大于含水并不符合岩石物理实验室测试规律，因此开展储层岩样速度倒转现象成因分析是有意义的。同时，利用现有技术进行流体饱和度变化数值模拟，分析碳酸盐岩孔隙度分类界限。

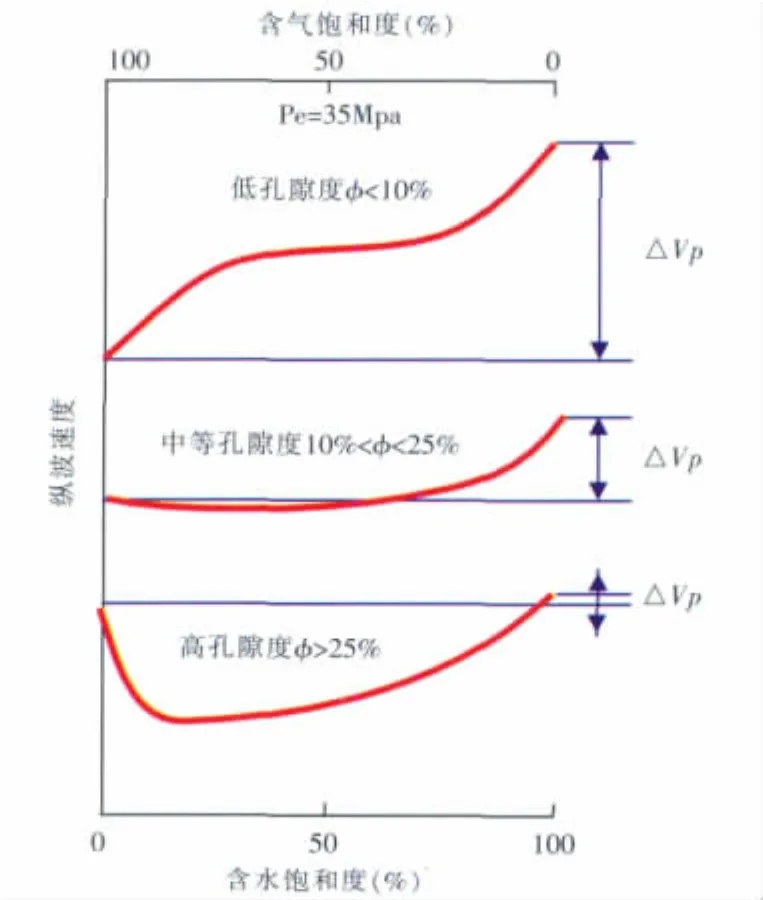
图1 不同孔隙度岩石速度变化规律总结Fig.1 The change discipline summary of different porosity rock velocity

2.1 岩石速度倒转成因分析

设计气～水流体混合模型，见下页表1。根据表1模型及流体参数，灰岩替换结果如下页图2所示。可以看到，当孔隙度大于20%以后，出现了100%含气等效速度大于100%含水情况。从式（1）和式（2）可以看到，饱和岩石体积模量由两项组成，干岩项和流体修正项；纵波速度由三项因素影响，饱和岩石体积模量、剪切模量和密度项。因此从孔隙流体修正项、饱和岩石体积模量、密度项进行分析是有依据的。

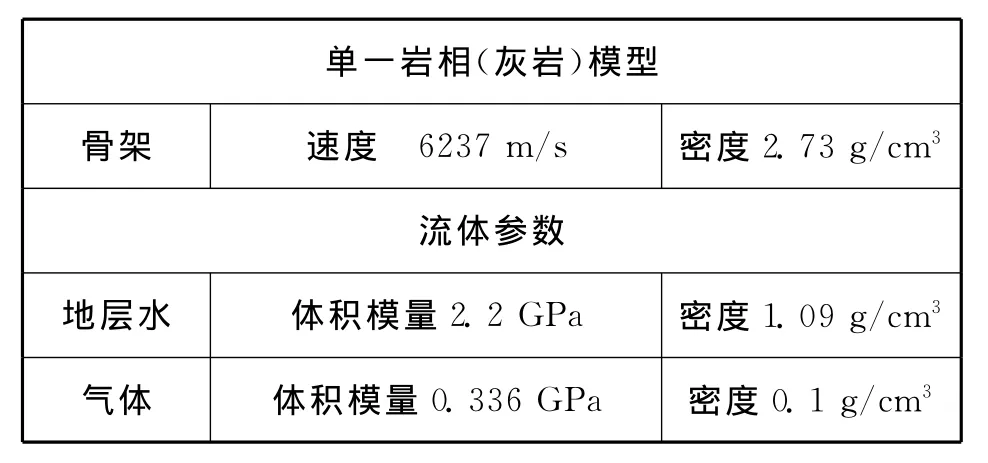
表1 灰岩模型及流体参数表（HCL地区）Tab.1 Limestone model and fluid parameter list（HCL Area）

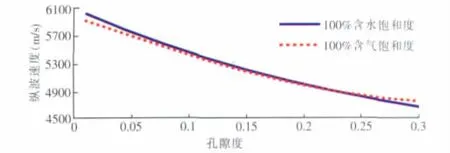
图2 气～水模型速度随孔隙度变化曲线（灰岩岩样）Fig.2 Porosity changes curve with velocity in gas－water model（limestone sample）

图3 为流体修正项随孔隙度变化曲线。由图3可以看出，Gassmann方程计算得到的流体修正项部份，100%含水岩石变化总是大于含气，不是倒转成因。

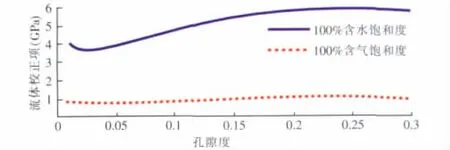
图3 气～水模型流体修正项随孔隙度变化曲线Fig.3 Porosity changes curve with fluid item in gas－water model

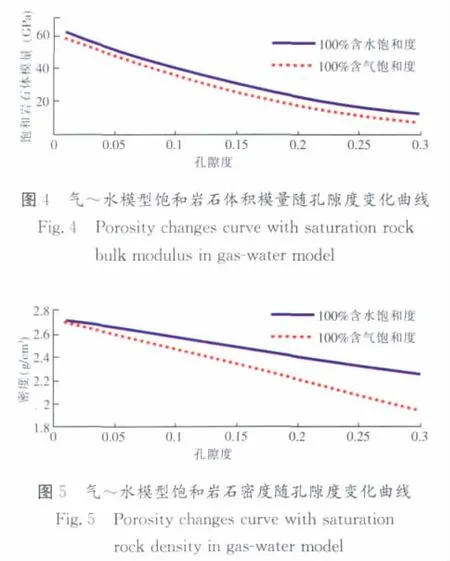
图4 是饱和岩石体积模量随孔隙度变化曲线。由图4可以看到，100%含水岩石体积模量总大于含气，也不是倒转成因。随着孔隙度的增加，二者同时减小，二者差值随孔隙度增加增大。

图5为饱和岩石密度随孔隙度变化曲线。由图5可以看到，随着孔隙度的增加，100%含水和含气岩石的密度在同时减少，但是减小的趋势并不一致。100%含水在孔隙度变化范围内，密度变化为0.6g／cm3。对应的含气岩石变化为0.9g／cm3。从式（2）纵波速度公式解释，在饱和岩石体积模量差异不大，且剪切模量恒定情况下，当密度变化较大时，就会造成100%含气岩石等效速度在一定的孔隙度后比含水大。归根到底是分子的变化率小于分母的变化率，相除后其值增大。

为了验证密度差变化太大，是否为真正倒转现象出现的原因，下页图6给出了气体密度分别为0.05g／cm3和0.5g／cm3时速度随孔隙度的变化曲线。由图6可以看到，密度为0.05g／cm3时出现“倒转现象”的临界孔隙度点向小孔隙度方向移动；而在气体密度为0.05g／cm3时，有效孔隙度范围内不发生倒转。这说明随孔隙度增加，完全饱水和饱气岩石等效密度差异过大是引发Gassmann方程岩石速度倒转现象的成因。

为了说明其它储层岩样同样存在这样的倒转现象，岩石模型数据见下页表2，引入砂泥岩储层岩石进行替换分析说明（见下页图7），可以看到，对于砂泥岩储层气～水模型速度随孔隙度变化曲线，同样存在倒转现象，这都说明是由于对比替换层等效密度差异过大造成的“倒转现象”。

2.2 孔隙度恒定流体饱和度变化数值模拟

岩石物理模型数据见表1。流体替换流程参考1.2节。在孔隙度保持一致情况下，对石灰岩模型中饱含气～水流体时饱和度变化情况进行数值模拟。

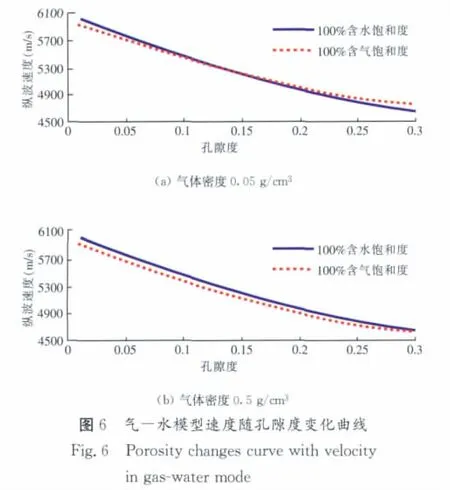
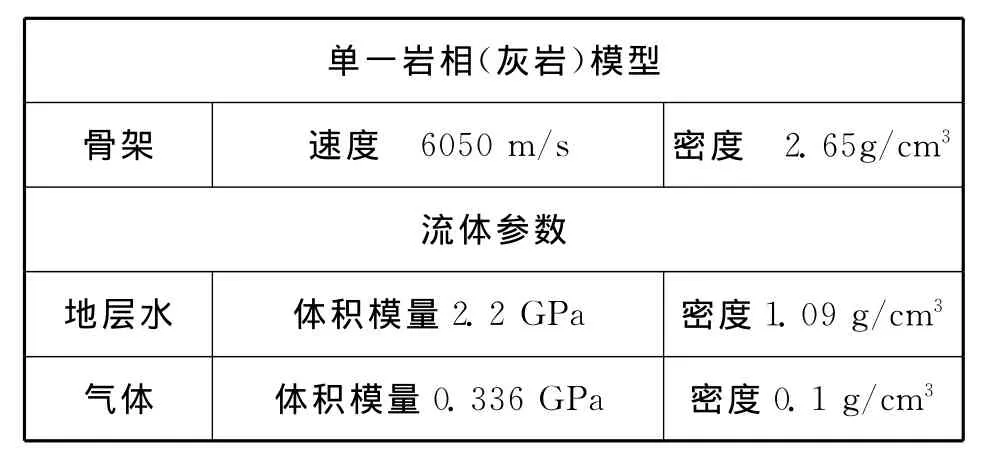
表2 砂岩模型及流体参数表Tab.2 Sandstone model and fluid parameter list

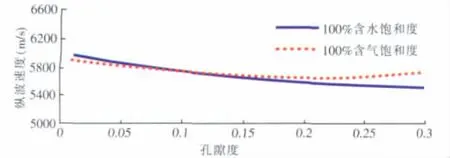
图7 气～水模型速度随孔隙度变化曲线（砂泥岩岩样）Fig.7 Porosity changes curve with velocity in gas－water model（sandstone sample）

从图8饱和度变化曲线可知，利用数值模拟技术对碳酸盐岩岩样饱和度变化模拟结果，同实测饱和度变化数据趋势基本一致，只是对孔隙度的分类区间不同。碳酸盐岩孔隙度分为高孔隙度和低孔隙度，分界线点应该在5%：低于5%的模拟结果同实验室测试的低孔隙度趋势相近；高于5%后中部含水岩石速度明显低于完全含气岩石速度，这与实验室测试分类中的中或高孔隙度趋势是一致的。

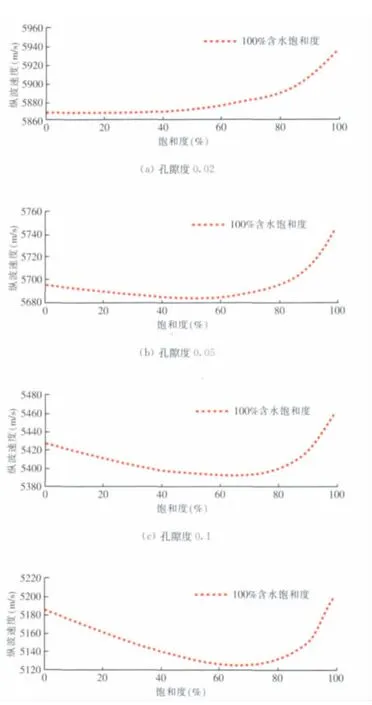
图8 气～水模型速度随含水饱和度变化曲线Fig.8 Water saturation changes curve with velocity in gas－water model

利用表3（见下页）中模型及流体参数，对白云岩岩样进行饱和度变化模拟。从下页图9模拟结果可以看到，在三相基质矿物颗粒组成的背景介质中，模拟结果同样是中部含水岩石速度明显低于完全饱气岩石速度，与实验室测试的高孔隙度曲线一致。

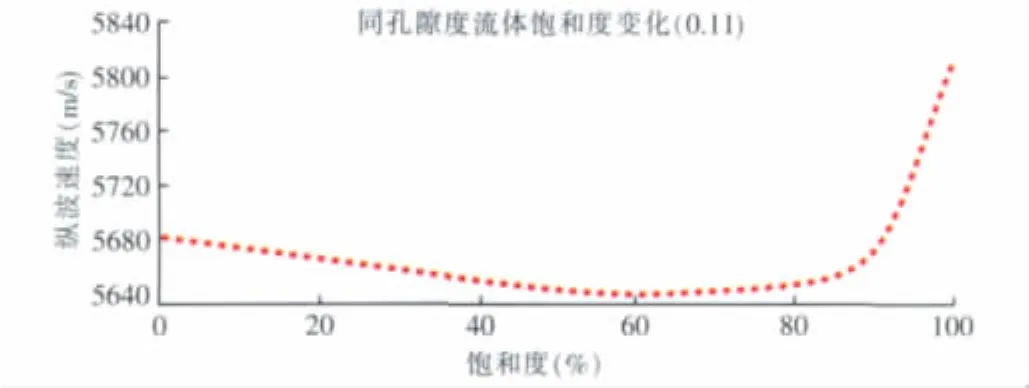
图9 气～水模型速度随饱和度变化曲线Fig.9 Water saturation changes curve with velocity in gas－water model

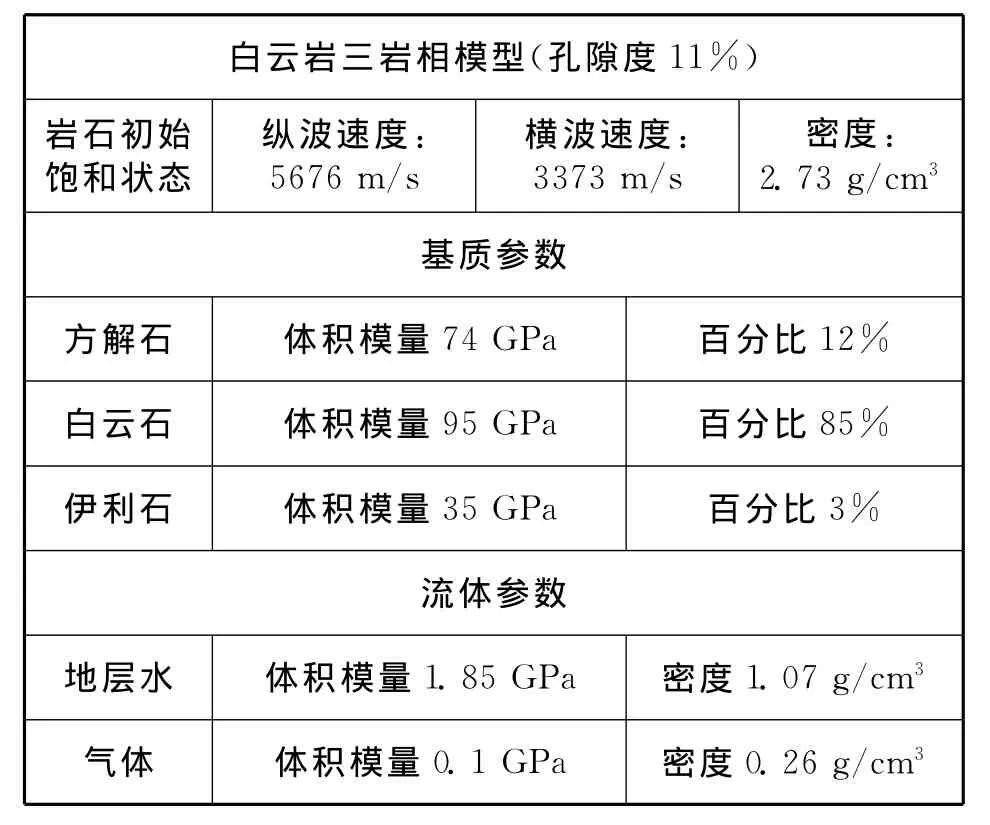
表3 白云岩模型及流体参数表Tab.3 Dolomite model and fluid parameter list

3 结束语

以实验室测试岩样数据为标准，作者通过数值模拟技术对Gassmann方程岩石速度倒转现象进行了成因分析，发现是由于对比替换层等效密度差异过大造成的“倒转现象”。同时，作者还对碳酸盐岩的岩样进行饱和度变化数值模拟，模拟结果同实验室测试趋势一致，只是碳酸盐岩的岩样对孔隙度分类的界限不同。因此在实际资料流体替换过程中，应该重点考虑密度参数。同时，作者在文中还强调了流体替换正演的重要性，在一定物理意义下的流体替换才有实际价值。

［1］ 王炳章.地震岩石物理学及其应用研究［D］.成都：成都理工大学，2008.

［2］ MAVKO.岩石物理手册－孔隙介质中的地震分析工具［M］.北京：中国科学技术大学出版社，2008.

［3］ GASSMANN F.Elastic waves through a Packing of spheres［J］.GeoPhysics，1951，16（3）：673.

［4］ WHITE J.E.Computed seismic speed and attenuation in rocks with partial gas saturation［J］.GeoPhysics，1965，40（2）：224.

［5］ GREENBERY M.L.，Castagna J.P.Shear－Wave Velocity Estimation in Porous Rocks：Theoretical Formulation，Preliminary Verification and Applications［J］.Geophysical Prospecting，1992（40）：195.

［6］ 伍向阳，方华，陈祖安.储层砂岩声波速度预测［J］.地球物理学进展，1993，14（1）：56.

［7］ 云美厚，管志宁.储层条件下砂岩纵波和横波速度的理论计算［J］.石油物探，2002，41（3）：289.

［8］ 王玉梅，苗永康，孟宪军，等.岩石物理横波速度曲线计算技术［J］.油气地质与采收率，2006，13（4）：58.

［9］ 黄伟传，杨长春，范桃园，等.岩石物理分析技术在储层预测的应用［J］.地球物理学进展，2007，22（6）：1791.

［10］李凌高，王兆宏，甘利灯，等.基于叠前地震反演参数的流体饱和度定量预测方法［J］.石油物探，2009，48（2）：121.

［11］李燕，刘浩杰，王玉梅.Gassmann模型机理分析及其应用［J］.勘探地球物理学进展，2010，33（1）：16.

［12］马淑芳，韩大匡，甘利灯，等.地震岩石物理模型综述［J］.地球物理学进展，2010，25（2）：460.

［13］GREGORY，A.R.Fluid saturation effects on dynamic elastic properties of sedimentary rock［J］.Geophysics，1976，41（5）：895.

［14］王之敬.地震岩石物理学基本准则［J］.石油物探译丛，2001，4（1）：1.

［15］林凯.基于Gassmann方程的弹性参数数值模拟研究［D］.成都：成都理工大学，2010.

［16］林凯，贺振华，熊晓军，等.基于Gassmann方程的鲕滩储层流体替换模拟技术及其应用［J］.石油物探，2009，48（5）：494.

［17］HILTERMANF J.地震振幅解释［M］.孙夕平，赵良武，译.北京：石油工业出版社，2006.

［18］林凯，贺振华，熊晓军，等.基于Gassmann方程的流体替换流程［J］，长江大学学报：自然科学版，2009，6（1）：180.