水泥砂浆锚杆中的导波传播机理研究
何文,高忠,赵奎
(江西理工大学,a.工程研究院;b.资源与环境工程学院,江西赣州341000)
水泥砂浆锚杆中的导波传播机理研究
何文a,高忠b,赵奎a
(江西理工大学,a.工程研究院;b.资源与环境工程学院,江西赣州341000)
对纵向导波在水泥砂浆锚固锚杆中的传播特性进行了分析.根据弹性动力学理论,首先建立了三维柱坐标的水泥砂浆锚固锚杆中纵向导波的频散方程,并数值求解了纵向导波的相速度、能量速度和衰减频散曲线,由频散曲线可知,500 kHz范围内水泥砂浆锚固锚杆中存在5个纵向导波模态;然后分析了特定频率下,纵向导波在水泥砂浆锚固锚杆横截面的位移分布,结果表明:锚杆截面上轴向位移越大,代表纵向导波对锚杆体的周向缺陷越敏感,而锚杆与水泥砂浆接触面上的径向位移越大,则表示从锚杆泄漏至水泥砂浆中的纵向导波能量越大;最后讨论了锚杆尺寸和水泥砂浆材料属性的变化对纵向导波的能量速度和衰减频散曲线的影响.为实现水泥砂浆锚杆锚固质量纵向导波的无损检测提供了理论基础.
纵向导波;锚固锚杆;传播机理;无损检测
0 引言
水泥砂浆全长锚固锚杆是目前岩土锚杆支护工程中的一种主要支护形式,它主要用于加强边坡和深基坑等岩土工程的稳定性.以往,有关岩土中锚杆(索)的研究重点在于岩土中锚杆(索)的应力分布及对周围岩层变形的影响[1].近年来,国内外的研究学者及工程人员尝试将无损检测技术应用于检测锚杆的锚固质量,例如应力波反射法[2-3]、电磁法[4]、声发射检测法[5]等,并取得了一定的检测成果.导波技术是近年来兴起的一种新的无损检测技术,它具有检测距离远、成本低、操作简便等特点[6].现已经有研究学者逐步开展了有关锚固锚杆结构中导波的传播特性的研究,例如何存富等人[7]实验研究了低频纵向导波在埋于地基的锚杆中的传播特性.张昌锁[8]分别利用实验和数值模拟的方法研究了不同龄期的水泥砂浆对锚固锚杆中低频纵向导波的传播速度和衰减的影响.王成等人[9]通过理论分析和数值模拟,研究了高、低频超声导波在树脂锚固锚杆中传播的特性.张世平[10]提出了高频导波检测注浆锚杆完整性的一种方法.Zou[11]研究了水泥砂浆与锚杆间脱层对锚杆中导波传播的影响.He[12]通过实验的方法优化了高频导波检测锚杆体缺陷的激发波频率.
文中从理论方面分析水泥砂浆锚固锚杆中纵向导波的传播机理.对水泥砂浆锚固锚杆中纵向导波频散曲线及特定频率导波的波结构进行分析,并对因锚杆尺寸及水泥砂浆层材料属性的变化引起的导波频散曲线的变化规律进行探讨,为将导波技术有效地应用于锚杆锚固质量的检测奠定理论基础.
1 频散方程的建立
水泥砂浆锚固锚杆结构的简化模型如图1所示.图中的内层介质为锚杆,外围介质为水泥砂浆.文中,r1为锚杆的半径,水泥砂浆为径向尺寸无限大的介质,并假设导波沿z轴传播.为了便于分析,此处的锚杆设为自由圆钢锚杆.
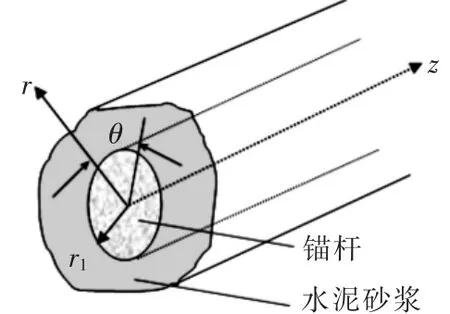
图1 水泥砂浆锚固锚杆结构的简化模型
当波在锚杆和水泥砂浆层中传播时,均满足式(1)
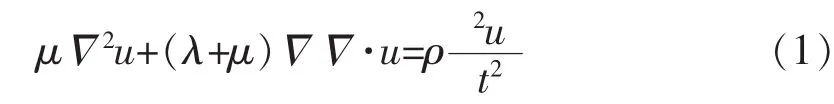
利用位移的海姆霍茨(Helmholtz)分解


假设纵向导波以简谐波的形式在水泥砂浆锚固锚杆中沿z轴传播,对于圆钢锚杆
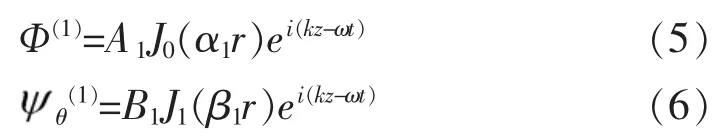
式中:A1和B1分别为向外传播的纵波和横波的幅值,且均为待定常波的圆频率,k为波数,cp1和cs1分别为圆钢锚杆的纵波和横波波速.J0(x)和J1(x)分别为零阶和一阶的第一类Bessel函数.考虑到第二类贝塞尔函数在原点的奇异性,式(5)和式(6)中分别省略了Y0(αr)和Y1(βr)项.
将式(5)和式(6)代入式(3)和式(4),得出纵向导波在圆钢锚杆中的径向和轴向位移的表达式为
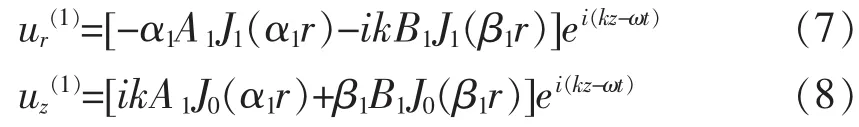
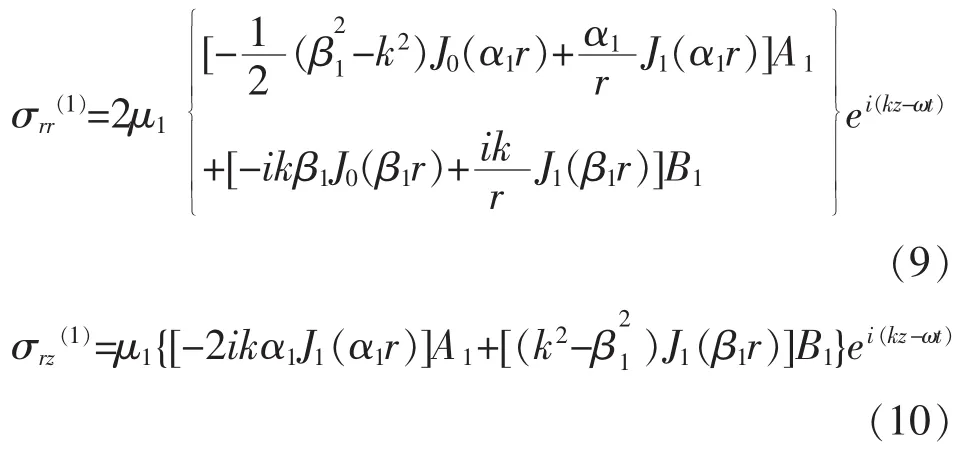
对于水泥砂浆层
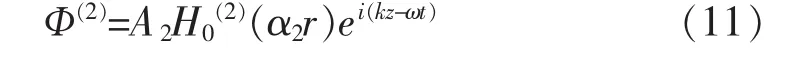
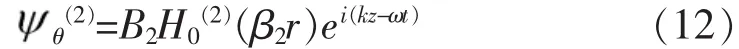
式中:A2和B2分别为向外传播的纵波和横波的幅值,且均为待定常波的圆频率,k为波数,cp2和cs2分别为水泥砂浆层中的纵波和横波波速.考虑到波在水泥砂浆层中传播时,波将在无穷远处衰减,并不能反射回锚杆处,所以引入第二类Hankel函分别为零阶和一阶的第二类Hankel函数.

问题的边界条件为:
在r=r1的表面上,即锚杆与水泥砂浆的接触面上,

将式(7)~式(10)、式(13)~式(16)代入边界条件式(17)中,产生一组特征方程,方程的矩阵形式为

其中N=[A1B1C1D1]T,[Mij]为4×4的系数矩阵,为使式(18)有非零解,其系数行列式必须为零,即:

式(19)即为水泥砂浆锚固锚杆中纵向导波的频散方程,式中系数具体如下.
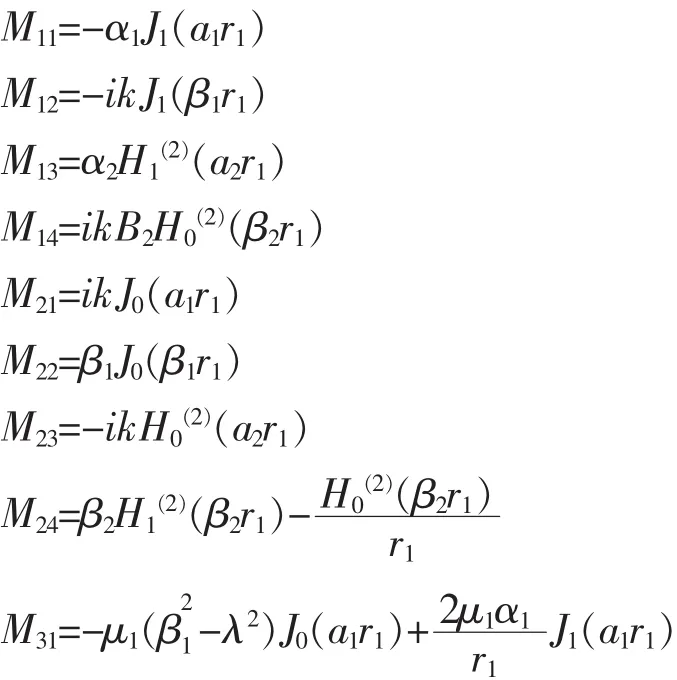

导波在水泥砂浆锚固锚杆中传播时,部分导波能量将从锚杆体泄漏至水泥砂浆层中引起导波的衰减.为了表征导波的衰减情况,将波数k表示为[13]

式中,cph为导波的相速度,其表达式导波的衰减值.
2 频散曲线的计算
理论计算中使用的水泥砂浆锚固锚杆的材料属性见表1.圆钢锚杆的直径为Ф22 mm.
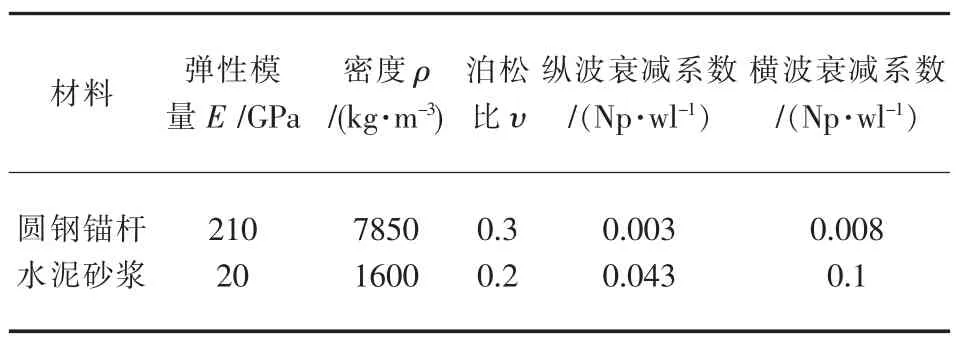
表1 水泥砂浆锚固锚杆的材料属性
求解频散方程得到的水泥砂浆锚固锚杆中纵向导波的相速度频散曲线如图2所示.由图2可知,500 kHz频率范围内,水泥砂浆锚固锚杆中存在五个纵向导波模态,并且每个模态的相速度随着频率的变化而不同,说明这些模态的导波是频散的;与自由圆钢锚杆中纵向导波的频散曲线不同,图2中的L(0,1)模态存在截止频率,其值约为10 kHz.
导波在水泥砂浆锚固锚杆中传播时,引起导波能量衰减的原因有两种:锚杆体材质引起的导波衰减和导波能量泄漏到水泥砂浆中.这两种衰减均能够用α表示.而此时导波的传播速度为能量速度,而非群速度.用群速度代表导波的传播速度误差较大.水泥砂浆锚固锚杆中纵向导波的能量速度频散曲线见图3.由图3可知,500 kHz范围内,L(0,1)模态的最大和最小能量速度值分别出现在41 kHz和153 kHz;而频率为231 kHz时,L(0,2)模态的能量速度达到最大值.

图2 水泥砂浆锚固锚杆中纵向导波的相速度频散曲线
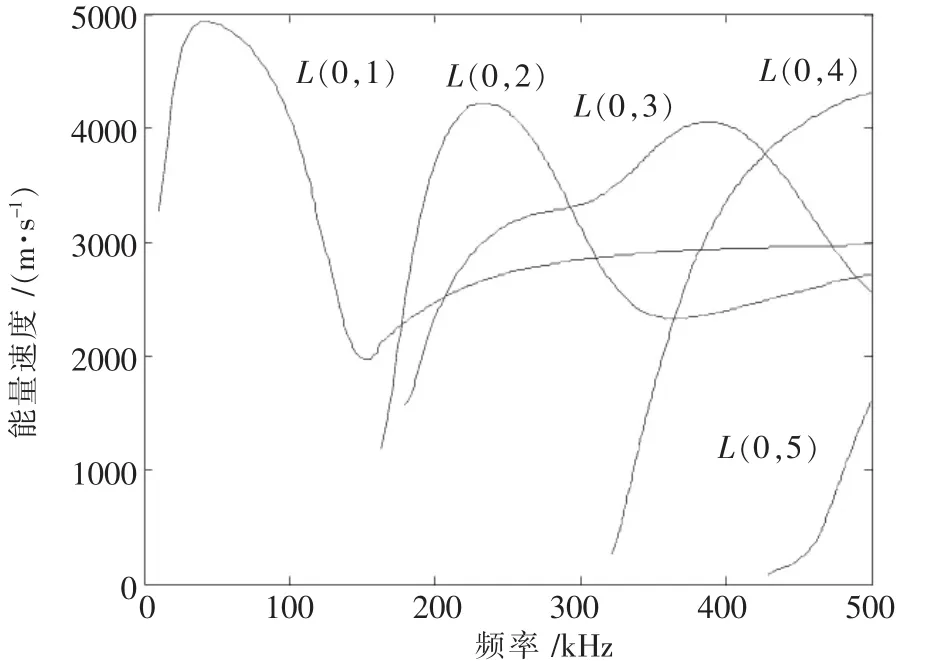
图3 水泥砂浆锚固锚杆中纵向导波的能量速度频散曲线
水泥砂浆锚固锚杆中纵向导波的衰减频散曲线见图4.从图4可以看出,L(0,1)模态的衰减值随着频率的增大先减小,然后再增大,频率为158 kHz时,L(0,1)模态的衰减值达到最大值,而158 kHz以后,衰减值又减小.L(0,2)模态衰减值随频率增大的总体趋势是减小的.

图4 水泥砂浆锚固锚杆中纵向导波的衰减频散曲线
3 波结构分析
多层柱状复合结构中,纵向导波的轴向位移分量对于检测周向缺陷的灵敏度起决定作用,而导波在锚杆外表面上的径向位移对波在传播过程中能量的泄漏起决定作用[14].
41 kHz和153 kHz的L(0,1)模态导波在水泥砂浆锚固锚杆横截面上的位移分布分别见图5和图6.
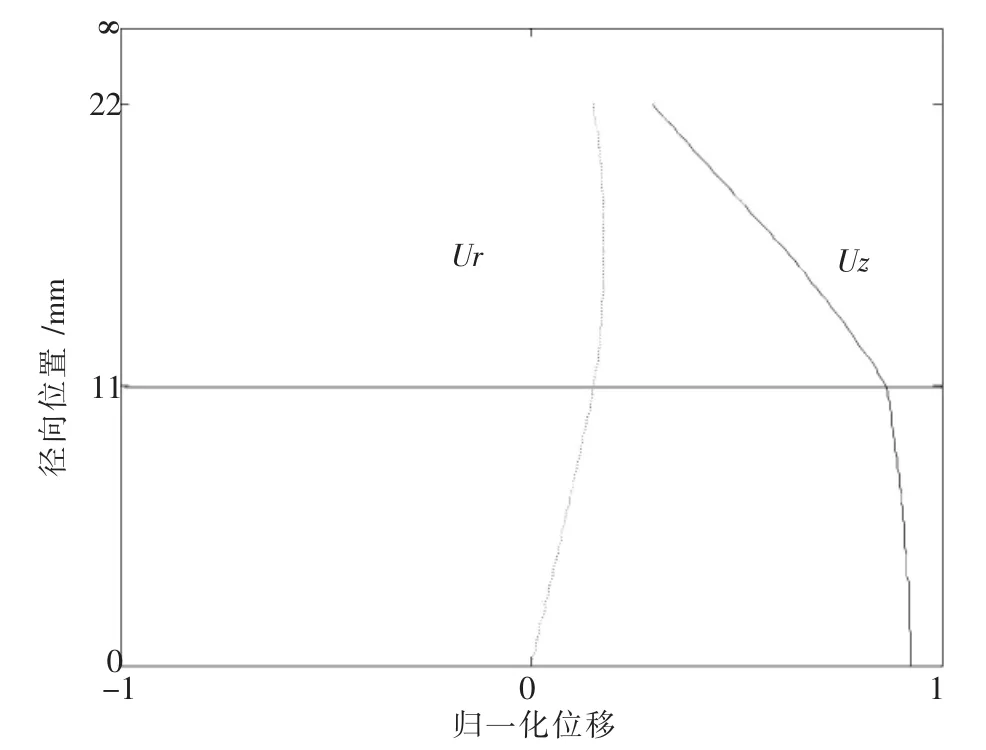
图5 水泥砂浆锚固锚杆中41 kHz的L(0,1)模态的波结构
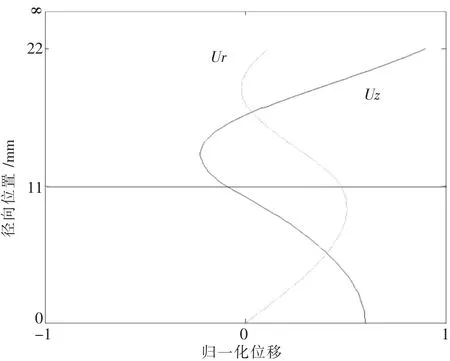
图6 水泥砂浆锚固锚杆中153 kHz的L(0,1)模态的波结构
从图5可以看出,在锚杆与水泥砂浆的接触面及水泥砂浆层中,径向位移值都比较小,代表导波的能量泄漏较小;锚杆截面上的轴向位移分布均匀且值较大,代表41 kHz纵向导波对锚杆体上缺陷检测灵敏度高.135 kHz导波(图6)的径向位移值在锚杆与水泥砂浆的接触面上较大,代表更多的导波能量从锚杆泄漏至水泥砂浆层中;随着径向位置的增大,锚杆体中的轴向位移逐渐减小,表示该频率导波对靠近锚杆中心的缺陷检测较为灵敏.
231 kHz的L(0,2)模态导波在水泥砂浆锚固锚杆横截面上的位移分布如图7所示.由图7可知,导波在锚杆与水泥砂浆接触面的径向位移较小,代表从锚杆泄漏至水泥砂浆层中能量较少;锚杆体中的轴向位移随着径向位置的增大而减小.

图7 水泥砂浆锚固锚杆中231 kHz的L(0,2)模态的波结构
4 参数变化对频散曲线的影响
4.1 圆钢锚杆直径的变化
圆钢锚杆直径的变化对水泥砂浆锚固锚杆中的L(0,1)模态频散曲线的影响见图8.由图8(a)可知,在0~144 kHz范围内,L(0,1)模态的能量速度随着锚杆直径的增大而减小;而在166~500 kHz范围内,能量速度随着锚杆直径的增大而增大;随着频率的增大,三种锚杆直径的L(0,1)模态的能量速度趋于一致.
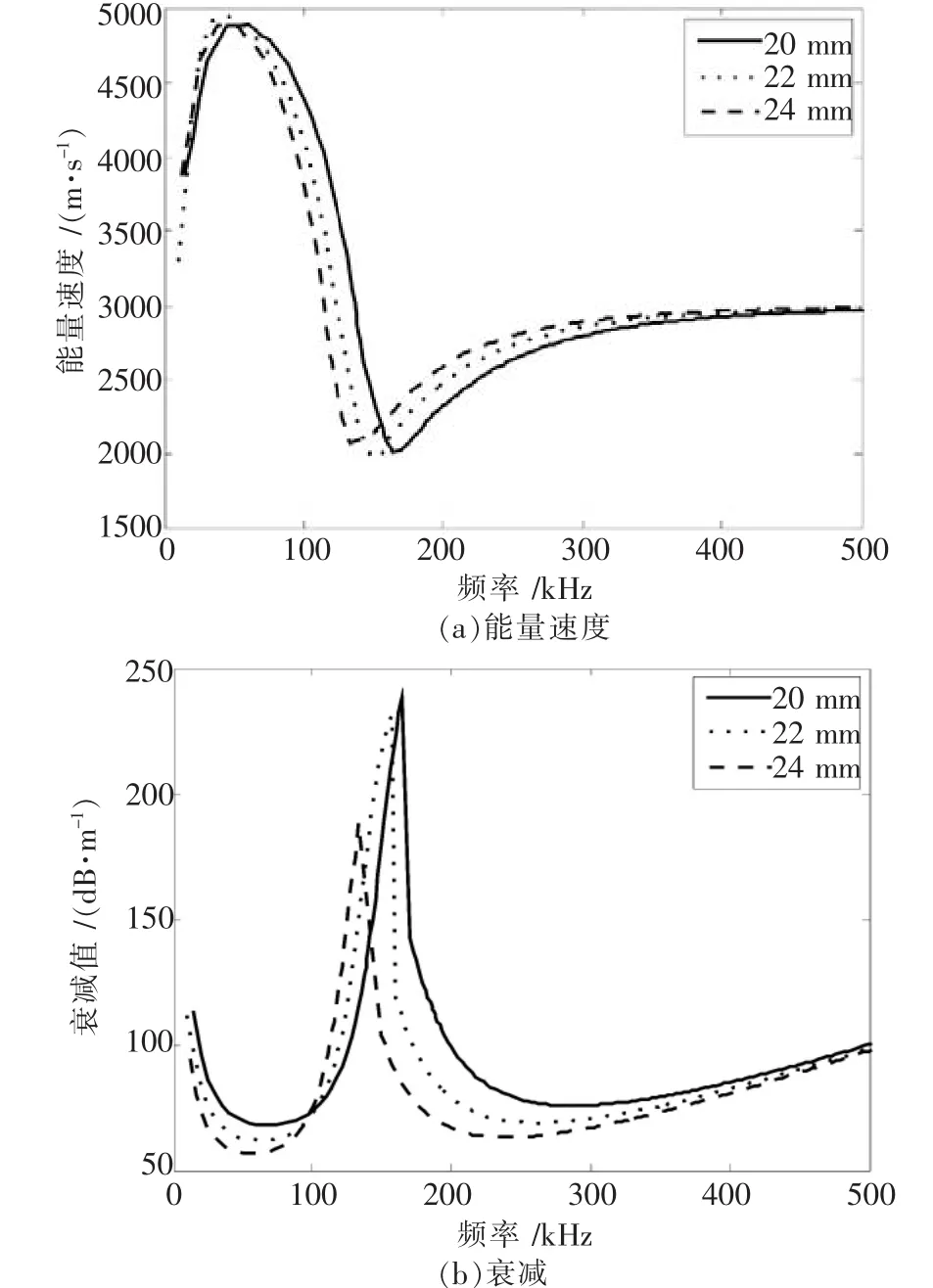
图8 圆钢锚杆直径的变化对L(0,1)模态频散曲线的影响
由图8(b)可知,随着锚杆直径的增大,L(0,1)模态的衰减频散曲线向左下方移动.
4.2 水泥砂浆弹性模量的变化
水泥砂浆弹性模量的变化对水泥砂浆锚固锚杆中的L(0,1)模态频散曲线的影响如图9所示.从图9(a)可以看出,80 kHz范围内,水泥砂浆弹性模量越大,L(0,1)模态的能量速度越小,而频率大于153 kHz时,L(0,1)模态的能量速度随着水泥砂浆弹性模量的增大而增大,但差距不大.
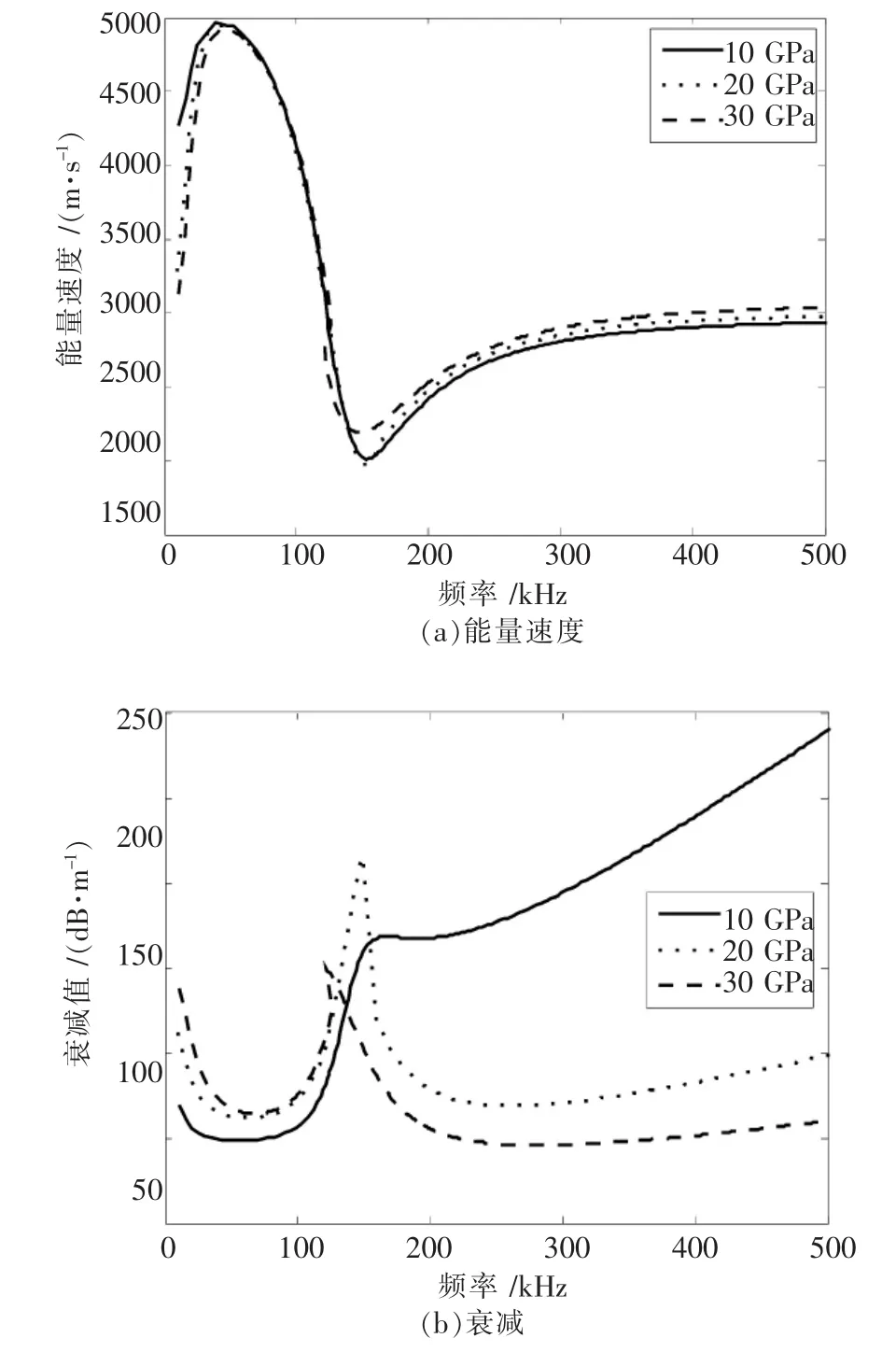
图9 水泥砂浆弹性模量的变化对L(0,1)模态频散曲线的影响
由图9(b)可知,120 kHz范围内,水泥砂浆弹性模量的弹性模量越大,L(0,1)模态的衰减值越大;而频率大于180 kHzH以后,情况正好相反.
5 结论
文中从理论的角度分析了纵向导波在水泥砂浆锚固锚杆中的传播特性.500 kHz范围内,水泥砂浆锚固锚杆中存在5个纵向导波模态,且均有频散性.纵向导波模态的最大能量速度对应频率的导波在水泥砂浆锚固锚杆中的位移分布主要在锚杆体内,所以此频率导波适用于检测锚杆体的周向缺陷;纵向导波模态的最小能量速度对应频率的导波在水泥砂浆锚固锚杆中的位移分布主要分布在锚杆和水泥砂浆的接触面上,所以此频率导波在锚杆中的衰减较大,不适合于锚杆体缺陷的检测,但可以对锚杆和水泥砂浆接触面上的缺陷进行检测.
[1]王贵虎,唐述敏.三软综放沿空锚网索支护巷道回采期间围岩变形特征[J].江西理工大学学报,2007,28(4):17-21.
[2]汪明武,王鹤龄.锚固质量的无损检测技术[J].岩石力学与工程学报,2002,21(1):126-129.
[3]李义,王成.应力反射波法检测锚杆锚固质量的实验研究[J].煤炭学报,2000,25(2):160-164.
[4]陈波,鲁永康,郭玉,等.电磁法检测锚固质量初探[J].工程地球物理学报,2004,1(4):336-339.
[5]郭安萍.声发射技术在锚固质量检测中的试验研究[J].中国地质灾害与防治学报,1997,8(2):72-76.
[6]Rose J L.Ultrasonic guided waves in structural health monitoring[J].Key Engineering Materials,2004,270-273:14-21.
[7]何存富,孙雅欣,吴斌,等.超声导波技术在埋地锚杆检测中的应用研究[J].岩土工程学报,2006,28(9):1144-1147.
[8]张昌锁,李义,赵阳升,等.锚杆锚固质量无损检测中的激发波研究[J].岩石力学与工程学报,2006,25(6):1240-1245.
[9]Wang C,He W,Ning J G,et al.Propagation properties of guided wave in the anchorage structure of rock bolts[J].Journal of Applied Geophysics,2009,69(3-4):131-139.
[10]张世平,张昌锁,白世龙,等.注浆锚杆完整性检测方法研究[J].岩土力学,2011,32(11):3368-3372.
[11]Cui Y,Zou D H.Assessing the effects of insufficient rebar and missing grout in grouted rock bolts using guided ultrasonic waves[J].Journal of Applied Geophysics,2012,79:64-70.
[12]He W,Luo X J,Zhao K,et al.Experimental study of high frequency guided wave inspection of anchored bolts[J].Applied Mechanics and Materials,2012,117-119:962-966.
[13]Rose J L.固体中的超声波[M].何存富,吴斌,王秀彦,译.北京:科学出版社,2004.
[14]他得安,刘振清,贺鹏飞.复合管状结构中超声导波的位移分布[J].复合材料学报,2003,20(6):130-136.
Research on the properties of guided wave propagation in cement anchored bolts
HE Wena,GAO Zhongb,ZHAO Kuia
(a.Engineering Research Institute;b.School of Resource and Environmental Engineering Jiangxi University of Science and Technology,Ganzhou 341000,China)
The propagation properties of longitudinal guided wave in cement mortar anchored bolts are studied in this article.Based on the elastodynamic theory,the longitudinal guided wave dispersion equations are established in three dimensional cylindrical coordinate,and the corresponding phase velocity,energy velocity and attenuation dispersion curves are obtained.It can be observed from the dispersion curves that five longitudinal guided wave modes exist in the bolt under the frequency 500 kHz.The displacement distribution of guided wave with certain frequencies is analysed.Results show that guided waves with large axial displacement distribution are sensititive to circumference defects on the bolt while guided waves with large radial displacement distribution in the bolt/cement mortar interface cause great energy leakage;Finally,the effects of bolt size and properties of cement mortar on longitudinal guided wave energy velocity and attenuation dispersion curves are discussed.And the theoretical basis for nondestructive testing of cement mortar anchored bolts using longitudinal guided waves is stated in the article.
longitudinal guided wave;cement anchored bolt;propagation properties;nondestructive evaluation
P631.5;TU45
A
2012-05-08
国家自然科学基金资助项目(51044008);江西省教育厅青年科学基金资助项目(GJJ12365);江西理工大学校级科研基金项目(jxxj11121)
何文(1981-),男,博士,讲师,主要从事岩土工程测试技术和岩体稳定性分析等方面的研究,E-mail:herman3@163.com.
2095-3046(2012)03-0021-05

