基于随机有限断层法的地震烈度计算研究*

王 俊，霍祝青，詹小艳，宋 浩，江昊琳，徐 戈

(江苏省地震局，江苏南京210014)

基于随机有限断层法的地震烈度计算研究*

王 俊，霍祝青，詹小艳，宋 浩，江昊琳，徐 戈

(江苏省地震局，江苏南京210014)

采用基于动力学拐角频率的随机有限断层法，首先模拟计算了东台、如皋及大丰3个台站记录的2006年江苏东台3.8级地震的地震动，并与其实际记录进行比较研究，验证了该方法的计算结果能够较好地反映出江苏地区主震剪切波的主要特征。随后运用该方法模拟计算了1979年江苏溧阳6.0级地震震源区内156个虚拟观测点的地震动，并通过内插值的方式得到此次地震的加速度场分布情况;随后依据峰值加速度统计方法和模糊评定方法，分别计算此次地震的理论烈度分布，结果显示:两种烈度划分方法的结果与实际调查的烈度分布都基本一致，但模糊评定方法的划分结果更加接近真实的烈度分布。

动力学拐角频率;随机有限断层法;合成地震动;地震烈度;溧阳6.0级地震

0 引言

地震烈度是用来描述地震对地面的影响和破坏程度的参数。破坏性地震发生后，除震源的基本参数外，政府和社会公众最迫切想了解的是极震区的震害分布情况，从而为紧急救援争取时间。目前在我国获取震害分布情况的主要途径仍是震后实际的震害考察和评估 (崔建文等，2008)，最短时间也需要数天，不利于救援工作的开展。据统计，在一次地震中，90%以上的建 (构)筑物的破坏是由地震动造成的 (王海云，谢礼立，2009)。地震动是由震源破裂、波在地壳介质中的传播以及场地反应等共同形成的复杂地面运动，在低频段具有确定性而在高频段则表现出强烈的随机性的特征 (Somerville et al，1991;Beresnev，Atkinson，1997)。

对合成地震动的研究，特别是对近场强地震动的研究一直是地震学和地震工程学领域的热点问题。目前国内外已经发展了多种模拟方法，如Aki和Richaids(1986)提出的将地震动表示为震源时间函数和格林函数卷积的方法，可用于长周期地震动的合成;高斯带限白噪声的随机点源方法 (Hanks，McGuire，1981;Boore，1983) 和经验格林函数方法 (Hartzell，1978;Irikura，1983)，可用于高频地震动的合成。其中经验格林函数方法是最为有效的，主要思路是将研究区域内与主震震源机制相似的、信噪比较高的小震记录作为子源响应，从而建立起合成地震动的经验格林函数。该方法的优点是在地震动的模拟过程中不需要再计算地震波的传播路径效应和场地响应，因为小震记录中已包含了这些信息，但不足之处是无法在地震记录稀疏或缺乏余震记录的地区使用。

随机有限断层震源模型方法解决了经验格林函数方法中对余震记录要求较高这一问题 (Beresnev，Atkinson，1997，1998)。对于远源和小震，采用随机点源模型来模拟;对于近源或强震，将主震的破裂过程视为破裂面上一系列子源破裂的结果 (Beresnev，Atkinson，2002)，并用随机方法产生满足Brune震源模型的子源 (Brune，1970)，最后通过叠加各子源的地震动合成具有主震破裂特征的地震动。该方法已被应用于国内外许多地区的地震动参数估计中，在多次大震地震动的模拟中显示出良好的效果 (Atkinson，Beresenev，2002;Zafeiria，Beresnev，2003;石玉成等，2005;崔建文等，2008)。但该方法基于静力学拐角频率，合成地震动会随着子断层的尺寸变化发生显著的变化，Motazedian和Atkinson(2005)引入了动力学拐角频率将其进一步改进，从而弥补了原方法中的缺陷。

场点的地震动与地震烈度之间是怎样的一种关系?如何依据地震动快速地评定出震区的烈度分布，是震后紧急救援更加关注的实际问题。目前，地震烈度的计算方法主要归纳为统计回归法和模糊评定法 (袁一凡，1998;李山有等，2002)。统计回归法是通过统计回归的方法，仅考虑10 Hz左右的地震动峰值加速度与地震烈度之间的函数关系。袁一凡 (1998)考虑到宏观烈度定义的模糊性，引入模糊评定方法来建立地震动参数与地震烈度之间的关系，该方法可以将更多的地震动参数纳入评定系统中，能够更好地反映出两者的内在关系。

目前，江苏省虽然已形成了布局较为合理的微震、强震动观测网络，但仍然没有正式开展地震烈度速报的相关工作。1979年江苏溧阳发生M6.0地震，造成了巨大的经济损失和人员伤亡，震后专家学者进行了大量的科学考察和震害评估，绘制了震区真实烈度分布图 (胡连英等，1997)。为了在将来破坏性地震发生后，实现快速划分地震烈度，笔者以溧阳地震为例，首先采用基于动力学拐角频率的随机有限断层法，合成研究区内一定数量的虚拟场点的地震动;然后根据峰值加速度统计法和模糊评定方法计算虚拟场点的理论烈度分布，并与真实烈度分布进行对比研究，以判断基于合成地震动的地震烈度计算的有效性。

1 基于动力学拐角频率的随机有限断层法

Beresnev和Atkinson(1997，1998)将地震断层面视为由若干个大小相等的矩形子断层所构成的，每个子断层即为一个点源 (或子源)，如图1所示。地震的破裂过程是从破裂起始点以一定的破裂速度 (一般为剪切波速的0.8倍)向外呈辐射状传播，当传播到每个子源的中心时，该子源即被触发，且子源的震源谱符合 Brune模型(Brune，1970)。因此，某一时刻所有子源在某一基岩观测点上由剪切波引起的地震动，可在时域中经过相位校正后进行叠加而求得，表示为

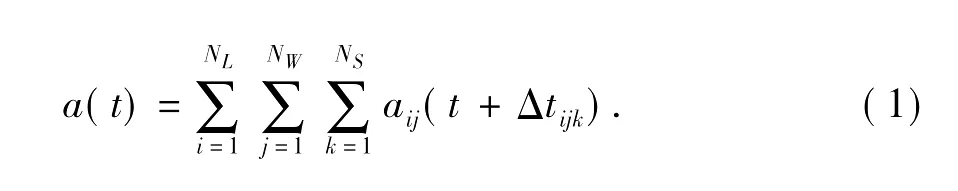
式中，NL、NW分别为沿着断层走向和下倾方向的子断层数;NS为子源被触发的次数;Δtijk为地震波从破裂起始点传播至第ij个子源的时间延迟与该子源至观测点的传播时间延迟之和;aij(t)为第ij个子源在观测点由剪切波引起的地震动。

图1 随机有限断层法的几何示意图Fig.1 Geometric schematic diagram of stochastic finite faults method

Beresnev和Atkinson(1997，1998)在合成地震动时，使用的是基于Brune模型 (Brune，1970)的静力学拐角频率，其对子断层的大小有严格的限制，为了保证地震矩的能量守恒，要求一个子源被多次触发。在合成大地震的地震动时要求子断层的尺寸在5～15 km范围内，限制了对小震地震动的模拟，并且难以模拟出大震的长周期成分(Motazedian，Atkinson，2005)。为了弥补使用静力学拐角频率合成方法的缺陷，Motazedian和Atkinson(2005)引入了动力学拐角频率，其优点是通过给各个子源赋予不同的拐角频率，来表示破裂面上地震波频率的非均匀性，同时达到拐角频率随破裂面积的增大而下降的趋势。将第ij个子源的震源加速度谱定义改写为

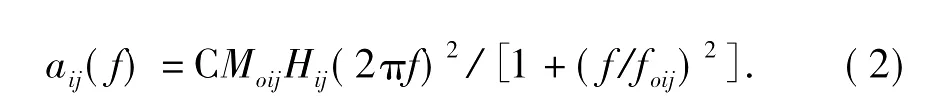
式中，C是标量常数 (Boore，1983);Hij=1/{exp(－πfk)exp(－πfRij/Qβ)/Rij}，是保证子源高频辐射守恒的标度因子;其中，Q是介质的弹性衰减系数;β是剪切波速;Rij是体波的几何衰减模型;foij是子源的拐角频率，可以表示为在t时刻时子断层破裂总数NR(t)的函数:

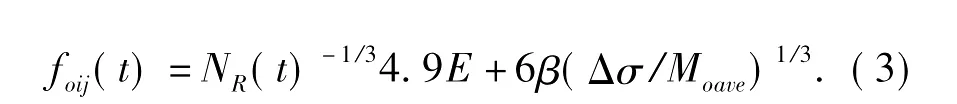
式中，E为整个断层在高频段的总辐射能;Moave=M0/N，为子断层的平均地震矩。

2 地震动的合成

为了检验基于动力学拐角频率的随机有限断层法，笔者首先以2006年12月26日江苏东台MW3.8地震为实例进行模拟。该次地震后分布在不同方位的东台、如皋及大丰3个强震台清晰地记录到此次地震，震中距分别为22.4 km、36.4 km、53.3 km，其震中位置及震源机制分布如图2所示。

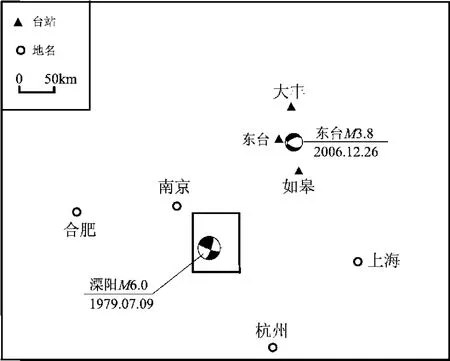
图2 溧阳M6.0地震、东台MW3.8地震的震中位置及震源机制Fig.2 Epicenter locations and focal mechanisms of Liyang M6.0 and Dongtai MW3.8 earthquakes

孙业君 (2010)①孙业君.2010.2006年东台地震M3.8地震破裂参数研究.利用P波初动反演得到了江苏东台MW3.8地震的震源机制解，并且根据地震多普勒效应计算了震源的破裂参数 (表1)。随机有限断层法的全局基本参数参照Motazedian和Atkinson(2005)的研究结果 (表2)。地壳初始模型参考黄耘等 (2006)根据人工地震探测的研究结果，在10～15 km深度范围内江苏地区的剪切波速约3.5 km/s;(2)式中标度因子里的弹性衰减系数Q值采用詹小艳等 (2011)利用S波反演得到的结果Q(f)=271.8×f0.5671。

表1 两次地震的震源破裂参数Tab.1 Source rupture parameters of two earthquakes

表2 随机有限断层法的基本参数Tab.2 Basic parameters of stochastic finite faults method

取苏中沿海1～10 Hz范围内的平均场地响应值2.739(詹小艳等，2011)，对合成地震动进行场地效应校正，最终得到东台、如皋及大丰3个台站的合成地震动峰值加速度分别为2.44、1.23、1.37 cm/s2，实际记录的地震动峰值则分别为2.62、1.28、1.85 cm/s2，两者十分接近;在剪切波的卓越持续时间、波形包络线的近似程度方面，东台、如皋2个台的结果与真实记录也十分相似(图3)，大丰台的相似度则较低，分析认为这可能与其距此次震中的距离较远和台基地下结构差异有关;3个台的合成地震动在5～15 Hz频带范围内、阻尼比为2%的反应谱计算结果与实际记录结果均基本一致，并且随着震中距的增加，反应谱在低频段的一致性更加明显，说明基于动力学拐角频率的合成地震方法具有更宽频带的优点，能够较好地反映出主震剪切波的主要特征，可适用于江苏地区。

1979年7月9日江苏溧阳发生M6.0地震，极震区 (Ⅷ度)实际的长轴为北西西向，而重度破坏区 (Ⅶ度)的长轴却是北北东向，两者的明显差异引起一些学者对地震断层判断的争议 (孙受成等，1980)，震后众多学者对其震源破裂参数做了详细的研究。笔者对溧阳地震合成地震动计算所需的震源破裂参数和断层滑动模型，采用被普遍接受的研究结果和方法来进行构建:胡连英等 (1997)对其震源机制解的研究认为，主震的断层面沿矛东断裂带发生右旋走滑错动、兼有正断层性质的倾滑错动;林邦慧等 (1982)利用P波频谱分析方法推算了地震断层的破裂长度约为19 km;王炜 (1984)由破裂长度和破裂速度进一步地推算了此次地震的地震矩，平均位错为0.53 m。子断层的尺度依据 Beresnev和 Atkinson(2002)提出的下式进行划分:

可得子断层的尺度为2×2 km，并结合McGinty和Robinson(1999)的方法建立起主震断层面的滑动模型，如图4所示。

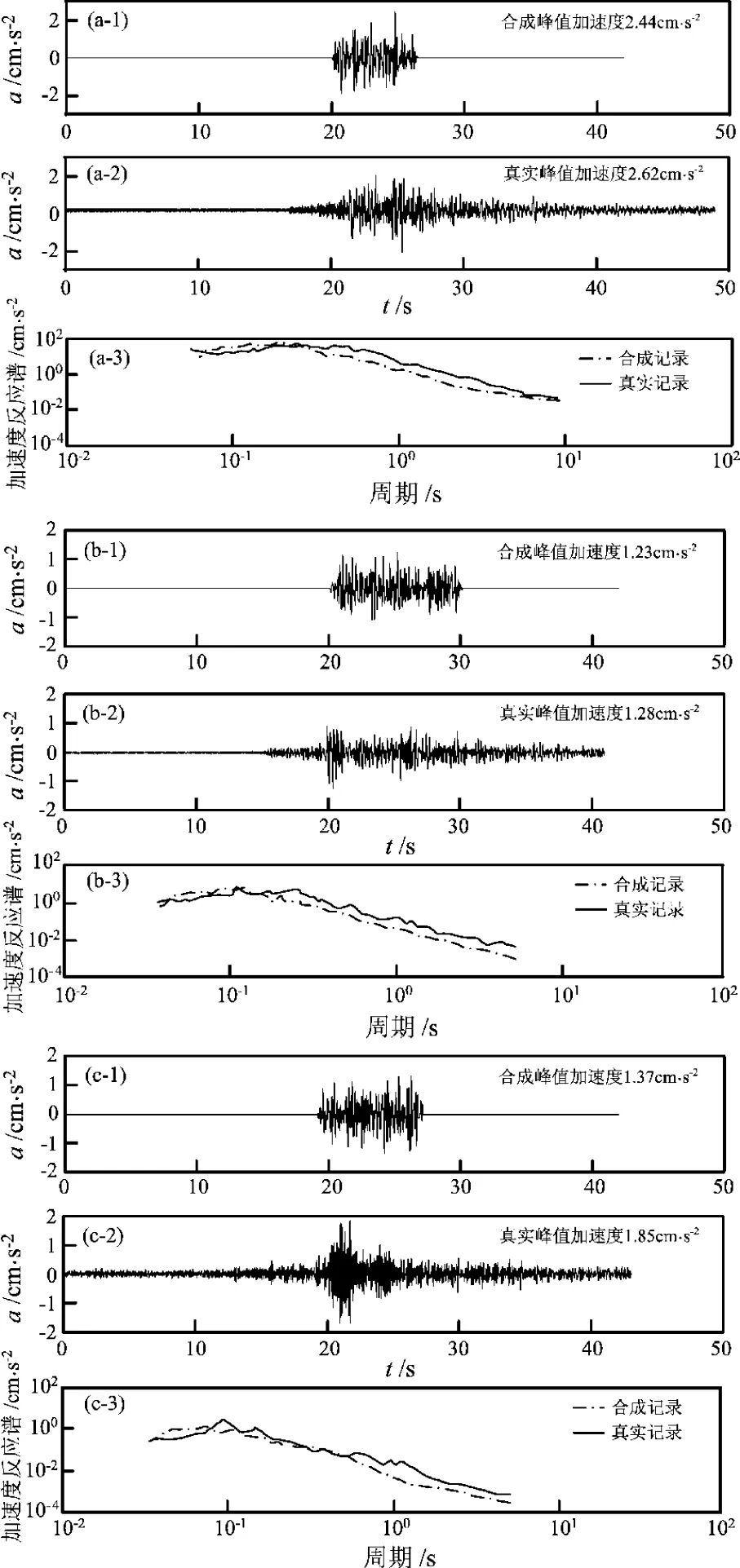
图3 东台(a)、如皋(b)及大丰台(c)的合成地震动和实际记录波形及阻尼比为2%的反应谱Fig.3 Synthetic ground motions and the actual waveforms recorded by Dongtai(a)，Rugao(b)，Dafeng(c)Stations，and their response spectrum of damping ratio is 2%

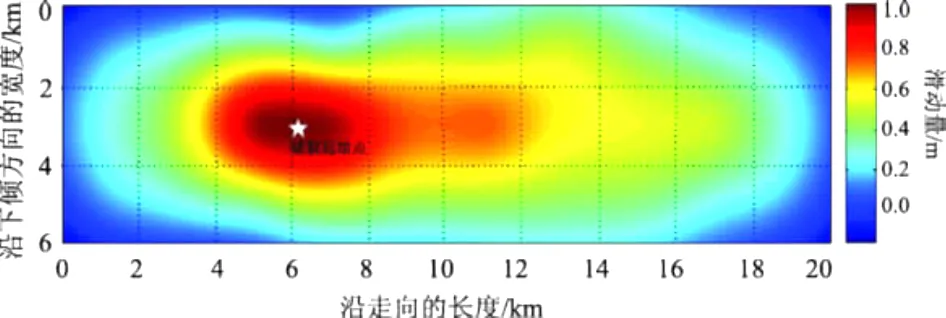
图4 溧阳M6.0地震的子断层及滑动模型Fig.4 Sub-faults and the sliding model of Liyang M6.0 earthquake

为了得到震源区 (31.1°～31.9°N，119.0°～119.7°E)基于合成地震动的烈度分布，如图2中矩形方框区域所示，需要获取震源区内一定数量的虚拟观测点的地震动记录。于是我们采用上述方法和震源参数来模拟得到溧阳地震震源区内156个节点处 (以0.06°为间隔)的地震动数值，并通过样条曲面插值方法进行内插值，最终得到其加速度场的分布。图5b显示峰值加速度大于180 cm/s2的区域长轴走向为近北北西向;而大于125 cm/s2的区域长轴走向为近北东东向，两者差异明显，这可能反映出极震区的合成地震动分布与震源的破裂模式有关。

3 地震烈度的划分

溧阳M6.0地震后，一些学者进行了大量的震害考察和科学评估，以《新的中国烈度表(1980)》为烈度线划分的依据得到了真实烈度分布 (胡连英等，1997):上沛西塘至庆丰为极震区，烈度达Ⅷ度，等震线长轴约7 km，呈北西西向，短轴为4.5 km，呈北北东向，总面积约为20 km2;Ⅶ度区主要是河口—旧县—东岳庙区域的一个规则椭圆，长轴走向为北北东向，面积约为389 km2;Ⅵ度区主要是社渚—金坛的似椭圆区域内，面积约为2 194 km2;Ⅴ度区的总面积约为10 945 km2，长轴为北北西向，如图5a所示。

为了检验基于合成地震动的地震烈度计算是否可行，是否可以运用在江苏地区今后的破坏性地震中，本文将采用2种划分方法来进行对比研究。一种为参考《新的中国烈度表 (1980)》中的物理指标来划分，即根据水平向的峰值加速度值，Ⅴ度时平均为31 cm/s2、Ⅵ度时平均为63 cm/s2、Ⅶ度时平均为125 cm/s2和Ⅷ度时平均为250 cm/s2，其结果如图5b中黑色线条所示。另一种则是采用袁一凡 (1998)提出的模糊评定方法，共分为8档，即:小于Ⅳ、Ⅳ、Ⅴ、Ⅵ、Ⅶ、Ⅷ、Ⅸ和大于Ⅸ。参与烈度计算的地震动参数主要为:(1)峰值加速度A:垂直峰值加速度和水平峰值加速度的比值作为一个独立的因子，当两者之比小于0.3时，烈度肯定小于Ⅸ度，因此它可以作为否定因子;(2)地震动的卓越频率; (3)20%的相对持时，即最初和最后到达峰值20%的两点间时间;(4)1、2、5、8 Hz频率点的反应谱值，其中5 Hz和1 Hz为主要值。但该方法的步骤较为复杂，且本文中经过内插值后虚拟场点的数量较多。因此，我们只计算了破坏最严重的Ⅵ和Ⅶ度区的分布，结果如图5b中红色线条所示。

由图5可以看出，基于合成地震动的两种烈度划分在相同的烈度区内基本重合 (图5b)，且与真实的烈度分布 (图5a)基本相符。通过比较可以看出采用模糊评定方法划分的Ⅵ度区，其长轴走向为北北东向、与真实烈度Ⅵ度区的长轴走向更为接近;Ⅶ度区的方向性不明显，真实烈度的Ⅶ度区长轴走向和极震区 (Ⅷ度区)的长轴走向差异明显，难以准确综合地判断其方向性;而基于峰值加速度评定的Ⅶ度区则是近“十”字形、长轴近北东东向;这表明模糊评定方法能更为真实地反映出各地震动参数与真实烈度之间的内在关系，更接近真实烈度的分布，体现了能综合不同因子来进行判定的优势。

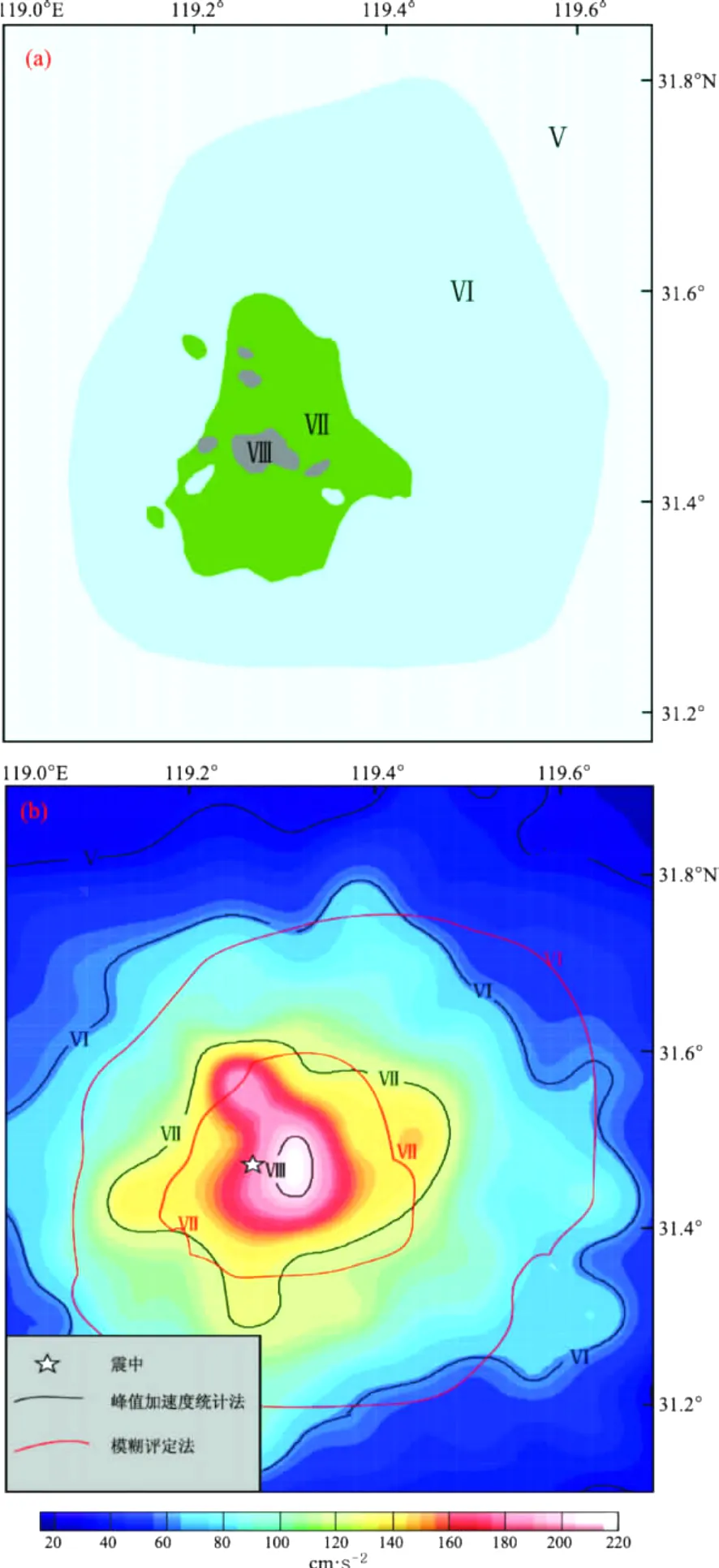
图5 溧阳M6.0地震的实际烈度 (a)(据胡连英等，1997)和合成地震动的理论烈度 (b)Fig.5 Actual intensity(a)(according to Hu et al，1997)and the theory intensity of synthetic ground motion based on two methods(b)of Liyang M6.0 earthquake

4 结论与讨论

从图5的计算结果来看，采用基于动力学拐角频率的合成地震动来划分烈度的方法，能够较为合理地反映出震源区的真实烈度分布。相比于地震烈度速报台网，通过合成地震动来实现震源区的烈度划分可能需要花费更长的时间，但仍可在震后获取到可靠的震源破裂参数后在数小时内完成，并可根据震源破裂参数不断地对结果进行修正，这比通过震后的震害考察评估来获得烈度分布速度快;目前我国大部分地区并不具备烈度速报的条件。因此，本文研究的快速理论烈度划分方法，能为将来破坏性地震发生后获取烈度分布提供参考，其现实意义是显著的。

地震动的模拟结果取决于震源、传播路径及场地3个物理过程的模型建立，本文中震源的断层滑动模型是根据McGinty和Robinson(1999)计算静态库仑应力触发时所采用的平均错动方法而建立的，模型的简化可能会造成计算结果的一些误差;在对合成地震动进行场地效应校正时，采用的是区域平均场地效应值，这与场点的真实场地响应有一定差异。此外，本文只计算了一种破裂方法的地震，在结果的普遍性上受到了限制，因此在今后的研究中还需要对不同震源模型、破裂模式、震级规模的地震进行研究。

崔建文，卢大伟，高东，等.2008.基于合成地震的震区烈度划分［J］.地震研究，31(4):387－393.

胡连英，徐学思，孙寿成，等.1997.溧阳地震与茅东断裂带［M］.北京:地震出版社.

黄耘，李清河，孙业君，等.2006.江苏及邻区地壳上地幔结构研究［J］.西北地震学报，28(4):369－376.

李山有，金星，陈先，等.2002.地震动强度与地震烈度速报研究［J］.地震工程与工程震动，22(6):1－7.

林邦慧，魏富胜，刘万琴，等.1982.溧阳—介林—五原北西地震带强震的破裂特征［J］.地震学报，4(2):14－24.

石玉成，陈厚群，李敏，等.2005.随机有限断层法合成地震动的研究与应用［J］.地震工程与工程震动，25(4):18－23.

孙受成，徐学思，胡连英.1980.溧阳地震［J］.地震，1(1):32－36.

王海云，谢礼立.2009.近断层强地震动场预测［J］.地球物理学报，52(3):703－711.

王炜.1984.溧阳地震前震中分布集中度C的变化［J］.地震科学研究，2(2):89－94.

袁一凡.1998.由地震动三要素确定地震动强度(烈度)的研究［R］.北京:国家地震局工程力学研究所.

詹小艳，许红梅，王俊，等.2011.江苏地区的介质非弹性衰减和场地响应研究［J］.地震地磁观测与研究，32(6)，20－27.

Aki K，Richaids P G.1986.定量地震学［M］.北京:地震出版社.

Atkinson G M，Beresenev I A.2002.Ground motion at Memphis and St.Louis from M7.5－8.0 earthquakes in the New Madrid seismic zones［J］.BSSA，92(3):1 015 － 1 024.

Beresnev I A，Atkinson G M.1997.Modeling finite-fault radiation from the ωn spectrum［J］.BSSA，87(1):67 －84.

Beresnev I A，Atkinson G M.1998.FINSIM －a FORTRAN program for simulating stochastic acceleration time histories from finite faults［J］.Seism Res Let，69(1):27 － 32.

Beresnev I A，Atkinson G M.2002.Source parameters of earthquakes in eastern and western North America based on finite-fault modeling［J］.BSSA，92(2):695 －710.

Boore D M.1983.Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra［J］.BSSA，73(6A):1 865－1 894.

Brune J.1970.Tectonic Stress and spectra of seismic shear waues from earthquake［J］.JGR，75(26):4997 ～ 5009.

Hanks T C，McGuire P K.1981.The character of high frequency strong ground motion［J］.BSSA，71(6):2 071 －2 095.

Hartzell S H.1978.Earthquake aftershocks as Green's functions［J］.Geophys Res Lett，5(1):1 － 4.

Irikura K.1983.Semi-empirical estimation of strong ground motions during large earthquakes［J］.Bull Disaster Prevention Res Inst(Kyoto Univ)，33(298):63 －104.

McGinty P，Robinson R.1999.Silp distribution of Lake Tennyson earthquake，New Zealand，as inferred from static stress changes and off fault aftershocks［J］.Geophysical Research Letters，26(13):1 961－1 964.

Motazedian D，Atkinson G M.2005.Stochastic finite-fault modeling based on a dynamic corner frequency［J］.BSSA，95(3):995 － 1 010.

Somerville P，Sen M，Cohee B.1991.Simulations of strong ground motions recorded during the 1985 Michocan，Mexico and Valparaiso，Chile，earthquake［J］.BSSA，81(1)，1 －27.

Zafeiria R，Beresnev I A.2003.Stochastic finite-fault modeling of ground motions from 1999 Chi-Chi，Taiwan，earthquake:Application to Rock and Soil sties with Implications for Nonlinear Site Response［J］.BSSA，93(4):1 691 －1 702.

Computational Research on the Seismic Intensity Based on Stochastic Finite Faults Method

WANG Jun，HUO Zhu-qing，ZHAN Xiao-yan，SONG Hao，JIANG Hao-ling，XU Ge
(Earthquake Administration of Jiangsu Province，Nanjing 210014，Jiangsu，China)

Firstly，using stochastic finite faults method based on the dynamic corner frequency，we simulated the synthetic ground motion of Dongtai M3.8 earthquake，Jiangsu in 2006 recorded by Dongtai，Rugao and Dafeng stations and compared synthetic ground motion with the actual ground motion recordings.We find that the synthetic ground motion using improved stochastic finite faults method can better reflects the main features of shear wave of main shock in Jiangsu area.Secondly，we apply this method to simulate the synthetic ground motion of 156 virtual observation points in source region and got the distribution of synthetic acceleration field of Liyang M6.0 earthquake in 1976.Thirdly，we respectively calculated the theoretical distribution of seismic intensity by peak acceleration statistical method and fuzzy evaluation method.The results showed that the intensity classification results by two methods essentially consistent with that of the actual investigation.However，intensity classification result by the fuzzy evaluation method is more consistent with distribution of actual intensity.

dynamic corner frequency;stochastic finite faults method;synthetic ground motion;seismic intensity;Liyang M6.0 earthquake

P315.9

A

1000－0666(2012)03－0374－07

2011－08－18.

国家自然科学基金项目 (41074036)和江苏省地震局青年基金 (10420)联合资助.