随机环境马氏链下熵的极值问题的研究

宁小青，郭光耀

(武汉工程大学 理学院，湖北 武汉 430073)

1 随机环境马氏链下的有关的熵

设{Xn,n≥1}为状态有限的随机环境马氏链，相关定义及其性质，参见文献[1-9]，且满足π遍历，E=m，Ui={Φ}，∧(M)=1，本文将研究与{Xn,n≥1}有关的熵有关的极值问题.

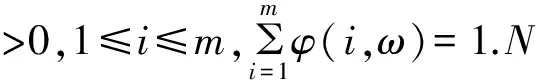
Pn(ω;i,j)=P(ω0,…,ωn-1;i,j).

对任意的i,j∈{1,2,…,m}，n=1,2,…，ω∈Ω，令:

En′=((i,j):i,j∈E,P(ωn+1;i,j)>0,n≥1)；ξ=(ξ(1),ξ(2),…,ξ(n))；ξ(n)=(ξij(n),(i,j)∈E′)；

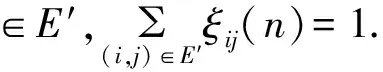
且满足，∀1≤n有:

Ci(ξ(1))=Ci(ξ(2))=…=ri(ξ(1))=ri(ξ(2))=…

(1)

若ξ满足条件式(1)，则记ri(ξ(n))=ri(ξ).

2 概率空间上有关测度与维数的定义

首先，引入概率空间上Hausdorff测度与Hausdorff维数的有关定义.假定{Xn,n≥1}是定义在概率空间(Ω,F,μ)上取值于有限或可列的状态空间E的随机过程，令Ia1,…,an={ω∈Ω:Xk=ak,k=1,2,…,n}，其中(a1,a2,…,an)∈En，称Ia1,…,an为n阶柱集，记In(ω)=:IX1(ω),…,X2(ω)，显然，这是包含ω的n阶柱集，约定零阶柱集I0(ω)=Ω.

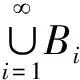
定义1Φ恒表示满足下列条件的函数φ所成的类：

1)φ:(0,δ)→(0.),(δ>0)，

2)φ是单增，右连续的，且φ(0+)=0.

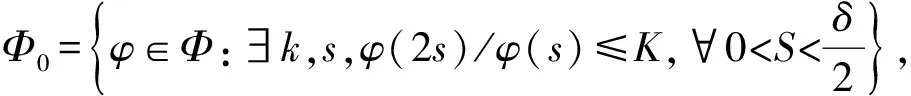
定义2 任取φ∈Φ，M⊂Ω，0<δ<1，令:

Lμ(M,φ,δ)=inf{∑φ(μ(Bi)){Bi,i≥1}是M的一个μ-σ-覆盖}，

则称Lμ(M,φ)是集合M关于测度函数φ的Hausdorff测度，特别地，当φ(x)=xα时，分别记此时的Lμ(M,φ,δ)，Lμ(M,φ)为Lμ(M,α,δ)与Lμ(M,α)容易得到，当Lμ(M,α)<时，∀ε>0，总有Lμ(M,α+ε)=0，故存在α0=inf{α:Lμ(M,α)=0}=sup{α:Lμ(M,α)>0}，称此α0是M的Hausdorff维数，记为dimμ(M).在不引起混淆的情况下，以上符号可分别写为：L(M,φ,δ)，L(M,φ)，L(M,α,δ)，L(M,α)，dim(M).

类似，可以定义填充测度与填充维数Dim(M)等，参见文献[5，8].

b)3条件熵的极值相关结论及证明

若令M(ξ)={ω∈Ω:δ(ω,n;i,j)→ξij,∀(i,j)∈E′}.B={一切满足条件1)的所有组合的集合，∀1≤i≤m},M(S)={ω∈Ω:∃ξ∈S使δ(ω,n;i,j)→ξij，∀(i,j)∈E′}，则按照上面条件熵与Hausdorff测度与Hausdorff维数及填充测度与填充维数的有关定义与性质，可以得到ξ的条件熵的极值与M(S)维数之间有下面的关系.

i)dimμ(M(S))=Dimμ(M(S));

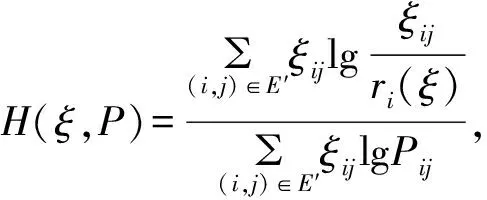
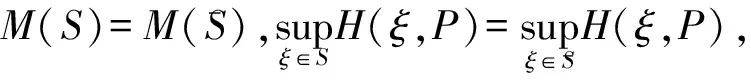
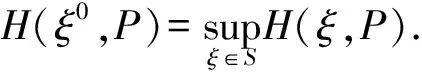
首先定义一个随机环境马氏链下转移矩阵如下：

则(C1(ξ0),…,Cm(ξ0))是η(ωn;i,j)的平稳分布，事实上:

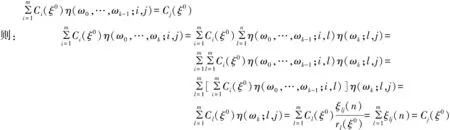
故{Xn,n≥1}是定义在(Ω,F,v)上以(η(ω0,…,ωn-1;i,j))为转移矩阵且具有平稳分布(C1(ξ0),…,Cm(ξ0))的随机环境马氏链.

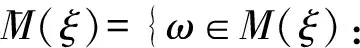
往证：

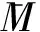
仿照文献[5]，易证：

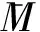
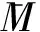
故:

(2)

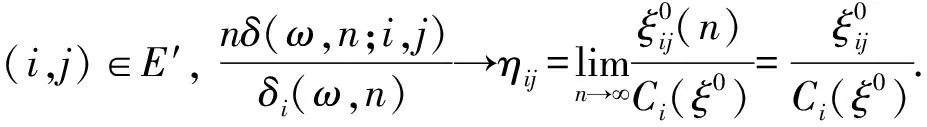
例2：K=3，L=7时，的最小长度是十次采样，图2说明了几种解法中的一种。可以看出，小波并不像前一个例子那样光滑，但是对于负频率更接近于零。这是可以预测的，由于我们降低了消失矩的阶数，同时改进了半采样延期的近似值。

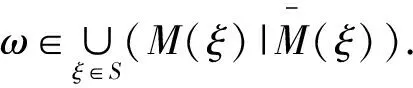
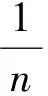
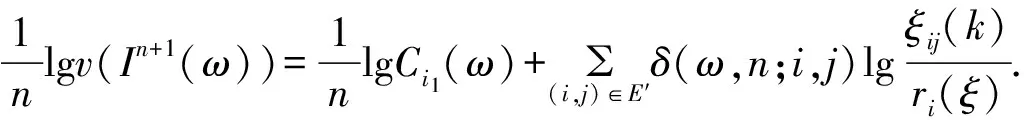
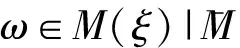
利用求条件极值可以得到:

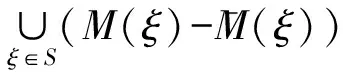
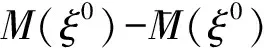
[1] Cogburn R.Markov chains in random environments:the case of Markovian environments[J].Ann Prob,1980,8:908-916.

[2] Chung K L.Markov chains with stationary transition probabilities[M].New York:Spring-Verlagm,1960.

[3] 胡迪鹤.The existence and moments of canonical branching chain in random environments[J].Act Mathematica Scientia,2004,24B(3):499-506.

[4] 胡迪鹤.随机过程论——基础理论运用[M].武汉：武汉大学出版社,2002.

[5] 郭光耀，张超杰，娄联堂.随机环境马氏链上一类集合的分形维数[J].武汉大学学报:理学版,2006，52(3)：277-280.

[6] 李应求.关于马氏环境中马氏链的几点注记[J].数学进展，1999,28(4)：358-360.

[7] 李应求.状态可数的马市环境中马氏链函数强大数定律[J].数学杂志，2003,23(4)：484-490.

[8] 宁小青，郭光耀.随机环境马氏链下弱遍历性及其应用[J].湖北民族学院学报：自然科学版,2012，30(1)：45-48.

[9] 宁小青.有限状态下随机环境马氏链的性质[J].三峡大学学报:自然科学版,2011(8):695-701.

[10] 傅祖芸.信息论——基础理论与运用[M].2版,北京:电子工业出版社,2007.

[11] 傅祖芸.赵建中.信息论与编码[M].北京:电子工业出版社,2006.

[12] 邓稼先.康耀红.信息论与编码[M].西安:西安电子科技大学出版社,2007.

[13] 杨卫国.可列非齐次马氏链熵率的存在定理[J].数学的实践与认识,2011(2):86-90.