无人机影像的快速拼接及其误差

刘庆元，刘 有，邹 磊，易柳城

(1. 中南大学 有色金属成矿预测教育部重点实验室，长沙 410083；2. 中南大学 地球科学与信息物理学院，长沙 410083)

随着无人机的广泛应用，各种影像和视频影像的获取更加方便和及时，但影像的及时处理和初步定位显得越来越重要。无人机影像特点不同于航空影像，其重叠度较高，倾角大、像幅小，目前现有的影像处理软件处理不了这种大倾角影像，只有通过地面具有足够的控制点加以纠正，通过航摄处理方法变为正射影像图，再进行拼接。而在地质勘查、地质灾害、危机处理、以及抢险救灾等应用中，并不需要大比例尺影像图，只需要能够反映当前地物、地貌形态以及地理位置就完全可以满足要求。

无人机影像的快速匹配、拼接和纠正处理可分为两类，一是在不需要地面控制点的情况下，对已有影像配准后进行拼接和纠正处理，由于没有考虑投影差对影像拼接时的影响，使拼接误差积累较快，同时没有考虑影像间尺度的变化[1−6]；二是针对无人机影像特点参照传统的摄影测量流程进行的处理，这样处理的结果精度比较高，但同时需要有高精度的姿态参数和地面像控点，出图周期长、不利于实时应用[4−12]。

本文作者主要利用DGPS/IMU 数据，在没有地面像控点的情况下，实时进行影像(每个像对)匹配，匹配过程中通过左右像对上下视差的计算，剔除有较大误差或错误的特征点，并充分利用DGPS坐标获取整体影像地理坐标值的同时考虑影像尺度的变化，通过限制和消除投影误差的办法，减少拼接时的误差累积。

1 实验

无人机影像特点不同于航空影像，其重叠度较高，倾角大、像幅小，在单位时间内地面变化小，但影像之间往往存在着平移、旋转和较小尺度的缩放。通过匹配同名点，运用仿射变换和粗差剔除的方法实现影像快速拼接，可获取被拍摄区域影像图。假定待拼接影像之间存在平移、角度旋转和尺度变化等参数，则影像间的变化关系可用式(1)表达。

式中：(x, y)为变换后坐标；) ,(yx′′为变换前的坐标；a0、a1、a2、b0、b1和 b2为转换参数。

此方程组仅需要3个同名像点即可求解出6个参数。由于实际操作中可以获得大量的同名像点，因此，采用最小二乘法求解加粗差检验的方法可获取转换参数。

1.1 无人机影像的主要误差

按上述方法拼接影像是否成功取决于拼接的误差大小。影响影像拼接的主要误差包括由外方位元素变化引起的影像变形误差、地形起伏引起的影像变形误差以及地球曲率和大气折射引起的影像变形误差。由于无人机距离地面比较低，地球曲率和大气折射引起的影像变形误差影响较小，可以忽略。当影像经过外方位角元素组成的旋转矩阵转换后，影像处于近似水平状态，这时主要的误差为投影误差。如果被拍摄地面比较平坦，投影误差较小，影像可直接进行拼接，否则，需要对投影误差较大的同名点进行改正。

图1 单幅影像上由地面高程引起的像点位移Fig. 1 Image point displacement due to surface height changes

图1所示为单幅影像上由地面高程引起的像点位移。由图1可见，点a与a′之间的距离d为地物高度引起的投影误差。A′A″即为地面上的投影差，用D表示。假设像片上从像主点到地物顶部的距离是 r，投影到基准面上的相应距离为 R。则根据相似三角形AA′A″和 SOA″得

式中：D是投影误差；h为高出基准面的地面高差；H为航高；R为地面摄影中心到地物点的距离。

由式(2)可以看到，影响投影误差的主要因素是航高与地面高差。

以像片的比例尺表达距离D和R，并考虑到左(l)、右(r)两片具有相同的性质，重新整理得到

下面讨论两张相邻影像的情况。如图 2所示，O1、O2为摄影基线在地面投影的长度。显然，地面物体的顶部A在两次拍摄时分别被投影到1A′′和2A′′，21AA′′′′即为同一地面点在两次拍摄时由h产生的投影误差，其差值记为ΔD。三角形21AAA′′′′′和21OOA′相似，考虑式(2)和式(3)，假定左右两片航高相等，并将ΔD化为图上距离Δd得到

由式(4)可以大致估计出两张相邻影像投影误差Δd，用作判断拼接影像效果的依据。即当制作 1∶2.5万影像图时，航高600 m，摄影焦距0.024 m，摄影基线长度 S=30 m，地面高差 h=40 m，代入式(4)得Δd=0.085 mm。这表明此高卷在1∶2.5万的影像图中不会影响图的使用；若地面高差h=100 m时，代入式(4)得 Δd=0.24 mm，则在1∶2.5万影像图上可以分辨出它们的差异。由此可以看出，航高、基线长度以及高出基准面的地面高差均对投影误差有一定的影响，在处理影像拼接时需要考虑到这些影响，并采取不同的方法加以削弱。

由 DGPS/IMU提供的初始外方位线元素和角元素，再经连续相对定向后，构成共面方程求解各点的地面三维坐标值。将各点Z值取平均获得平均高程，各点与平均高程之差即为h；当h大于投影误差时可根据式(3)分别求得左片与右片的改正量d，分别对左右片的像点坐标进行改正。

1.2 无人机影像快速拼接的方法

1.2.1 平坦地区影像拼接方法

由上面分析可知，影像拼接时将影像分为平坦地区和丘陵山区，所使用的方法会有所不同。由于平坦地区投影差较小，可以不进行投影误差改正，在不需要任何外在条件的基础上，直接利用左右影像同名像点进行影像拼接。具体方法是：将航线中第一张(左片)影像进行畸变差改正后和利用式(5)，将左片像空间坐标转为像空间辅助坐标系的坐标，这样此片近似处于水平状态，然后将右影像像空间坐标代入式(1)，求得右像空间坐标系转换为左像辅助空间坐标系的转换系数 a0、a1、a2、b0、b1和 b2。用此系数将右片所有像点转换为左片坐标系的坐标，如图3所示，左右两片的坐标原点均在各自的左上角，即栅格数据的坐标原点。以此类推，转换系数求解到最后一张影像为止。由于同名点较多，用式(1)求解转换系数时，按式(6)最小二乘原理进行求解，所获残差V代表同一点左、右两影像点的坐标差值，其量应小于0.1 mm，如果存在大于2倍的误差时，可怀疑此点匹配误差较大或者影像变形较大，将影响两片的拼接效果，可以剔除该点重新计算转换系数，减小误差积累。

图2 像对上像点的相对位移(俯视图)Fig. 2 Same object project onto different frames (Looking down at surface)

式中：[X Y Z]T是左片像空间辅助坐标系的坐标；R为旋转矩阵；x、y、z为左片像空间坐标系坐标。

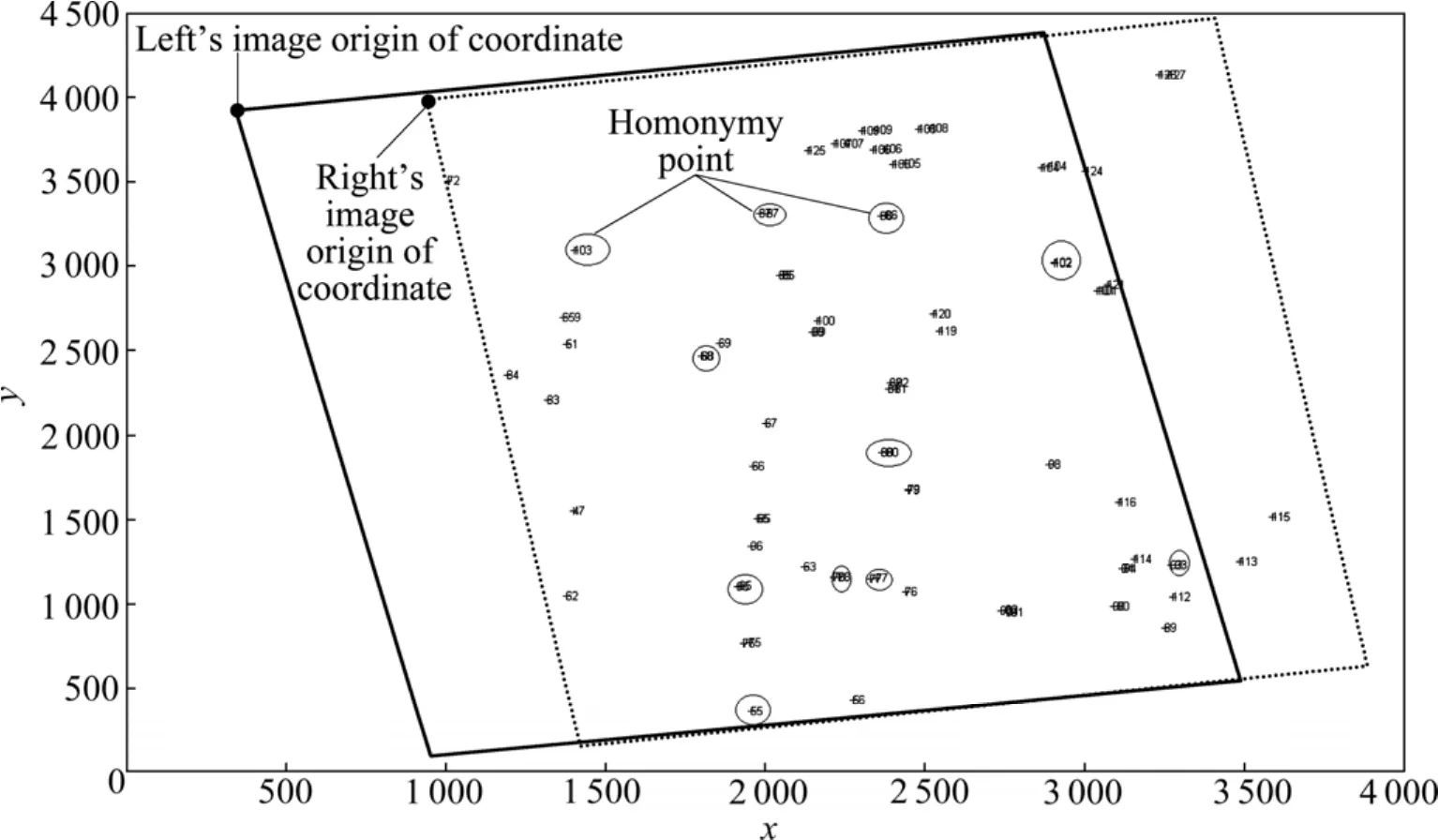
图3 左、右影像坐标原点与同名点示意图Fig. 3 Homogenous points on right image matched with those on left image

影像拼接时配合匹配软件进行相对定向，剔除上下视差较大的匹配点，在不需地面像控点的情况下，直接进行影像拼接工作，拼接可实时或事后进行。在拼接影像的同时，根据GPS/IMU获得的外方位元素，同时进行同名点初步的地理坐标计算，使各个模型在此基础上连接起来，在影像重采样时用地理坐标代替像素坐标，使整幅影像具有与GPS一致的坐标值。

1.2.2 丘陵山区影像拼接方法

在丘陵山区因为投影误差的影响，影像拼接的误差累积较快。此时应采用分带拼接，即在保证影像完整的前提下通过几何纠正使其投影误差在该区域内消弱，避免向下传递。先利用双线性变换公式(9)，使右片的像点坐标在坐标转换过程中以左片像点为准，对右片的同名像点在转换过程中较大的投影误差点进行几何纠正，使其两个坐标间的差值变小，而局部随地形的变化产生一定的形变，达到在视觉上将影像拼接的目的。因此，拼接时的影像个数应有所限制，将这些分段拼接影像再通过式(1)的仿射变换连接起来，形成整幅影像图。

2 应用实例

实例1 中国某地2008年实地航拍，航高600 m，影像尺寸3 888×2 596(像素)。DGPS/IMU给出摄影外方位元素值，角元素精度为 60″，线元素精度为 20～10 m，GPS更新率为1 Hz。实际地形大部分比较平坦，靠近河流部分有些小山。拼接按每条航线进行，每片与左、右片的同名点由专用影像点匹配软件自动进行，匹配后拼接工作也是自动进行。在拼接过程中观察的主要指标是残差 V(residual error)和中误差 RMS(Root mean square)，对于超出中误差2～3倍的V值对应的同名点给予剔除，消除由于匹配点不准引起的粗差。拼接效果见图 4，残差见表1。

表1 36张UAV影像连续自动拼接RMS一览Table 1 RMS errors of hill area test for 36 pieces of UAV’s images

实例2中国某城市，航高600 m，影像尺寸4 000×3 000(像素)。没有DGPS/IMU数据，地形主要特点是楼房较高，地面平坦。对于影像拼接楼房的投影差较大，是影响拼接的主要障碍。但其有利条件是除了楼房之外地面较为平坦，对影像拼接比较有利。拼接的关键是剔除楼房顶端的投影误差较大的匹配点，拼接效果见图5。

图4 36张UAV影像连续自动拼接效果图Fig. 4 36 pieces of UAV’s images stitched together

图5 9幅UAV影像连续自动拼接效果图Fig. 5 9 pieces of UAV’s images stitched together

实例2与实例1的区别在于，没有内、外方位元素，不能进行投影差改正和影像倾斜纠正。拼接过程中第一张影像的选取至关重要，要选取基本水平影像作为起始影像，另外，要在拼接过程中剔除较大的 V值点，始终保持其左、右片同名点基本上在平坦地面上的点。拼接后的中误差值见表2。

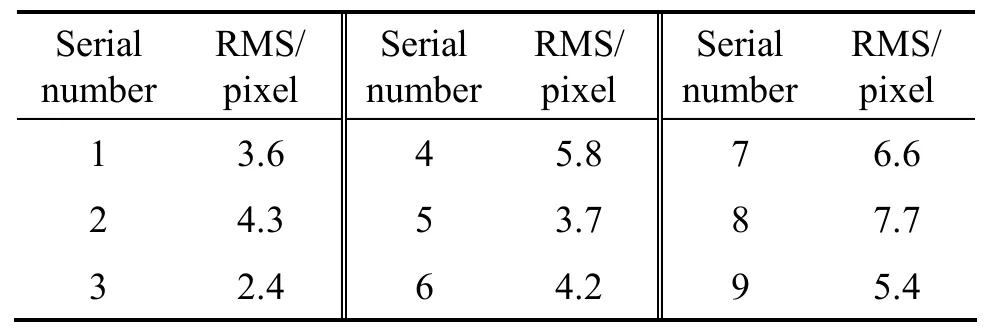
表2 9幅UAV影像连续自动拼接中误差一览Table 2 RMS errors of urban test for 9 pieces of UAV’s images

通过上面两个实例说明当匹配点有足够多时，通过最小二乘方法求仿射变换转换系数，既可以保证坐标传递的正确性和拼接的连续性也可以抑制粗差对拼接的影响，保证拼接的正确性。另一方面，通过最小二乘解算时的两个指标V和RMS的观察找到误匹配点和投影误差较大的点，在快速拼接过程中迅速剔除，小于规定值的投影误差进行改正，保证坐标传递的正确性。

3 结论

1) 若投影误差 h≈0，则Δd趋近于 0；Δd是一个与地物高度和航高有关的量，h越大，则位移Δd越大，H越大，则Δd越小。当地物高于基准面时，Δd沿着r向主点方向改正，否则，沿着r逆着主点方向改正。

2) 拼接影像的同名点尽量选择平坦地点上，使同名点的高度尽量小。对于处在高程较高位置的同名点进行改正。城市去根据V和RMS两个指标，将具有较大投影误差点(高楼顶部的点)剔除，保留城市地面匹配同名点，拼接效果较好。

3) 尽量增大航高，可以减小像点的投影误差；尽量减小摄影基线的距离，即增加遥感影像的航向重叠度，也可以使像点的投影误差减小。

4) 如果没有GPS/IMU的数据，拼接时主要靠观察V和RMS大小，决定同名点的取舍。

[1] 宫阿都, 何孝莹, 雷添杰, 李 京. 无控制点数据的无人机影像快速处理[J]. 地球信息科学学报, 2010, 12(2): 254−260.

GONG A-du, HE Xiao-ying, LEI Tian-jie, LI Jing. Fast image processing method of UAV without control data [J]. Journal of Geo-Information Science, 2010, 12(2): 254−260.

[2] 赵向阳, 杜利民. 一种全自动稳健的图像拼接融合算法[J].中国图象图形学报, 2004, 9(4): 417−422.

ZHAO Xiang-yang, DU Li-min. An automatic and robust image mosaic algorithm [J]. Journal of Image and Graphics, 2004, 9(4):417−422.

[3] 王书民, 张爱武, 崔营营, 张珍梅. 基于无人飞艇数字摄影测量系统及航拍序列图像拼接[J]. 测绘科学, 2010, 35(4): 81−83.

WANG Shu-min, ZHANG Ai-wu, CUI Ying-ying, ZHANG Zhen-mei. Digital photogrammetry system based on unmanned airship and aerial image sequence stitching [J]. Science of Surveying and Mapping, 2010, 35(4): 81−83.

[4] 鲁 恒, 李永树, 何 敬, 陈 强, 任志明. 一种基于特征点的无人机影像自动拼接方法[J]. 地理与地理信息科学, 2010,26(5): 16−19.

LU Heng, LI Yong-shu, HE Jing, CHEN Qiang, REN Zhi-ming.A automatic mosaic method in unmanned aerial vehicle images based on feature points [J]. Geography and Geo-Information Science, 2010, 26(5): 16−19.

[5] 徐亚明, 邢 诚, 陈晓东. 一种基于拼接线的无人机序列影像拼接方法[J]. 武汉大学学报: 信息科学版, 2011, 36(11):1265−1269.

XU Ya-ming, XING Cheng, CHEN Xiao-dong. A mosaic method for UAV sequence images based on seam line [J].Geomatics and Information Science of Wuhan University, 2011,36(11): 1265−1269.

[6] 苏俊英. SIFT特征匹配无人飞艇多光谱影像拼接[J]. 应用科学学报, 2010, 28(6): 616−620.

SU Jun-ying. SIFT mosaicing of multiple spectrum images acquired from unmanned airship with SIFT feature matching [J].Journal of Applied Sciences, 2010, 28(6): 616−620.

[7] 潘 俊, 王 密, 李德仁. 基于顾及重叠的面 Voronoi图的接缝线网络生成方法[J]. 武汉大学学报: 信息科学版, 2009,34(5): 518−521.

PAN Jun, WANG Mi, LI De-ren. Generation of seamline network using area Voronoi diagram with overlap [J]. Geomatics and Information Science of Wuhan University, 2009, 34(5):518−521.

[8] 张剑清, 孙明伟, 张祖勋. 基于蚁群算法的正射影像镶嵌线自动选择[J]. 武汉大学学报: 信息科学版, 2009, 34(6):675−678.

ZHANG Jian-qing, SUN Ming-wei, ZHANG Zu-xun.Automated seamline detection for orthophoto mosaicing based on ant colony algorithm [J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 675−678.

[9] 刘凤德, 邱 懿. 基于左右正射影像的三维量测方法的研究[J]. 测绘科学, 2003, 28(3): 17−19.LIU Feng-de, QIU Yi. 3D measurement based on ortho-image pair [J]. Science of Surveying and Mapping, 2003, 28(3): 17−19.

[10] 杨 林, 张 卡, 盛业华, 闾国年. 数字图像的两种影像拼接方法及其比较[J]. 计算机应用研究, 2005, 5: 135−136.

YANG Lin, ZHANG Ka, SHENG Ye-hua, LÜ Guo-nian. Two methods of digital image merging and their contrast [J].Application Research of Computers, 2005, 5: 135−136.

[11] 李 奇. 数字正射影像拼接的研究[J]. 地理空间信息, 2005,3(1): 10−11.LI Qi. Research of digital orthophoto maps mosaic [J].Geospatial Information, 2005, 3(1): 10−11.

[12] 尤红建, 刘 彤, 刘少创, 李树凯. 利用3维成像仪快速生成遥感地学编码图像[J]. 测绘学报, 2000, 29(4): 324−328.

YOU Hong-jian, LIU Tong, LIU Shao-chuang, LI Shu-kai. Fast generating geo-referenced image based on airborne 3D imager[J]. Acta Geodaetica et Cartographica Sinica, 2000, 29(4): 324−328.