沟道二维泥石流运动和冲淤数值模型研究

张万顺，赵琰鑫，崔鹏，彭虹，陈雪娇

(1.武汉大学资源与环境科学学院，430079，武汉;2.中国科学院成都山地灾害与环境研究所，640041，成都;3.武汉大学水利水电学院，430072，武汉)

泥石流是山区特有的一种自然地质现象，它是在降水、地形地貌、地质构造、固体堆积物、植被覆盖度及人类活动等多种因素共同作用下，发生在沟谷或山坡上的一种挟带大量泥砂、石块和巨砾等固体物质的特殊洪流，具有高密度、高流速、高流量、短历时和宽级配等特征［1］。泥石流高速运动方式往往给泥石流影响范围内的房屋、桥梁等造成毁灭性的破坏，同时伴随着泥石流运动过程大量颗粒物质的搬运和堆积，可以在短时间内对沟道形态演变产生巨大的影响，主要表现在在沟道上游强烈下切，导致滑坡和崩塌活动，而沟道下游由于不同程度的淤积，造成大片农田、铁路、公路严重受灾。泥石流的运动过程和沟道内冲淤过程的数值模拟研究对泥石流灾害防治具有非常重要的作用。

目前研究中采用的泥石流动力学模型可分为2大类:一类是具有统一内在屈服应力和黏性的单一相或伪一相流体模型，包括宾汉体模型［2］、膨胀体模型［3］及混合流体模型［4］;另一类是两相流体模型［5］，即把泥石流体中的浆体(由固相中的细颗粒和液相水组成)和粗颗粒各视为一种流体。近年来，泥石流数值模型研究工作已经取得了一定进展。王光谦等［5］将泥石流浆体用宾汉体模型、粗颗粒用膨胀体模型分别进行描述，建立泥石流的两相流二维模型。余斌［6］利用宾汉体模型，应用固液两相的混合流方程对泥石流进行数值模拟，计算了河床底部有凸台情况下的泥流分布。张万顺等［7］以水沙混合流为基础建立了适合泥石流模拟的二维非恒定流模型，研究泥石流运动和主河交汇的相互作用。以上研究对于沟道泥石流运动模拟进行了积极的探索，但是仍然存在不足，对阵性非恒定泥石流运动演进过程研究较少，特别是缺乏对沟道的冲淤及其与泥石流运动过程之间的关系的描述，不能够系统地、定量地模拟研究泥石流运动影响下沟道的冲淤动态过程。

笔者以水沙混合流模型为基础，采用混合流沙量动态变化模式，导出泥石流运动控制方程组，建立适于模拟沟道泥石流的二维非恒定数值模型。利用建立的数值模型，模拟云南蒋家沟流域典型泥石流动态演进过程和沟道的冲淤演变，不仅具有一定的理论意义，也可为流域泥石流风险预测和灾害治理提供参考。

1 泥石流运动模型

从宏观上，泥石流是水沙的混合流体，在演变过程中由于水沙的含量不同，表现出塑性蠕动流、黏性阵流、阵性连续流和稀性连续流等不同运动形态;从微观上，泥石流属于固液两相流。但若直接采用两相流模型，则泥石流固液两相间的相互应力作用力难以具体地加以量化，实际应用中还存在很大的困难。笔者采用的泥石流运动模型以水沙混合流模型为基础，可以避免考虑两相间的微观作用力，同时也可以利用已有的泥石流的应力或阻力的研究成果。

1.1 基本方程

连续性方程

动量方程

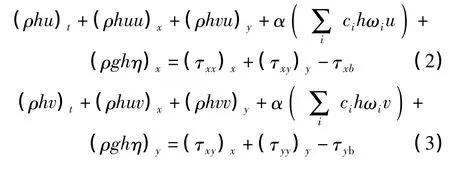
泥沙对流扩散方程

河床变形方程

床沙级配调整方程

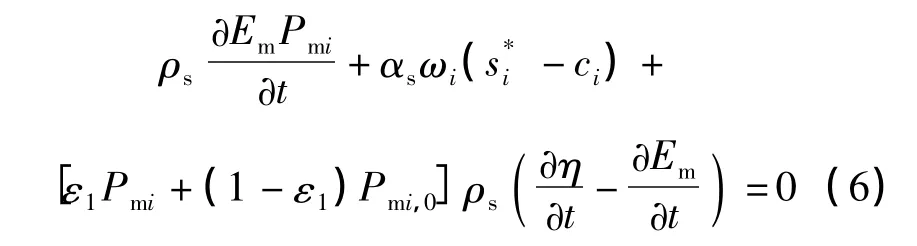
式中:u、v 为x、y 方向的速度分量，m/s;h 为泥石流深，m;zb为沟床高程，m;η 为泥石流自由表面高程，m;ci为第i 组泥沙的含沙量，kg/m3;ωi为第i 组泥沙的沉降速度，m/s;ρs为泥沙密度，kg/m3; ρ 为泥石流混合密度，kg/m3为水密度，kg/m3;εs为泥沙的紊动扩散系数，m2/s;Em为混合层厚度，m;αs为混合流饱和泥沙恢复系数，m2/s;s*i 为混合流对i 组泥沙的挟沙力，kg/m3;ε1为模型参数，当泥石流冲刷到原始河床时ε1=0，否则ε1=1;Pmi为床沙i 组泥沙的比例，%;Pmi，0为原始床沙i 组泥沙的比例，%;g 为重力加速度，m/s2;α 为积分形状系，α=1;τxb、τyb分别为泥石流运动在x、y 方向床面的切应力分量，N/m2，计算公式为:

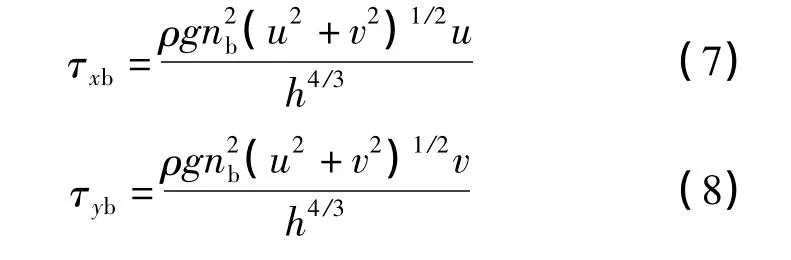
式中:nb为河床糙率; τxx、τxy和τyy为泥石流切应力分量，N/m2，计算公式分别为:

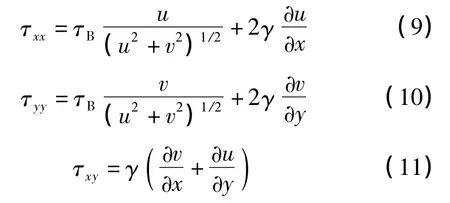
式中:τB为泥石流宾汉结构应力，N/m2;γ 为泥石流宾汉体的黏滞系数，N·s/m2。

1.2 模型辅助方程

1.2.1 泥石流宾汉结构应力模型 泥石流宾汉结构应力τB是泥石流的网格结构强度和沙粒间的摩擦共同作用影响的结果。τB与泥石流浆体的浓度和流体内细颗粒和粗颗粒的含量有密切的关系。许多研究人员在实验研究和野外原型观测的基础上，总结出了许多较有代表性的经验公式(表1)。

表1 泥石流宾汉体结构应力公式Tab.1 Bingham yield stress formula of debris flow slurry

本文选用费祥俊［11］提出的泥石流浆体的结构力关系式

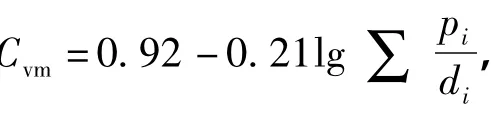
1.2.2 挟沙力公式 本研究以张瑞瑾等［14］公式为基础，推导出泥石流挟沙力公式

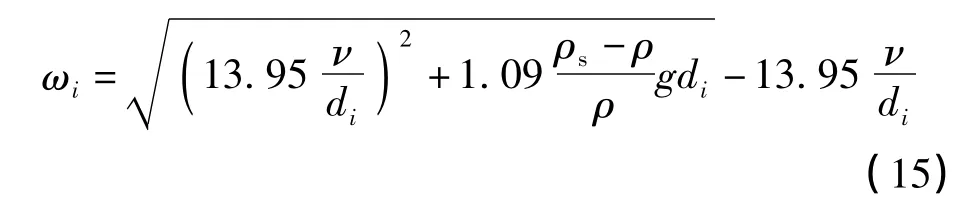
2 泥石流运动模型在云南蒋家沟的应用

2.1 研究区域概况

蒋家沟流域地处云南东川金沙江支流小江河谷右岸，是小江流域内泥石流活动频率最高的一条泥石流沟，流域面积48.6 km2，主沟长13.9 km。沟内岩性软弱、岩层松散、断裂纵横、地形陡峻、植被稀疏，地表形态破碎，滑坡和崩塌活动非常强烈，泥石流发生频繁。蒋家沟泥石流观测资料较多，系列较长，为从事相关理论研究提供了良好的基础［1］。

2.2 模型输入条件

模型计算范围选取蒋家沟中下游区域作为数学模型计算沟段，包括多照沟、门前沟沟口下游至入小江口，全长约5 km。根据蒋家沟DEM(10 m×10 m)进行网格划分，整个计算范围划分成56×35=1 960个网格。采用中国科学院东川泥石流观测站1975年5 月的1 次实测黏性泥石流运动过程作为上游输入的流量过程，模拟泥石流在沟道内的运动和冲淤过程。泥石流过程的含沙量、流量过程线如图1 所示。在蒋家沟泥石流主要补给区采集土样并分析颗粒物质组成，作为输入的泥石流泥沙颗粒级配，泥石流泥沙颗粒级配曲线如图2 所示。

图1 泥石流流量、含沙量过程线Fig.1 Changing process of discharge and sediment concentration of debris flow

图2 泥石流泥沙颗粒级配曲线Fig.2 Grain size distribution of the debris flow sample

2.3 泥石流运动过程的模拟结果

图3 是模拟的泥石流运动随时间的演进过程。由图可见，在泥石流开始运动时(t=0.1 h)速度较小，运动较缓慢，随后由于河床比降增大，流速增大，同时泥石流沿着沟道迅速展宽(t=0.5 h)，当泥石流流量达到峰值时(t=1.0 h)，泥石流在沟道中的流速也达到最大，并快速运动流出蒋家沟谷口，随后随着流量下降，泥石流流速也随之降低。模拟的运动过程和野外观测的泥石流实际运动规律基本吻合。

图3 泥石流运动过程模拟结果Fig.3 Simulated debris flow pattern

2.4 泥石流冲淤的模拟结果

图4 是模拟的泥石流在泥沙含量最大时(t=2.0 h)和整个过程结束时(t=3.6)沟道的冲淤状况。根据模拟结果，淤积和冲刷幅度与泥石流的流量、含沙量有密切关系。泥石流主要在沟口淤积，而且随着泥石流泥沙的沉积，沟口的淤积厚度不断增加。在泥石流运动过程中，由于沟床比降增大，泥石流流速增加，挟沙力增加，同时由于泥沙在沟道上游沉积，泥石流含沙量减小，因此下游沟道受到明显冲刷。模拟的泥石流淤积厚度一般为0 ～0.5 m，冲刷变幅一般为0 ～0.02 m，说明泥石流影响下蒋家沟下游沟道的基本上达到了冲淤平衡的状况，泥石流过程前后地形改变不大。冲淤模拟结果符合蒋家沟沟床泥石流冲淤演变的基本规律。

图4 泥石流冲淤模拟结果Fig.4 Simulated bed erosion-deposition depth

3 小结

结合水沙混合流模型和宾汉体模型理论建立了适于描述泥石流的二维非恒定两相流数值模型，避免考虑颗粒间的微观作用力，并从整体上保证模型具有较高的精度。

模型以云南东川蒋家沟为例，研究了泥石流运动随时间的演进过程，定量分析了泥石流冲淤影响下沟道形态的演变，模型模拟结果和野外实际观测到的泥石流运动及冲淤特征基本符合，证明该模型能够较客观地反映泥石流龙头随时间的动态变化过程和泥石流影响下沟道上下游不同区域的冲淤规律，这说明模型建立的机制正确，参数取值也基本合理。模型对于泥石流灾害预测和防治具有重要的现实意义。

［1］ 吴积善，田连权，康志成，等.泥石流及其综合治理［M］.北京: 科学出版社，1993:17-19

［2］ Johnson A M，Rahn P H.Mobilization of debris flows［J］.Zeitschrift fur Geomorphologie，1970，9(Sup):168-186

［3］ Takahashi T.Mechanical characteristics of debrisflow［J］.Journal of the Hydraulics Division，1978(104):1153-1169

［4］ Chen Chenglung.Generalized viscoplastic modeling of debris flow［J］.Journal of Hydraulic Engineering，1988，114(3):237-258

［5］ 王光谦，倪晋仁.泥石流动力学基本方程［J］.科学通报，1994，39(18):1700-1704

［6］ 余斌.二维定常泥流的数值模拟［J］.自然灾害学报，1995，4(4):96-99

［7］ Zhang Wanshun，Cui Peng，Qiao Fei.Numerical simulation of interaction between tributary debris flow and main river［J］.Journal of Sichuan University:Engineering Science Edition，2005(S1):75-80

［8］ 钱宁，王兆印.泥石流运动机理的初步探讨［J］.地理学报，1984，39(1):33-43

［9］ 费祥俊，朱平一.泥石流的粘性及其确定方法［J］.铁道工程学报，1986(2):9-16

［10］沈寿长，谢慎良.粘性泥石流的结构模式和流变特性［J］.铁道工程学报，1986(4):26-33

［11］费祥俊.黄河中下游含沙水流粘度的计算模型［J］.泥沙研究，1991(2):1-12

［12］王裕宜，詹钱登，邹仁元，等.泥石流浆体屈服应力综合表达式的研究［J］.自然灾害学报，1999，8(3):103-110

［13］王裕宜，詹钱登，韩文亮，等.粘性泥石流体的应力应变特性和流速参数的确定［J］.中国地质灾害与防治学报，2003，14(1):9-13

［14］Zhang Ruijin，Xie Jianheng.Sedimentation research in China: Systematic Selections［M］.Beijing: China Water and Power Press，1993:57-60