答疑解惑之图形变换与圆

　　一、图形的变换
　　
　　在学习的几种图形变换中。我们怎么确定图形是运用了哪种变换?
　　图形变换中我们主要接触了平移、旋转和轴对称这三种，在这三种变换过程中，不变的是图形的形状和大小，改变的仅仅是图形的位置，(1)要判断一个图形是否包含平移变换，首先要观察该图形是否包含平移所需的“基本图形”，然后再观察平移的方向或平移的距离，即平移的方式。操作方法为观察对应点所连的线段是否平行(或在同一条直线上)且相等，(2)判断一个图形是否包含旋转变换时，我们首先确定它的旋转中心和旋转角度，再观察图形上的每一点是否都绕旋转中心沿相同的方向旋转相等的角度，操作方法为观察各组对应点与旋转中心的连线的夹角是否相等，(3)判断一个图形是否包含轴对称变换时，关键是确定它的对称轴，即观察各组对应点连线段的垂直平分线是否重合为一条直线，
　　
　　成轴对称与轴对称图形是一回事吗?
　　不是，成轴对称与轴对称图形是两个极易混淆的概念，它们之间既有联系。又有区别，我们把一个图形沿着一条直线对折，如果能与另一个图形重合，则称这两个图形成轴对称，所以，成轴对称是指两个图形具有的特殊位置关系，而轴对称图形是指把一个图形沿着某一条直线折叠，直线两旁的部分能够完全重合，所以轴对称图形是指一个图形自身所具有的一种特殊形状，从定义不难看出，如果把成轴对称的两个图形看成一个整体，那么这个整体便是一个轴对称图形，而如果把轴对称图形位于对称轴两旁的部分看成两个个体，那么这两个个体就成轴对称，
　　
　　如何简便地找到成轴对称的图形的对称轴?
　　首先找到成轴对称的一组对应点，然后作该组对应点连线段的垂直平分线，这条垂直平分线即为所求的对称轴，对于有公共点且成轴对称的两个图形，由于它们的公共点在对称轴上，因此，只要作经过两个公共点的直线即可，
　　
　　怎样准确地判断一个图形是不是中心对称图形?
　　中心对称图形是指绕某一点旋转1800后能与自身重合的图形，所以判断一个图形是否为中心对称图形时，可先找旋转中心，观察图形是否包含旋转变换，然后观察各组对应点是否都关于同一点对称，即对应点的连线段是否都经过同一点，且被该点平分，如果上述两步都是肯定回答，那么该图形便是中心对称图形，
　　
　　一个正多边形旋转它一个内角的度数。旋转后的图形能与自身重合吗?
　　不一定重合，这种类型的题目很容易给同学们造成错觉，比如这样一个问题：等边三角形至少旋转多少度能与自身重合?很多同学容易错误地凭感觉得出600，其实，在分析一个图形旋转多少度后能与自身重合时，不能只看图形的表面已知量，而应该关注这个图形的旋转中心与一组旋转前后对应点连线的夹角，所以，解答上述例题时，不难发现等边三角形至少旋转的角度为360°÷3=120°其实，在所有的正多边形中，只有正方形旋转它一个内角的度数时，所得图形才能与自身重合，
　　
　　二、圆的性质及应用
　　
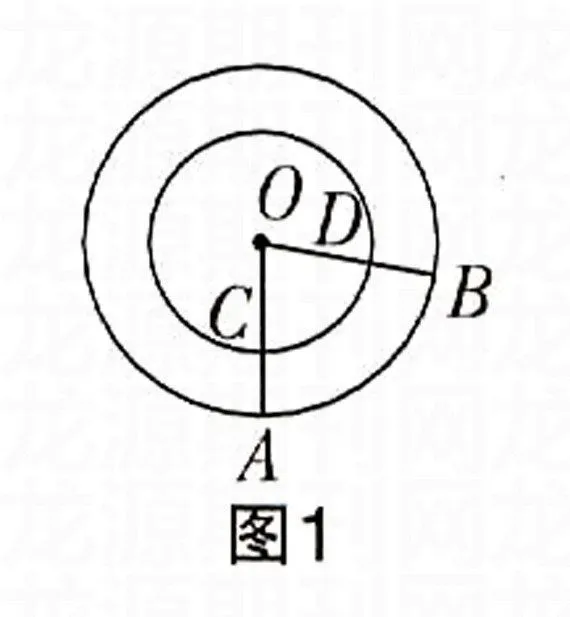
　　相等的圆心角所对的弧相等吗?所对的弦呢?不一定相等，若要相等需有一个重要的前提条件：在同圆或等圆中，如图1所示，在同心圆中，∠AOB与∠COD相等，但它们所对的弧与所对的弦显然不等，同理，若只具备两条弦相等，那么弦所对的弧、所对的圆心角也不一定相等，只有在同圆或等圆中。利用圆的中心对称性才能得出如下结论：如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等，
　　
　　
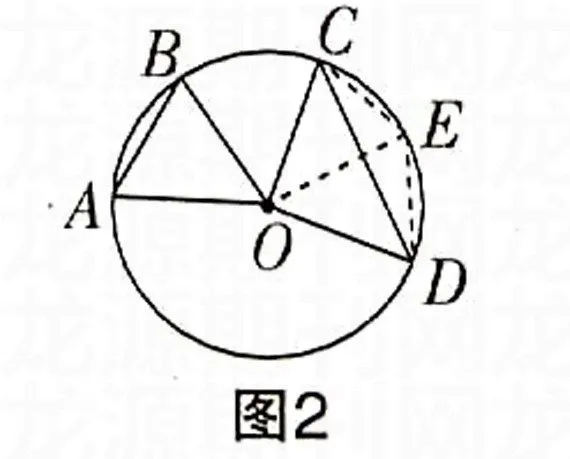
　　在同一个圆中。如果一条弧的弧长是另一条弧的弧长的2倍，那么这条弧所对弦的弦长也是另一条弧所对弦的弦长的2倍吗?
　　答案是否定的，在同一