中美小学数学计算教学比较

　　2011年上半年，笔者有幸参加了为期2个月的深圳市第15期赴美国圣文森山学院学习，在纽约市参观了近十所中小学，旁听了十多节小学数学课，收集了美国纽约州2套小学数学教材，对3所不同类型学校六年级100位学生及十多位成人进行了计算能力的问卷调查，对中美两国小学数学计算教学进行了比较。文中的中美两国小学数学教学主要是指中国广东与美国纽约州的小学数学教学。
　　一、从数学课程标准
　　及教材内容方面进行比较
　　1．课程标准方面
　　美国没有全国统一的数学课程标准，每个州制订本州的数学课程标准，各州的标准存在一定差异。整体而言，美国的数学课程标准涉及从幼儿园至高中数学内容：而我国数学课程标准分为义务教育数学课程标准及普通高中数学课程标准两部分，不涉及幼儿数学教育，国家也没有幼儿教育阶段的数学课程标准。本文重点以美国纽约州数学课程标准(New York State P-12 Common CoreLearningStandards for Mathematics)与中国义务教育数学课程标准小学部分内容进行比较。美国小学数学分成数与数的读写(Number and Numeration)、运算与估算(op—erations and Computation)、数据与概率(Data andChance)、几何(Geometry)、测量(Measurement and Ref—erence Frames)、规律(Patterns)、函数及代数(Functionsand Algebra)，中国小学数学分成数与代数、空间与图形、统计与概率、实践与综合应用四个部分。通过对比可以看出，中美两国小学数学均把数与代数作为小学数学的重点内容进行教学，只不过美国小学数学分得较细，把数与代数分成三部分，并把测量专门作为一部分进行教学，增加了“规律”部份，而“规律”是代数、函数的基础。
　　2．教材内容方面
　　在美国，不同的学校允许使用不同的教材，教材的选择权在学校。参考了几套教材发现，美国数学教材涉及知识面较广，有些知识的介入时间比中国教材更早，但难度深度不及中国教材，计算的难度也相对较低。比如分数教学，美国学生在小学一年级就开始学习简单的分数，分成四节课来学习，分别是：介绍平均分(Equal Parts)，要求学生数出平均分成多少份；学习分数1／2(One Half)；学习1／4(One fourth)；学习l／2、1／3、1／4(0ne Half OneThird and One Fourth)。通过多种活动来体会认识分数，比如动手为几何图形、常见事物的简笔画图形涂色。中国的教材中，都是教授了除法之后学习分数，除法是学习分数的基础，而美国的这套教材是把学习分数放在学习除法之前，把分数当成除法的基础。这一点与中国的数学教材差别很大。
　　美国的教材中出现了几节中国初中数学教材中的指数的内容，如10的幂、指数标记法、幂的正负、科学记数法，出现了指数及负数的简单运算，并介绍了运算顺序，再比如出现了正负数的简单运算，如负数的应用、正负数的加减法。学习数对之后还有两课时的初步认识坐标平面及两课时的一次函数的课程。美国计算教学中很重视平方数的教学，在问卷调查中，我们也发现学生、成人较善于利用平方数来进行计算，比如计算25×28时，有学生是这样计算的：25×25=625，25×3=75，625+75=700。显然，他利用了平方数进行计算，相比大多数中国人的计算方法来说比较独特。在对成人进行调查时也发现，对156+12这道题目，他们是这样运算的：12×12=144，144+12=156，得出结果13，使用了平方数进行计算。通过交流发现，他们已把20以内的平方数记在脑中。调查中发现，这种口算方法在美国较普遍，但在中国很少见。中国小学数学中的九九乘法口诀对学生帮助很大，学生熟背九九乘法表后，计算乘除法就会很轻松，而美国教材中没有出现过类似的口诀。
　　二、从学习环境，教学方式
　　方法方面进行比较
　　在学习环境方面，美国教师很注重教室环境的布置，他们会把一些最近学习的重要的数学知识、数学概念、公式等张贴在教室四周墙上，方便学生随时学习。教室通常分成以下几个功能区：一是学习区，主要供学生学习使用，配备了电子白板、黑板、电脑投影等教学设备；二是资料阅读区，相当于一个小型图书馆，为学生准备了学习时常用的资料、学具，并配备一两台电脑供学生上网查阅资料;三是游玩休息区。
　　在教学形式方面，在美国小学课堂上，学生通常以小组形式开展学习。每堂课至少有两位教师同时上课，一位为主讲教师，另一位为助教。每班学生人数不超过25人。主讲教师负责调控教学及安排学生的学习任务。主讲教师有时把学生集中起来讨论学习中遇到的问题，有时讲解重点内容，有时安排学生独立探究然后在小组内分享，有时是两位教师参与小组学习、讨论，学生还可以在教师的指引下操作学具，学习形式多种多样。美国课堂上，学生较自由，可以随便走动，但学生的走动必须是有目的的，或为了求助于教师或别的同学，或为了到资料区拿学具、学习资料，或为了喝水或上洗衣手间。由于各种原因，同一个班的学生在学习进度上存在区别，有的学生很快就能学会当天的任务，有的还存在一定困难。这时，两位教师会合理分工，一方面安排学习过关的同学到资料区，去研究新的更难一点的任务；同时会花更多的时间去关注那些学习上存在困难的学生，及时帮助辅导他们，有时是一对一的形式，有时是一对多的形式。
　　在教具与模型使用方面，在进行加减法计算教学时，中美教师使用的模型、学具也不相同。
　　例如：计算43-27=?的步骤如下。
　　
　　A．摆出43，见图1。B．减去20，见图2。C．3不够减7。借—当十，见图3。
　　
　　
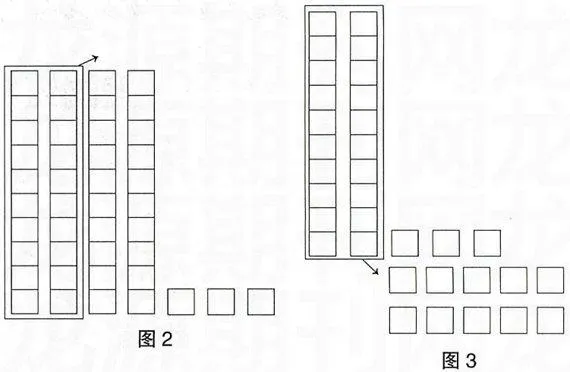
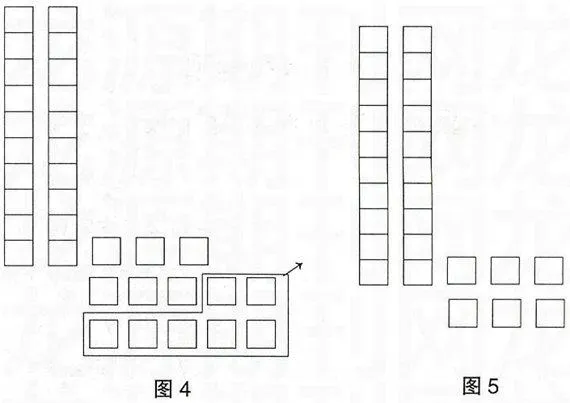
　　通过上述方法可以知道，美国教师是用一个小方块代表1个一，一条小方块(10个小方块)代表一个十，一块(10条小方块)代表一个百，来体现十进制原理，让学生理解数位，理解满十进一、借一当十的道理。我们中国教师的做法是，以一根小棒代表1个一，一捆小棒(10根)代表1个十。两种方法均能较好地化抽象为形象。但美国的这种模型除了适用于整数加减法，还能在小数加减计算中继续起作用，具有连贯性。中国北京师范大学版小学数学教材是以人民币为模型展开小数加减法计算，人民币的计算对学生来说是生活中常遇到的事情，更具情景性、趣味性及实用性。
　　下面展示美国小数计算时的模型，以2.34＋1．27=?为例，见图6。
　　
　　三、从算法与算法优化方面进行比较
　　中美小学计算教学都注重学生口算能力的训练，都强化了估算教学，都注重算法多样化与算法优化的整合，但也存在一些不同的地方。
　　1．中美计算教学均提倡算法多样化，但美国的算法非常有个性
　　大部分美国学生在进行乘法计算时用竖式计算，但也有一些相对中国人而言非常独特的、个性化的计算方法。
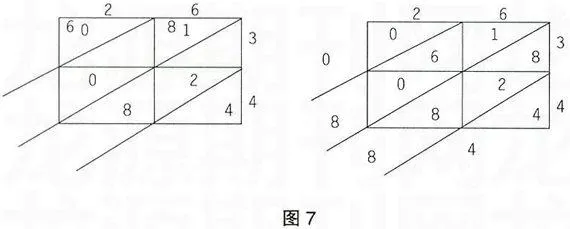
　　例如：计算34×26=?时，有学生采用了格子方法，为了方便研究，我把计算过程分成如下图两步，得出结果34×26=884，见，图7。
　　
　　再比如计算26×5=?时，有学生使用竖式方法计算，但与我国的计算方法区别很大。他们是先用5乘以乘数26之中十位上的2，再乘个位上的6，最后把两个积加起来(见图8)。
　　中国乘法计算是要求先乘个位，再乘十位，最后把两层积加起来。在中国，如果学生出现这种先算十位再算个位的情况，教师通常会认为方法错误，纠正后引导到先算个位再算十位的方法上来。美国的教师则完全认可学生的这种计算方法。
　　再比如，美国教师在教学除法计算时，学生也出现了非常有个性的计算方法。
　　如：计算371+4=?，见图9。
　　
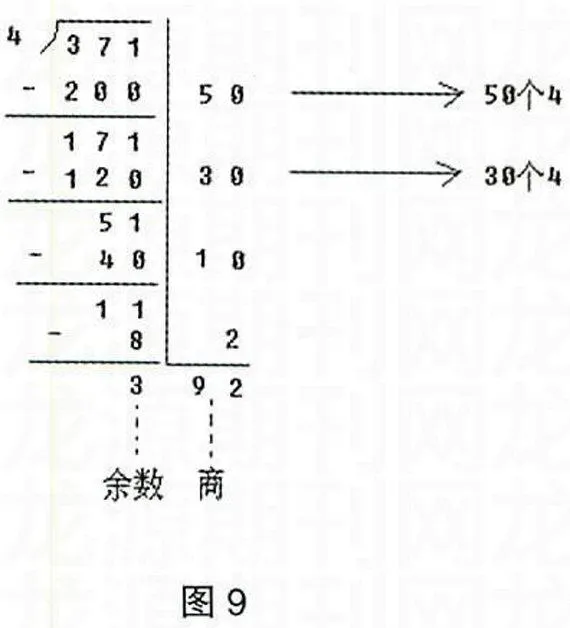
　　这种方法允许学生得到的余数大于除数，余数大于除数时，继续除，直到不能除为止；然后把每一步的商加起来就是最后的结果，这种方法对学生的试商能力要求不高，对于学数学存在困难的同学帮助很大。中国除法竖式计算通常只有一种方法，计算时绝对不允许出现余数大于或等于除数的情况。
　　再比如，在美国二年级两位数加减法教学时，计算：27+16=?时，美国教师还允许学生借助表格工具进行计算(见图10)。而我们在教二年级计算时，通常要求学生不能再借助手指或其他工具去计算，必须去思考，或列竖式笔算。
　　
　　可以说，中美在计算教学均注重算法多样化，但通过观察可以看出，美国学生的计算方法更有个性，美国教师也很尊重学生的个性发展。
　　2在算法优化方面，中国教师倾向于统—算法，美国教师更尊重个性化算法
　　在教授计算新课程时，中国教师也非常重视算法多样化，但到了优化阶段，教师通常会选择自认为的最快最好的一种计算方法，接着通过让学生大量练习来强化这种方法。在这种模式下，其他的计算方法就被否决了，学生最后只能掌握一种方法。但学生之间存在差异，思维不同，基础也不同，我们认为最好的方法可能未必适合一些学生。在这种模式的长期影响下，有创造思维的学生也不会再尝试自己的方法。美国教师非常尊重学生的差异，鼓励学生尝试不同的方法、寻找适合自己的计算方法，不强迫孩子使用教师认为最高效、最好的方法。学生们的个性化算法因此得到保持。
　　对于25×28=?，没有一位学生使用了把28分成7乘4，再利用4乘25等于100的简便方法进行计算。原以为美国孩子也会像中国孩子一样，看到25马上就会联想到4，这点大大出乎我的意料。这也可看出中美计算思路的差别性。调查后，我把这种方法对他们进行介绍，学生很感兴趣。
　　四、从作业要求、书写要求方面进行比较
　　可以说中美学生作业要求差别很大，美国教师对学生的书写要求不如中国教师严格。大部分美国学生数学作业书写比较潦草，教师对学生作业的书写要求也较低，允许六年级学生使用铅笔答题。中国数学教师对于计算书写有一套严格要求，比如列竖式时，数位要对齐，横线需用尺子画，等号要写得一样长，不允许一长一短。再比如书写多步计算题(梯等式)时，中国数学教师通常要求学生将等号对齐，过程需一步一步写清楚。中国教师通常要求三年级以上的学生不能再用铅笔答题。
　　然而美国教材中也经常会出现一些不够规范的现象，比如多步计算没有等号等情况。如美国小学数学四年级教材(Everyday Mathematics)中，第151页的梯等式就没有等号。虽然例题主要目的是介绍运算顺序，但可以看出教材的示范性不如中国教材。美国学生看到教材上没有等号，会以为不写等号是可以的。所以，调查中的美国成人、学生的多步计算书写出现类似情况也就理所当然。
　　五、从运算符号的使用方面进行比较
　　美国数学深受计算机文化影响，融合了计算机语言的一些文化，比如使用3／4表示3÷4。再比如乘号可以用“*”表示，教材中也有提及到并且允许使用。目前中国教材中还没有涉及到这些符号，没有提及允许使用这些符号。这一现象在一定程度上反应出美国文化的包容性。
　　六、从评价与测试方面进行比较
　　美国各州从小学三年级开始有各州举行的统一考试，学生成绩分成A、B、C、D、E五个等级，各学校各等级的人数比例会公布在州教育部网上，统考成绩与学校的办学绩效挂钩，教育部门不仅看各学校当年的成绩，而且会与学校往年的成绩进行对比。
　　笔者对三所学校的六年级学生进行了计算能力的问卷调查，问卷以两步计算为主，最后附上一个问题“你是否喜欢学数学?”。笔者曾用这套问卷对广东省深圳市宝安区实验学校六年级学生进行了调查。出于公平的原则，在美国的测试选择六年级的学生(美国的六年级属于中学)。计算能力统计结果如下：美国学生达A(i00分)的占41％，B(80-99分)的占30％，C(60-79分)的占20％，D及E占9％。中国学生达A(100分)的占78％，B(80-99分)的占20％，C(60-79分)的占2％，D及E占O％。可以看出，中国学生的计算能力(计算正确率)比美国学生强，中国学生的书写也比美国学生工整。但对最后一个问题“你是否喜欢学数学?”，有55％的美国学生表示喜欢学数学，有56％中国的学生也表示喜欢学数学，比例接近。虽然中国学生的计算能力远远高于美国学生，但真正喜欢学数学的学生人数比例并没有随成绩优秀而高一些，这一点也值得我们深思。
　　七、从使用计算器方面进行比较
　　美国教材中花了大量课时介绍计算器，学生从一二年级就开始按触计算器，教材专门用1个单元7页篇幅介绍普通计算器的使用，小学毕业班教材还专门用1个单元6节36页篇幅介绍数学计算器的使用。在中国，中低年级学生是绝对不允许使用计算器的，高年级学生也不例外，考试时学生也只能笔算，不能使用计算器。中国的考试目前也删除了一些繁杂的计算，但仍然要求学生考试时不能使用计算器。另外，在美国，每册数学教材均附上了许多数学游戏方法，供教师参考和使用。
　　八、结语
　　综上所述，中美两国均很重视计算教学，均使用一些模型或学具帮助学生理解计算原理，都意识到口算、估算及算法多样性的重要性。中美教师在小学数学计算教学方面各有优劣，美国教师较尊重学生的个性，注重学生个性发展；中国教师更注重效率，对学生的书写、计算格式更严格。对比中也发现，美国学生个性发展较好，创造性思维发展较好；中国学生计算技能、计算能力较强，计算正确率高，书写普遍较工整。由于笔者所调查与研究的对象主要以纽约州部分学校、学生为例，具有一定的局限性，难以推及美国国家层面。但这些点滴现象对于今后的教学，特别在如何培养学生的创造性思维方面，仍能起到一定的借鉴参考作用。
　　参考资料：
　　[1]New York State P-12 Common Core Learning Stan-dards for Mathematics[EB／OL].http：／／www.p12.nysed.gov／ciai／common_core_standards／pdfdocs／p 12 common core learn-Lug.standards mathematics final ．pdf2011-6-1．
　　[2]Everyday Mathematics frhe University of chicagoSchooI Mathematics Project)[M]．New York：McGraw HillWright Gr