畸形波生成、演化过程研究——波面时间过程随位置的变化

崔成，张宁川，裴玉国

（大连理工大学 港口海岸及近海工程国家重点实验室，辽宁 大连 116024）

畸形波生成、演化过程研究
——波面时间过程随位置的变化

崔成，张宁川，裴玉国

（大连理工大学 港口海岸及近海工程国家重点实验室，辽宁 大连 116024）

基于完全非线性波浪数值模型，模拟实测畸形波的生成、演化过程，进而分析波面时间过程和畸形波参数的变化规律。研究结果表明：在畸形波形成前、后均可能出现连续的大波和“深谷”现象。在畸形波生成、演化过程中出现的“深谷”和畸形波具有伴生性而非独立异常波浪现象。上述大波、“深谷”和畸形波的连续作用对海洋结构物和船舶造成的潜在威胁可能远超过“瞬态”畸形波，此点应引起高度重视。

畸形波；生成、演化过程；深谷

已有一定量关于畸形波的研究和探讨，但是关于畸形波形成、演化过程的研究还相对较少。Osborne[1]等根据 B-F不稳定性使用非线性薛定谔方程模拟了畸形波的发展过程，并指出在巨大波峰前后都会形成深谷。Stansell[2]分析北海实测记录时，给出了实测记录中包含深谷的时间序列，其中波谷5.38 m，有效波高3.79 m，波谷与有效波高的比值1.4。Clauss[3,4]指出，在恶劣的海况条件下，不仅发生独立的大波还会发生汹涌的大波群，并通过物理实验和数值水槽分别模拟了上述两种极端波浪。

现有理论研究和实测资料均间接表明，在畸形波形成和演化过程中，可能接连出现波高略小于畸形波的的连续大波和巨大深谷。由于他们一起对海洋结构物和船舶造成巨大的潜在威胁可能远超过“瞬态”畸形波，因此有必要对畸形波生成、演化过程进行进一步深入研究和探讨。

本文采用完全非线性数值模型模拟畸形波生成、演化过程，分析畸形波和连续大波、深谷之间的伴生关系。

1 畸形波模拟的非线性数值模型

将二维不可压缩流体的连续方程和完全非线性N-S方程作为畸形波模拟的非线性数值模型的控制方程，设定恰当的数值水槽边界条件，基于VOF方法求解，获得含有畸形波的波动过程。

1.1 控制方程

采用 VOF数值方法时，不可压二维流体的连续方程可记为：

式中 u，v分别表示 x，y方向的速度分量；gx，gy分别表示x，y方向的体积加速度；p为流体压力；ρ为流体的密度；ν为流体的运动粘滞系数。

1.2 边界条件

1.2.1 自由表面条件 波浪自由表面可以根据体积函数分布计算得到。体积函数F满足下面的控制方程：

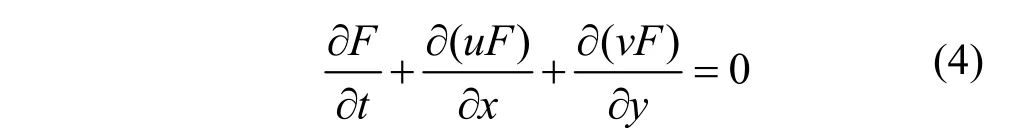
1.2.2 数值水槽造波边界 在此考虑了两种情况：①模拟实测畸形波序列（新年波，北海畸形波，北海深谷）的生成、演化过程时，数值水槽造波边界采用单波列叠加模型；②人工数值生成畸形波序列时，数值水槽造波边界采用双波列叠加模型。

单波列叠加模型的波面可描述为：

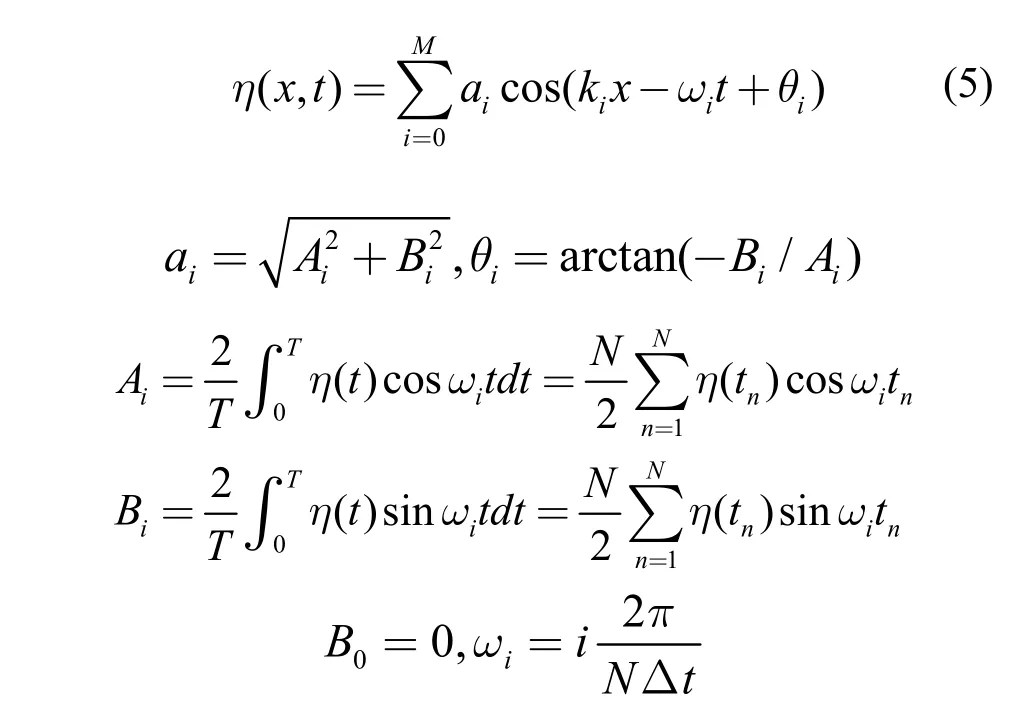
N是样本个数，∆t为采样间距，i表示组成波编号i = 0，1，2，……， M；M表示组成波个数。

双波列叠加模型的波面可描述为：

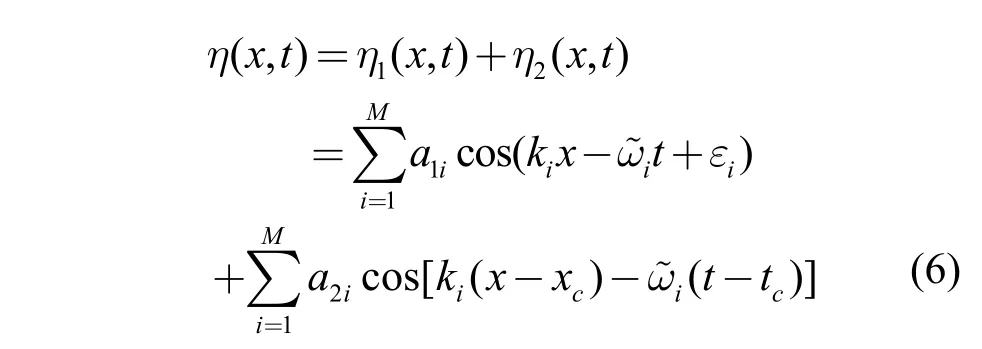
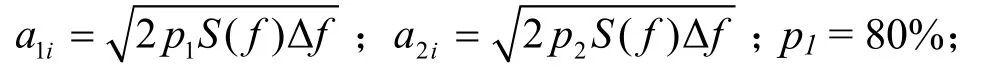
根据造波理论，造波边界处的水平速度 U0(t)的表达见式(7)

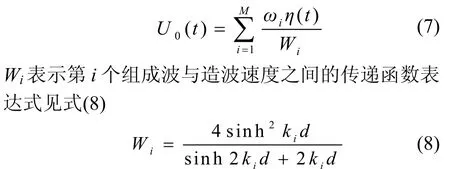
1.2.3 数值水槽吸收边界 数值造波水槽远端边界采用的是海绵层边界。二次反射的吸收采用了主动吸收的方法[7]。

1.2.4 数值水槽水底边界 数值水槽水底为平底，边界条件为：Uy(i, 1) = 0，Ux(i, 1) = Ux(i, 2)。其中Uy(i, 1)表示水底层网格垂向速度分量，Ux(i, 1)和Ux(i, 2)分别表示水底层及其上一层网格水平速度分量。

2 数值水槽的有效性验证

2.1 数值波浪水槽有效性验证

水槽长为6 000 cm，划分1 200×30个网格，网格尺寸5 cm×3 cm，时间步长0.02 s，计算时间150 s，采集点距造波板2 002.5 cm处（满足大于6倍谱峰周期对应的波长,目标谱选用修正 PM 谱（ITTC，1972）。表达式见式(9)～(11)。

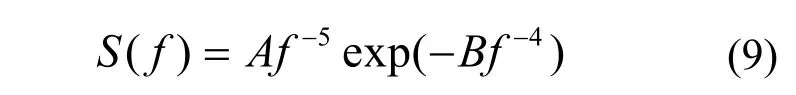
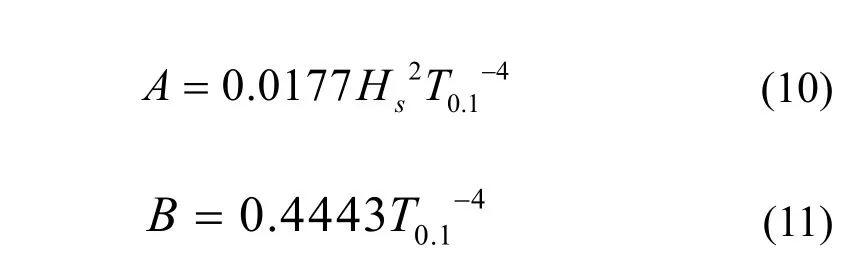
图1给出了数值水槽的布置图。为了验证本文所建立的数值模型有效性，使用该模型模拟一组条件为水深d = 50 cm；Hs= 5.00 cm和Tp= 1.50 s的不规则波列。模拟结果有效波高和谱峰周期分别为Hs=5.08 cm和Tp= 1.54 s。图2给出了数值计算的波面时间过程及其傅里叶能量谱和目标波面及谱的比较，对比发现两者计算结果基本吻合，可见本文所建立的数值水槽对不规则波浪的模拟具有一定的有效性。

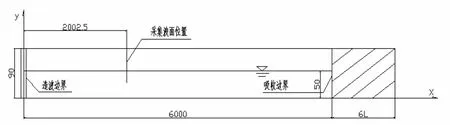
图1 数值水槽示布置（单位：cm）Fig. 1 Sketch of the computation domain (unit： cm)

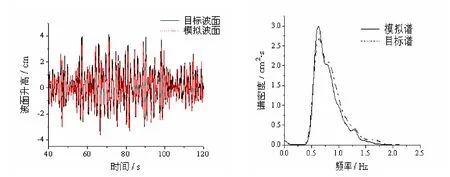
图2 数值计算波面及傅里叶谱与目标波面及傅里叶谱的对比Fig. 2 Comparison of target wave surface elevation and computed wave surface elevation (left) as well as comparison of target spectrum and computed spectrum (right)

再使用该模型模拟在d = 50 cm；Hs= 6 cm和Tp= 2.5 s条件下模拟一组包含畸形波的不规则波列。图3给出模拟结果，该畸形波参数为：Hs= 6.05 cm，Hj=15.51 cm， ηj=10.36 cm，α1=2.52，α2= 2.08，α3= 3.90，α4= 0.67。其中Hs表示波列有效波高，Hj表示畸形波波高，ηj表示畸形波波峰，α1表示畸形波波高与有效波高的比，α2表示畸形波波高与前一个相邻波高的比，α3表示畸形波波高与后一个相邻波高的比，α4表示畸形波波峰与畸形波波高的比。

以上 2算例表明本模型不但可以有效地模拟常规不规则波列，还可以模拟包含畸形波的不规则波列。

3 畸形波生成、演化过程

作为具有代表性的算例，在前面提到的数值水槽中，定点模拟目标波面为天然条件下实测得到的三组波面时间过程（新年波，北海畸形波，北海深谷[2,5]）和 4组人造畸形波，进而分别讨论上述 7组不同畸形波波面的生成、演化过程。

在数值水槽中，指定在距离造波边界大于6倍有效波长处生成目标波面。计算波面生成、演化过程时，考察了畸形波生成位置前后各 4～6倍有效波长范围内，100倍平均周期时段内波面变化。波面空间采样间隔5 cm；时间采样间隔0. 02 s。

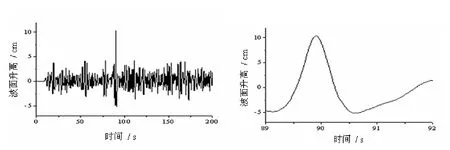
图3 模拟畸形波Fig. 3 Simulated freak wave

3.1 实测天然畸形波的生成、演化过程

3.1.1 实测新年波的生成、演化过程 表1详细给出了实测[2]和模拟新年波相关参数值的比较。其中的T表示平均周期，L表示平均波长，T2= 2πL / (g th2πd / L)，图4给出实测和模拟的新年波波面时间过程比较。表1和图4的结果显示，新年波模拟结果与实测值吻合良好。

指定新年波（畸形波）在X=1 992.5 cm（距离造波板7倍有效波长）处生成。图2分别给出了畸形波生成位置前后各4倍有效波长范围内、8个代表点处、采集的 30倍谱峰周期时段内波面时间变化过程。

其中8个代表点的选取原则为该点波面时间过程含有满足畸形波定义参数的较大波浪。将波面时间过程进行 T*= (t – tc) / Tp，η*= η / Hs无量纲和时间归零处理，较大波高出现在T*=0时刻。

图5(a) ～ (d)分别给出了畸形波生成位置前4倍有效波长范围内、4个代表点处、采集的30倍谱峰周期时段内波面时间变化过程。4个代表点为X =1 492.5 cm、1 727.5 cm、1 927.5 cm和1 992.5 cm，距离畸形波的生成位置分别为：-1.7、-0.9、-0.2和0倍有效波长（-表示畸形波生成前）。在该4组序列中，分别出现满足α1= 2.16的波浪（α1＞ 2，仅能满足畸形波定义的第一个参数，该波浪与邻近的波浪一起表现为连续的大波），满足α1= 2.18和α2=2.18 的波浪（α1＞ 2 和 α2＞ 2 满足畸形波定义的第一和第二个参数，该波浪的波谷很大，形成了深谷），满足 α1= 2.13，α3= 2.73和 α4= 0.69的波浪（α1＞2，α3＞2和α4＞0.65满足畸形波定义的第一、第三和第四个参数，该波浪表现为波峰值较大的大波）和满足 α1= 2.21，α2= 2.18，α3= 3.66和 α4= 0.72的畸形波（α1＞2，α2＞2，α3＞2 和 α4＞0.65 满足畸形波定义所有参数）。

上述即为畸形波生成过程，可综合描述为：畸形波生成前，将首先出现连续大波（大波群），该波群继而形成较大的波谷，再生成畸形波。

图5(e) ～ (h)分别给出了畸形波生成位置后4倍有效波长范围内、4个代表点处、采集的30倍谱峰周期时段内波面时间变化过程。4个代表点为X =2 102.5 cm、2 157.5 cm、2 247.5 cm和2 397.5 cm，距离畸形波的生成位置分别为：0.4、0.6、0.9和1.4倍有效波长。在该 4组序列中，分别出现满足α1=2.26，α2=2.71 和 α3= 2.44 的波浪（α1＞2，α2＞2和 α3＞2满足畸形波定义的第一、第二和第三个参数，该波浪表现为独立的大波），满足 α1=2.11和α2=2.43 的波浪（α1＞2和 α2＞2满足畸形波定义的第一和第二个参数，该波浪的波谷很大，形成了深谷），满足 α1=2.14，α3=2.18 和 α4=0.65 的波浪（α1＞2，α3＞2和α4＞0.65满足畸形波定义的第一，第三和第四个参数，该波浪表现为波峰值较大的大波）和满足α1=2.00的波浪（α1＞2满足畸形波定义的第一个参数，该波浪与邻近的波浪一起表现为连续的大波）。

上述即为畸形波演化过程，可综合描述为：畸形波生成后，将首先演化为独立的大波（不同时满足畸形波定义的所有参数），然后出现较大的波谷，再演化成大波群，直至恢复到常规波浪形态。

表2给出生成、演化过程中出现的较大波浪的畸形波参数。本算例的畸形波生成、演化过程可简记为：连续大波→深谷→大峰值波→畸形波→独立大波→深谷→大峰值波→连续大波。空间范围约3.1倍有效波长，时间长度约10倍平均周期。

表1 实测和模拟新年波相关参数值比较汇总Tab. 1 Coefficient values for the simulated and measured New Year wave records

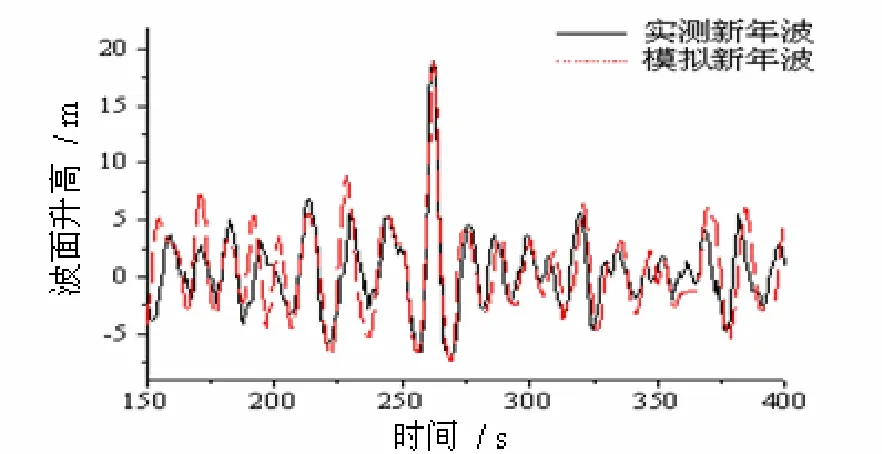
图4 实测和模拟的新年波时间过程Fig. 4 Measured and simulated New Year wave

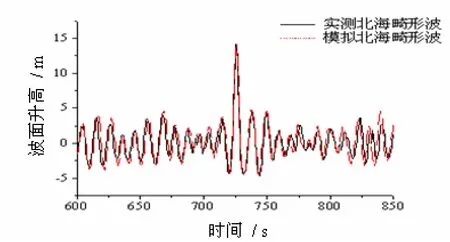
图 6 实测和模拟北海畸形波时间过程 Fig. 6 Measured and simulated North Sea freak wave

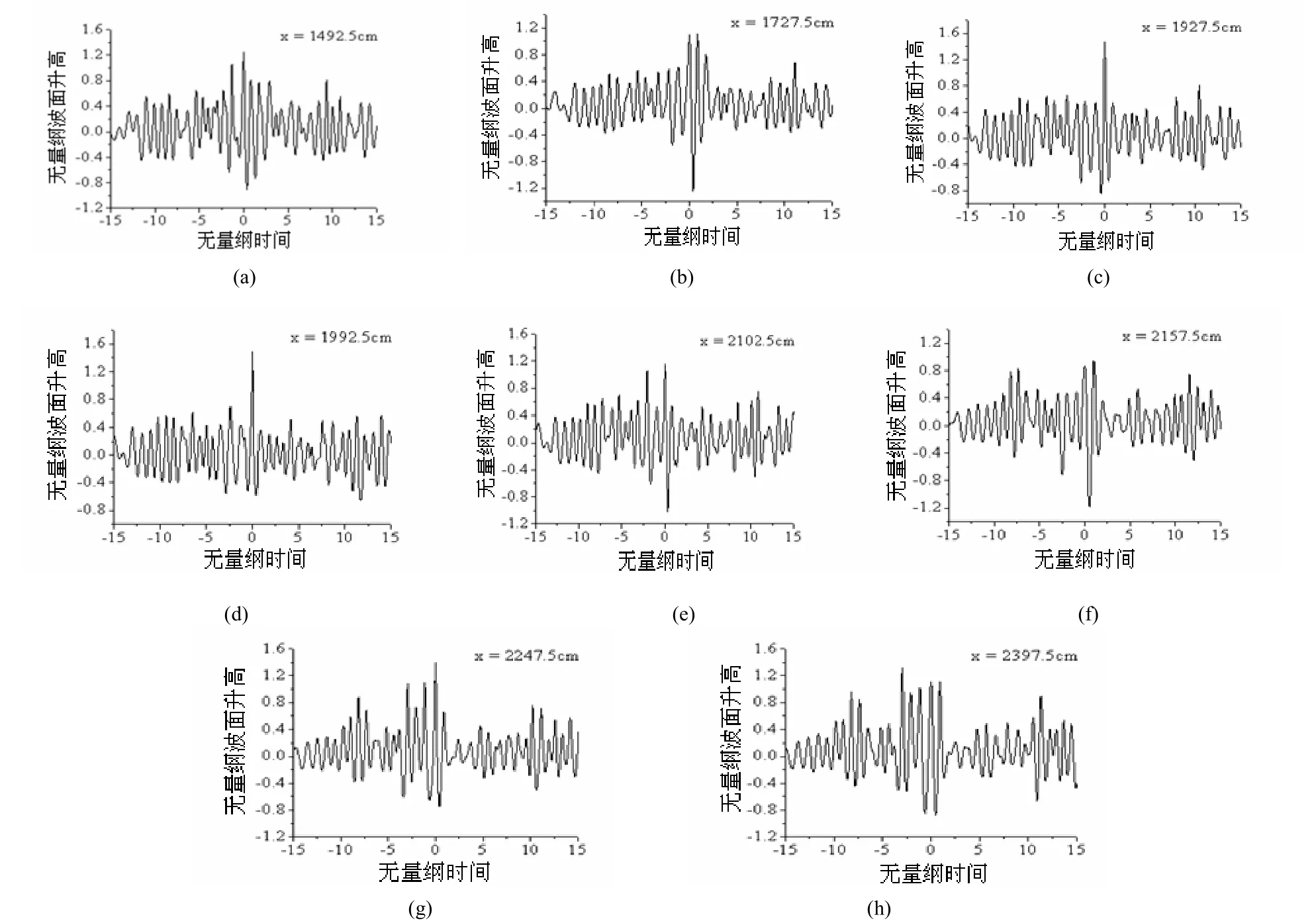
图5 新年波生成、演化过程中不同代表点波面时间过程Fig. 5 Time-process of water-surface elevation at different representative positions

3.1.2 实测北海畸形波的生成、演化过程 图 6给出实测和模拟的北海畸形波波面时间过程，表 3汇总给出了实测和模拟的北海畸形波参数比较。表3和图6的结果显示，北海畸形波模拟结果与实测值吻合良好。

指定北海畸形波在X = 1 962.5 cm（距离造波板约10倍有效波长）处生成。图7(a)～(g)分别给出了畸形波生成位置前后各 4倍有效波长范围内、7个代表点处、采集的30倍谱峰周期时段内波面时间变化过程。7个代表点为X = 1 663.5 cm、1 748.5 cm、1 930.5 cm、1 962.5 cm、2 037.5 cm、2 107.5 cm、2 231.5 cm，距离畸形波的生成位置分别为：-1.5、-1.1、-0.2、0、0.4、0.7、1.4倍有效波长（-表示畸形波生成前，+表示畸形波生成后）。表4汇总给出了北海畸形波的生成、演化过程中较大波的畸形波参数。

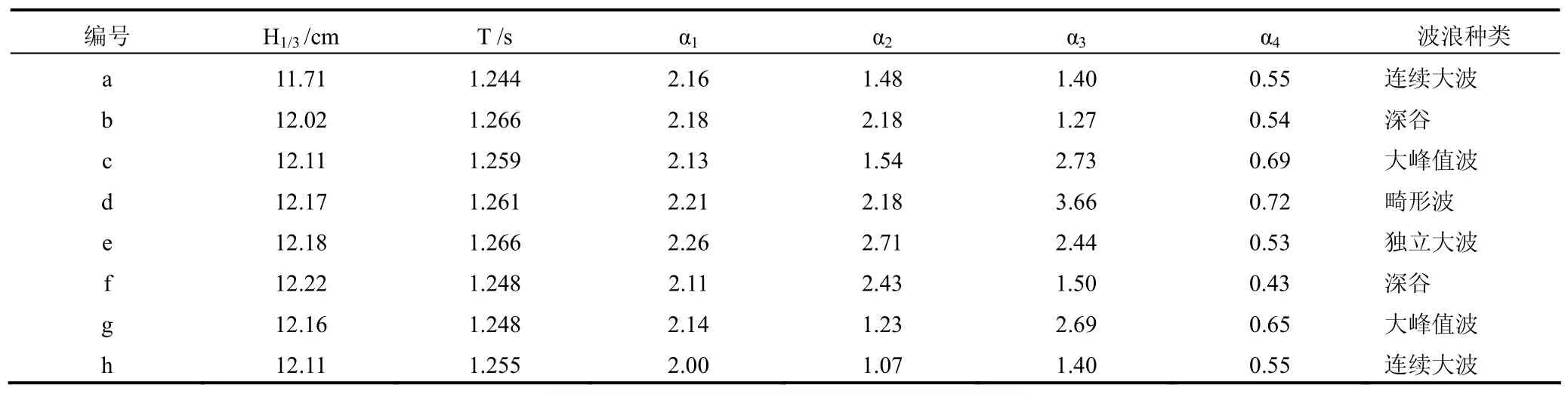
表2 新年波生成、演化过程中出现的极端波浪的相关参数值Tab. 2 Coefficient values for the extreme waves

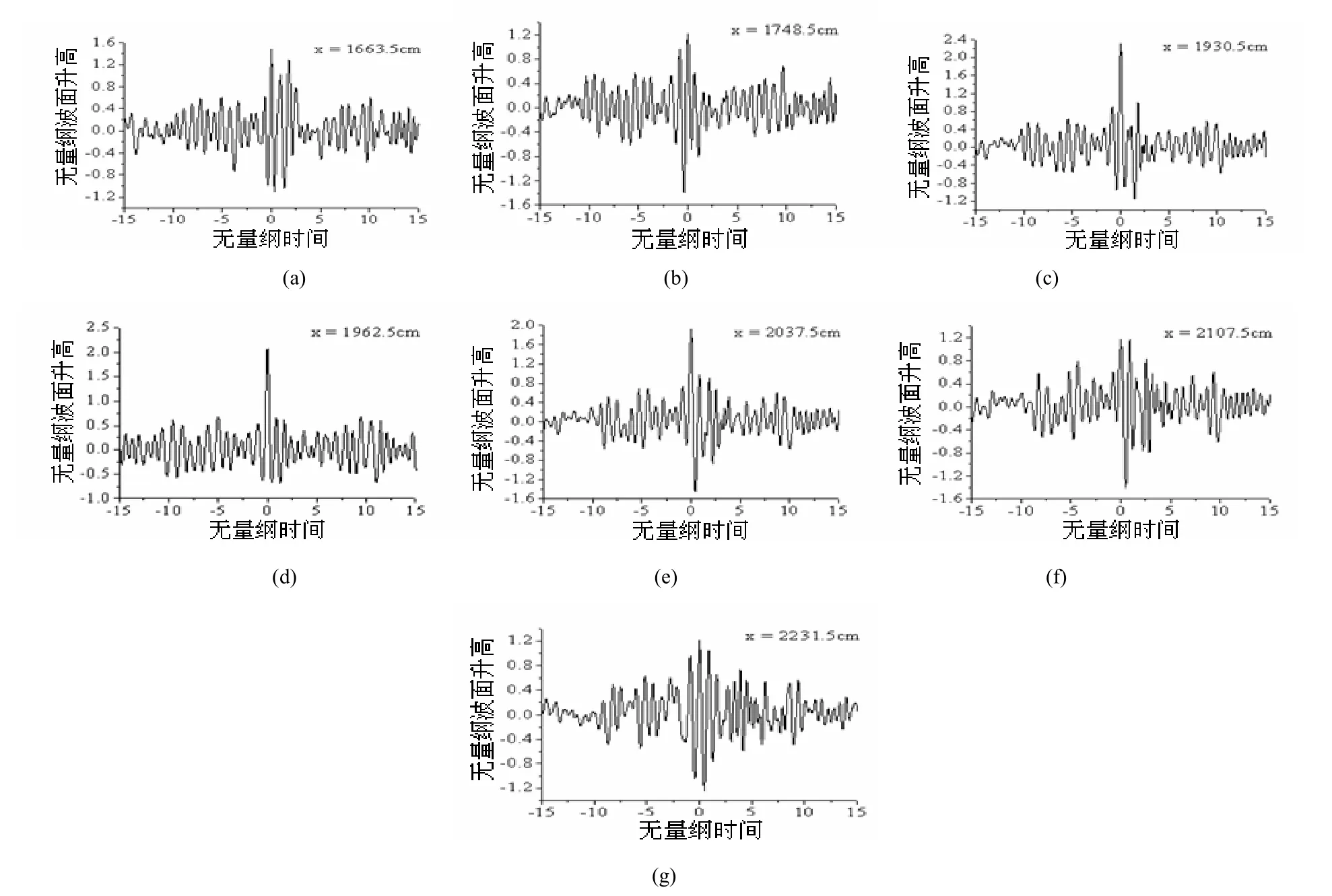
图7 北海畸形波生成、演化过程中不同代表点波面时间过程Fig.7 Time-process of water-surface elevation at different representative positions

表3 实测和模拟北海畸形波相关参数值比较汇总Tab. 3 Coefficient values for the simulated and measured North Sea freak wave records

表4 北海畸形波生成、演化过程中出现的极端波浪的相关参数值Tab. 4 Coefficient values for the extreme waves

综合比较实测北海畸形波与新年波的生成、演化过程，两者完全类似（与新年波的生成、演化过程的不同之处为：畸形波演化过程中不包含满足条件 α1＞2，α3＞2 和 α4＞0.65 的大峰值波），不赘述。空间范围约3倍有效波长，时间长度约9倍平均周期。

3.1.3 实测北海深谷的生成、演化过程 图8给出实测和模拟的北海深谷波面时间过程。表5汇总给出了实测和模拟的北海深谷参数比较。

表5和图8的结果显示，北海深谷模拟结果与实测值吻合良好。

指定北海深谷在X = 1 710.5 cm（距离造波板约9倍有效波长）处生成。图9(a)～(g)分别给出了深谷生成位置前后各6倍有效波长范围内、7个代表点处、采集的 30倍谱峰周期时段内波面时间变化过程。在X = 2 425.5 cm的位置采集到波面时间过程中包含畸形波。

7个代表点分别为X = 1 410.5 cm、1 710.5 cm、1 895.5 cm、2 425.5 cm、2 765.5 cm、2 835.5 cm、2 925.5 cm，距离畸形波生成位置分别为-4.6、-3.3、-2.4、0、 1.5、1.9、2.3倍有效波长（-表示畸形波生成前，+表示畸形波生成后）。表6汇总给出了与北海深谷相伴发生的畸形波的生成、演化过程中较大波的畸形波参数。

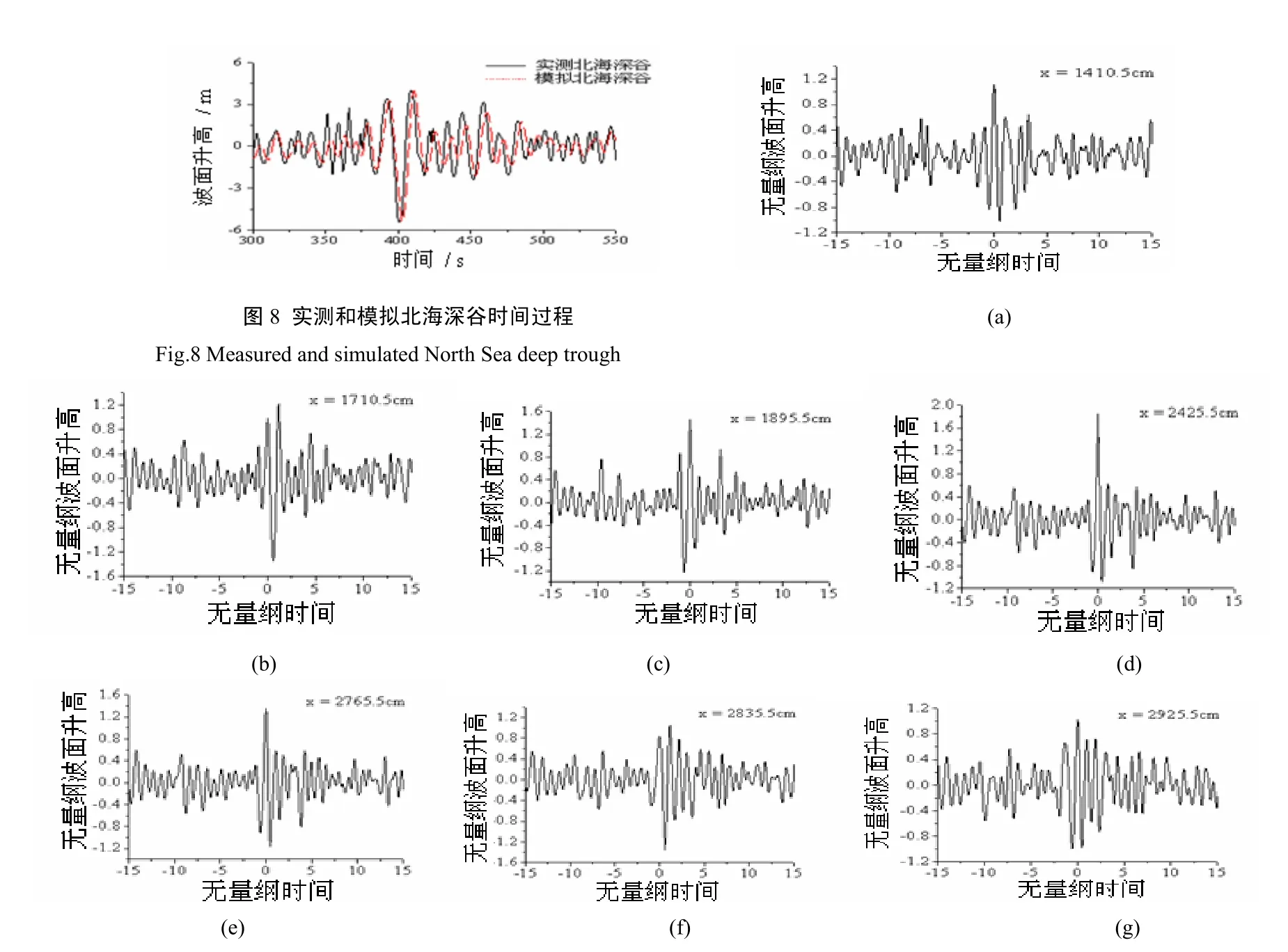
图9 北海深谷伴生畸形波的生成、演化过程中不同代表点波面时间过程Fig. 9 Time-process of water-surface elevation at different representative positions

表5 实测和模拟北海深谷相关参数值比较汇总Tab 5 Coefficient values for the simulated and measured North Sea deep trough records

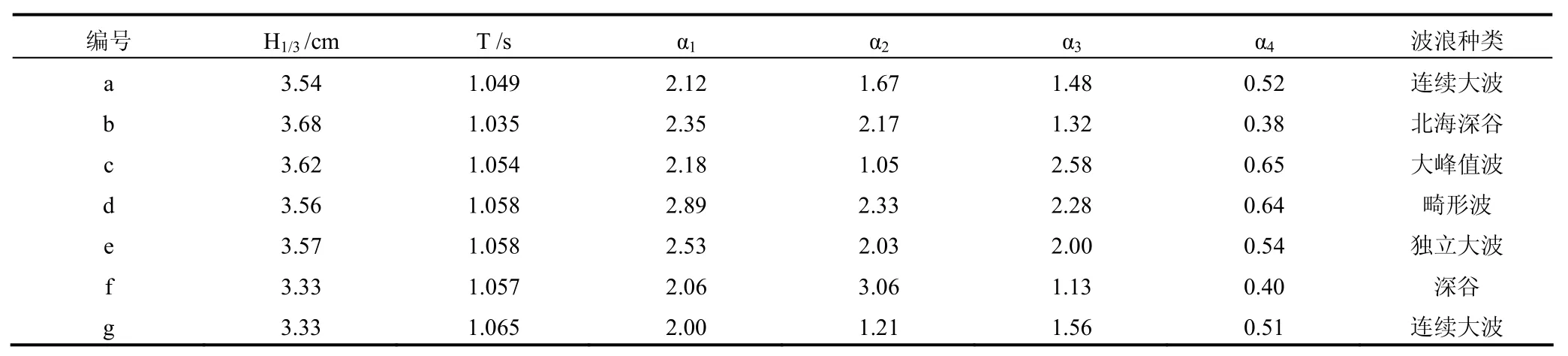
表6 与北海深谷伴生畸形波的生成、演化过程中出现的极端波浪的相关参数值Tab 6 Coefficient values for the extreme waves

综合比较该畸形波与前两组畸形波的生成、演化过程完全类似（与新年波的生成、演化过程的不同之处为：畸形波演化过程中不包含满足条件α1＞2，α3＞2和 α4＞0.65大峰值波），不赘述。空间范围约7倍有效波长，时间长度约13倍平均周期。

上述3个算例综合比较可以看出：

（1） 在畸形波生成过程中，首先出现不完全满足畸形波全部定义的较大波浪或连续的大波；进而出现波谷较大的波浪（通常称深谷），逐渐发展会形成满足全部定义的畸形波（满足α1＞2，α2＞2，α3＞2 和 α4＞0.65）。

（2） 畸形波演化过程中，首先会演化为独立大波，再演化为深谷，最终分化成连续大波。

（3）深谷与畸形波生成、演化过程有伴生性，而非独立出现的异常波浪。

表7汇总给出了伴随畸形波的生成、演化过程中无量纲深谷。（α5= ηtmax/ Hs，α51表示发生在畸形波之前无量纲波谷，α52表示发生在畸形波之后无量纲波谷）。比较可见，发生在畸形波生成、演化过程中的两次深谷最大值基本相同。

表7 深谷相关参数Tab 7 Coefficient values for the deep troughs

3.2 人造畸形波的生成、演化过程

模拟4组人造畸形波，对应的无量纲水深d / L分别为0.15，0.28，0.65，0.82。采用双波列叠加模型做为数值水槽的造波边界 ，4组人造畸形波造波条件分别为：（1）Hs= 5.2 cm，Tp= 1.8 s，d = 50 cm；（2）Hs= 4.2 cm，Tp= 1.0 s，d = 50 cm；（3）Hs=4.0 cm，Tp= 0.95 s，d = 80 cm；（4）Hs= 4.5 cm，Tp= 1.2 s，d = 150 cm。

在无量纲水深d / L = 0.15 条件下，指定畸形波在X=2515.5 cm（距离造波板7倍有效波长）处生成。图7(a)～(i)分别给出了畸形波生成位置前后各4倍有效波长范围内、9个代表点处、采集的30倍谱峰周期时段内波面时间变化过程。9个代表点分别为X=1 590.5 cm、1 940.5 cm、2 005.5 cm、2 515.5 cm、2 785.5 cm、3 005.5 cm、3 315.5 cm、3 510.5 cm和3 810.5 cm距离畸形波生成位置分别为-2.6、-1.6、-1.4、0、+0.8、+1.4、+2.2、+2.8和+3.6倍有效波长（-表示畸形波生成前，+表示畸形波生成后）。表8汇总给出了无量纲水深d / L = 0.15条件下人造畸形波的生成、演化过程中较大波的畸形波参数。

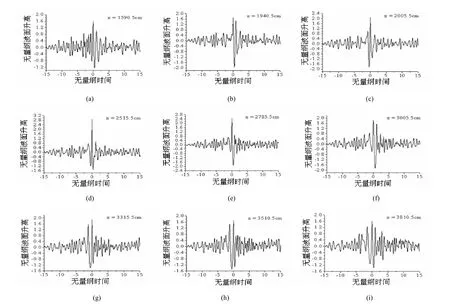
图10 d·L-1 = 0.15 条件下畸形波生成、演化过程中不同代表点波面时间过程Fig. 10 Time-process of water-surface elevation at different representative positions

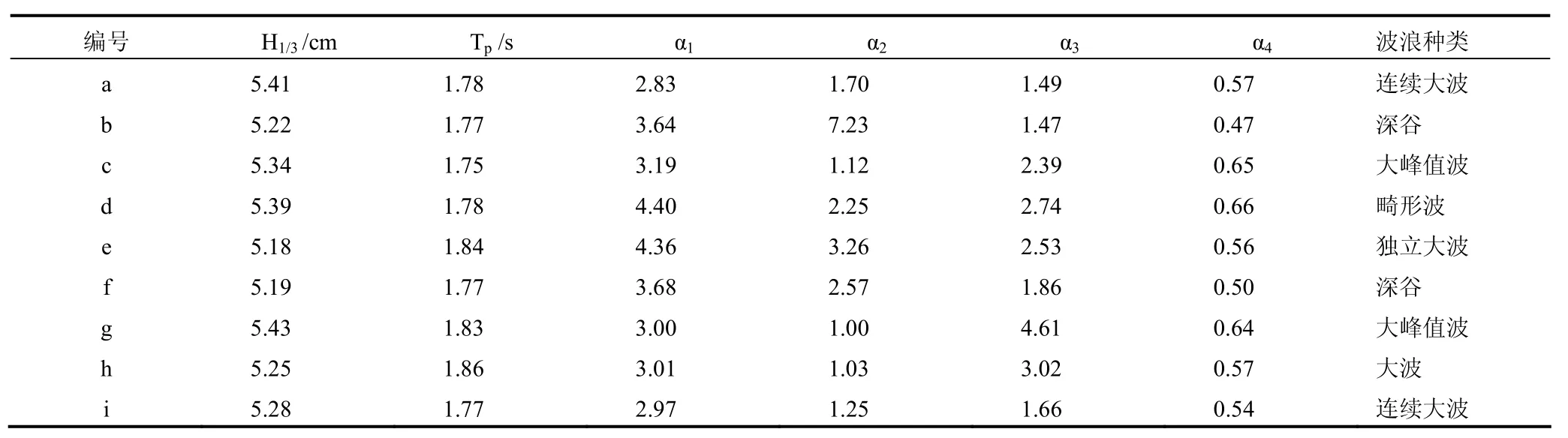
表8 d·L-1 = 0.15 条件下畸形波生成、演化过程中出现的极端波浪的相关参数值Tab 8 Coefficient values for the extreme waves

表9 深谷相关参数值Tab 9 Coefficient values for the deep troughs

该畸形波的生成、演化过程与前面3组畸形波的生成、演化过程完全类似（与新年波的生成、演化过程的不同之处为：畸形波演化过程包含满足条件α1＞2和α3＞2的大波），不赘述，空间范围约6.2倍有效波长，时间长度约 10倍平均周期。无量纲水深d / L 分别为0.28，0.65，0.82条件下模拟的畸形波生成、演化过程与前面结果完全一致，不赘述，空间范围分别为6.2、3.4和4.6倍有效波长，时间长度分别为：11、11和13倍平均周期。表9给出4组人造畸形波生成、演化过程中无量纲深谷最大值。从表9中也可以看出，畸形波生成、演化过程中两次无量纲深谷最大值基本相同。与模拟实测资料得到的结果一致。对比表7和表9中的无量纲波谷值，发现表9中的值都大于等于表7中的值。理论上讲，波浪的波高越大波谷就会相应相对较大。

4 结 论

基于完全非线性波浪数值模型，模拟了畸形波的生成、演化过程，通过对传播波列时间和空间的演变过程的模拟及对波列中异常波浪（畸形波和深谷）特征参数分析，得出如下结论：

（1）畸形波的生成、演化过程为：从连续大波（大波波群）→深谷→畸形波→独立大波→深谷→连续大波。

（2）在本数值计算研究范围内，畸形波生成、演化过程中出的大波、“深谷”和畸形波均具有伴生性，畸形波生成前、后两次形成深谷，其最大值基本相同，深谷非独立异常波浪。

（3）畸形波生成、演化过程的空间范围为3～7倍有效波长，时间长度为9～13倍平均周期。

[1] Osborne A R, Onorato M, Serio M. The nonlinear dynamics of rogue waves and holes in deep-water gravity wave trains [J]. Physics Letters A, 2000, 275(5-6)：386-393.

[2] Stansell P. Distributions of extreme wave, crest and trough heights measured in the North Sea [J]. Ocean Engineering, 2004, 32(8～9)：1015-1036.

[3] Clauss G F. Dramas of the sea： episodic waves and their impact on offshore structures [J]. Applied Ocean Research, 2002, 24(3) ：147-161.

[4] Clauss G F, Hennig J, Schmittner C E. Modelling Extreme Wave Sequences for the Hydrodynamic Analysis of Ships and Offshore Structures [C]. Proceedings PRADS 2004-9th International Symposium on Practical Design of Ships and Other Floating Structures, Travemünde, Germany.

[5] Walker D A G, Taylor P H, Taylor R E. The shape of large surface waves on the open sea and the Draupner New Year wave [J].Applied Ocean Research, 2004, 26 (3～4)： 73-83.

[6] Kriebel D L. Efficient simulation of extreme waves in a Random Sea [C].Abstract for Rogue waves 2000 workshops.Brest, 2000,1-2.[7] Wang Y X. Numerical wave channel with absorbing wave-maker[J].China Ocean Engineering, 1995, 9(2)： 79-88.

[8] Ren B, Wang Y X. Numerical simulation of random wave slamming on structures in the splash zone [J].Ocean Engineering, 2004,31(5-6)： 547-560.

Research on the generation and evolution of freak wave——time-process of the water surface elevations’ variation with positions

CUI Cheng, ZHANG Ning-chuan, PEI Yu-guo

(State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China)

Simulations of generation and evolution of freak wave were carried out based on a fully-nonlinear numerical model. The process of water surface elevation and parameters of freak wave were analyzed consequently. The results showed that freak wave was not an independent abnormal phenomenon, but was very likely accompanied by the successive large waves (huge wave sequence) and deep trough. The potential threat to vessels and maritime structures caused by the combined effect of the extreme waves and deep trough might be far beyond a transient freak, which should be paid more attention.

freak wave; generation and evolution; deep trough

P731.21

A

1001-6932(2011)04-0387-10

2010-09-16；

2011-04-08

国家自然科学基金(11602402-4022-36)；博士后科学基金(20080441115)。

崔成（1984－），男，辽宁海城人，博士。主要从事随即波浪与结构相互作用研究。电子邮箱：chengcui1984@163.com。