双曲型方程的一类并行格式及其数值实验
刘轶中,薛晓鹏
(贵州大学理学院数学系,贵州贵阳 550025)
双曲型方程的一类并行格式及其数值实验
刘轶中,薛晓鹏
(贵州大学理学院数学系,贵州贵阳 550025)
双曲型方程的一般并行格式是采用空间方向并行,时间方向步进的计算方式。本文构造一类恰是时间方向并行,空间方向步进的并行格式,该格式绝对稳定,局部截断误差为o(m2τ2+mτh+h2)。
双曲型方程;并行格式;稳定性;截断误差
构造双曲型方程的并行算法是并行计算研究中极为重要的部分,但由于对双曲型方程的计算具有极强的方向性、不具有绝对稳定的显格式、一般不具有对角占优且仅具有单边边界条件,故对双曲型方程串行差分格式的并行化是一件很不容易的事情,且双曲型方程的并行格式一般是采用空间方向并行,时间方向步进的计算方式,见文献[1-10]。但对于时间方向并行,空间方向步进的并行格式,尚未见到这方面的文献。笔者针对下述的双曲型方程的初边值问题

构造了一类并行格式就是这样一类时间方向并行,空间方向步进的计算格式,该格式绝对稳定,局部截断误差为o(m2τ2+mτh+h2)。
1 构造并行格式
设问题(1)的解u(x,t)充分光滑,于是,由方程(1)可得如下关系式

如果j从0开始,则计算从左往右行;如果j从J-1开始,则计算从右往左行,如此每一次可用并行机同时计算m个函数值…具有良好的并行度。但m的值不宜太大,以免计算误差放大。
2 稳定性分析
对于并行格式(9)的稳定性分析,用Fourier变换,见文献[13],有:
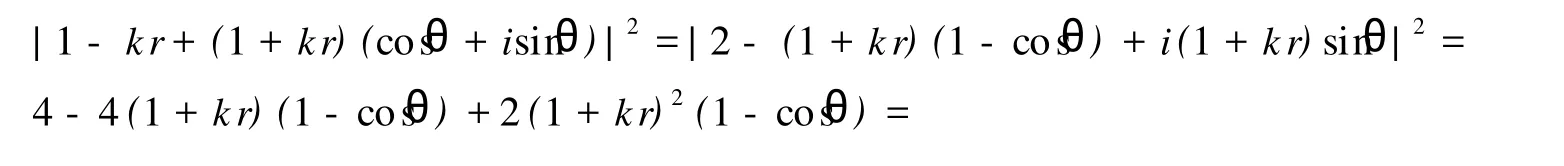

对∀r≠0皆成立,亦即此格式绝对稳定。由此,有:
定理2 对∀r≠0,并行格式(9)绝对稳定。
3 实验报告
3.1 实验目的及要求
(1)有效求解双曲型方程;
(2)通过编程实例计算,验证理论分析的正确性。
3.2 实验(或算法)设计(上已叙述,略)
3.3 实验硬件及软件平台
(1)硬件平台:贵州大学理学院数学系应用数学与建筑力学实验室的方正电脑;
(2)软件平台:VC++6.0。
3.4 实验步骤和实验内容
(1)编写程序(略)
(2)具体数例
考虑双曲型方程的初边值问题


表1 并行格式(9)的误差(r=1.9,m=5,h=0.01)
3.5 实验结果与讨论
以上数值例子表明理论分析是正确的,格式是有效的。
[1] Evans D J,Abdullah A R B.Group explicit method for parabolic equations[J].Inter J Computer Math,1983,14:73-105.
[2] Evans D J.Alternating group explicit method for hyperbolic equations Comput[M].Math.Appl.,1988.15:659-697.
[3] 陆金甫,肖世江.对流方程的 GE方法[J].计算物理,1995,12(3):355-362.
[4] 刘百良.一阶双曲型方程的AGE方法[J].计算物理,1998,15(1):101-106.
[5] 张宝琳,谷同祥,莫则尧.数值并行计算原理与方法[M],北京:国防工业出版社,1999.
[6] 金承日,刘家琦.对流方程的交替分组显式方法[J].哈尔滨工业大学学报,2000,32(1):48-50.
[7] 金承日,丁效华,张少太.双曲型方程的有限差分并行迭代算法[J].哈尔滨工业大学学报,2002,34(3):340-343.
[8] 谭畅,刘播.解双曲型方程的几种并行算法[J].工程数学学报,2004,21(8):155-159.
[9] 方春华,张大凯.双曲型方程的一类分组显示并行算法[J].贵州科学,2006,24(3):11-13.
[10] 刘轶中,张大凯.解双曲型方程的分组并行格式[J].贵州大学学报(自然科学版),2007,24(4):340-344.
[11] 方春华,张大凯.双曲型方程的组合差商解法[J].贵州大学学报(自然科学版),2004,21(2):136-139.
[12] 方春华,张大凯.双曲型方程在乘积型差商空间中的高精度组合差商算法研究[D].贵州大学.
[13] 李荣华,冯果忱.微分方程数值解法[M].北京:高等教育出版社,1997.
A class of parallel schemes and numerical experimen ts for hyperbolic equation
LIU Yi-zhong,XUEXiao-peng
(Department of M athematics,College of Sciences,Guizhou University,Guiyang550025,China)
The general parallel schemes for hyperbolic equation are parallel in the direction of space and stepping in the direction of time.In this paper,it construct a scheme that is exactly parallel computing in the direction of time and stepping in the direction of space.The scheme is absolutely stable.The local truncation error iso(m2τ2+mτh+h2).
Hyperbolic equation;Parallel scheme;Stability;Truncation error
O241.82
:A
1001-9383(2011)02-0001-04
2010-04-22
贵州大学大学生创新性实验计划项目
刘轶中(1973-),男,湖南衡东人,硕士,实验师,研究方向:微分方程数值解,Email:liuyiz2004@126.com.

