钢制内压容器安全系数与试验压力系数研究

刘小宁，潘传九，刘 岑，李 清，吴元祥，张红卫

（1.武汉软件工程职业学院机械制造工程系，湖北武汉 430205；2.武汉工程大学机电工程学院，湖北武汉 430074；3.南京化工职业技术学院机械技术系，江苏南京 210048）

钢制内压容器安全系数与试验压力系数研究

刘小宁1，2，潘传九3，刘 岑2，李 清1，吴元祥1，张红卫1

（1.武汉软件工程职业学院机械制造工程系，湖北武汉 430205；2.武汉工程大学机电工程学院，湖北武汉 430074；3.南京化工职业技术学院机械技术系，江苏南京 210048）

考虑钢制内压容器初始静强度和载荷的不确定性，应用信息熵理论，对容器安全系数、试验压力系数与可靠指标的关系进行探索。研究表明：1）钢制薄壁内压圆筒屈服安全系数应不小于1.50，抗拉安全系数应不小于1.90；钢制薄壁内压球形容器屈服安全系数应不小于1.40，抗拉安全系数应不小于2.15；扁平绕带式容器屈服安全系数应不小于1.45，抗拉安全系数应不小于2.40；超高压厚壁圆筒抗拉安全系数应不小于2.55。2）钢制内压容器试验压力系数在气压与液压试验时应不小于1.07。3）钢制薄壁内压圆筒试验压力系数在气压试验时应不大于1.20，在液压试验时应不大于1.35；钢制薄壁内压球形容器试验压力系数在气压试验时应不大于1.18，在液压试验时应不大于1.32；扁平绕带式容器试验压力系数在气压试验时应不大于1.24，在液压试验时应不大于1.41；超高压厚壁圆筒试验压力系数在液压试验时应不大于1.66。

内压容器；可靠指标；失效准则；安全系数；试验压力系数

考虑钢制内压容器初始静强度（屈服与爆破强度）的不确定性，对容器进行可靠性设计是压力容器领域研究的热点与前沿课题。

许琦、赵亚凡、王剑彬、赵建平和胡宽等分别考虑随机或模糊不确定性，对钢制内压容器可靠性设计与安全评定方法进行探讨［1－5］，但没有充分考虑中国压力容器标准［6－9］的影响；文献［10］—文献［15］基于中国压力容器标准，研究了钢制薄壁内压圆筒形容器与球形容器、扁平绕带容器和超高压厚壁圆筒初始静强度与载荷的分布规律和分布参数，同时考虑容器初始静强度的随机与模糊不确定性，从等可靠度的观点确定容器在压力试验和正常操作时的可靠指标［16］。

尽管考虑随机或模糊不确定性的可靠性设计方法并不需要安全系数，但是，中国压力容器标准是采用确定性设计方法进行压力容器设计，因此，借用可靠性设计方法中的可靠指标确定安全系数与试验压力系数，可推动压力容器设计技术的进步。

笔者根据容器在压力试验和正常操作时的可靠指标，应用信息熵理论，对钢制内压容器安全系数、试验压力系数与可靠指标的关系进行探索。

1 理论模型

钢制内压容器初始静强度，是指不考虑腐蚀等因素影响时的初始屈服和爆破强度；容器的载荷是指容器的试验压力或工作压力。容器的可靠指标是指度量许用可靠度的数值指标，是进行压力容器可靠性设计与安全评定的基础，按中国标准得到可靠度系数是确定可靠指标的依据。

钢制内压容器初始静强度的不确定性，是随机性与模糊性造成的，因此可将其视为模糊变量。由于初始静强度与载荷的隶属函数基本符合正态分布，基于信息熵中模糊等效随机原理［16］，可得可靠指标与初始静强度和载荷分布参数的关系：

式中：［β］r为可靠指标，在屈服与爆破准则下分别为［β］s与［β］b；ηr为模糊屈服与爆破强度统计量的均值，在模糊屈服与爆破强度时分别取ηs与ηb；［k］r为载荷与名义初始屈服或爆破强度之比的许用值，在屈服与爆破准则时分别取［k］s与［k］b；Vr，VL分别为模糊静强度与模糊载荷等效随机的变异系数，在压力试验与正常操作时的取值不同。

式中：σr1，σr2分别为内筒与绕带材料的机械性能，在屈服和爆破失效准则下分别为σs1与σs2，σb1与σb2；K1，K2分别为内筒与绕带层径比；α为绕带的缠绕倾角。

对于超高压厚壁圆筒，

在正常操作与压力试验时，有

式中λ为试验压力系数，正常操作时λ＝1.00。

把式（7）代入式（1）中可得

2 分布参数与可靠指标

内压容器初始静强度的分布参数见表1［16］。容器载荷的分布参数是［16］：气压试验VL＝0.036 45，液压试验VL＝0.039 36，正常操作VL＝0.064 18。

内压容器初始静强度在压力试验和正常操作时的可靠指标［16］见表2。

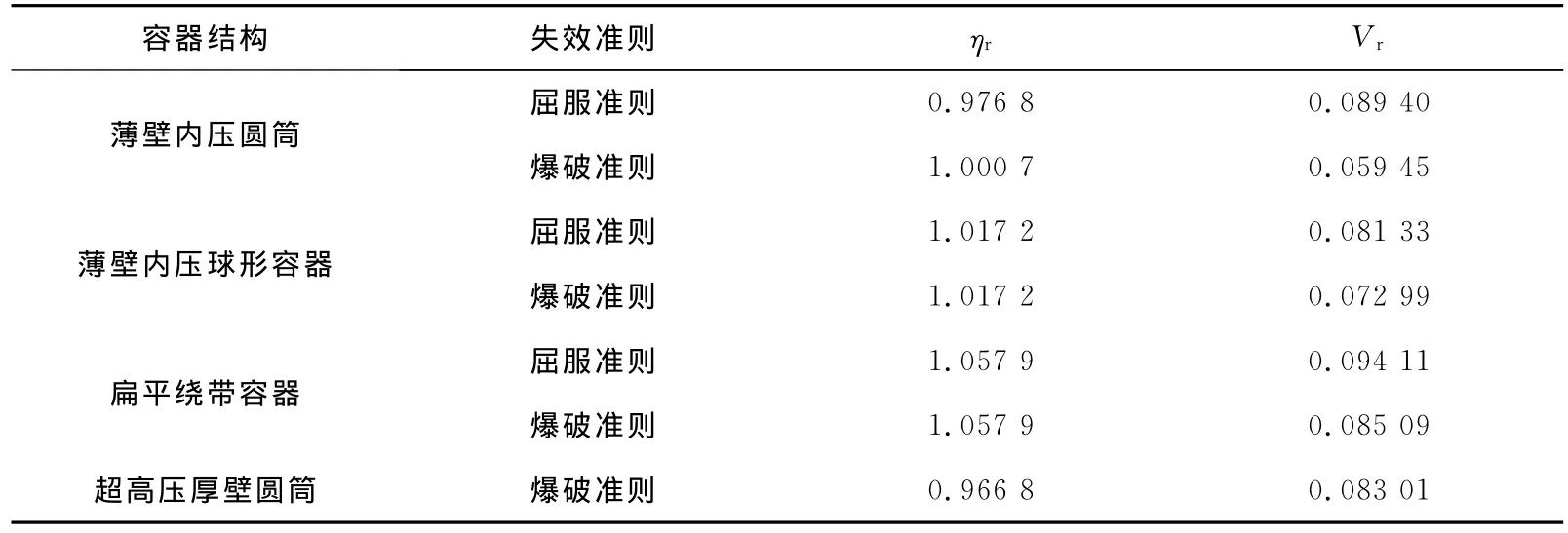
表1 ηr与Vr的取值Tab.1 Values ofηrand Vr

表2 内压容器的可靠指标Tab.2 Reliable indexes of intrinsic pressure vessel

3 安全系数与试验压力系数

3.1 安全系数的初选值

在正常操作时，把表1、表2和有关数据代入式（9），并取λ＝1.00，可得安全系数的计算值与初选值，见表3。

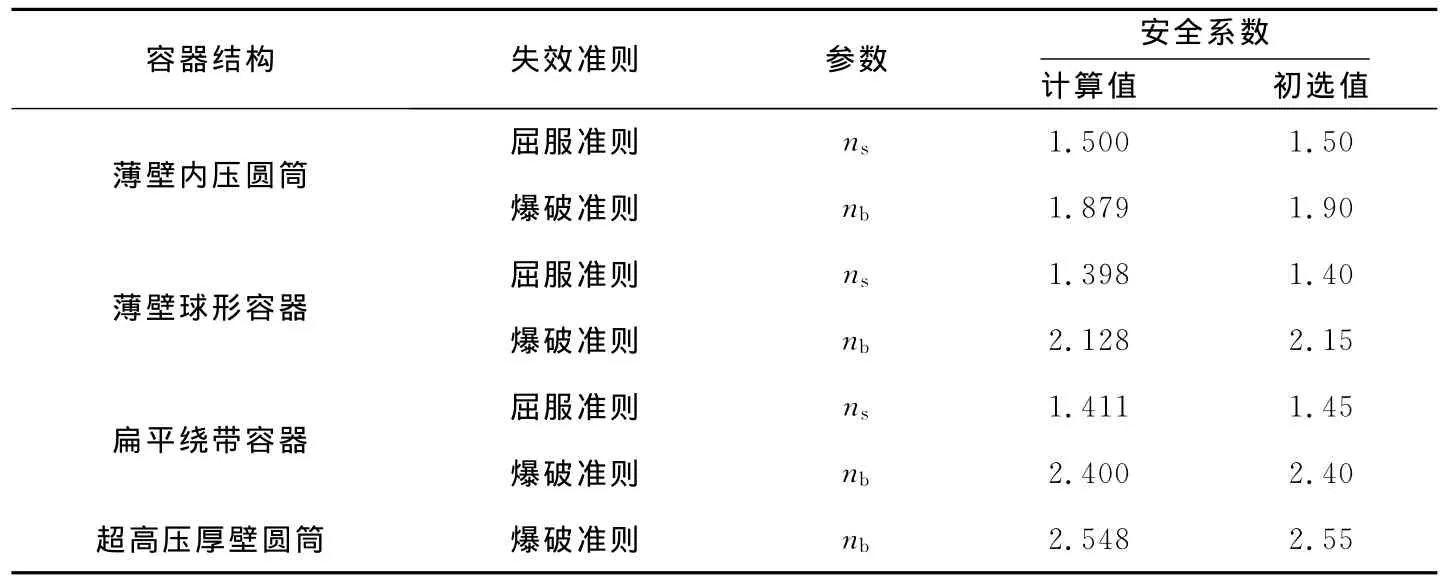
表3 安全系数的初选值Tab.3 Primary selected value of safety factor

3.2 试验压力系数的取值范围

把表1、表2和有关数据代入式（11），可得试验压力系数下限值λ＝1.07。

把表1－表3和有关数据代入式（10），可得试验压力系数上限值，见表4。

表4 试验压力系数上限值Tab.4 Higher limit of test pressure coefficient

由表4和以上分析可知：

1）文中得到的试验压力系数取值范围与中国压力容器标准基本一致，因此，可以把表3中的安全系数初选值作为安全系数的最小值；

2）除超高压厚壁圆筒外，其余结构容器的试验压力系数上限是由屈服失效准则控制的；

3）中国压力容器标准［8］将薄壁内压容器的安全系数降到ns＝1.50与nb＝2.40，有一定的理论与实践基础。

4 结 语

1）以按中国标准设计、制造、检验和监察的钢制薄壁内压圆筒、薄壁球形容器、扁平绕带容器及超高压厚壁圆筒为研究对象，考虑其初始静强度与载荷的不确定性，应用信息熵理论，在压力试验和正常操作时，探索得到安全系数、试验压力系数与可靠指标的定量关系。

2）根据等可靠度观点确定的可靠指标，得到钢制薄壁内压圆筒、薄壁球形容器、扁平绕带容器及超高压厚壁圆筒等4种结构压力容器的安全系数与试验压力系数。

3）钢制薄壁内压圆筒屈服安全系数应不小于1.50，抗拉安全系数应不小于1.90；钢制薄壁内压球形容器屈服安全系数应不小于1.40，抗拉安全系数应不小于2.15；扁平绕带容器屈服安全系数应不小于1.45，抗拉安全系数应不小于2.40；超高压厚壁圆筒抗拉安全系数应不小于2.55。

4）钢制内压容器试验压力系数在气压与液压试验时应不小于1.07。薄壁内压圆筒试验压力系数在气压试验时应不大于1.20，在液压试验时应不大于1.35；钢制薄壁内压球形容器试验压力系数在气压试验时应不大于1.18，在液压试验时应不大于1.32；扁平绕带式容器试验压力系数在气压试验时应不大于1.24，在液压试验时应不大于1.41；超高压厚壁圆筒试验压力系数在液压试验时应不大于1.66。

［1］ 许 琦.可靠性设计方法在压力容器设计中的应用［J］.机械设计与制造（Machinery Design ＆ Manufacture），1999，36（1）：6-8.

［2］ 赵亚凡.可靠性设计方法在压力容器设计中的应用及探讨［J］.机械设计与制造（Machinery Design ＆ Manufacture），2002，39（4）：5-6.

［3］ 王剑彬.压力容器的模糊可靠度计算［J］.核动力工程（Nuclear Power Engineering），2000，21（6）：481-483.

［4］ 赵建平.压力容器概率安全评定失效准则研究［J］.化工设备与管道（Process Equipment ＆Piping），2000，37（5）：15-17.

［5］ 胡 宽，常新龙，杨海生.推进剂贮存容器J积分安全评定与寿命预测［J］.机械设计与研究（Machine Design ＆Research），2010，26（1）：15-18.

［6］ GB 150—1998，钢制压力容器［S］.

［7］ GB 12337—1998，钢制球形贮罐［S］.

［8］ TSG R0004—2009，固定式压力容器安全技术监察规程［S］.

［9］ TSG R0002—2005，超高压容器安全技术监察规程［S］.

［10］ 刘小宁.钢制薄壁内压圆筒爆破压力的概率分布研究［J］.化工设计（Chemical Engineering Design），2004，14（1）：23-28.

［11］ 刘小宁，叶四合.薄壁内压容器屈服强度的初始可靠度［J］.锅炉压力容器安全技术（Safety Technology of Boiler and Pressure Vessel），2004（4）：32-35.

［12］ 刘小宁.球形容器静强度概率分布研究［J］.石油化工设备（Petro-Chemical Equipment），2004，33（4）：17-19.

［13］ 刘小宁.扁平绕带式压力容器模糊静强度的确定［J］.化工设计（Chemical Engineering Design），2007，17（6）：28-30.

［14］ 刘小宁.超高压圆筒爆破强度的模糊可靠度［J］.石油化工设备（Petro-Chemical Equipment），2005，34（5）：36-38.

［15］ 刘小宁.压力容器设计压力的合理确定［J］.锅炉压力容器安全技术（Safety Technology of Boiler and Pressure Vessel），2003（6）：11-14.

［16］ 张红卫，刘 兵，刘 岑，等.压力容器概率安全评定的可靠指标研究［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2011，32（2）：192-196.

［17］ 刘小宁.钢制压力容器试验压力的模糊可靠性理论［J］.石油机械（China Petroleum Machinery），2008，36（4）：5-9.

［18］ 韩春鸣，张红卫，刘 岑，等.钢制薄壁圆筒外压试验压力的研究［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2009，30（4）：314-318.

Research in safety factor and test pressure coefficient of steel wall intrinsic pressure vessel

LIU Xiao-ning1，2，PAN Chuan-jiu3，LIU Cen2，LI Qing1，WU Yuan-xiang1，ZHANG Hong-wei1
（1.Department of Mechanical Manufacture Engineering，Wuhan Polytechnic College of Software and Engineering，Wuhan Hubei 430205，China；2.School of Mechanical and Electrical Engineering，Wuhan Institute of Technology，Wuhan Hubei 430074，China；3.Department of Mechanical Technology，Nanjing College of Chemical Technology，Nanjing Jiangsu 210048，China）

Due to the uncertainty of the steel wall intrinsic pressure vessel initial static intensity and the loads，based on the application of information entropy theory，the relationship of the safety factor，the test pressure coefficient and the reliable index were analyzed.The research indicates that：1）For cylinder vessel，the yield safety factor should be no less than 1.50and the burst safety factor no less than 1.90；for spherical vessel or spherical head，the yield safety factor should be no less than 1.40 and the burst safety factor no less than 2.15；for flat ribbon-wound pressure vessel，the yield safe factor should be no less than 1.45and the burst safety factor no less than 2.40；for super-high pressure thick wall cylinder，the burst safety factor should be no less than 2.55.2）The test pressure coefficient of steel wall intrinsic pressure vessel should be no less than 1.07under barometrical and hydraulic pressure tests.3）The test pressure coefficient of cylinder should not be greater than 1.20for barometrical pressure tests，and not greater than 1.35for hydraulic pressure tests；the test pressure coefficient of spherical vessel should not be greater than 1.18for barometrical pressure tests，and not greater than 1.32for hydraulic pressure tests；the test pressure coefficient of flat ribbon-wound pressure vessel should be not greater than 1.24for barometrical pressure tests，and not greater than 1.41for hydraulic pressure tests；the test pressure coefficient of super-high pressure thick wall cylinder should not be greater than 1.66for hydraulic pressure tests.

intrinsic pressure vessel；reliable index；failure criteria；safety factor；test pressure coefficient

TH49；TQ051

A

1008-1542（2011）04-0321-05

2011-01-01；

2011-03-29；责任编辑:冯 民

武汉市教育局重点科研项目（2008K027）；武汉市创新人才开发资金重大创新专项资助项目

刘小宁（1963-），男，湖北武汉人，教授，教授级高级工程师，主要从事机械结构、压力容器可靠性等方面的教学和研究。