一种求解TSP问题的混合算法

谷文祥，李向涛，王春颖，李国媛，殷明浩

（东北师范大学计算机科学与信息技术学院，吉林 长春 130117）

一种求解TSP问题的混合算法

谷文祥，李向涛，王春颖，李国媛，殷明浩

（东北师范大学计算机科学与信息技术学院，吉林 长春 130117）

结合粒子群算法、蚁群算法、重力搜索算法提出了一种新的混合算法——TSP-GPAA.该算法将粒子群算法和重力搜索算法加入到蚁群算法中，利用粒子群算法的全局搜索能力解决了蚁群算法的初始信息素匮乏的问题，并且重力搜索算法将粒子群算法和蚁群算法参数进行优化，明显提高了蚁群算法的优化性能.实验表明新算法对于解决TSP问题是有效的.

蚁群算法；粒子群算法；重力搜索算法；旅行商问题

0 引言

TSP问题是一个重要的组合优化问题，已经被证明是NP完备的.任何能使该问题的求解得以简化的方法，都会受到高度的评价和关注.虽然目前存在一些可以精确地求解TSP问题的算法，但针对大规模的TSP问题，这些算法往往不能胜任.为了解决这一问题，研究人员提出了多种智能算法来处理TSP问题，目前被广泛使用的有遗传算法［1－3］、人工神经网络方法［4］、粒子群算法［5－7］、模拟退火算法［8］、蚁群算法［9］等.然而，这些算法大多不尽如人意，容易陷入局部极小或收敛过慢等问题.近些年，研究人员发现几种智能算法灵活的组合可以为求解TSP提供更好的启发式信息，并且这类混合算法在处理TSP问题上可以提供更有效的行为和更高的灵活性.鉴于以上的原因，混合的智能算法越来越受到人们的关注.由于混合智能算法的研究还处于起步阶段，所以，研究用混合智能算法解决TSP问题是必要的.

蚁群算法是由意大利学者M.Dorgo，V.Maniezzo和A.Colorni于20世纪90年代初提出的一种新型的智能优化算法，已经被应用到TSP问题［10－12］，并且取得一定的效果.它采用了一种正反馈机制，通过信息素的不断更新，最终收敛于最优解.但是，在算法的初级阶段信息素匮乏，导致了求解速度较慢.并且，该算法是典型的概率算法，算法中的参数设定通常是由试验方法确定，这也导致了算法的优化性能要与人的经验密切相关，很难达到算法性能最优.

虽然现在有很多文章是采用混合的算法去解决TSP，但是目前还没有人结合蚁群算法、粒子群算法、重力搜索算法这三种算法解决TSP问题.粒子群算法是一种全局优化算法，虽然在求解组合优化问题的方面稍显逊色，但是由于初始粒子的随机分布这一特点，将其用于组合优化问题时，该算法仍具有较强的全局搜索能力和较快的求解速度.另一方面由Rashedi和Hossein提出的重力搜索算法由于其在逼近最优解时速度较快［13］，可以有效对系统的参数进行优化.综合以上的原因，本文提出了一种结合上述三种算法的混合智能算法：TSP-GPAA.在TSP-GPAA算法中，重力搜索算法用于解决蚁群算法参数和粒子群算法参数的优化，粒子群算法则用于解决蚁群算法初级阶段信息素匮乏从而导致求解速度变慢的问题.

1 算法基础

1.1 蚁群算法

该算法通过模拟蚂蚁的觅食行为，找到最优解.蚂蚁觅食的时候会在所走过的路径上留下信息激素，同时信息激素会随时间而挥发.一条路径走过的蚂蚁越多，留下的信息激素越多；反过来，信息激素浓度高的路径上会吸引更多的蚂蚁.通过这种正向反馈，最终将找到一条最优路径.为了避免蚂蚁两次走上同一条路径（非法路径），为每个蚂蚁设置一个禁忌表以记录它已走过的路径.

1.2 粒子群算法

在某一个空间中初始化一群随机的粒子，通过迭代找到最优解.在每一次的迭代中，粒子通过两个极值来更新自己.第一个就是粒子本身所找到的最优解pBest.另一个极值是整个种群目前找到的最优解gBest.

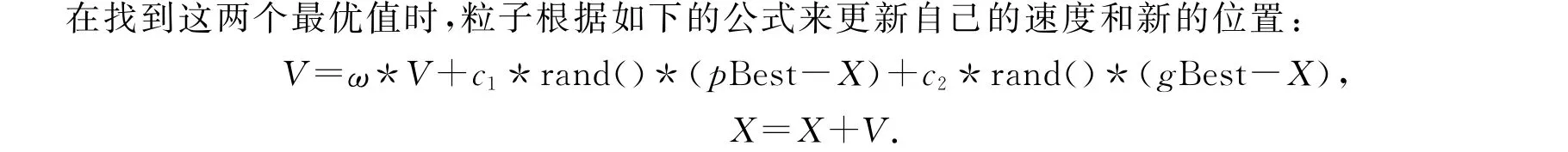
其中：V＝［v1，v2，…，vd］是粒子的速度；X＝［x1，x2，…，xd］是粒子的当前位置；rand（）是（0，1）之间的随机数；c1，c2被称为学习因子，用于调整粒子更新的步长；ω是加权系数.

1.3 重力搜索算法

重力搜索算法（GSA）是由Esmat Rashedi和Hossein Nezamabadi－pour等提出的一种源于对物理学中的策略搜索进行模拟的新的进化技术.初始为一组随机解，通过迭代搜寻最优值，物体在解空间里随着最优的物体进行迭代.

2 TSP-GPAA算法

2.1 对粒子群算法的改进

在标准PSO算法的基础上发展了离散的PSO算法来解决TSP问题［6］.粒子的位置可以定义为序列x＝ ［x1，x2，…，xn，xn＋1］，xi∈E，x1＝xn＋1，当所有xi与xi＋1之间的弧存在 时，速 度定义 为v＝（（i，j）），i，j∈｛1，…，N｝，其中（i，j）是一对置换序列，则速度表示一组置换序列的有序列表.此外，位置与位置之间可以做减法操作，结果为速度；速度与速度间可以做加法操作，结果为速度；位置与速度间可以做加法操作，结果为位置.粒子的位置与位置的加法操作，结果为一组置换序列.速度更新公式为：

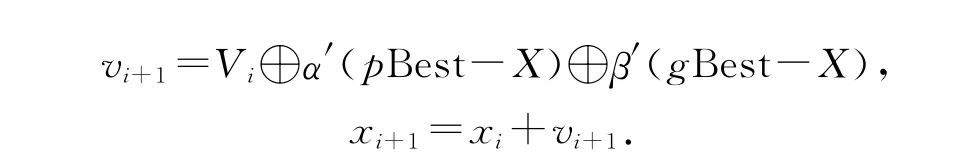
其中：α′，β′为随机数；α′（pBest－X）表示基本交换序中以概率α′保留；同理β′也是类似的作用，⊕为两个交换序的合并因子.

2.2 重力搜索算法对参数的选择

在利用蚁群优化求解TSP问题的过程中，参数α，β，ρ是通过实验确定的，它们对算法性能也有很大的影响.启发式因子α值的大小实际上反映了路径信息素的相对重要性.期望启发式因子β体现了启发式信息在指导蚁群搜索过程中的相对重要性，其大小反映了在寻优过程中先验性、确定因素的作用强度.信息素持久因子ρ反映了蚂蚁个体之间互相影响的强弱.参数α，β，ρ相互配合对蚁群算法性能的影响和作用是密切的.

在利用重力搜索算法对蚁群算法的α，β，ρ和粒子群算法中的α′，β′训练的过程中，物体被表示成一个5维实数编码串，每个物体的位置都是一个潜在的解.将物体的前3维反馈到蚁群系统并按目标函数就可以计算出其适应值，根据适应度的大小衡量解的优劣.将第i个物体的速度也定义为一个5维的向量，记为Vi＝（vi1，vi2，vi3，vi4，vi5），运用重力搜索算法的速度和位置的公式进行更新.

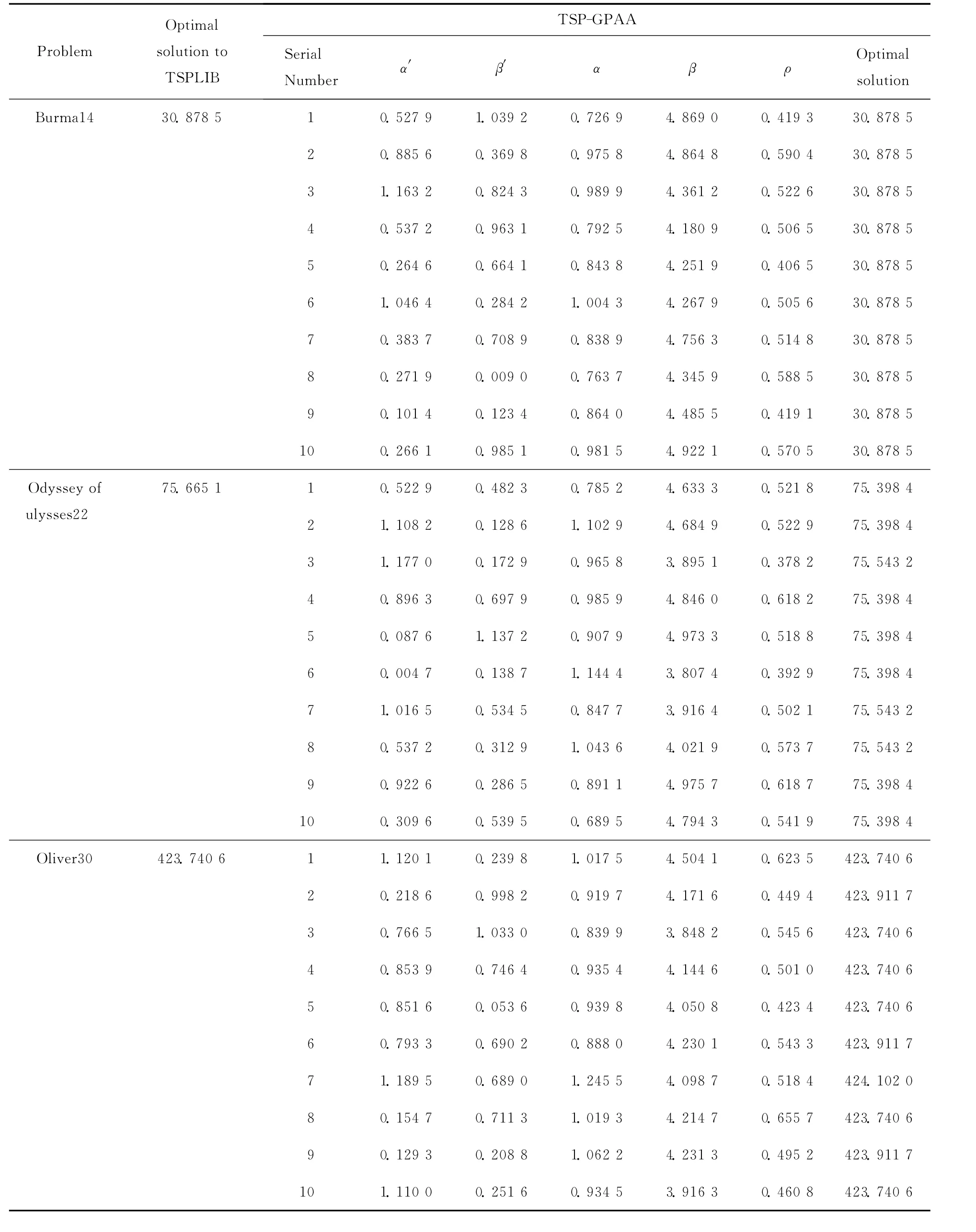
表1 α′，β′，α，β，ρ的参数组合及最优路径

2.3 一种新的TSP-GPAA算法

粒子群算法比较适合求解连续优化问题，在求解组合优化问题上则显得逊色一点.但是，由于其初始粒子的随机分布，使得粒子群算法在解决这类问题时，仍有较强的搜索能力和求解速度.蚁群算法在求解组合优化问题上是优于粒子群算法的，但由于它的信息素开始的时候是一种均匀的分布，使得蚁群算法的早期有着一种盲目性.而重力搜索算法比较适合于解决连续优化问题，我们对两个算法的参数进行训练从而使其能够自适应指导参数的选择.

TSP-GPAA算法的步骤

（1）将改进的粒子群算法中的参数α′，β′和改进的蚁群算法中的参数α，β，ρ作为重力搜索算法入口的调用变量，对其进行转化，然后训练产生一组解.

（2）将这组解的前2维作为粒子群算法的入口参数值，运用改进的粒子群求解TSP问题，迭代n次后，将得到问题的粗解.

（3）利用步骤（2）中得到的粗解调整改进的蚁群算法中信息素的初始分布，运用改进的蚁群算法求解TSP问题，得到问题的最优解.

（4）将步骤（3）运行完成后得到的最优解作为重力搜索算法的适应评价函数，根据适应度的大小调整步骤（1）中的5个参数的值.进入步骤（2）再次训练，找到最优解，从而得出一组参数的值.

（5）重复以上的步骤（1），（2），（3），（4），得到10组能够找到最优解的参数.

由于蚁群算法和粒子群算法以及重力搜索算法都是随机的算法，每次运行的结果都是不一样的，所以应对这些组合再次用蚁群算法和粒子群算法进行训练，从而找到最优解及其参数的最佳组合.

3 模拟实验及结果

为了验证算法的有效性，以TSP标准库中的Burma14，Odyssey of ulysses22和oliver30为例，将10次运行得到的α′，β′和α，β，ρ不同的优化组合及优化路径分别列在同表中.实验中参数m为城市数，Q＝1 000.见表1.

从表1中可以看出10次模拟实验中，对于Burma14最短路径为30.878 5，等于TSP库中给定的值，Odyssey of ulysses22的最短路径最优解为75.398 4，最差值为75.543 2，都优于TSP库中的75.665 1.Oliver30最短路径最优解为423.740 6，最差值为424.102 0，最优解等于 TSP库中的423.740 6.

4 结束语

本文提出的TSP-GPAA算法是结合了蚁群算法、粒子群算法、重力搜索算法的一种混合算法.将粒子群算法和重力搜索算法加入到蚁群算法中，解决了蚁群算法的初始信息素匮乏问题，并将参数进行优化，提高了蚁群算法的优化性能.实验表明所提出的算法对于解决TSP问题是有效的.但由于结合了三种智能算法，其运行的时间较长.并且，我们只对蚁群算法和粒子群算法的部分参数进行选择，因此参数的选择还有待进一步的研究.

［1］ FORGEL D，APPLYING B.Evolutionary programming to selected traveling salesman problem［J］.Cybernetics and System，1993，24：27-36.

［2］ GREFENSTETTE J J.Genetic algorithms for the traveling salesman problems［C］／／Proceedings of an International Conference on Genetic Algorithms and Their Applications，Pittsburgh，USA：1985：160-168.

［3］ FEI LIU，GUANGZHOU ZENG.Study of genetic algorithm with reinforcement learning to solve the TSP［J］.Expert Systems with Applications，2009，5：6995-7001.

［4］ ANDISHEH ALIMORADI，ALI MORADZADEH，REZA NADERI，et al.Prediction of geological hazardous zones in front of a tunnel face using TSP-203and artificial neural networks［J］.Tunnelling and Underground Space Technology，2008，11：711-717.

［5］ SHI X H，LIANG Y C，et al.Particle swarm optimization-based algorithms for TSP and generalized TSP［J］.Information Processing Letters，2007，8：169-176.

［6］ 谷文祥，苏卫华，刘晓龙.构建园区网健壮体系的比较研究［J］.东北师大学报：自然科学版，2010，42（1）：47-52.

［7］ ANGELINE P J.Using selection to improve particle swarm optimization［C］／／IEEE International Conference on Evolutionary Computation，Alaska：Anchorage，1998，5：4-9.

［8］ KLAUS MEER.Simulated annealing versus metropolis for a TSP instance［J］.Information Processing Letters，2007，12：216-219.

［9］ AHMED AL-ANI.Feature subset selection using ant colony optimization［J］.International Journal of Computational Intelligence，2006：53-58.

［10］ WU B，SHI ZZ.An ant colony algorithm based partition algorithm for TSP［J］.Chinese Journal of Computers，2001，24（12）：1328-1333.

［11］ DORIGO M，GAM BARDELLA L.An ant colony algorithm：a cooperative learning approach to the traveling salesman problem［J］.IEEE Trans on Evolutionary Computation，1996（1）：29-41.

［12］ DORIGO M，GAM BARDELLA L L.A study of some properties of ant-Q［C］／／Proc of the 44th Int'1Conf on Parallel Problem Solving from Nature，Berlin：1996：656-665.

［13］ ESMAT RASHEDI，HOSSEIN NEZAMABADI-POUR.GSA：agravitational search algorithm［J］.Information Sciences，2009，7：2232-2248.

A hybrid algorithm for the traveling salesman problem

Gu Wen-xiang，LI Xiang-tao，WANG Chun-ying，LI Guo-yuan，YIN Ming-hao
（College of Computer Science and Information Technology，Northeast Normal University，Changchun 130117，China）

The TSP problem is very important because of its theoretical and practical significance.In this paper，a computationally effective algorithm of combining ACO，PSO and GSA is proposed for solving the TSP problem.In this algorthm，PSO and GSA have been added to ACO.The PSO algorithm solved the shortage problem of the initial pheromone towards ACO.The GSA has been used to choose the Parameters of PSO and ACO.Experimental results show that the proposed algorithm for solving the TSP problem is effective and efficient.

ant colony algorithm；particle swarm optimization；gravitation search algorithm；TSP

TP 301

520·1040

A

1000-1832（2011）03-0060-05

2009-03-07

国家自然科学基金资助项目（61070084，60573067，60803102）.

谷文祥（1947—），男，教授，博士研究生导师，主要从事智能规划与规划识别、形式语言与自动机、模糊数学及其应用研究.

陶 理）