多极化星载SAR模糊比分析与计算

李 延 丁泽刚 郭佳佳

(1 北京空间飞行器总体设计部,北京 100094)

(2 北京理工大学,北京 100081)

1 引言

多极化合成孔径雷达系统是目前世界各国许多合成孔径雷达(SAR)领域的重要发展方向之一。多极化相对于单极化而言,能够提供更多的目标信息和地物散射特性,这也是多极化的最大优点。目前已有不少星载SAR 实现了多极化工作模式,如德国的“陆地合成孔径雷达卫星”(TerraSAR)、加拿大雷达卫星-2(Radarsat-2)等。目前我国也在开展多极化星载SAR系统的研究工作。

星载SAR模糊比(ASR)指模糊性与信号之比,它是系统的一项重要性能参数。单极化星载系统模糊比的计算已经非常成熟了,但对于多极化星载SAR系统而言,其同极化回波与交叉极化回波之间的相互耦合,使得多极化系统的模糊性分析更加复杂,尤其是交叉极化模糊比急剧恶化。因此,为了得到质量满意的图像,分析计算模糊比成为了多极化系统设计的重要问题。

本文详细分析了多极化系统模糊比的计算,推导出了多极化模糊比的计算公式,最后对海洋、森林两种典型目标的模糊比进行了比较。

2 多极化SAR模糊问题

多极化SAR系统的模糊问题与单极化类似,同样分为方位向模糊和距离向模糊。方位向的模糊是由于SAR系统的脉冲工作体制产生的,雷达系统以发射脉冲重复频率(PRF)对方位向采样,使得方位向频谱以PRF为周期搬移,方位向频谱的混叠形成了模糊问题。距离向相差整数个脉冲重复周期(PRT)的回波同时到达接收机,使得距离向产生模糊问题[1],并且多极化系统距离模糊与极化方向有关。

2.1 方位向模糊比

文献[2]中给出了方位向模糊比表达式,与单极化时相同。但多极化系统不同极化方向信号收发时序的组合,形成四种不同的工作时序[3]:交替发射同时接收、交替发射交替接收、同时发射同时接收和同时发射交替接收。为了减小方位向的频谱混叠,不同时序工作模式的PRF 与多普勒带宽的关系也不同,方位向模糊比修正为

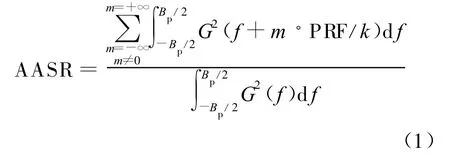
其中,f是回波频率,G(f)为方位向天线功率方向图,PRF为脉冲重复频率,Bp为多普勒带宽,m为回波频率与当前PRF 相差的PRF 整倍数,k 代表不同的工作时序,具体取值如表1所示。

表1 k 在不同工作时序时的取值表Table1 k Value with different working schedule

2.2 距离向模糊比

距离向相差整数个脉冲重复间隔的回波同时到达接收机,使得观测带回波与模糊区回波混叠在一起,产生了距离向的模糊。距离向不同极化方向的电磁波作用目标,产生的回波特性也不同,因此多极化系统的不同工作时序,使得目标的散射矩阵也不同,距离向模糊比的计算也不同。目前的多极化系统多使用交替发射同时接收工作方式,下面就以它为例,分析多极化距离向模糊比。

交替发射同时接收工作方式是交替发射水平(H)、垂直(V)极化波,然后在两个发射脉冲间隔内,同时接收某一极化入射波对应的H、V 散射波。如先发射H 极化波,然后同时接收HH、HV 散射波;接着发射V 极化波,然后接收VH、VV 极化散射波等。因此,相邻模糊区的入射波是正交的,散射波也不同。交替发射同时接收工作方式的模糊区示意模型如图1所示,其工作时序如图2所示。

图1 交替发射同时接收模糊区示意图Fig.1 Ambiguous area illustration w hen transmitting alternately and receiving simultaneously

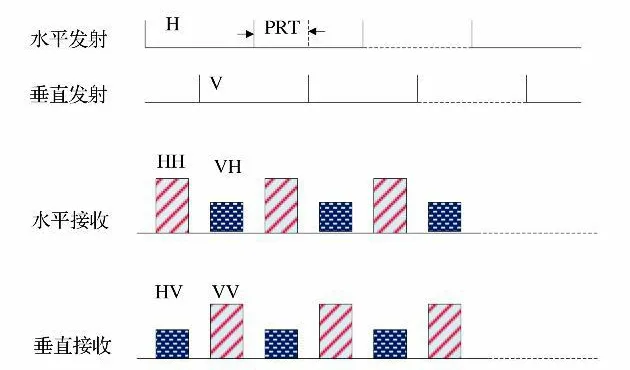
图2 交替发射同时接收时序图Fig.2 Scheduling chart for alternate transmission and simultaneous reception

对于交替发射同时接收工作方式的极化信号而言,在某一回波接收时刻,接收到的信号除了有用信号外,还有正好相差j个PRT 的模糊回波信号。如图1所示,当j为奇数时,该模糊回波信号对应的发射脉冲与有用信号对应的发射脉冲极化方向垂直;当j为偶数时,二者的极化方向相同。因此,考虑距离向模糊对目标散射矩阵的影响,则目标散射矩阵[4]可表示为

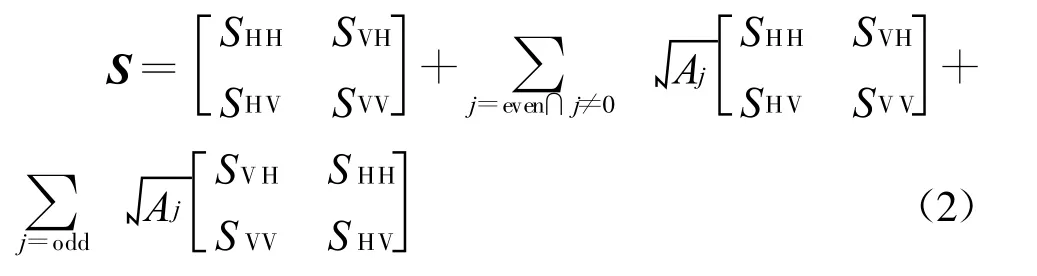
式(2)中,j为模糊区编号,Aj为模糊加权系数且θ为入射角,φ为雷达波束视角,R为模糊区或观测带斜距。

当考虑多极化系统中天线通道间耦合的影响时[5-6],目标散射矩阵修正为

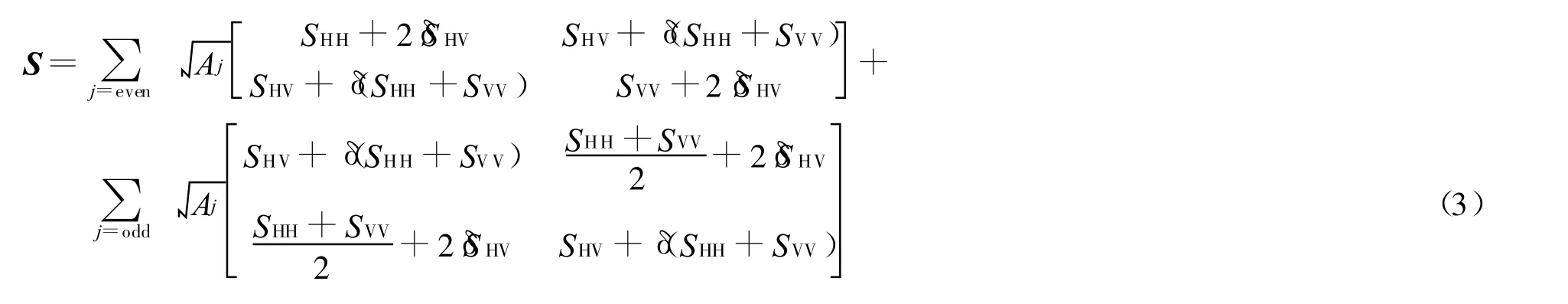
式(3)中,j为模糊区编号,Aj为模糊加权系数,与式(2)中相同,且A0=1。式(3)的推导中利用了互易条件下,散射矩阵为对角阵的特点,即SHV=SVH,具体推导过程见文献[4]。

由散射矩阵与后向散射系数之间的关系,推导得交替发射同时接收工作方式的距离向模糊比表达式如下。

1)HH 同极化模糊比

2)VV 同极化模糊比

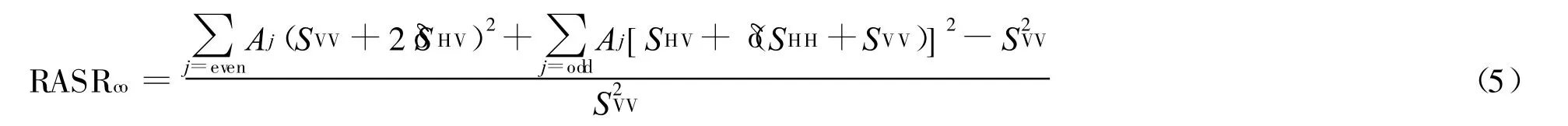
3)交叉极化模糊比

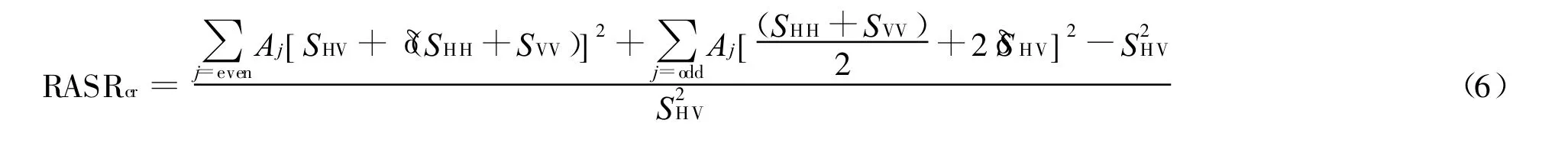
同理,可以分析得到其他三种工作方式距离向模糊比表达式。

3 多极化模糊比与单极化模糊比的比较

单极化系统发射、接收单一极化方向的信号,不需要考虑极化特性的影响,设备简单,模糊比的分析和计算也简单;多极化系统发射、接收信号的极化方式不同,工作时序有四种,使得模糊比的分析和计算需要考虑更多的因素。由上述分析结果可知,多极化与单极化模糊比的分析计算主要有以下3 点不同:

1)方位向模糊比的计算完全类似,只是PRF 的选择与单极化不同,需要考虑工作时序的影响;

2)多极化距离向模糊比需要考虑不同模糊区交叉极化回波和同极化回波之间的相互影响[7];

3)多极化需要发射、接收不同极化方向的信号,故分析计算模糊比时需要考虑天线的极化隔离度的影响。

4 仿真结果

为了验证上述分析,利用Radarsat-2 卫星的SAR系统参数进行仿真计算。系统主要参数及指标如表2所示[8]。以交替发射同时接收工作方式为例,分别对森林、海洋两类目标进行观测。其中森林目标的散射矩阵中,HH 后向散射系数比HV 后向散射系数大5dB[9];海洋目标的散射矩阵中,HH 后向散射系数比HV 后向散射系数大30dB[10]。下面给出森林、海洋两种目标的仿真结果。

表2 Radarsat-2系统主要参数及指标Table.2 Main parameters and their values of Radarsat-2 system

图3～图6是考虑天线通道间耦合对散射矩阵的影响后所得结果。由图3和图4,图5和图6可以看出,交叉极化模糊比比同极化模糊比差,这是由于交叉极化回波受到较强的同极化回波的影响;对比图4与图6可知,海洋目标的交叉极化模糊比由于同极化回波、以及通道间耦合的影响严重恶化,可知海洋交叉极化回波信号不能使用,这也验证了文献[4]中的结论。

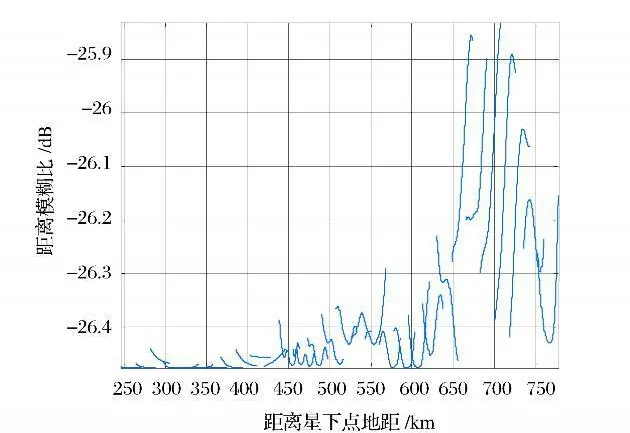
图3 森林目标同极化RAS RFig.3 Mono-polarization RAS R for forest dtarget considering antenna interchannel coupling

图4 森林目标交叉极化RASRFig.4 Cross-polarization RAS R for forest target considering antenna interchannel coupling

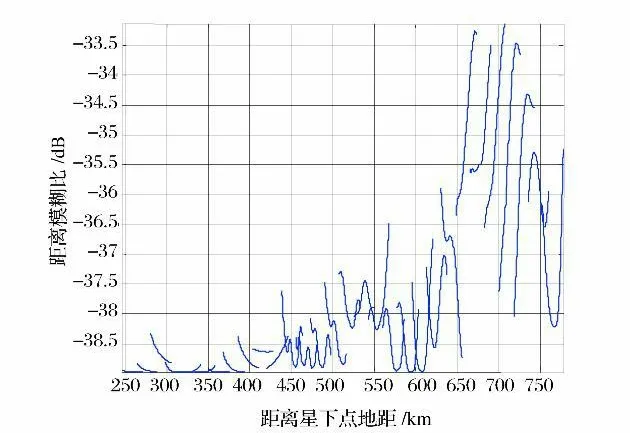
图5 海洋目标同极化RAS RFig.5 Mono-polarization RASR for ocean target considering antenna interchannel coupling

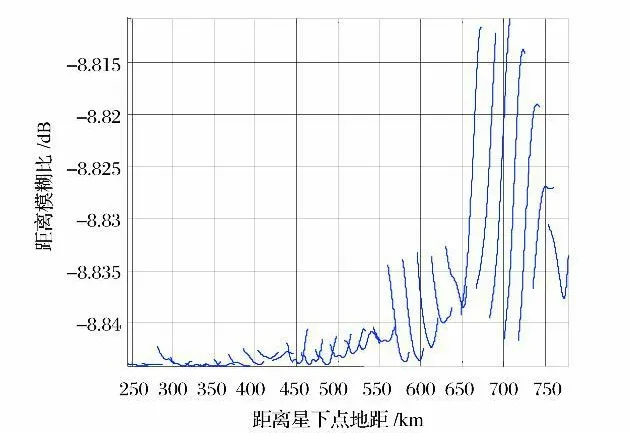
图6 海洋目标交叉极化RAS RFig.6 Cross-polarization RASR for ocean target considering antenna interchannel coupling

当不考虑天线通道间的耦合时,所得结果如图7～图10所示。

图7 森林目标同极化RASR Fig.7 Mono-polarization RAS R for forest target without regard to antenna interchannel coupling

由图7、图8、图9和图10可知,当不考虑天线通道间耦合的影响时,同极化目标比优于交叉极化模糊比5dB,通过多次仿真也验证了这一结论。

5 结束语

本文较详细地分析了多极化SAR系统的模糊问题,给出方位向模糊比公式,同时综合考虑同极化回波和交叉极化回波信号以及天线通道间耦合对观测带有用回波信号的影响,推导了多极化距离向同极化和交叉极化模糊比的计算公式。

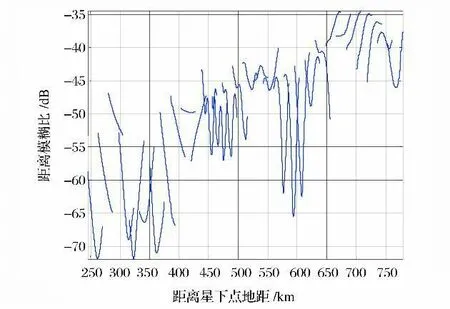
图8 森林目标交叉极化RASRFig.8 Cross-polarization RASR for forest target without regard to antenna interchannel coupling

图9 海洋目标同极化RAS RFig.9 Mono-polarization RASR for ocean target without regard to antenna interchannel coupling

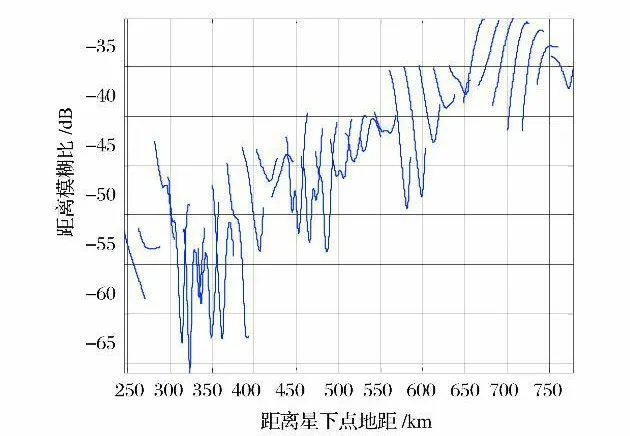
图10 海洋目标交叉极化RASRFig.10 Cross-polarization RAS R for ocean target without regard to antenna interchannel coupling

多极化SAR系统与单极化系统相比,工作时序不同,模糊问题的分析和计算需要考虑更多因素。最后通过对森林和海洋两种典型目标的仿真,验证了海洋交叉极化回波信号模糊严重的问题,为多极化星载SAR系统的设计提供了借鉴。

References)

[1]Li F K,Johnson W T K.Ambiguity in spaceborne synthetic aperture radar systems[J].Aerospace and electronic system s.IEEE Transactions on,1983,19:389-397

[2]戴博伟,杨汝良.多极化合成孔径雷达系统新工作方式及模糊分析[J].电子与信息学报,2001,23 (12):1256-1263

[3]齐向阳.极化合成孔径雷达的模拟研究[D].北京:中科院电子所,2001

[4]Cordey Ralph,Mancini Pierluigi.Range ambiguities for a polarimetric spaceborne SAR[C]//IGARSS＇92:Proceedings of the 12th Annual International Geoscience and Remote Sensing Symposium,Houston,TX,US,26-29 May 1992:637-639

[5]Zyl J J van.Calibration of polarimetric radar images using only images parameters and trihedral corner reflector responses[J].Geoscience and Remoting Sensing,IEEE Transactions on,1990,28:337-348

[6]Freeman A.Calibration of stokes and scatting matrix format polarimetric SAR data[J].Geoscience and Remoting Sensing,IEEE Transactions on,1992,30:531-539

[7]Aria D D'.Awide swath,full polarimetric,L band spaceborne SAR[C]// Rome Italy:In Radar Conference 2008,RADAR' 08,IEEE:1-4

[8]Uher J.Design concepts for the RadarSat-2 SAR antenna[C]//Orlando Florida USA:In Antenna and Propagation Society International Symposium,IEEE,1999,3:1532-1535

[9]刘大伟,孙国清,过志锋.一种基于空间虚拟场景的森林冠层雷达相干散射模型[J].武汉大学学报(信息科学版),2008,33(2):120-123

[10]刘伟,郭立新,王蕊,等.计算二维海面极化电磁散射的新方法[J].西安电子科技大学学报(自然科学版),2009,36(3):517-523