关于一类非零整系数互反多项式的Chebyshev变换

王念良，孔 亮

(商洛学院数学与计算科学系，陕西商洛 726000)

关于一类非零整系数互反多项式的Chebyshev变换

王念良，孔 亮

(商洛学院数学与计算科学系，陕西商洛 726000)

利用第1类、第2类Chebyshev多项式的性质，研究了形如P(n，n)(z)=z2n+1，Q(n，n)(z)=z2n+z2n－2+… +z2+1 的非零整系数互反多项式的 Chebyshev变换，给出了多项式P(mn，mn)(z)，Q(mn－1，mn－1)(z)的 Chebyshev变换公式及一个推论.

第1类Chebyshev多项式;第2类Chebyshev多项式;Chebyshev变换;非零实系数互反多项式

1 引言与结论

2 引理及证明

为了完成定理1的证明，先叙述几个引理.

3 结论的证明

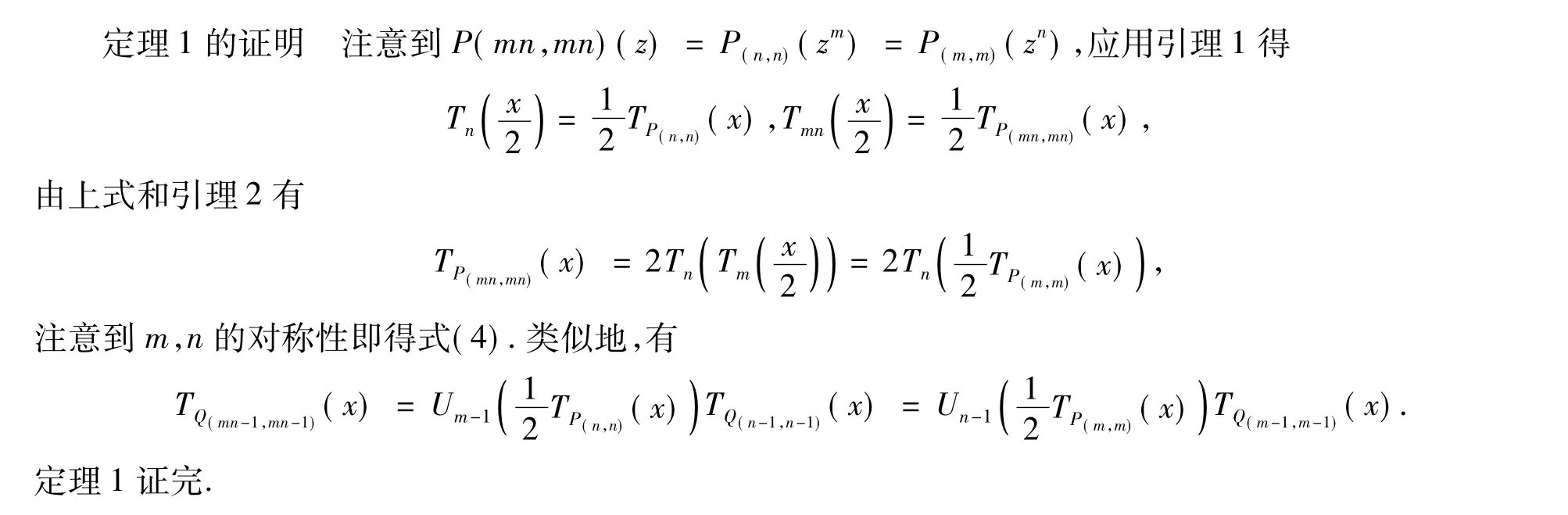
推论1的证明 由式(3)和(4)，不难给出推论的证明(略).

［1］王竹溪，郭敦仁.特殊函数概论［M］.北京:北京大学出版社，2000:171－172.

［2］KANEMITSU S.On Chebyshev polynomials and some of their application［J］.Journal of Shangluo University，2008，22(5):1 －17.

［3］CANNON J W，WAGREIH Ph.Growth functions of surface Groups［J］.Math.Ann.，1992，293:239 －257.

［4］KWON D.Minimal polynomials of some beta-numbers and Chebyshev polynomials［J］.Acta Arithmetica，2007，130(4):321 －332.

［5］LAKATOS P.On zeros of reciprocal polynomials［J］.Publ.Math.Debracen，2002，61:645 －661.

A Kind of Chebyshev Transform of Nonzero Reciprocal Polynomials with Integral Coefficients

WANG Nian-liang，KONG Liang

(Department of Mathematics and Computing Science，Shangluo University，Shangluo 726000，China)

According to the properties of the first kind and the second kind Chebyshev polynomials，Chebyshev transform of some nonzero reciprocal polynomials with integral coefficients such asP(n，n)(z)=z2n+1，Q(n，n)(z)=z2n+z2n－2+ … +z2+1 were studied，and Chebyshev transform formulas on the polynomialsP(mn，mn)(z)，Q(mn－1，mn－1)(z)and a corollary were obtained.

the first kind Chebyshev polynomial;the second kind Chebyshev polynomial;Chebyshev transform;nonzero reciprocal polynomials with real coefficients

O 156.4 < class="emphasis_bold">文献标志码:A

A

1004－1729(2011)01－0001－03

2010－10－09

陕西省教育厅科研计划项目支助(2010JK527);商洛学院科研基金项目(09SKY039)

王念良(1968－)，男，陕西商州人，商洛学院数学与计算科学系副教授.