中国长序列资料测站月降水、月均温相关联系的稳定性分析
姜玉印,楚翠娇
(1.湖北省宜昌市气象局,湖北 宜昌 443000,2.南京大学大气科学学院,江苏 南京 210093)
中国长序列资料测站月降水、月均温相关联系的稳定性分析
姜玉印1,楚翠娇2
(1.湖北省宜昌市气象局,湖北 宜昌 443000,2.南京大学大气科学学院,江苏 南京 210093)
选取我国长序列资料测站点中月降水与月均温资料较全的6个站点:西安、广州、汉口、沈阳、重庆、上海,以10 a为一次成组实验,时域分辨率定为季,计算出各季月降水与月均温的相关系数,然后用相关分析和贝努里概型分析月均温与月降水之间的相关联系,初步得出我国长序列资料测站点春、夏、秋、冬月降水与月均温的相关稳定性联系。结果表明:①我国月降水与月均温在春、夏、秋、冬季均存在相关关系,以夏、秋季节最显著且为负相关,故我国常见干热或湿凉型夏、秋季;②我国华南地区春季月降水与月均温负相关关系显著,故常呈现干热或湿冷型春季;西北地区冬季月降水与月均温负相关关系较为明显,常呈现干热或湿冷型冬季。
相关分析;伯努里概型分析;稳定性;月降水;月均温
1 引言
相关分析作为统计学中重要的一种分析方法在气象中大量应用,文献[1]通过分析黔南自治州降水和干旱、洪涝之间的相关分析,得出了夏季降水与干旱洪涝之间存在着显著的联系。许多学者研究过气温与降水的同期相关及时域特征,文献[2]指出,在100°E以东、30°N以南地区,各季节的降水与气温变化趋势均为反相位。文献[3]指出在全年尺度上降雨量的变化与气温变化基本一致。文献[4]对贵州气温与降水的变化分析发现其相关性具有多时间尺度的特性。本文将对我国月降水与月均温相关系数的稳定性展开分析,由于相关系数在时间域上存在不稳定性[5],因此本文将对其进行检验,找出其稳定存在的规律。
本文选取我国长序列资料测站点中月降水与月均温资料较全的6个站点,运用相关分析和贝努里概型分析我国大部分区域月降水与月均温的相关稳定性联系,检验了我国长序列资料测站点春、夏、秋、冬月降水与月均温的相关稳定性,为揭示我国气候系统中月均温与月降水的同期相关联系提供依据。
2 资料与方法
2.1 资料
由于我国建国以前的气象资料不完整,故本文选取西安、广州、汉口、沈阳、重庆、上海等6个站点月均温与月降水资料连续年代最长且数据完整的月平均气温(T)和月降水量(R)为研究数据,分析我国长序列资料测站月降水、月均温相关联系的稳定性。各站点选取时段分别为:西安(1931-1950年,1951-2000年),广州(1921-1940年,1951-2000 年),汉口(1911-1940 年,1951-2000年),沈阳(1911-1940年,1951-2000年),重庆(1921-1950年,1951-2000年),上海(1911-2000年)。
根据研究目的,以10 a为一次成组实验,由于资料的不完整,某些年代缺少数据,缺省处用999.0补全,每次成组统计中缺省年代不超过2 a;时域分辨率定为季,把每个季节的降水和月均温作平均,然后求出季平均降水与季均温的相关系数,即冬季(12-次年2月),春季(3-5月),夏季(6-8月),秋季(9-11月)。
2.2 方法
本文在计算出西安、广州、汉口、沈阳、重庆、上
海6个站点季平均降水与季均温的相关系数后,用t检验方法检验相关系数的相关性,再由独立实验序列概型-贝努里概型方法判定该系数是否具有稳定性。
2.2.1 相关系数与t检验方法 本文用t检验方法来检验季平均降水与季均温的相关系数是否可信。具体方法为:给定信度α(取α=0.05),根据自由度n-2(取n=10)查出tα,再由(1)式反算出样本相关系数。本文计算的我国长序列资料测站月降水与月均温的样本相关系数=0.63。因此,如果计算得到的∣r∣≥0.63,表示月降水与月均温相关;反之,如果∣r∣<0.63则月降水与月均温不相关。在存在相关时,当r为正时,表示月降水与月均温之间有正相关;r为负时,表示月降水与月均温之间有负相关。∣r∣越大,表示月降水与月均温的关系越密切。

2.2.2 独立实验序列概型-贝努里概型 独立贝努里概型,采用相同的条件下重复地做某试验n次,同时每次试验结果不受其它各次试验影响。由此只要判定其中任何一组数据满足相关性即可说明二者之间存在相关。本文中气温和降水数据为重复独立实验序列,若取n组数据,则气温和降水相关系数存在稳定性的现象出现k次的概率为n
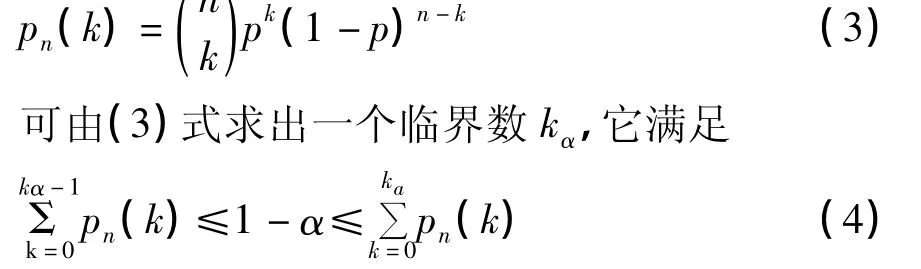
此时,记 γk=kα,则 γ≥γα时,可判‘试验组’所得结果来自非无相关母体。
对于pn(k)的计算问题有两种计算方法,当n取值较大或趋向于无穷大时,采用德莫伊佛—拉普拉斯(Demoive—Laplace)局部极限定理;当n取值较小时,可以直接由(3)式求出pn(K)。
德莫伊佛—拉普拉斯(Demoive—Laplace)局部极限定理:

在此次实验中,由于资料的不完整,n的取值也不完全一致。由上述计算方法编写程序,得出:当n=8,9 时,kα=2;当 n=6,7 时,kα=1。
3 我国月降水与月均温的相关分析
3.1 各站点月降水与月均温的相关分析

表1 西安以10 a为单位的月降水与月均温(1931-2000年)的相关系数
表1给出了西安1931-2000年以10 a为单位的月降水与月均温的相关系数,从该表可以看出:①冬季的7次统计结果中,r7=-0.65,kα=1,存在r<kα,故可认定西安冬季月降水与月均温负相关关系显著,即为干热或湿冷型冬季;②在春季的7次统计结果中,均未通过α=0.05的信度检验(即没有∣r∣≥0.63出现),故春季西安的月降水与月均温不存在相关关系,这种结果在表7中将不被采用;③夏季的7次统计结果中,r1=-0.78,r3=-0.69,r4=-0.67,kα=1,存在 r< kα,所以夏季西安月降水与月均温负相关关系显著,且稳定,即为干热或湿凉型夏季;④同理,在这70 a间,秋季西安的月降水与月均温的相关关系也十分显著,r2=-0.72,r3=-0.79,且呈现负相关,为干热或湿冷型秋季。
由上面的分析可以得出:在春季、秋季、冬季,月降水与月均温呈现负相关关系,即为干热或湿冷型季节,尤其以夏、秋季节更为显著,且在20世纪30年代初至60年代末最为集中。
表2给出了广州1921-1940年、1951-2000年,以10 a为单位的月降水与月均温的相关系数,从表中可以看出:①冬季的7次统计结果均未通过α=0.05的信度检验(即没有∣r∣≥0.63),故冬季广州的月降水与月均温不存在相关关系,此结果将不被采用于表7中;②春季的7次统计结果中,r1=-0.65,r2=-0.70,kα=2,所以春季广州的月降水与月均温的负相关关系显著,即为干热或湿冷型春季;③夏季统计结果中,r1=-0.69,r5=-0.76,r6=-0.72,kα=1,存在 r< kα,所以夏季广州的月降水与月均温的负相关关系十分显著,为干热或湿冷型季节,这点同西北地区一致,并且这一特征都十分明显;④秋季统计结果中,r1=-0.67,所以秋季的月降水与月均温也存在负相关关系,即为干热或湿冷型秋季。

表2 广州以10 a为单位的月降水与月均温(1921-1940年、1951-2000年)的相关系数
上面的分析可以得出:广州春季、夏季、秋季月降水与月均温呈现负相关关系,即为干热或湿冷型季节,且集中在20世纪20年代初到30年代末,以及70年代初到80年代末的夏季,以春、夏季节比较显著。

表3 汉口以10 a为单位的月降水与月均温(1911-1940年、1951-2000年)的相关系数
表3给出了汉口地区1911-1940年、1951-2000年,以10 a为单位的月降水与月均温的相关系数,从表中可以看出:①在冬季和春季的8次统计中,没有任何的∣r∣≥0.63,故冬季和春季汉口的月降水与月均温不存在相关关系,就是说,汉口地区1911-1940年、1951-2000年的冬、春两季月降水与月均温之间无任何相关关系,故此结果将不被采用于表7中;②夏季的统计结果中,r1=-0.66,r2=-0.68,r3=-0.68,n=8,kα=3(在伯努里概型中,当 n=8,9 时,只要kα≥2,月降水与月均温就是相关的),所以在统计的80 a中夏季的月降水与月均温显著负相关,以1911-1930年以及20世纪70年代最为集中,呈现干热或湿凉型夏季;③秋季的8次统计中,没有任何的∣r∣≥0.63,所以秋季汉口的月降水与月均温不存在相关关系,故此结果将不被采用于表7中。
上面的分析可以得出:汉口夏季月降水与月均温呈现负相关关系,即为干热或湿冷型季节,且集中在1911-1930年之间,以及20世纪70年代的夏季,所以从长序列时间来看,华中地区的夏季月降水与月均温是显著负相关的,为干热或湿冷型季节;春、夏、冬季相关性不明显,月降水与月均温之间无相关关系。

表4 沈阳以10 a为单位的月降水与月均温(1911-1940年、1951-2000年)的相关系数
表4给出了沈阳1911-1940年、1951-2000年,以10 a为单位的月降水与月均温的相关系数,从表中可以看出:
①在冬季和春季的8次统计中,没有任何的∣r∣≥0.63,故冬季和春季沈阳地区的月降水与月均温不存在相关关系,就是说,沈阳1911-1940年、1951-2000年的冬、春两季月降水与月均温之间无任何相关关系,故此结果将不被采用于表7中。
②在夏季的统计结果中,r3=0.69,就是说20世纪30年代的夏季统计中,月降水与月均温是正相关的,即干凉或湿热型夏季,但是,从整体的8次统计中,也只有r3=0.69,kα=1,在伯努里概型中,当n=8,9时,kα≥2时才说明月降水与月均温就是相关的,所以沈阳在长时间序列中,夏季月降水与月均温之间不存在相关关系,所以此结果也将不被采用于表7中;③同理,在秋季的8次统计中,也只有r4=-0.81,kα=1,n=8,所以沈阳在长时间序列中,秋季的月降水与月均温之间也不存在相关关系,故此结果将不被采用于表7中,但是在20世纪50年代,由于r4=-0.81,此期间的秋季月降水与月均温之间存在负相关,为干热或湿冷型秋季。
综合上面对沈阳1911-1940年、1951-2000年月降水与月均温相关稳定性的分析,我们可以得出东北地区在此次长时间序列统计中,无论春、夏、秋、冬季节月降水与月均温之间均无相关关系。

表5 重庆以10 a为单位的月降水与月均温(1921-2000年)的相关系数
表5给出了重庆1921-2000年,以10 a为单位的月降水与月均温的相关系数,从统计结果中可以看出:
①在冬季的8次统计中,没有任何的∣r∣≥0.63,故整个80 a期间,重庆冬季的月降水与月均温之间无相关关系,故此结果将不被采用于表7中;②春季统计结果中,在20世纪20年代r1=0.81,r1>0,故1921-1930年间,月降水与月均温呈正相关,即干冷或湿热型春季,但是n=8,在伯努里概型中,当n=8,9时,kα≥2时才说明月降水与月均温就是相关的,而对于重庆的春季统计中,kα=1,所以对于1921-2000年期间,春季月降水与月均温不存在相关关系,故此结果将不被采用于表7中;③在夏季的统计结果中,r5=-0.79,r8=-0.83,当n=8,9时,kα≥2时才说明月降水与月均温就是相关的,所以从长序列时间来看,重庆夏季的月降水与月均温是呈现负相关的,为干热或湿凉型夏季;④秋季的统计结果中,r2=-0.89,即在20世纪30年代,重庆秋季的月降水与月均温是呈现负相关的,为干热或湿冷型秋季,而 r3=0.84,即在20世纪40年代,重庆秋季的月降水与月均温是呈现正相关的,为干冷或湿热型秋季,但从总体来看,n=8,kα=2,所以重庆秋季的月降水与月均温是存在相关性的。
从以上对重庆地区的分析,可以综合得出:从长时间序列来看,西南地区的冬、春季节,月降水与月均温不存在相关关系;夏季、秋季的月降水与月均温之间有相关关系,夏季为负相关,为干热或湿凉型夏季,而春季的正负相关性不明确,要具体时间段具体分析。

表6 上海以10 a为单位的月降水与月均温(1911-2000年)的相关系数
表6给出了上海1911-2000年,以10 a为单位的月降水与月均温的相关系数,从9次的统计结果中可以看出:①在20世纪40年代的冬季,r4=0.69,在此期间月降水与月均温是正相关的,为干冷或湿热型冬季,但是在伯努里概型中,当n=9时,kα≥2时才说明月降水与月均温是相关的,此处kα=1,所以从长序列时间段来看,冬季的月降水与月均温之间不存在相关关系。前10 a的数据资料不完整,但是,可以推测即使前10 a存在完整数据资料,且有相关性,对整个20世纪冬季的月降水与月均温也不构成影响,原因是当n=10时,即使kα=1,也不能说明在此长时间序列中,冬季月降水与月均温之间存在相关性,此结果将不被采用于表7中;②在春季的统计结果中,没有任何的∣r∣≥0.63,所以月降水与月均温之间无相关关系,上个世纪前10 a没有月降水和月均温的数据资料,但是可以推测,即使前10 a存在完整数据资料,无论前10 a月降水与月均温之间的∣r∣是否大于等于0.63,都将对上海在整个20世纪春季的月降水与月均温不产生影响,原因是当n=9,kα=1时,月降水与月均温不存在相关,当n=10,kα=2时,月降水与月均温同样是不存在相关的,故此结果将不被采用于表7中;③在夏季的9次统计结果中,r3=-0.76,r5=-0.69,r8=-0.63,kα=3,所以从长时间序列来看,夏季的月降水与月均温之间存在负相关关系,为干热或湿凉型夏季;④在秋季的统计结果中,也没有任何的∣r∣≥0.63,所以月降水与月均温之间无相关关系,由于上个世纪前10 a没有月降水和月均温的数据资料,但是可以推测,即使前10 a存在完整数据资料,无论前10 a月降水与月均温之间的∣r∣是否大于等于0.63,都将对上海在整个20世纪冬季的月降水与月均温不产生影响,原因是当n=9,kα=1时,月降水与月均温不存在相关,故此结果将不被采用于表7中,这方面同春季、冬季是一致的。
综合上面对上海地区月降水与月均温的分析,可以得出:上个世纪上海的夏季月降水与月均温之间存在负相关,为干热或湿冷型夏季;其他3个季节的月降水与月均温之间相关性不明确,由此可以反映出华东地区的月降水与月均温的相关稳定性情况,即夏季月降水与月均温之间存在负相关,为干热或湿凉型夏季;其他3个季节的月降水与月均温之间相关性不明确。
3.2 我国月降水与月均温的季节变化分析
由于我们采用的样本以资料全面的站点为基础,因此分别以西安、广州、汉口、沈阳、重庆、上海为代表站研究我国西北、华南、华中、东北、西南、华东地区的月降水与月均温的相关稳定性,进而得出我国长序列资料测站点春、夏、秋、冬月降水与月均温的相关稳定性联系。综合以上对各个长时间序列站点在春、夏、秋、冬季月降水与月均温的相关联系的稳定性分析,得出表7,可以看出:
①春季,有一次通过相关检验,是西北地区的月降水与月均温存在相关关系,由于此次检验选定6个站点作统计,只要有一次通过,概率为1/6,此值远大于0.05,所以可以推定,我国在春季的月降水与月均温之间存在相关关系;
②夏季,同样有一次通过相关检验,是华南地区的月降水与月均温存在相关关系,可以推定,我国在夏季的月降水与月均温之间存在相关关系;
③秋季,共有5次通过相关检验,除东北地区以外,选定的其他5个站点均通过,通过率高为5/6,所以推定,我国在秋季的月降水与月均温之间存在显著的相关关系;
④冬季,有3次通过相关检验,分别是我国西北、华南、西南地区,通过率为3/6,故可以推定,我国在冬季的月降水与月均温之间存在显著相关关系;
综合上述对春、夏、秋、冬四季的分析,可以看出:从长时间序列来看,我国大部分地区春、夏、秋、冬季节月降水与月均温之间均存在相关关系;而且夏、秋季节相关关系显著。

表7 我国西北、华南、华中、东北、西南、华东地区长时间序列站点在春、夏、秋、冬季月降水与月均温的相关联系
3.3 我国不同区域月降水与月均温的季节相关性分析
同样是对表7的分析,再结合表1~表6的分析,从另一侧面反映了我国不同区域月降水与月均温的相关性:
①在西北地区,冬季月降水与月均温的相关关系显著,呈负相关,为干热或湿冷型冬季;
②在华南地区,春季月降水与月均温的相关关系显著,亦呈负相关,为干热或湿冷型春季;
③在全国大部分区域的长时间序列中,夏季月降水与月均温的负相关性显著,为干热或湿凉型夏季,但是东北地区的夏季月降水与月均温相关关系不明显;
④在西北、华南、西南地区的长时间序列中,秋季月降水与月均温的负相关性显著,为干热或湿冷型秋季。
4 结论
本文在所采用的数据资料的基础上,综合上面的分析,检验了我国大部分地区春、夏、秋、冬四季的月降水与月均温的相关稳定性联系,得出以下主要结论归纳为:①我国月降水与月均温在春、夏、秋、冬季均存在相关关系,以夏、秋季节最显著且为负相关,故我国常见干热或湿冷型夏、秋季;②同时,华南地区春季月降水与月均温负相关关系显著,呈现干热或湿冷型春季;西北地区冬季月降水与月均温负相关关系较为明显,呈现干热或湿冷型冬季。
由于历史原因,多数长时间序列测站月降水与月均温的数据不完整,本文只能在最大范围内,选取月均温与月降水资料连续年代最长,且数据完整的,故可选站点少,而且存在着个别年代的数据不完整的现象,所以结果存在一定的误差,如果我国长序列资料测站月降水与月均温数据完整,将更完善地验证它们存在的相关关系。
[1] 王政荣,石昌军.黔南近30 a夏季降水变化特征及旱涝关系分析[J].贵州气象,2010,34(3),18-20.
[2] 陈文海,柳艳香,马柱国.中国1951-1997年气候变化趋势的季节特征[J]. 高原气象,2002,21(3),251-257.
[3] 何玲,郭树栋,周华坤.甘德县近10年来气温与降水的变化趋势及相关性分析[J].安徽农业科学,2010(28),15743-15744,15879.
[4] 冷志强,许泊天关于相关系数在时间域上不稳定的初步分析[J]. 贵州气象,1990,24(3),13-16.
[5] 李勇,李德霞.遵义气温与降水变化的多时间尺度对比分析[J].贵州气象,2009,33(2),15-18.
Stability Analysis of the Correlation Between Monthly Precipitation and Monthly Average Temperature in Long Sequence Stations
Jiang Yuyin1Chu Cuijiao2
(1.Yichang Meteorological Bureau of Hubei Province,Yichang443000;2.Nanjing University of Atmospheric Science Department,nanjing210093)
elect six stations of the long sequence data of our country that there are monthly precipitation and monthly average temperature data,namely Xi'an(1931-1950,1951-2000),Guangzhou(1921-1940,1951-2000),Hankou(1911-1940,1951-2000),Shenyang(1911-1940,1951-2000),Chongqing(1921-1950,1951-2000),Shanghai(1911-2000),taking a dacade as an experiment,the hour aera resolution settle for the quarter,compute the related coefficient of monthly precipitation and monthly average temperature,using the related analysis and Bonuly Type,and then get a sequence data of monthly precipitation and monthly average.The result enunciation:①the monthly precipitation and monthly average temperature exists the related relation in our country,especially it is clear in autumn and winter;② it is clear in summer of south region of our country ,preseting the dry heat or wet cool type for summer;and it is clear in spring of nouthwest region of our country,preseting the dry heat or wet cold type for spring.
related coefficient;critical number;stability;monthly precipitation;monthly average temperature
P458
A
1003-6598(2011)03-0007-06
2010-12-23
姜玉印(1981-),女,助工,主要从事短时短期天气预报工作。

