铅芯橡胶隔震支座恢复力模型多因素作用解耦分析结果讨论

钟先锋，刘文光

（1．深圳市建筑设计研究总院有限公司，广东 深圳 518031；2．上海大学，上海 200072）

铅芯橡胶隔震支座恢复力模型多因素作用解耦分析结果讨论

钟先锋1，刘文光2

（1．深圳市建筑设计研究总院有限公司，广东 深圳 518031；2．上海大学，上海 200072）

综合国内外对铅芯橡胶支座力学性能的试验研究成果，考虑各种因素对支座水平方向恢复力模型的影响，提出了主要相关影响因素的修正系数，依次对支座模型进行解耦分析。分析结果可以用来修正常用的铅芯橡胶支座恢复力模型。

铅芯橡胶支座；恢复力模型；多因素耦合作用；解耦分析

引言

隔震结构在地震作用过程中能够表现出良好的隔震效果，使上部结构的加速度比之普通结构降低一个数量级左右，而且实际经验证明隔震结构是一种优良的结构体系。但是，结构中隔震支座的恢复力性能受到较多因素的影响。实验和实际经验表明，支座的竖向压应力、水平位移、加载频率、温度以及使用年限对支座的屈服力和屈服后刚度都会产生较大的影响，而且几种因素相互作用，相互关联，这就给结构分析过程中支座恢复力模型的确定带来一定的困难。《建筑抗震设计规范》GB50011-2010（以下称规范）采用以下方法考虑了上述几种相关因素对支座恢复力模型的影响：对耐久性要求，在经历相应设计基准期的耐久试验后，隔震支座的刚度变化不超过初期值的±20%；对竖向压应力，主要是限制橡胶隔震支座的平均压应力；对水平向减震系数计算，应取剪切变形100%的等效刚度和等效黏滞阻尼比；对罕遇地震验算，宜采用剪切变形250%时的等效刚度和等效黏滞阻尼比，当隔震支座直径较大时可采用剪切变形100%时的等效刚度和等效黏滞阻尼比。规范对模型水平刚度给出了一个设计参考值，但没有给出特定使用条件下的水平刚度值。对隔震结构进行非线性分析时，需要确定支座的屈服力和屈服后刚度，而此两项也同样受到上述几种相关因素的影响，规范对此也没有给出取值标准[1]。这就给不同使用条件下对支座恢复力模型数值的确定带来不便，进而影响结构计算的精度。

针对各种相关因素对支座力学性能的影响，国内外已经进行较多的研究，文献 ［2］［3］研究了铅芯橡胶隔震支座的基本力学性能和长期力学性能，文献 ［4］［5］对其各种相关因素、老化徐变特性和温度性能进行了研究，文献 ［6］给出了日本常用的铅芯橡胶支座各种相关性的试验数据等。然而，上述试验研究虽然指出了各种相关因素的影响，但是没有定量地给出其影响的程度和修正系数，所以还不能运用于实际。

要提高隔震结构设计和分析的可靠性，就要定量把握支座的剪切变形、轴向压应力、加载频率、温度以及橡胶老化等相关因素对支座从微小变形到破坏变形的滞回特性的影响。因此本文综合国内外有关铅芯橡胶支座力学性能的试验数据，针对上述五种因素对隔震支座恢复力模型的影响进行解耦分析，分析结果适用于现有常用的铅芯橡胶支座的恢复力模型。

1 数据拟合和分析方法

由于四次样条曲线摆动小，函数f（x）在区间 （a，b）内光滑，同时经过给定的数据点集 {（xkyk）}Nk=0，所以采用四次样条曲线。通过依次提出各相关因素对铅芯橡胶支座恢复力模型的修正系数来进行多因素解耦分析。思路如下：把试验结果标准化，压力以10 MPa为基准，剪切变形以100%为基准，频率以0.1 Hz的为基准，温度以常温20℃为基准，并把这些情况下的试验结果取值做为标准值 “1”，其它使用条件下的试验结果与之相比，就得到各种不同使用条件下的模型相对于标准条件下的模型的修正系数。

2 铅芯橡胶支座的恢复力模型修正

用双线性模型或者其它一些模型表示铅芯橡胶支座滞回曲线时，可以用屈服后刚度（Ku）和初始刚度 （Kdu）两种弹簧、以及屈服力 （Qd）进行模型化。本文提出的修正内容主要为针对屈服后刚度和屈服力进行的。

2.1 剪切变形相关性

总结文献 ［2］［4］［6］中的剪切变形对支座屈服后刚度和屈服力的影响试验数据，进行归一化处理，取均值，得屈服后刚度、屈服力与剪切变形相关性在试验数据点上的修正系数，如表1和表2。

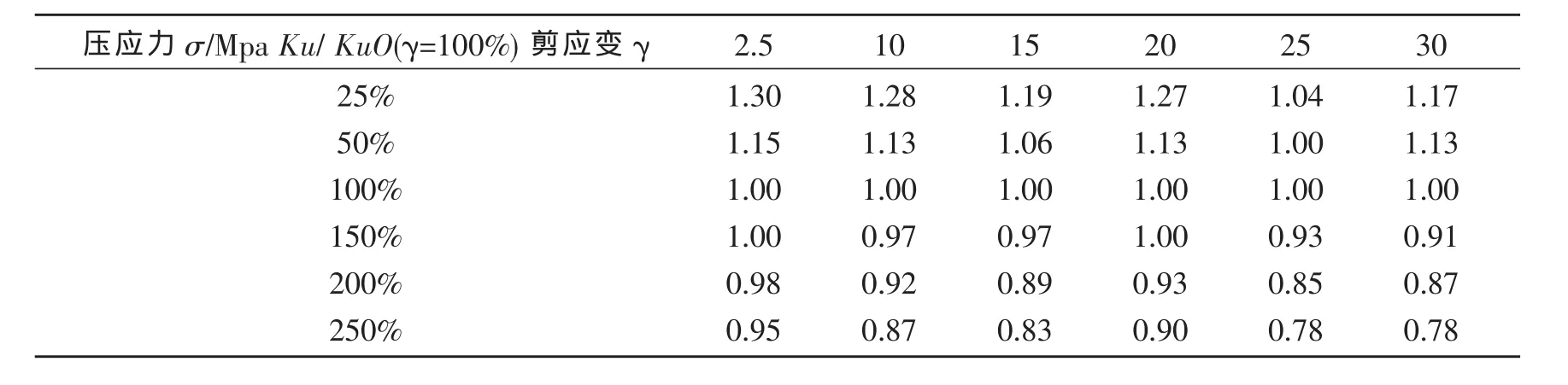
表1 屈服后刚度与剪切变形的相关性在试验数据点上的修正系数表Table 1 Correction parameters of the correlation of yielded stiffness and shear deformation at test data points

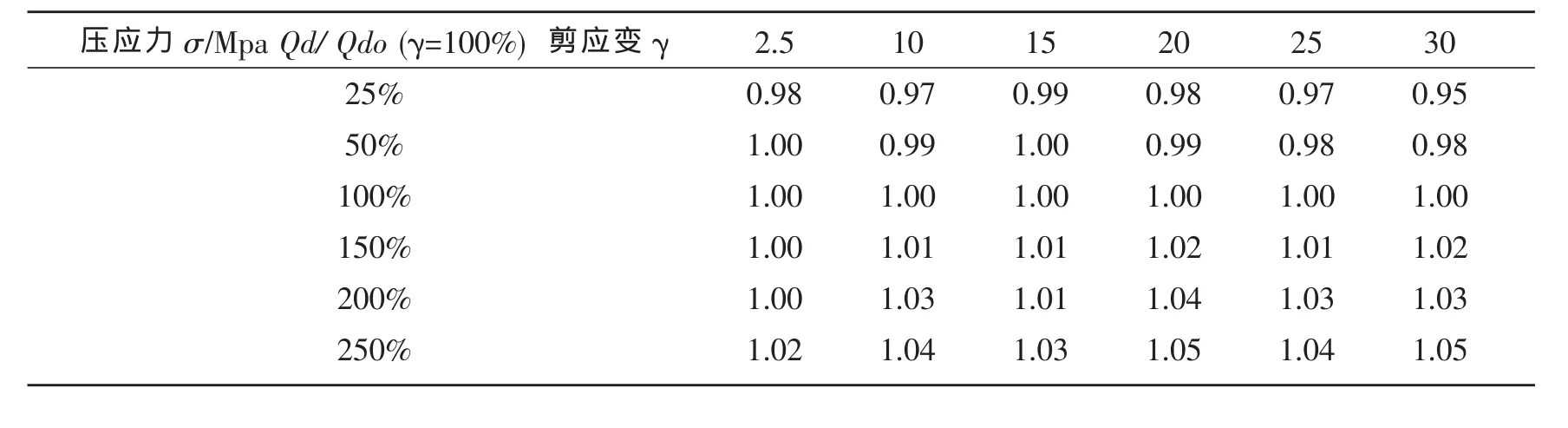
表2 屈服力与剪切变形的相关性在试验数据点上的修正系数表Table 2 Correction parameters of the correlation of yielding strength and shear deformation at test data points

根据表1和表2，采用四次样条曲线对试验数据进行拟合，拟合得屈服后刚度与剪切变形的相关性曲线 （如图1）和屈服力与剪切变形的相关性曲线 （如图2）。拟合公式和拟合参数如表3和表4。

图1 屈服后刚度与剪切变形的相关性曲线图Fig.1 Correlation curve of yielded stiffness and shear deformation

表3 屈服后刚度与剪切变形的相关性计算公式表Table 3 Formulae to the correlation of yielded stiffness and shear deformation

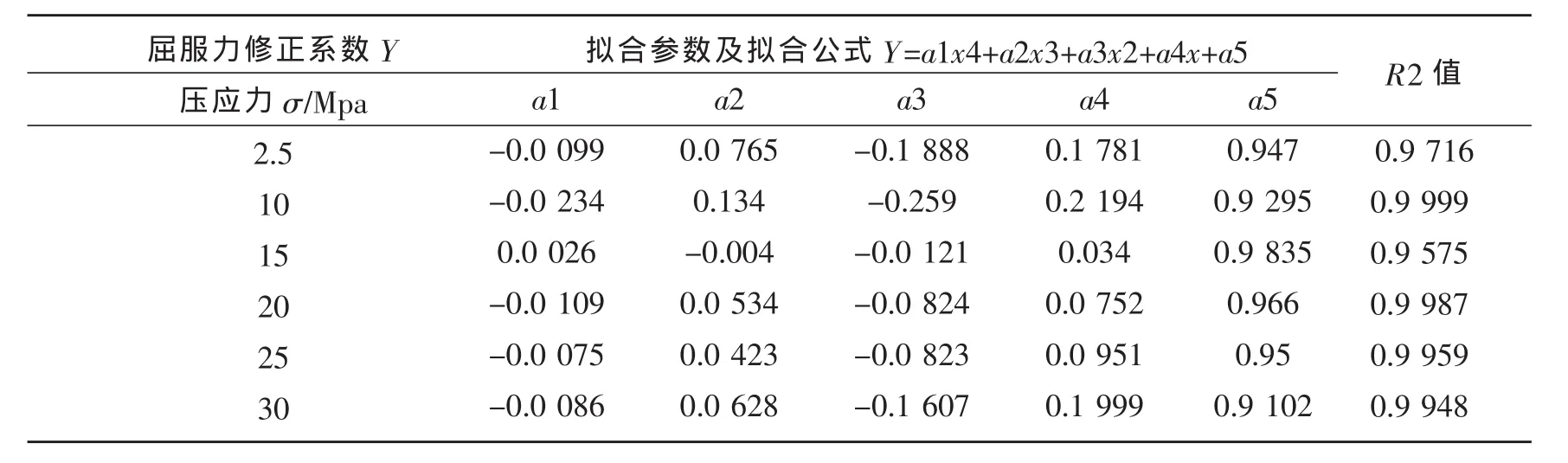
表4 屈服力与剪切变形的相关性计算公式表Table 4 Formulae to the correlation of yielding strength and shear deformation

2.2 压应力相关性

总结文献 ［2］［4］［6］中的压应力对支座屈服后刚度和屈服力的影响试验数据，并对其进行归一化处理，取均值，得屈服后刚度、屈服力与压应力相关性在试验数据点上的修正系数，如表5和表6。

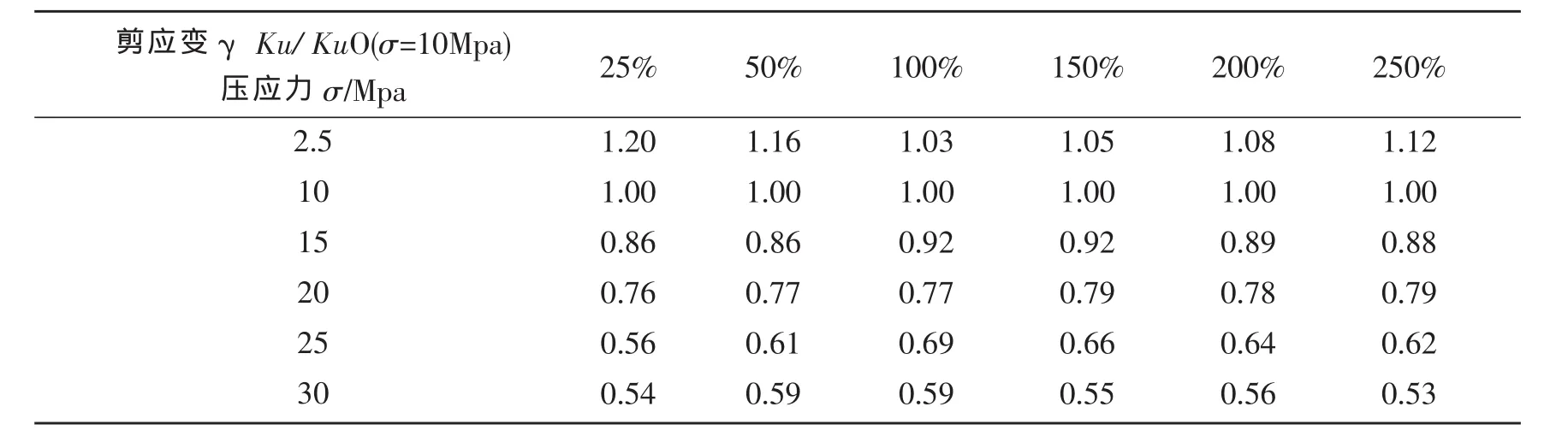
表5 屈服后刚度与压应力的相关性在试验数据点上的修正系数表Table 5 Correction parameters of the correlation of yielded stiffness and compressive stress at test data points

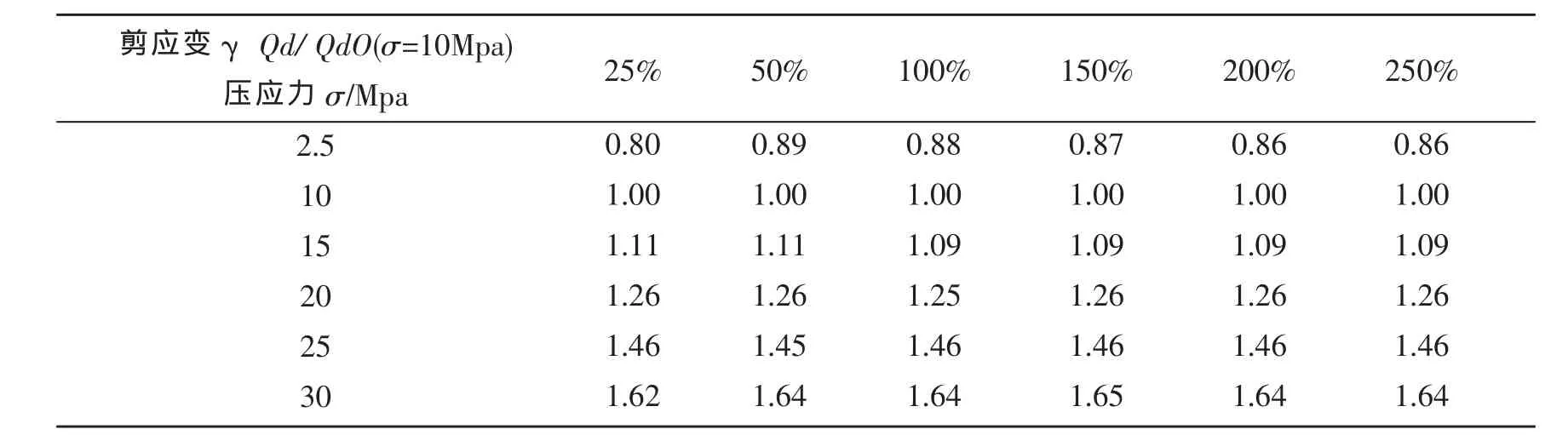
表6 屈服力与压应力的相关性在试验数据点上的修正系数表Table 6 Correction parameters of the correlation of yielding strength and compressive stress at test data points

同样采用样条曲线对表5和表6中归一化后的试验数据进行拟合，拟合得屈服后刚度与压应力的相关性曲线 （如图3）和屈服力与压应力的相关性曲线 （如图4），拟合公式和拟合参数如表7和表8。

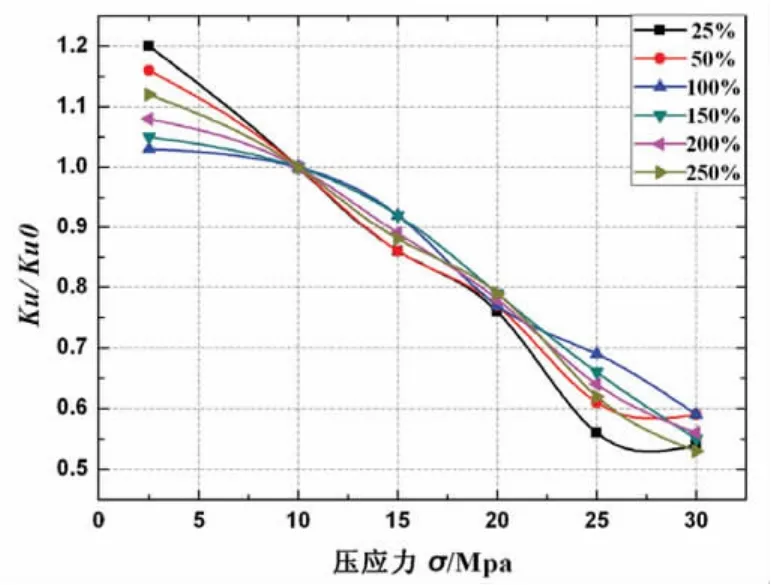
图3 屈服后刚度与压应力的相关性曲线图Fig.3 Correlation curve of yielded stiffness and compressive stress

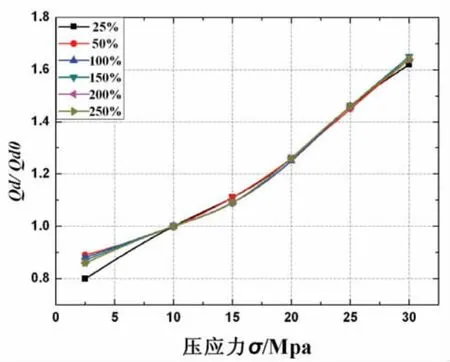
图4 屈服力与压应力的相关性曲线图Fig.4 Correlation curve of yielded stiffness and compressive stress

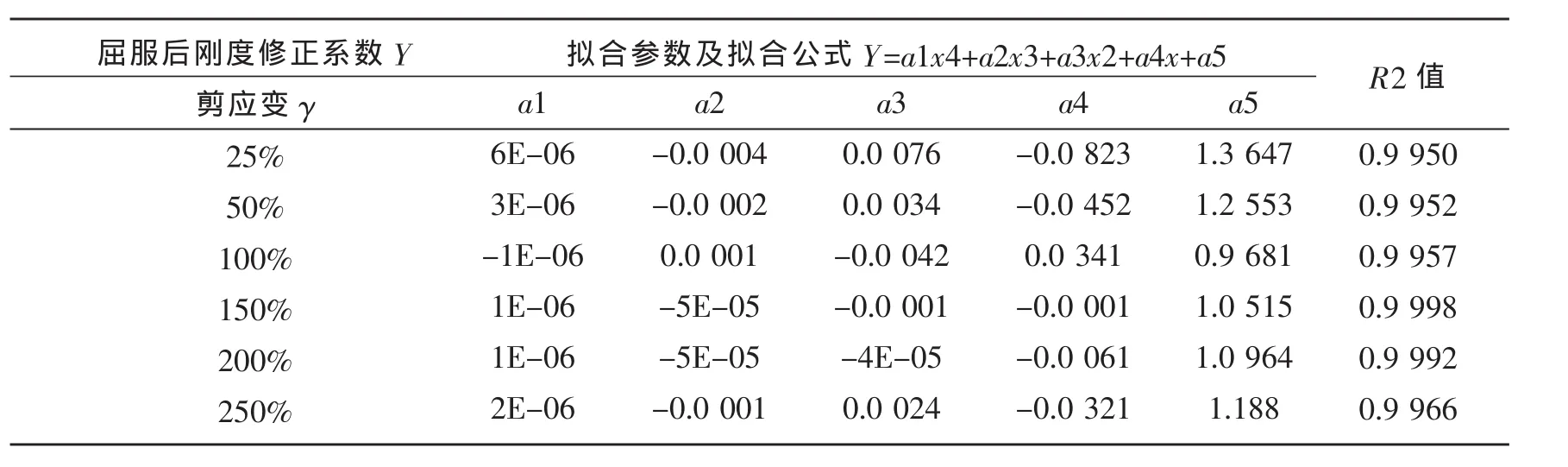
表7 屈服后刚度与压应力的相关性计算公式表Table 7 Formulae to the correlation of between yielded stiffness and compressive stress

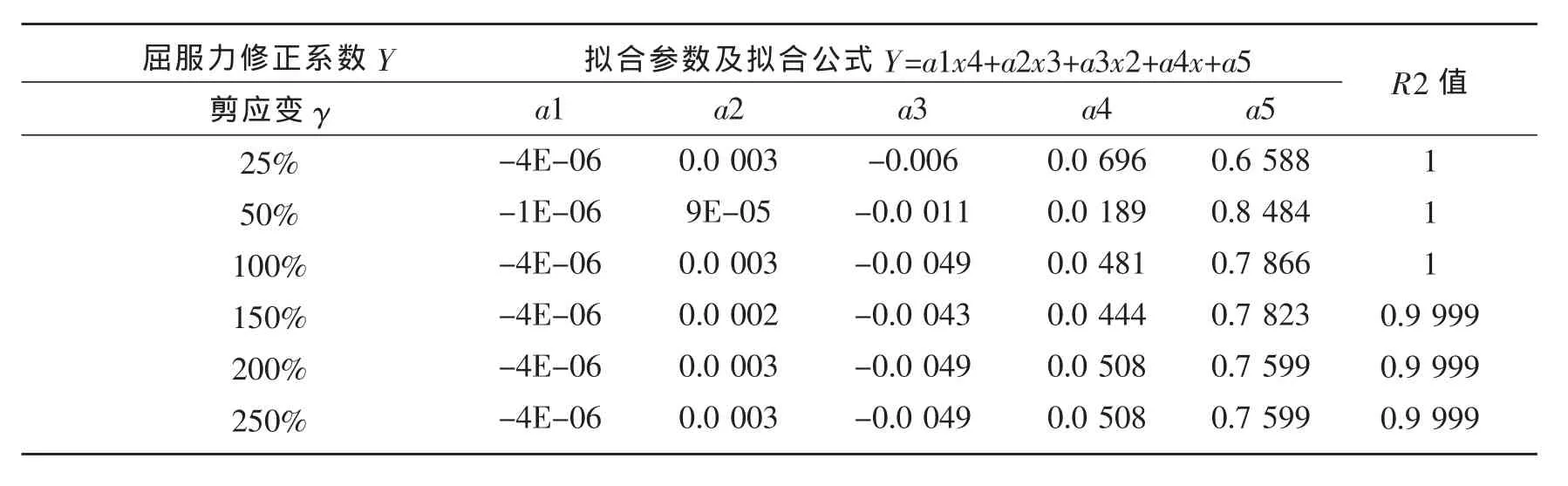
表8 屈服力与压应力的相关性计算公式表Table 8 Formulae to the correlation of between yielded stiffness and compressive stress

2.3 温度相关性

总结文献 ［3］［4］［5］［6］中有关铅芯橡胶支座恢复力模型中屈服后刚度、屈服力与温度的相关性试验数据，进行归一化处理，取均值，得到屈服后刚度、屈服荷载与温度的相关性在试验数据点上的修正系数分别如表9和表10所示。

表9 屈服后刚度与温度相关性在试验数据点上的修正系数表Table 9 Correction parameters of the correlation of yielded stiffness and temperature at test data points

表10 屈服力与温度相关性在试验数据点上的修正系数表Table 10 Correction parameters of the correlation of yielding strength and temperature at test data points

采用样条曲线对表9和表10中归一化后的试验数据进行拟合，拟合得屈服后刚度与温度的相关性曲线 （如图5）和屈服力与温度的相关性曲线 （如图6），拟合公式和拟合参数如表11。

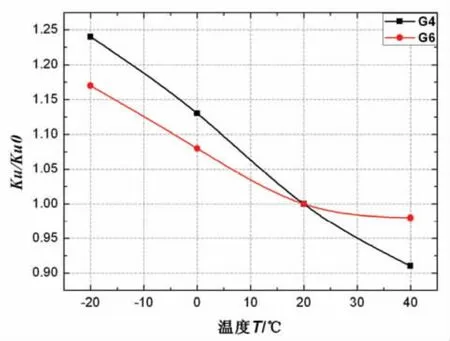
图5 屈服后刚度与温度的相关性曲线图Fig.5 Correlation curve of yielded stiffness and temperature

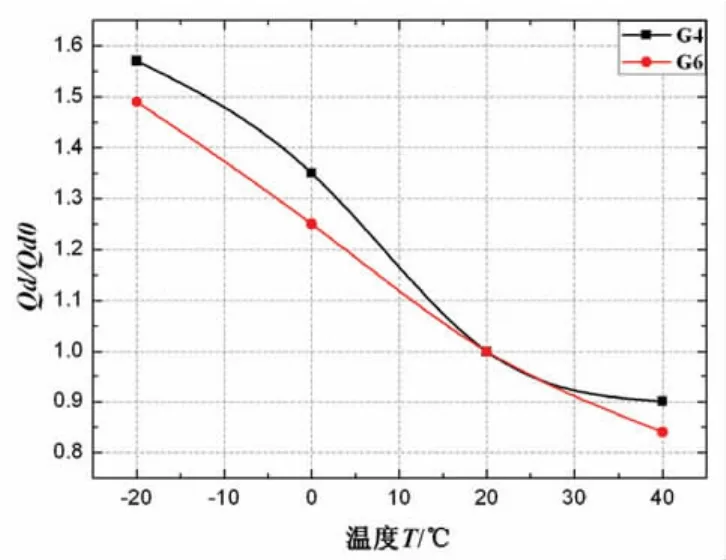
图6 屈服力与温度的相关性曲线图Fig.6 Correlation curve of yielding strength and temperature

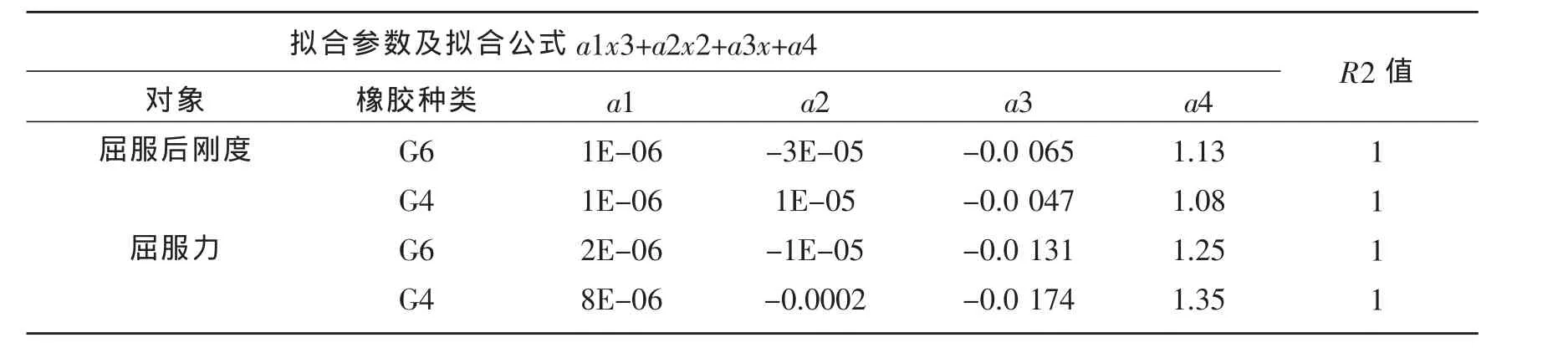
表11 屈服后刚度、屈服力与温度的相关性计算公式表Table 11 Formulae to the correlation of yielded stiffness,yielding strength and temperature

2.4 加载频率相关性

提取文献 ［2］［3］［6］中有关铅芯橡胶支座恢复力模型中水平刚度与加载频率的相关性试验数据，进行归一化处理，取均值，得到水平刚度与加载频率的相关性在试验数据点上的修正系数 （分别如12所示）。

表12 水平刚度与加载频率相关性修正系数表Table 12 Correction parameters of the correlation of the level stiffness and load frequency

2.5 60年刚度硬化相关性

根据文献 ［4］，铅芯橡胶支座等效60年刚度硬化后，测得的屈服后刚度为老化前的1.06倍。加载频率和使用年限对模型的影响可以按线性插值进行取值。

3 恢复力模型修正系数使用方法

通过以上表格中数据，可以得到各种不同使用条件下支座恢复力模型的综合修正系数。根据表3，先计算出剪切变形修正系数，然后根据表4考虑压应力的影响，再依次计算出温度和加载频率的影响，最后把各系数依次相乘，就可以得到综合修正系数，如表13所示。表中使用条件一可表示广州高层隔震结构经遇罕遇烈度的情形，使用条件二可表示哈尔滨低层隔震结构经遇多遇烈度的情形。可以看出综合修正系数与常规使用条件 “1”相比差别很大，特别是在高温大震屈服后刚度的修正系数降低到0.66（此时隔震层将趋于不安全）；在低温小震屈服后刚度的修正系数增加到1.68（此时将激起结构高阶振型，影响居住的舒适性）。由此可见，对于隔震结构的设计和分析，需要考虑当地的具体使用条件，对橡胶恢复力模型进行修正。

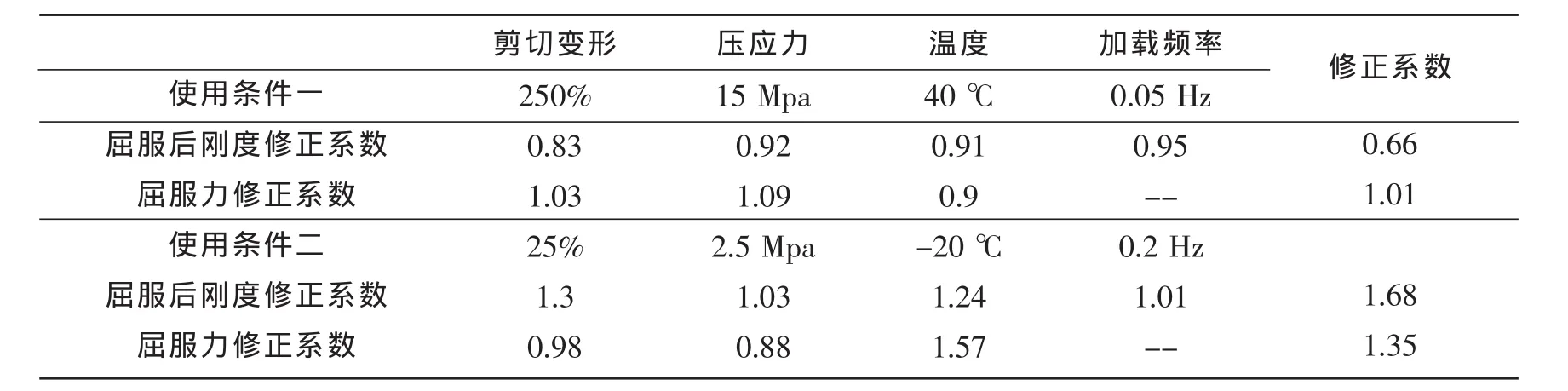
表13 不同条件下修正系数综合值Table 13 Integrated correction parrameters with different conditions

4 结论

本文通过综合有关铅芯橡胶支座的恢复力特性研究成果，分析和总结了剪切变形、压应力、加载频率和温度等因素对支座水平向恢复力模型的影响，得出了一些有益的结论。

（1）对铅芯橡胶支座的多因素影响进行了解耦分析，对试验结果进行了归一化处理，得出了在试验数据点上的修正系数；然后根据此修正系数采用四次样条曲线进行拟合，给出了拟合公式和拟合图形，提出了在各种不同使用条件下的模型修正系数，可供隔震结构的设计和分析参考使用。

（2）剪切变形、压应力和温度对屈服后刚度影响较大，加载频率和使用年限对水平刚度也有一定的影响；压应力和温度对屈服力的影响较大，但剪切变形对屈服力的影响较小；

（3）对于隔震结构的设计和分析需要综合考虑各种相关因素的影响，特别是对于一些偏离常规使用条件的隔震结构更应该如此。

［1］GB50011-2001,建筑抗震设计规范 ［S］.北京：中国建筑工业出版社，2010.

［2］刘文光,周福霖,庄学真,等.大直径夹层橡胶隔震装置力学性能试验研究 ［J］.世界地震工程,1999,15（1）： 62-68.

［3］刘文光,庄学真,林佳.夹层橡胶隔震支座长期力学性能及耐火性能试验研究 ［J］.华南建设学院西院学报,2000,8 （3） :1-10.

［4］刘文光,李峥嵘,周福霖,等.低硬度橡胶隔震支座各种相关性及老化徐变特性 ［J］.地震工程与工程振动,2002,22 （2） :115-121.

［5］刘文光,杨巧荣,周福霖.建筑用铅芯橡胶隔震支座温度性能研究 ［J］.世界地震工程,2003,19（2）:40-44.

［6］日本建筑学会著.刘文光译.隔震结构设计 ［M］.北京:地震出版社,2006.

Analysis of Decoupling to Multi-factor Role of LRB Resilience Model

ZHONG Xianfeng1，LIU Wenguang2

(1.Guangzhou University,Guangdong,Guangzhou 510006,China;2.Shanghai University,Shanghai 200072,China)

Combined with the LRB mechanical properties,many factors on the bearing horizontal restoring force model were taken into account.The paper proposed the correction parameters of the main influence factors.Then the paper decoupled bearing model.The results can be applied to existed common LRB resilience of the model.

LRB;Resilience model;Multi-factor coupling;Decoupling

P315.91

A

1001-8662（2011）02-0094-09

2011-01-14

钟先锋，男，1982年生，硕士研究生.从事工程减震研究.E-mail：zxf2008@126.com.