卡尔曼滤波器在海马场电位ripple节律分析中的应用
张 栌, 林龙年
(华东师范大学 脑功能基因组学教育部、上海市重点实验室,上海 200062)
卡尔曼滤波器在海马场电位ripple节律分析中的应用
张 栌, 林龙年
(华东师范大学 脑功能基因组学教育部、上海市重点实验室,上海 200062)
利用自适应自回归(adaptive autoregressive,AAR)模型和卡尔曼滤波器算法,分析小鼠海马CA1区场电位ripple高频振荡的时频特性.研究发现,与传统的基于短时傅立叶变换的实时频谱分析方法相比,利用AAR模型以及卡尔曼滤波器算法的参数化方法在对ripple高频振荡信号进行实时频谱分析时,具有更高的时域和频域分辨率.因此,基于卡尔曼滤波器得到的ripple能量变化,可更为准确、实时地反映ripple高频振荡的发生与变化过程.
卡尔曼滤波器; 海马CA1区; ripple; 实时频谱分析
0 引 言
在中枢神经系统中记录到的局部场电位活动,具有多种行为相关性的节律性振荡,而在大脑的海马结构中,这些节律性振荡尤为明显.在大鼠海马一般可记录到4种脑电(EEG)节律振荡,按频段依次为theta节律(4~12 Hz)、beta节律(12~30 Hz)、gamma节律(30~100 Hz)和ripple节律(100~200 Hz)[1].这些节律性电活动随着动物行为状态的不同而强弱交替,构成了一种动态平衡.当动物处于行走、探索状态以及快波睡眠时,场电位(local field potential,LFP)呈现出大幅度且有规律的theta振荡并且伴随着gamma节律;而当动物处于慢波睡眠(slow wave sleep)、安静站立等状态时,在海马CA1区则可记录到高频(120~200 Hz)的场电位振荡[2,3].这样的高频场电位节律振荡被称作ripple,一般在海马CA1区的锥体层幅度最大.在功能上,ripple高频节律被认为与记忆的巩固过程有关.最新的研究发现,海马中存在大量的位置细胞,一个位置细胞会在动物接近或穿过某一特定位置的时候增强活动,因此新环境中的空间信息由位置细胞的活动状态所表征[4],而具有相交或相邻位置域的多个位置细胞,会出现放电的相关性以及有序性,这种关系在动物慢波睡眠阶段可以重现,尤其在ripple节律发生的时候[5-8].每个ripple的时程为50~100 ms,而一系列位置细胞的有序放电又在如此短的时间内重演,因此ripple的精确侦测以及对其动力学变化的分析,对于进一步理解与研究海马多个神经元在记忆巩固时期编码的机制有着重要的意义.实时频谱分析可以同时给出时间序列信号在时域与频域的动力学描述,因此,可以作为研究ripple高频振荡及其他场电位节律的有力工具.传统的时频谱分析方法为谱图(spectrogram),即将信号分做很多重叠的时段,对每个时段分别应用短时傅立叶变换(short-time Fourier transform,STFT).其原理在于傅立叶变换将信号放到一个以正弦与余弦函数为基函数的空间,而这些基函数彼此正交,于是将原信号分解成不同频率成分.但这种方法却面临着如何在时域与频域分辨率上的协调问题(不确定性原理)[9].因为提高时间分辨率则必然导致低频率分辨率,反之亦然.而应用自适应自回归模型(adaptive autoregressive(AAR)model)来描述信号,则可以得到更高的频域分辨率.再应用卡尔曼滤波器算法来构建AAR模型进行实时频谱分析[10-13],则可进一步在保持频域高分辨率的同时,得到与信号采样频率一样精度的时间分辨率,且无需像STFT一样提取大量数据以得到自相关序列.本文运用卡尔曼滤波算法,对海马CA1场电位的ripple高频振荡进行实时频谱分析,并与传统的基于STFT的实时频谱分析方法进行比较.
1 方 法
1.1 功率谱密度
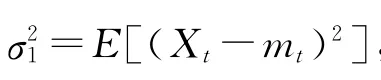
根据Cramer、Kolmogoroff和 Wiener等人的结果[14,15],协方差稳定序列的自协方差可以表示为
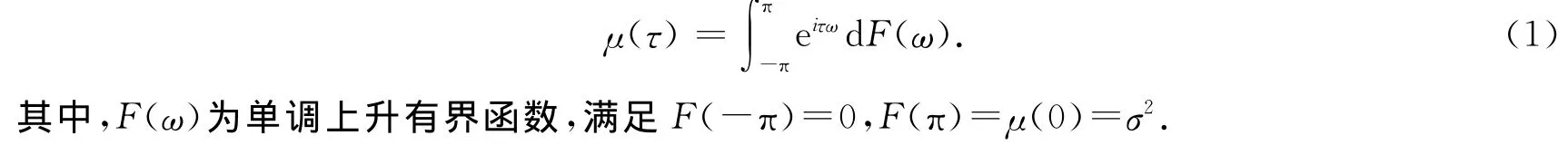
式(1)为自协方差函数的频率表示,F(ω)为频谱分布函数.如果Xt为非确定性序列(即不可被过去已知值所准确预测),则有dF(ω)=f(ω).f(ω)绝对连续,被称作是功率谱密度.f(ω)dω刻画了信号在(ω,ω+dω)频段对整个信号方差的贡献.因此,f(ω)出现某个峰值的时候,意味着该信号的相应频段可能非常重要.
记Xt的阶数m的自回归(AR)模型为

其中E(t)为时不相关偏差,其协方差矩阵为∑.
在方程两端使用傅利叶变换(Fourier transform),可以得到
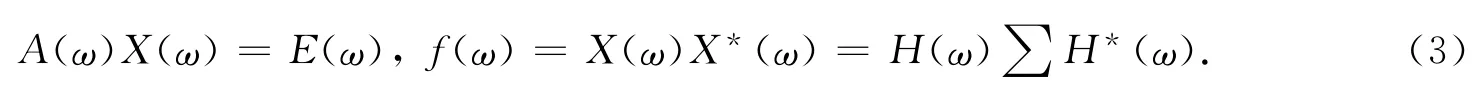
其中,H(ω)=A-1(ω)为传递函数,*为共轭转制.
1.2 自回归模型各参数的确立
自回归(AR)模型(2)中,右乘Xt-k,其中k=1,2,…,m,然后在两端取期望,于是得到Yule-Walker方程

其中,μ(q)=〈XtXt+q〉为时间延迟q的协方差矩阵.
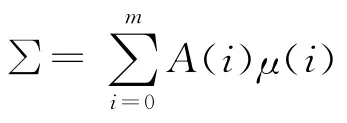
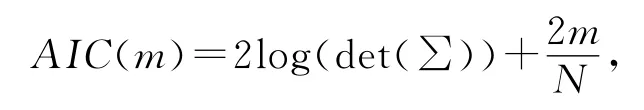
其中N为样本数.
1.3 自适应自回归模型和卡尔曼滤波器
注意AR模型(2)中的系数Ak是独立于时间的,当应用在场电位的theta振荡中时是合适的,因为theta振荡持续时间长且是连续性的,往往在10 s以上.但当应用于转瞬性很强的ripple振荡的时候,就会出现问题.这是因为ripple往往发生在大幅尖波之上,而这些尖波的突然产生与维持并没有连续性,ripple持续的时间往往只有50~100 ms,模型所要求的平稳性条件往往达不到.在这种情况下,有必要考虑随时间变化的模型参数.于是考虑如下自适应自回归模型(AAR)模型,

其中,E(t)为零均值高斯噪声过程,方差为∑t,此模型与自回归模型(2)的根本区别在于前者的模型参数随时间变化而变化.
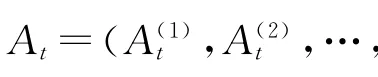
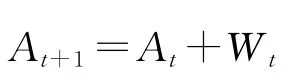
在不给出证明的情况下,这里给出卡尔曼滤波器方程如下,其理论推导的细节详见文献[12].

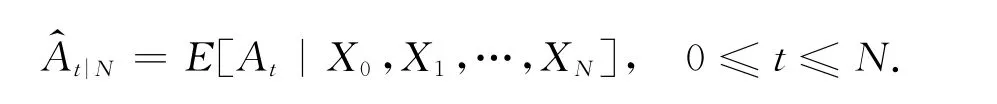
这样的估计更加光滑,也被称作平滑器(smoother).据此可以得到新的参数估计[19],

2 结 果
2.1 不同行为状态下小鼠海马CA1区场电位的基本特征
对不同行为状态下,小鼠海马CA1区记录到的场电位进行功率谱密度分析,结果显示,在探索活动以及REM睡眠状态下,场电位表现出规律的theta节律振荡,同时在theta波峰处,出现gamma节律快速振荡(见图1A和C).另外,在REM睡眠状态下记录到的theta节律相对更为规则(见图1C).而在动物探索活动的时候,一般还有伴有beta节律(见图1A).在慢波睡眠状态,则以在大幅尖波上出现的ripple节律高频振荡为主 (见图1B).
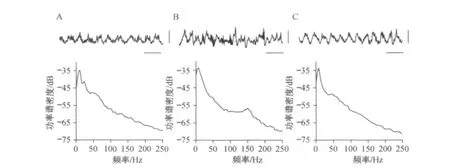
图1 海马CA1区场电位及其功率谱密度分布Fig.1 LFP signals recorded in hippocampal CA1 and power spectral density disctribution
2.2 基于卡尔曼滤波器的实时频谱分析对ripple的侦测
实时频谱分析可以准确地描述场电位ripple高频频段的发生以及在频域的动态变化,当ripple发生时,在100~200 Hz的频域上可以看到能量相应增强(见图2 B和C).本文对传统的基于短时傅立叶变换(STFT)的谱图(spectrogram)(见图2B)以及基于卡尔曼滤波器算法的实时频谱分析图进行了对比分析(见图2C).对比相应的原始场电位(见图2A),可以发现基于卡尔曼滤波器算法的实时频谱分析在频域以及时域上具有更高的分辨率.同时,传统的基于短时傅立叶变换(STFT)的谱图由于必须对信号进行分段加窗处理(此处为50 ms的hanning窗,1 ms的时间步长),并采用时间窗中的中位时间作为该窗的时刻对应点因此,因此对ripple波的侦测有一个开始时的时间提前量和结束时的时间延迟量.而卡尔曼滤波器本身是AAR模型的一种以采样时间为时间步长的自适应迭代算法,再应用平滑器对迭代进行修正,从而在侦测ripple波时,开始的时间提前量以及结束的时间延迟量均很小.
为了进一步定量比较这两种方法对ripple波侦测准确性的差异,将每个时间点ripple段的能量求和,作为ripple能量随时间变化的表示(见图3C).同样的,基于SFFT的实时频谱分析也可以得到ripple能量随时间的变化过程(见图3D).将得到的这两组ripple能量变化曲线,分别与场电位ripple滤波信号(见图3B细线)的幅度(见图3B粗线)相比较,从而得到两组相关系数ρAAR与ρSFFT.由于ripple节律随时间的强弱变化可以由场电位ripple滤波信号的幅度(见图3B粗线)进行描述,因此该相关系数越接近1,说明相应的实时频谱分析越能准确表达场电位ripple段的能量变化.
10组不同小鼠的场电位记录(每组3段,各5 s时长)数据分析显示,ρAAR(mean=0.677,median=0.708)高于ρSFFT(mean=0.630,median=0.671),(见图4A,p≪0.001,Wilcoxon signed rank test).相关系数指数(见图4B)亦显示ρAAR>ρSFFT(p≪0.001,Student test).以上结果表明,基于ARR模型的实时频谱分析在侦测场电位ripple段的能量变化时,较STFT方法更为精确.
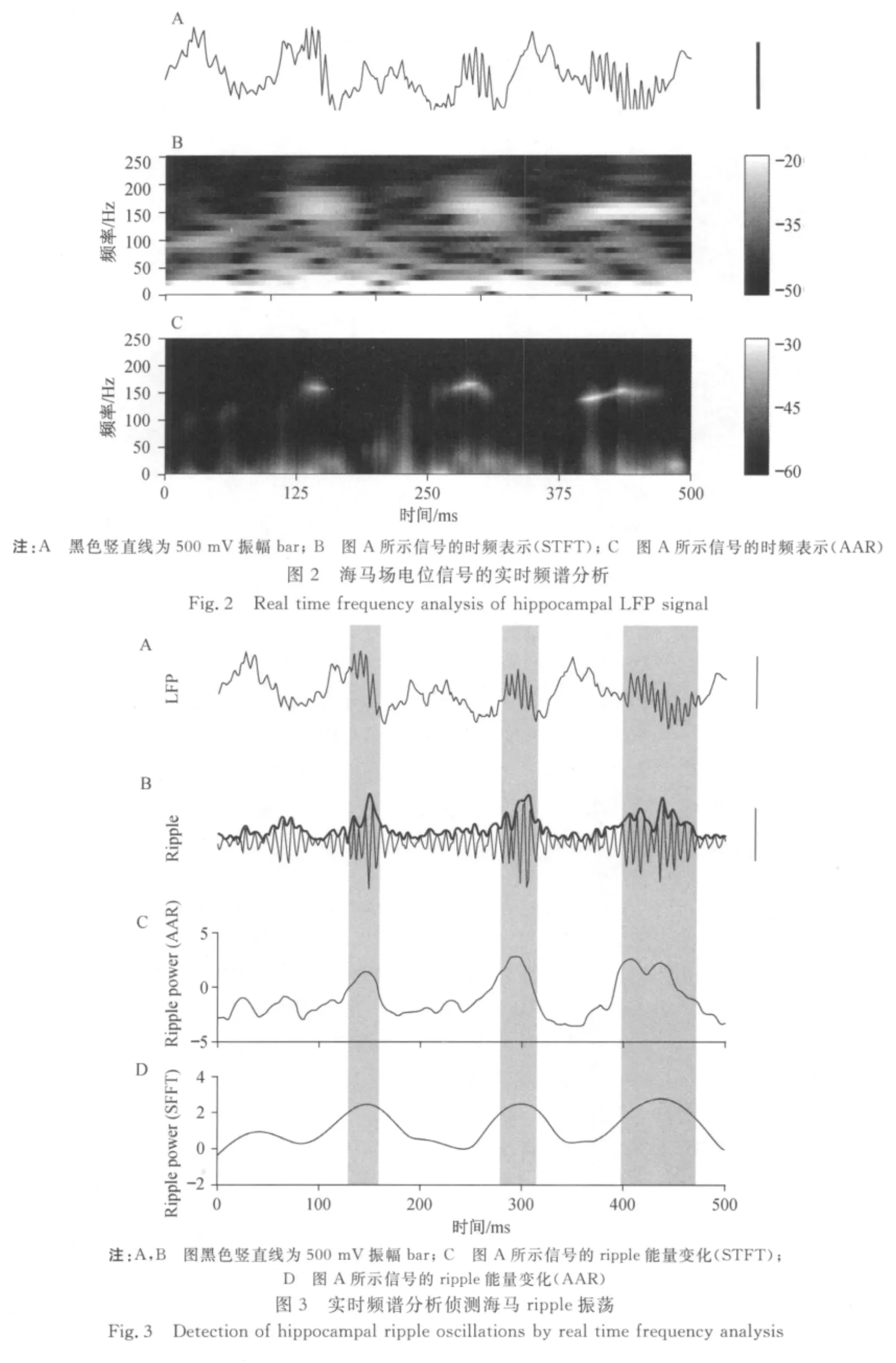
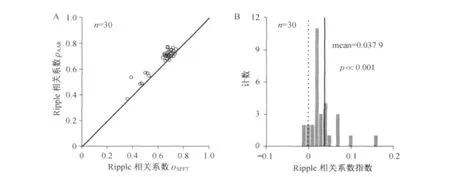
图4 STFT方法与卡尔曼滤波器方法侦测ripple振荡的效果比较Fig.4 Compartment of ripple detection through STFT and Kalman filter
3 讨 论
AAR模型及卡尔曼滤波器算法中涉及到许多参数的设置.首先,AAR模型应用于非平稳序列的阶数,不同于AR模型对平稳序列可以利用AIC等准则进行确定[13].其次,模型描述数据的准确性受到状态更新噪音为以及观测噪音的影响,而卡尔曼滤波器是一个迭代算法,因此各参数的初始值的不同设置将影响到模型估计的结果.对于此,并没有完整的解决方案[13,20,21],参考已有的研究工作,以及考虑到场电位数据本身的特性,我们将模型阶数p设为9;初始观测噪音为0.001,初始状态更新噪音为0.000 1.
研究结果显示,基于STFT的实时频谱分析,无法在时域和频域同时高精度地表示场电位的ripple节律.而基于ARR模型以及卡尔曼滤波器算法得到的信号实时频谱分析,提供了一个比传统STFT更为有力的工具.该法在脑电(EEG)的分析方法中已有一些应用[22,23],而平滑器的应用不但让得到的频谱更加光滑,而且消除了对信号表征的时间延迟[13];另一方面,平滑器是基于信号的离线分析为前提,当进行信号的在线解码时,便无法应用.Wilson的研究小组,基于二阶ARR模型与卡尔曼滤波器的算法,侦测海马区场电位ripple信号的发生与起始,得到了比传统的运用ripple滤波信号的幅度(通过希尔伯特变换)侦测方法更好的效果[21].而我们将原始场电位直接用ARR模型直接描述,由此可以得到被Nyquist frequency限制的大范围的频谱,更准确地描述了场电位ripple频段频率以及能量大小的变化.
AR模型同ARR模型一样也是参数化方法,但前者中各个参数不随时间变化而变化,并要求信号是平稳信号.一般认为12 s以上的EEG信号是平稳的[24],而发生在尖波之上持续时间仅为50~100 ms的ripple信号则难以达到这一要求.对于低频的theta振荡,由于其持续时间较长(往往达到数十秒以上),而且其节律振荡的子周期也在120 ms左右.因此不但可以应用AR模型来进行实时频谱分析,传统的SFFT也可以应用较大的时间窗来得到较高的频域分辨率,从而使方法不同造成的相对较低的时间分辨率可以被忽略.
[1] ANDERSEN P.The Hippocampus Book[M].Oxford:Oxford University Press,2007.
[2] BUZSAKI G,HORVATH Z,URIOSTE R,et al.High-frequency network oscillation in the hippocampus[J].Science,1992,256:1025-1027.
[3] O′KEEFE J,NADEL L.The Hippocampus as a Cognitive Map[M].Oxford:Clarendon Press,1978.
[4] O′KEEFE J,DOSTROYSKY J.The hippocampus as a spatial map.Preliminary evidence from unit activity in the freely-moving rat[J].Brain Res,1971,34:171-175.
[5] WILSON M A,MCNAUGHTON B L.Reactivation of hippocampal ensemble memories during sleep[J].Science,1994,265:676-679.
[6] LEE A K,WILSON M A.Memory of sequential experience in the hippocampus during slow wave sleep[J].Neuron,2002,36:1183-1194.
[7] FOSTER D J,WILSON M A.Reverse replay of behavioural sequences in hippocampal place cells during the awake state[J].Nature,2006,440:680-683.
[8] O'NEILL J,SENIOR T J,ALLEN K,et al.Reactivation of experience-dependent cell assembly patterns in the hippocampus[J].Nat Neurosci,2008(11):209-215.
[9] BENEDICKS M.On fourier transforms of functions supported on sets of finite Lebesgue measure[J].Journal of Mathematical Analysis and Applications,1985,106:180-183.
[10] KALMAN R E.A new approach to linear filtering and prediction problems[J].Transactions of the ASME,1960:35-45.
[11] KALMAN R E,BUCY R S.New results in linear filtering and prediction theory[J].Transactions of the ASME Series D,Journal of Basic Engineering,1961,83:95-107.
[12] ANDERSON B D O,MOORE J B.Optimal Filtering[M].New Jersey:Prentice Hall,1979.
[13] TARVAINEN M P,HILTUNEN J K,RANTA-AHO P O,et al.Estimation of nonstationary EEG with Kalman smoother approach:an application to event-related synchronization (ERS)[J].Biomedical Engineering,IEEE Transactions on,2004,51:516-524.
[14] CRAMER H.On the theory of stationary random processes[J].The Annals of Mathematics,1940,41:215-230.
[15] WIENER N.Extrapolation,Interpolation,and Smoothing of Stationary Time Series,with Engineering Applications[M].Cambridge:Technology Press of the Massachusetts Institute of Technology,1949.
[16] MORF M,VIEIRA A,LEE D T L,et al.Recursive multichannel maximum entropy spectral estimation[J].Geoscience Electronics,IEEE Transactions on,1978,16:85-94.
[17] DING M,BRESSLER S L,YANG W,et al.Short-window spectral analysis of cortical event-related potentials by adaptive multivariate autoregressive modeling:data preprocessing,model validation,and variability assessment[J].Biological Cybernetics,2000,83:35-45.
[18] AKAIKE H.A new look at the statistical model identification[J].Automatic Control,IEEE Transactions on,2003,19:716-723.
[19] HAMITON J D.Time Series Analysis[M].Princeton:Princeton University Press,1994.
[20] ALOIS S.The electroencephalogram and the adaptive autoregressive model:theory and applications[D].Technischen Universitat Graz,2000.
[21] NGUYEN D P,KLOOSTERMAN F,BARBIERI R,et al.Characterizing the dynamic frequency structure of fast oscillations in the rodent hippocampus[J].Front Integr Neurosci,2009(3):11-11.
[22] BOHLIN T.Analysis of EEG signals with changing spectra using a short-word Kalman estimator[J].Mathematical Biosciences,1977,35:221-259.
[23] AMOLD M,MILNER X H R,WITTE H,et al.Adaptive AR modeling of nonstationary time series by means of Kalman filtering[J].Biomedical Engineering,IEEE Transactions on,1998,45:553-562.
[24] COHEN B A,SANCES A.Stationarity of the human electroendephalogram[J].Med Biol Eng Comput,1977,15:513-518.
Analysis of hippocampal ripple osillations by application of Kalman filter
ZHANG Lu, LIN Long-nian
(Key Laboratory of Brain Functional Genomics,Ministry of Education and Shanghai,Institute of Brain Functional Genomics,East China Normal University,Shanghai 200062,China)
This paper studied high frequency ripple(100~200 Hz)oscillations in hippocanpal CA1 area by applications of adaptive autoregressive(AAR)model and Kalman filter.Compared with traditional real time frequency analysis of time seies based on short term Fourier transfrom(STFT),improved time and frequency resolutions in time-frequency representation could be achieved by parametric methold obtained by AAR model and Kalman filter algorithms.Thus,the occurance of ripple oscillations and the variation of ripple power could be addresed more accurate by Kalman filter than that of STFT.
Kalman filter; hippocampal CA1; ripple; real-time frequency analysis
Q6
A
10.3969/j.issn.1000-5641.2011.06.010
1000-5641(2011)06-0081-08
2010-11
上海市教育委员会科研创新项目(09ZZ44);国家自然科学基金重大项目(30990262)
张栌,男,博士研究生.E-mail:math2437@hotmail.com.
林龙年,男,教授.E-mail:lnlin@brain.ecnu.edu.cn.

