用于车辆监控系统的单目视觉二维标定新算法
王庆峰,张全法,李 焕,任朝栋
(郑州大学 物理工程学院,郑州 450001)
基于单目视觉的车辆监控系统应用的标定方法有一维标定方法和二维标定方法.由于一维标定方法仅能测量两点之间的纵向距离,只可以用来检测交通流量[1].若要通过车辆识别与跟踪技术检测各种违章行为如违章调头,则必须进行二维标定,即确定图像上的点在二维路面坐标系里的坐标.由于实际应用中需要监控的路口或路段很多,不同路口或路段的监控区域在形状、大小等方面各不相同,而监控范围又非常大,导致标定参照物的制作、运输和摆放等都存在困难,那些应用于其他领域、需要特制标定参照物的小范围标定算法是不适用的[2-5].文献[6]介绍的二维标定算法通过自动识别高速公路车行道分界线来推导云台摄像机的参数,虽然不需要特制的标定参照物,但是不适用于非结构化的城市道路,而且仍然需要通过复杂的算法来确定摄像机参数,具有很难保证解的唯一性和稳定性、受图像噪声影响大等缺点.为此,本文提出一种新的二维标定算法,不需要特制的标定参照物,也不需要确定摄像机参数,既适用于城市道路,又具有算法简单、操作方便、标定范围大、标定速度快等特点,在实际应用中获得了较好的效果.
1 标定算法
为了方便讨论,利用一幅在交通路口拍摄的图像建立图像坐标系OXY和路面坐标系oxy,如图1所示.OXY为平面直角坐标系,任意像素在其中的坐标用(X,Y)表示.oxy近似为平面直角坐标系,因为一般情况下监控区域可以近似为平面,任意像素在其中的坐标用(x,y)表示.这里取y轴与一条车行道分界线重合,x轴与之垂直.假定摄像机的光轴与x轴垂直,并且X轴与x轴平行.

图1 图像坐标系和路面坐标系
1.1 变量分离
根据成像原理推导 x、y与X、Y的关系时,x、y皆为X、Y的二元非线性函数,而且包含难以确定的摄像机内部、外部参数[7].为此,基于针孔成像模型在图1中绘制了几条直线,它们在路面坐标系里的关系为:os、gr、fd 、ac 四者相互平行 ,os、gr 之间的距离等于fd、ac之间的距离,并且都等于人行横道线宽度;bt、cs类似于ao,也分别与车行道分界线重合,三者相互平行,并且ao、bt之间的距离等于bt、cs之间的距离.通过观察它们在图像坐标系里的位置,发现利用变量分离法可以简化这种关系.
首先,Y坐标相同的像素的y坐标也相同,而Y坐标不同的像素所代表的y方向增量dy不同.因此可用一个与X无关的非线性函数y=f(Y)来描述各像素的y坐标与Y坐标之间的关系.f(Y)为Y的非线性函数这种关系,是由成像原理造成的.
其次,X坐标相同的像素的x坐标一般不同,X坐标不同的像素的x坐标可能相同,而Y坐标不同的像素所代表的x方向增量dx不同.这使得可以用一个与Y无关的非线性函数x=fM(X)来描述Y坐标为M的像素行上各像素的x坐标与X坐标之间的关系,其中M=0,1,…,N-1,N 为图像Y 轴方向像素数.M必须有N个不同的取值,否则无法实现 fM(X)的变量分离,从而不利于求解x.fM(X)并非必须为X的非线性函数,因为在针孔成像模型下Y坐标相同的像素所代表的dx相同,采用非线性函数是为了在一定程度上弥补这种模型忽略镜头畸变的不足.
1.2 多项式逼近
根据级数理论,无论非线性函数y=f(Y)多么复杂,当|Y|<1时都可以用下面的多项式来逼近它:
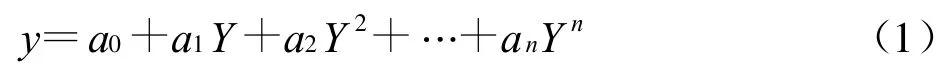
式中:n为多项式阶数;a0,a1,…,an为待定系数,当摄像机调试好后为常数,可以通过标定确定,相对于通过标定确定摄像机内部、外部参数来说要简单得多.
一般情况下,增大n有利于提高逼近精度.但是n越大,待定系数越多,所需标定数据也越多,标定操作也越复杂.考虑到测量车辆位置时引起误差的主要因素是车身高度与阴影等,太高的逼近精度意义不大,所以n不必取得很大.通过尝试和比较,发现取n=3即可满足要求.此时式(1)变为:
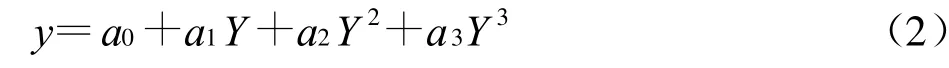
确定式(2)中各待定系数的方法有最小二乘法、神经网络法和解方程组法等.前2种方法都需要m>4组标定数据,并且m越大越有利于减小标定数据之误差的影响,但是标定操作也越复杂.由于标定误差不是测量误差的主要来源,并且标定数据时可以比较精确地人工测量图像上两点之间的实际距离,从而使标定数据的误差比较小,所以采用第三种方法,此时只需要m=4组标定数据.实验证明,这样做能够满足要求.
假设有 4组标定数据(yi,Yi),i=1 ,2,3,4,代入式(2)可得关于 a0,a1,…,an的线性方程组 :
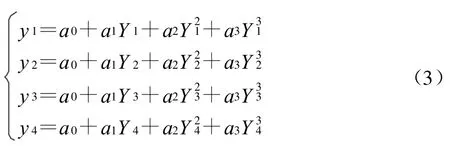
利用程序求解方程组(3)很容易,不再赘述.而一旦解得 a0,a1,…,an,即可利用式(2)由图像坐标系里的Y坐标求取路面坐标系里的y坐标.若摄像机参数发生了变化,重新进行标定也很方便.
至于 x=fM(X)的确定,与上述过程类似,只不过对于每个M,都需要m=4组标定数据.
1.3 利用交通标线进行标定
根据上述分析可知,只要知道了4个像素的Y坐标与y坐标,就可以通过求解线性方程组确定 f(Y);而要确定 fM(X),则需要在每行像素上都知道4个像素的X坐标与x坐标.这正好可以利用交通标线来解决.利用人行横道线、虚车行道分界线等可确定f(Y),因为给定它们的端点到 x轴距离的人工测量值后,这些点的y坐标与Y坐标皆属已知.利用平行于y轴的车行道分界线与车行道边缘线等可确定fM(X),因为给定它们到y轴距离的人工测量值后,其上所有像素的x坐标皆属已知、X坐标皆属可求.不过为了提高确定各种交通标线的可靠性,应采用人工指定的方法而不采用文献[8]介绍的自动识别法,因为城市道路上车行道分界线可能不是直线并且虚实不定,车行道分界线间距与人行横道线宽度不是常数,各种交通标线可能残缺不全,及其他原因.
1.4 标定过程
在图像上利用交通标线绘制坐标系之后,确定f(Y)的过程如下:
(1)在图像上利用交通标线绘制3条与x轴平行、到x轴距离不为0且各不相同的直线,以便调整其上下位置.调整好后,输入它们到 x轴距离的人工测量值即3个y值,由程序根据它们在图像坐标系里的位置求出3个Y值.再根据x轴在图像坐标系里的位置求出第4个Y值,而其y值为0.于是得到4组标定数据.
(2)取Ymax为稍大于|Yi|中最大值的数的整数,将Yi/Ymax作为新的Yi,实现对标定数据Yi的归一化,i=1 ,2 ,3 ,4.
(3)将归一化后的标定数据代入式(3),解方程组得到 aj,j=0 ,1 ,2 ,3.
(4)进行反归一化,将 aj/Yjmax作为待定系数aj,j=0 ,1 ,2 ,3.
确定 fM(X)的过程与上述过程的主要区别在于:需要在图像上利用交通标线绘制3条到y轴距离不为0且各不相同的直线,并且仔细调整它们的端点,使其在路面坐标系里与y轴平行;还需要输入它们到y轴距离的人工测量值即3个x值.对于每行像素,皆需由程序根据所绘直线在图像坐标系里的方程求出3个X值,并根据y轴在图像坐标系里的方程求出x=0的像素的X坐标即第4个X值,而第4个 x的值为0,从而得到4组标定数据.对于每行像素,皆需解方程组,所得待定系数各不相同.
2 实验结果及分析
利用型号为SONYH3的数码相机拍摄了一段AVI格式的视频用于实验,图像大小为640×480像素,相机高度约170cm.所用计算机的CPU为Pentium系列处理器,主频1.70GHz;程序用VC6.0编写.路面坐标系如图 2所示.用于确定 f(Y)的3条纵向标定线如图3所示,用卷尺测得它们到 x轴的距离分别为 300cm 、600cm、920cm.用于确定 fM(X)的3条横向标定线如图4所示,用卷尺测得它们到y轴的距离分别为140cm、300cm、400cm.需要说明的是,程序中绘制各种线条时,线条宽度仅1个像素;为了便于观察,这里把线条描绘成了较粗的形状.若不考虑界面操作耗时,纵向、横向标定耗时均在1s之内,非常快.


图4 横向标定线
为了评价标定精度,在不同位置设置标识物,用卷尺测量其路面坐标的实际值,将鼠标移动到标识物上,由程序根据鼠标在图像上的位置计算路面坐标的测量值,结果如表1所示.表1中ex、ey分别表示横向、纵向相对误差.可以看出,标定精度能够满足实际应用的要求.
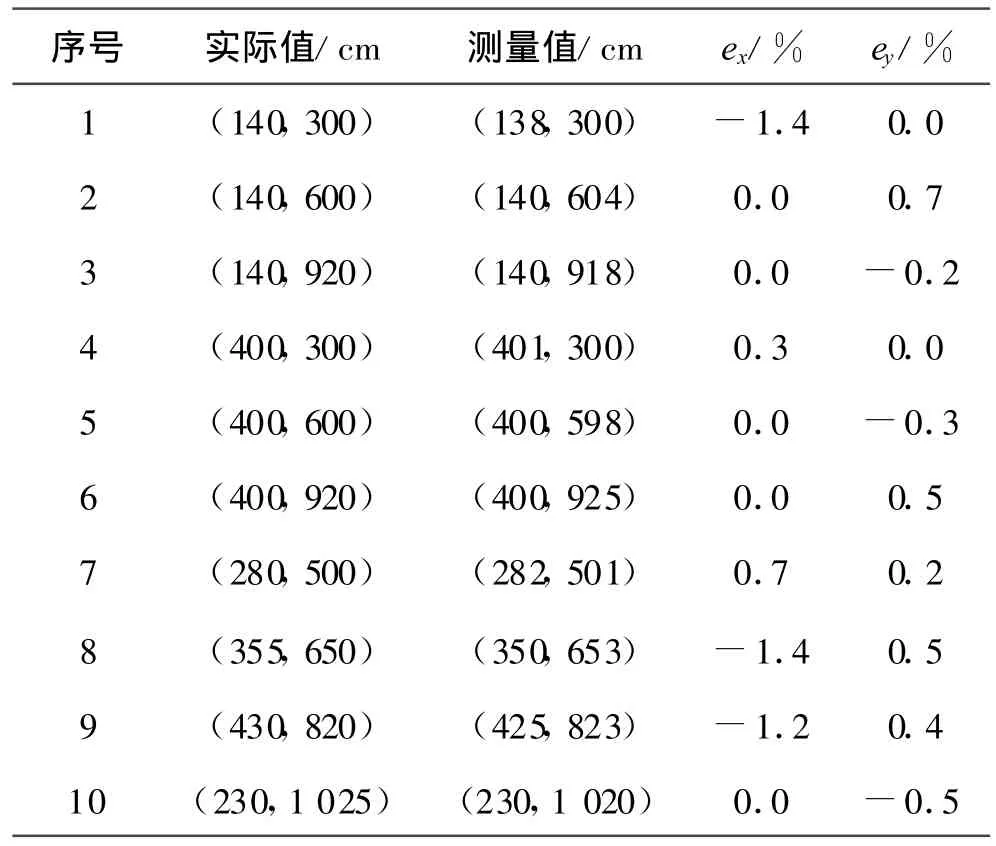
表1 路面坐标测量结果
在设计的车辆监控系统中应用了上述标定算法.该系统首先对二值化的背景差分图像进行车辆识别,再进行交通参数计算和违章判定等.对于识别出的车辆,它可以给出其在路面坐标系或图像坐标系里占据的矩形区域,分别如图 5、图 6所示(图像经过了裁剪).若未经标定,在图像坐标系里欲求取图6所示矩形很容易,欲求取图5所示四边形(在路面坐标系中为矩形)却很困难,因为必须对车辆轮廓数据进行大量的复杂运算.而经二维标定后,在路面坐标系里求取图5所示矩形则非常容易.显然,由图5所示矩形确定车辆的位置,要比根据图6所示矩形确定车辆的位置更为准确.另外,若不进行二维标定,也无法比较不同位置车辆的大小和左右关系.

不过,仅根据标定结果对交通参数与违章行为进行非常准确的计算与判定尚存在一定的困难,其中主要原因在于车身、底盘高度及车身、底盘阴影的影响,需要采取进一步的措施.例如,估计车速时,根据车辆离摄像机最近端的位置,并采用文献[9]中的方法,在消除阴影时保留车辆底部的暗影来减小底盘高度的影响(如图5所示);检测是否越过中心黄色双实线时,将摄像机安装到其上方,并使其图像尽量与Y轴平行.
3 结 语
利用单目视觉二维标定算法可以对车辆监控系统进行二维标定,从而可以通过车辆跟踪实现各种违章判定.这种算法利用了监控现场广泛存在的交通标线作为标定参照物,通过求解线性方程组建立路面坐标与图像坐标之间的关系来避免求取摄像机参数,具有标定速度快、标定范围大、操作方便、算法简单、标定精度高等特点.将这种算法应用到设计的车辆监控系统,在现场测试中获得了较好的效果.
[1]张洁颖,王生进,丁晓青.基于视频图像处理的交通流检测系统[J].电视技术,2008,32(6):68-70.
[2]谢勇辉,王从军,黄树槐.实现计算机视觉标定自动化的一种新技术[J].华中科技大学学报(自然科学版),2004,32(8):13-15.
[3]李良福,陈卫东,冯祖仁,等.目标跟踪与定位中的视觉标定算法研究[J].应用光学,2008,29(4):481-487.
[4]李小峰,李峰.单目摄像机标定方法的研究[J].计算机工程与应用,2009,45(15):229-232.
[5]王蓓蓓,王向军,张召才.基于虚拟直线的单目视觉坐标测量模型研究[J].传感器与微系统,2009,28(10):20-22.
[6]李勃,陈启美.基于监控视频的运动车辆行为分析算法[J].仪器仪表学报,2006,27(s3):2118-2120.
[7]邱茂林,马颂德,李毅.计算机视觉中摄像机定标综述[J].自动化学报,2000,26(1):43-55.
[8]杨喜宁,段建民,高德芝,等.基于改进 Hough变换的车道线检测技术[J].计算机测量与控制,2010,18(2):292-294.
[9]任朝栋,张全法,李焕,等.快速消除车辆阴影的多阈值图像分割法[J].应用光学,2010,31(6):961-964.

