一种基于种子生长的匹配算法

贺 亮， 刘 荣， 吕开云

(东华理工大学测绘工程学院，江西抚州 344000)

一种基于种子生长的匹配算法

贺 亮， 刘 荣， 吕开云

(东华理工大学测绘工程学院，江西抚州 344000)

立体匹配是三维重建的重要组成部分，被广泛用于数字城市、虚拟现实等领域中。提出了一种基于种子生长的匹配点扩散算法。首先用SIFT算法提取图像间对应的特征点并将其做为种子点，对种子点在其领域范围进行区域传播匹配。接着将生长得到稠密匹配点经重采样转换为准稠密匹配点。最后再用对称对极点距离法去除误匹配得到整幅图像上均匀分布的精确匹配点对。实验表明，改进的算法对于表面结构重复性高、未校正的图像均适用并能得到较好结果。

SIFT算法;区域传播;极线校正;准稠密匹配

立体匹配是三维重建的关键技术之一，通过恢复立体像对所对应匹配点的空间三维坐标及三维网格连接和纹理映射可以完成三维物体可见表面的几何结构(张祖勋等，1997)。随着三维重建在数字地球、数字城市和虚拟现实等领域应用的发展，立体匹配技术也越来越受到广大研究人员的关注。然而，图像对应点自动匹配的密度及精度间并没有得到很好的解决。

立体匹配的算法研究分为全局算法和局域算法两大类(陈鹰，2003)。全局算法主要是通过优化某一视差函数来完成，如傅立叶变换的方法。该算法的不足之处是计算时间较长，难以满足实时重建的要求。局域算法又可分为基于特征的匹配算法和基于像素的匹配算法。基于特征的匹配能够通过Harris，SIFT，MSER等匹配方法准确提取图像的特征，降低了时间和空间复杂度，但只能得到少数的匹配基元，远远无法满足三维物体精准可视化的要求。基于像素的匹配方法则是对每一个像素都计算一次匹配，虽然能得到稠密的匹配点集，但十分耗时且可靠性不高。

针对上述各匹配方法存在的缺陷，有研究人员提出了种子生长的匹配方法(Ottog et al.，1989)。稠密匹配的各种方法也孕育而出。本文根据稠密匹配的原理，简化了Lhuillier等(2005)中的算法，提出了一种新的稠密匹配方法，先使用SIFT算法提取出可靠性较高的特征匹配点做为种子点，接着使用Best－First原则从匹配点集中找出最可靠的点对，对其进行区域传播稠密匹配得到稠密的匹配点集。考虑到所有匹配点是用于三维重建的，在得到的点集中使用重采样的方法得到均匀分布的准稠密点，最后再用对称对极点距离法消除误匹配，通过三维网格的建立及纹理映射，得到满足视觉要求的三维物体重建。

1 SIFT特征基元的提取与匹配

点特征是影像最基本的特征，常被用于图像的配准与匹配，目标描述与识别和立体像对3D建模等众多领域(官云兰等，2007)。SIFT特征(Scaleinvariant feature transform，尺度不变特征转换)是一种电脑视觉的算法用来侦测与描述影像中的局部性特征，它在空间尺度中寻找极值点，并提取出其位置、尺度、旋转不变量，此算法由Lowe(2005)提出。此方法是将图像分为各个子区域来计算其位置和方向的三维直方图，然后使用直方图法得到描述子，即使在图像形变的情况下仍能保持很好的稳定性(贾永红，2003)。优于常规的利用灰度相关性作依据的匹配方法。所以采用SIFT用于初始点的匹配提取。

根据SIFT算法提取出特征向量的灰度相似性作为两幅图像匹配点的相似性判别量，使用ZNCC(归一化零均值互相关系数)来建立初始匹配。ZNCC定义如下:

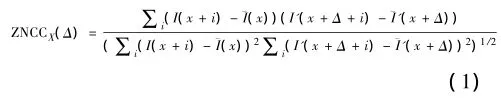
式中 Δ=(Δx，Δy)T为对应点X=(x，y)T的偏移量，¯I(x)和¯I'(x)分别为两幅图像中以x为中心的窗口内所有像素灰度的平均值。ZNCC的取值范围为－1～1，值越大则表示对应点的相似程度越高。本文中的相关性窗口取值为7，将ZNCC＞0.8的点对做为种子点。

2 匹配点扩散算法

本文中的匹配点扩散算法流程图由图1来表示。

图1 扩散算法流程图Fig.1 The flow chart of propagation algorithm

下面介绍每个步骤的详细操作:

Step1。将已得到的种子点按ZNCC值从大到小的顺序排一个队列，从队列顶端取出可靠性最高的一对种子点(Xi，X'i)，并将其在种子队列中删除。使用Best－First(最优最先)的策略，即每次都由最可靠的种子点来扩散出相应匹配点，保证了扩散出来的匹配点的精确度，从一定程度上达到了全局优化的效果。种子点的领域定义为:

种子点的领域可被表示为(2N+1)×(2N+1)的像素集，其中N为领域的半径，一般取值为2。

Step2。由以下四个约束条件在种子点的领域里扩散出满足条件的匹配点。

(1)离散二维视差梯度约束。根据物体表面一般都存在平滑性得出临近的点需满足一定的视差要求，满足其要求的匹配点定义为

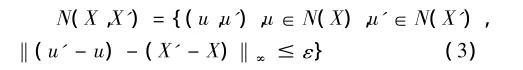
其中ε为视差梯度的阈值，可取值为1。

(2)灰度相似性约束。匹配点要求灰度的相似性达到一定程度，文中要求匹配点的ZNCC值必须大于0.5。

(3)置信度约束。置信度约束使得匹配点的扩散能沿着边缘扩散而不扩散到灰度过于一致的区域，本文中的置信度定义为:

在图像灰度归一化的情况下，文中设定扩散只在满足＞0.01的条件下进行。相似的置信度约束还有Moravec算子(Moravec，1977)。

(4)唯一性约束。根据像对匹配点需满足一一对应的原则，当Xi或X'i在对应的图像上已存在匹配点，则不再对该点进行扩散匹配。

将通过Step2得到的匹配点放入种子点队列slist中，重复Step1和Step2，直至种子队列中不再存在种子点。所有的匹配点便组成了稠密匹配点集。

Step3。由于本文中立体匹配的目的是为了三维重建，所以只需要准稠密匹配点集即可，通过重采样，可以得到均匀分布的更加准确可靠的匹配点。将第一幅图像分割成8×8的小方格区域，在方格区域内的稠密点集使用Ransac方法估算与其对应第二幅图像中小区域的仿射矩阵H，由此保证了仿射矩阵不会受到一些误匹配点的影响。计算第一幅图像个小方格区域的中心点坐标C，计算得到在另一幅图像中对应的中心点H*C。如果小方格区域中存在初始种子点，用同样方法得到对应点(图2)。将这一步中得到的所有点放入集合，组成准稠密匹配点集。由于最后得到的准稠密匹配点是各个区域的中心点通过相应的仿射转换得到的，所以即使初始种子点因纹理重复等原因匹配错误，对得到准稠密匹配点影响也有限。

图2 重采样示意图Fig.2 The resample of square grid

Step4。使用Ransac方法用8点法迭代计算出立体像对间的基本矩阵F。计算过程中使用对称对极点距离法来去除不满足条件的外点(郑碧娜等，2009)。通过设定阈值，可以除去此前因纹理重复或各种原因产生的不满足要求的匹配点，保留下来的匹配点均在一定精度以内，大大提高匹配点的准确度。

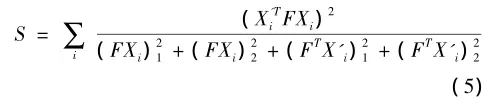
其中F为计算得到的基本矩阵;(FXi表示矢量FXi的第j个元素的平方。文中要求S＜1.0，即表明只保留下误差值在1个像素距离以内的匹配点。

3 实验结果及分析

采用文中提到的扩散算法，对两组图像(一组为校正图像，另一组为未校正图像)做了扩散及重采样的实验。实验平台为Matlab2008a，算法的主要参数设置为:ZNCC领域半径为2，扩散要求匹配点ZNCC＞0.5，视差梯度阈值取1，置信度取值0.01。

3.1 校正图像

如图3所示，图3a，图3b分别表示原始图像的左图和右图，图3c表示了左右两图的视差图，是由经Step1，Step2循环得到的稠密匹配点(共得到115 261对匹配点)对列坐标相减得到，视差图中个像素的灰度信息表示了物体距离的远近信息，灰度越大表示距离越近。从视差图上可以直观的了解到经由Step1，Step2循环得到的稠密匹配点对是比较准确的。图3d则是经过重采样和核线约束后得到的准稠密匹配点(共2 000对匹配点)。

3.2 未校正图像

如图4所示，同样在未校正像对上运用了该算法，图4a，图4b分别表示原始图像的左图和右图，由于未校正图像无法通过匹配点列坐标相减得到视差图，为了直观地表达经由Step1，Step2循环得到的稠密匹配点对(共198 716对匹配点)的准确性，采用了另一种方法来表示，如果图4a中一点与图4b中一点匹配，则将点的灰度复制到结果图像点的位置。图4c为得到的匹配效果图(黑色部分为未匹配区域)，它可以直观的表达稠密匹配的效果，图中可以看出本文中的算法在存在结构重复性较高的区域也取得了精确的结果。图4d为最后得到的准稠密匹配图(共5 094对匹配点)。

4 结论

从以上对校正图像和未校正图像的实验中可以看出，本文提到的立体匹配扩散算法对于表面结构性重复高、未校正的图像均适用并能得到较好结果。先使用SIFT算子结合ZNCC提取出初始的种子点，经由区域扩散和重采样后得到稠密的匹配点集，从实验中可得出这些稠密匹配点已具有较高精度，接着通过重采样和核线约束得到对于整幅图像均匀分布的更加准确的准稠密匹配点，在提高精度的同时也合理减少了三维重建时的数据量。恢复这些准稠密匹配点的三维坐标、建立三维网格及纹理映射之后，就可以得到逼真的可视三维模型。

陈鹰.2003.遥感影像的数字摄影测量［M］.上海:同济大学出版社.

官云兰，张红军，刘向美.2007.点特征提取算法探讨［J］.东华理工学院学报，30(1):42－46.

贾永红.2003.数字图像处理［M］.武汉:武汉大学出版社.

张祖勋，张剑清.1997.数字摄影测量学［M］.武汉:武汉大学出版社.

郑碧娜，江泽涛，吴敏.2009.一种基于立体像对稠密匹配的三维重建方法［J］.中国体视学与图像分析，14(2):187－191.

Moravec H P.1977.Towards automatic visual obstacle avoidance［C］.In Proceedings of the 5th International Joint Conference on Artificial Intelligence，Cambridge，Massachusetts，USA，584.

Lhuillier M，Quan L.2005.A quasi－dense approach to surface reconstruction from uncalibrated images［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，27(3):418－433.

Lowe D G.2005.Distinctive Image Features from Scale－Invariant Points［J］.International Journal of Computer Vision，60(2):91－110.

Ottog P，Chaut K W.1989.A“region－growing”algorithm for matching of terrain images［J］.Image and Vision Computing，7(2):83－94.

An Algorithm for Image Match Propagation

HE Liang， LIU Rong， LÜ Kai－yun
(Faculty of Geomatics，East China Institute of Technology，Fuzhou，JX 344000，China)

Stereo matching，an important part of 3D reconstruction，is widely used in digital cities，virtual reality.An improved match propagation algorithm is proposed.Firstly，the feature points are extracted and matched by SIFT algorithm.Then，the seed points are matched propagation in the neighborhood.Secondly，these dense correspondences are resampled to quasi－dense correspondences.Finally，the mismatched points and outliers are eliminated with epipolar constraint.Results show that this algorithm can be utilized for images with similar structure and without correction，and presents good performance.

SIFT algorithm;propagation;epipolar correction;quasi－dense matching

P232

A

1674－3504(2011)04－0379－05

贺亮，刘荣，吕开云.2011.一种基于种子生长的匹配算法［J］.东华理工大学学报:自然科学版，34(4):379－383.He Liang，Liu Rong，Lü Kai－yun.2011.An algorithm for image match propagation［J］.Journal of East China Institute of Technology(Natural Science)，34(4):379－383.

10.3969/j.issn.1674－3504.2011.04.012

2011－09－06; 责任编辑:吴志猛

江西省自然科学基金(2009GQS0001)

贺 亮(1986—)，男，硕士研究生，摄影测量与遥感专业。Email:hl_chn@163.com