航天器再入全过程轴对称烧蚀热防护数值仿真研究

张 涛，孙 冰(北京航空航天大学宇航学院，北京100191)

0 Introduction

When the reentry spacecraft returns to atmosphere in hypersonic speed，the atmosphere is strongly compressed and rubbed.Most part of kinetic energy is transformed to heat energy，it makes the temperature of the atmosphere that surrounds the spacecraft increase largely.The stagnation point temperature can exceed 8000K，the heat flux can exceed 10MW/m2and the highest pressure can reach 10Mpa［1－2］.In so bad circumstance，it is necessary that special thermal protection measures are taken to protect the spacecraft from destruction.So aerodynamic heat and thermal protection research is the fatal key technology of reentry spacecraft especially ballistic missile warhead.Ablation thermal protection is the most successful and the best method that is acknowledged now.Ablation thermal protection simulation mostly includes reentry heat environment，ablation rate，inner thermal response calculation and dealing with moving boundary［3－6］.Previous studies have concentrated on heating rates alone and ablation thermal protection simulation is realized with finite volume method and finite difference method［7－12］.The one dimensional ablation model is used mainly，it will bring error when the boundary conditions and internal thermal response don’t meet the one dimensional model conditions.At the same time，the previous studies mainly researched ablation theory，the numerical simulation key technology has not been researched deeply.This paper analyses and calculates axis symmetrical temperature field of reentry spacecraft，researches thermal response and ablation program for predicting charring material and carbon-carbon material and shape change on spacecraft in whole reentry.It can forecast thermal protection effect and provide theory basis for thermal design.

1 Constitution and functions of simulation system

The axis-symmetrical implicit thermal response and ablation program for predicting carbon-carbon and carbon based material and shape change on spacecraft in whole reentry based on Microsoft VC++6.0 is developed.The simulation program uses modularization design.The main function modules of simulation system are shown in Fig.1.Their functions and characteristics are shown as the following.

(1)Reentry trajectory calculation module:This module can provide the trajectory parameters of target for surface heat flux module.This module existing in-

Fig.1 Constitution of simulation system dependently can improve the applicability of simulation program.

(2)High temperature atmosphere thermodynamics and aerodynamic parameters module:This module calculates the surface pressure of target and properties of high temperature atmosphere.These parameters are the basis of surface heat flux calculation.

(3)Surface heat flux module:This module calculates the heat flux of target surface including convection，radiation and chemical reaction heat effect.The calculation results are the boundary conditions of temperature field calculation and basis parameters of thermochemical ablation.

(4)Thermochemical ablation rate module:This module uses JANAF model to calculate ablation rate and chemical ablation heat of carbon-carbon material and carbon based material.This module provides recession for grid generation module.

(5)Grid generation module and moving boundary and shape change process module:According to the ablation rate and boundary moving principle，the two modules can generate triangle elements for thermal response calculation.

(6)Internal thermal response calculation module:This module uses charred layer-pyrolysis surfaceoriginal material layer model.The temperature field is calculated with finite element method.This module provides temperature of ablation wall for thermochemical ablation calculation module.

2 Reentry heat flux calculation

The reentry heat flux on stagnation point is calculated with correctional Lees method and heat flux in other parts is calculated with reference enthalpy method［1－2］.The stagnation point heat flux is given by

Where q is heat flux;Pr is Prandtl number;ρ，μ and h are respectively the density，viscosity coefficient and enthalpy of atmosphere;The subscript s denotes stagnation point values and the subscript w denotes values of wall;The subscript e denotes values of boundary layer external margin;The superscript* denotes val-gradient of stagnation point.

Heat flux in laminar flow region is given by

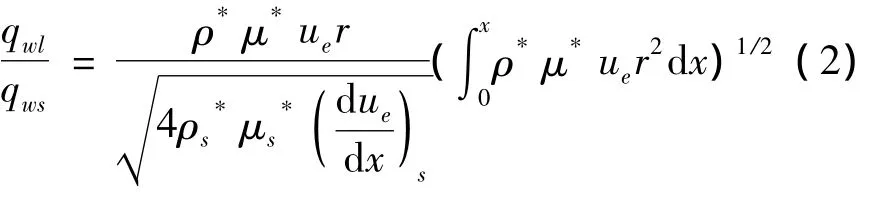
Where the subscript l denotes laminar flow value;r is radius of rolling body;x is the coordinate along surface from stagnation point.

Based on Blasius plane surface friction formula and Reynolds analogy theory，heat flux in turbulent flow region is calculated by resolved axis symmetrical momentum integral equations.The turbulent heat flux is

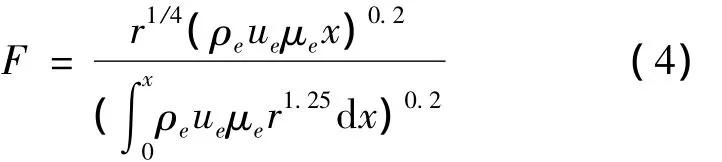
3 Ablation rate calculation

Ablation course in trajectory consists of oxidation diffusion control and sublimation diffusion control according to characteristic of reentry heat and thermochemistry of carbon.In simulation program，the following assumptions are introduced:all chemical reactions are on boundary surface and in chemical balance;over-all heat transfer coefficient is equal to mass transfer coefficient.

When wall temperature is larger than 1000K，CO is the only oxidation resultant of carbon.Surface oxidation reaction is［1－2］

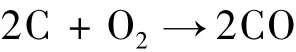
Gas on surface includes CO，O2，N2and pyrolysis gas.According to components conservation of mass，the component concentrations are

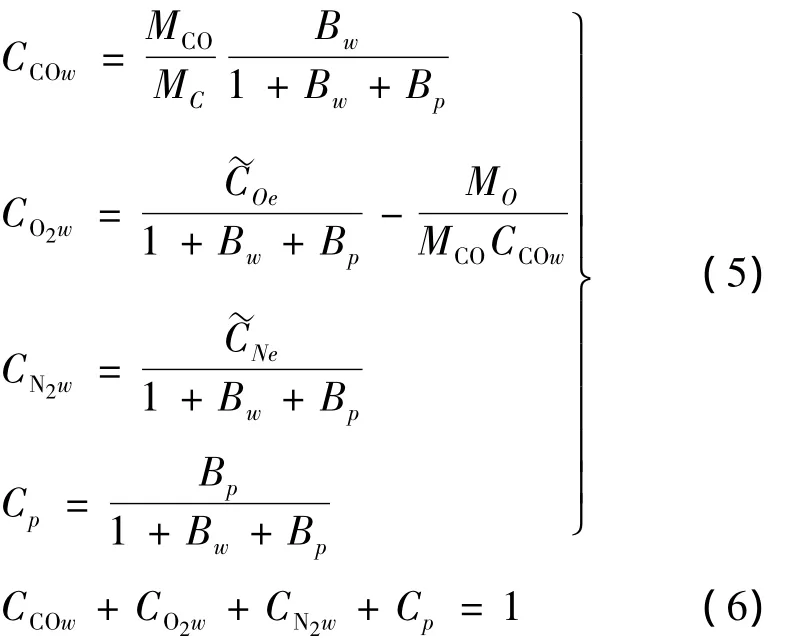
Where C denotes mass concentration;MOis oxygen atomic weight;MCis carbon atomic weight;~COeand~CNeare oxygen and nitrogen mass concentration of externalis mass loss rate of chemical ablation;˙mpis mass flux of pyrolysis gas;q0is cold wall heat flux without mass injection;hre is recovery enthalpy of boundary layer atmosphere;ψ is injection factor.

In the temperature range of oxidation diffusion control，oxygen gas is consumed completely.The oxygen gas concentration on wall surface is 0，where one parameter can be obtained［1］

Surface mass ablation rate is

When the flow state is laminar flow

When the flow state is turbulent flow

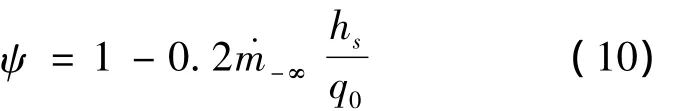
Where˙m－∞is the total mass flux of gas that flows into boundary layer.

When wall temperature is higher than 3300K，carbon sublimations appear.Carbon sublimation can produce single carbon，dual carbons，ternary carbons and so on.Experiment results show that calculation results of JANAF model are the most coincident with experiment results.In this paper JANAF model is used.When the wall temperature is higher than carbon sublimation temperature，carbon and nitrogen will react.The gas components on wall surface include O2，O，N2，N，CO，CN，C2N，C1，C2，C3，C4，C5and pyrolysis gas.

4 Thermal response calculation

4. 1 Physics model analysis

The reentry spacecraft includes nose tip and conic body.Ablation material is carbon-carbon material in nose tip and carbon based composite material in conic body as shown in Fig.5.

When spacecraft returns into aerosphere without attack angle or attack angle is very small，the thermal response of ablation materials can be analyzed as axis symmetrical model.Because the factors of effecting temperature field are very complex，this paper is under the following assumptions［13－15］:

(1)Charred layer-pyrolysis surface-original material model layer is applied to carbon based composite thermal response model.

(2)Pyrogenation reaction only appears on pyrolysis surface and pyrolysis surface keeps constant temperature.

(3)When pyrolysis gas flows through charred layer，the pyrolysis gas and charred layer have no temperature difference.

(4)Surface chemical reaction heat all enters charred layer.

This paper uses the same ablation calculation model for carbon-carbon and carbon based composite materials.The carbon-carbon materials only have charred layer and have no pyrolysis surface and original material.

4. 2 Mathematical models

As shown in Fig.2 ，the conduction equation of charred layer is［16－19］

The conduction equation of original material layer is

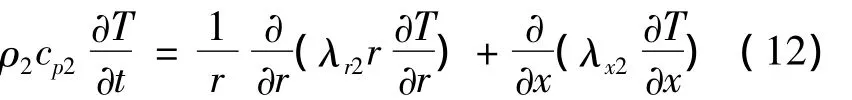
The boundary condition on charred layer outer boundaryГ4is

Pyrolysis surface boundary condition onГ5is

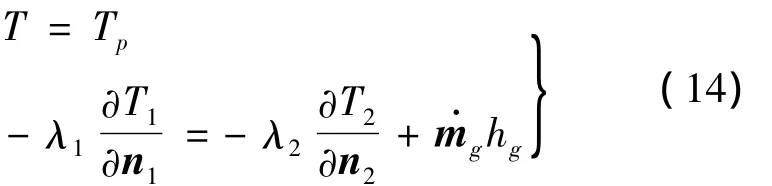
Where n is unit vector of outer normal direction of Г4;n1and n2are unit vector of normal ofГ5.n1directs original material layer and n2directs charred layer.

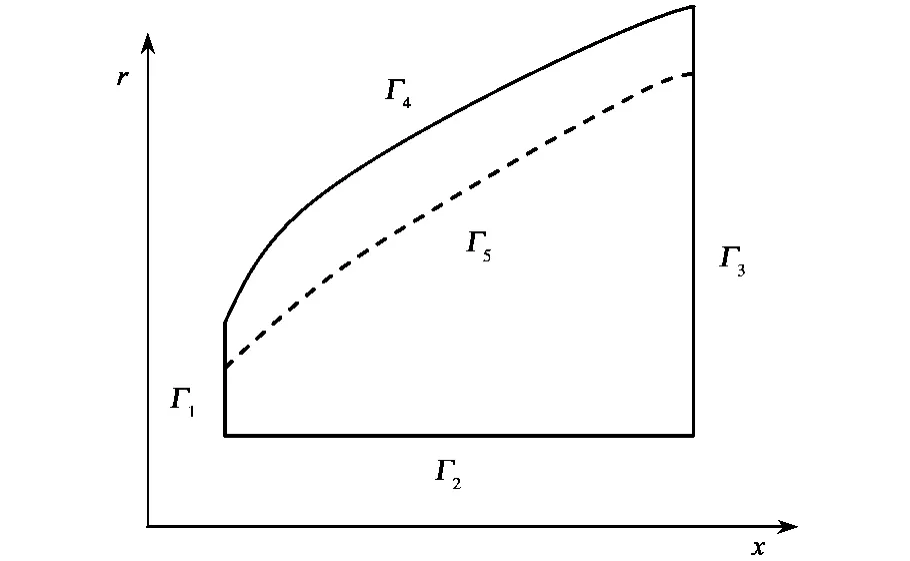
Fig.2 Sketch map of three layers model

Where ρ，cp，λ，h are density，specific heat，heat conduction coefficient and pyrolysis potential heat;˙mgis mass flux of pyrolysis gas.Subscript 1 denotes parameters of charred layer;subscript 2 denotes parameters of original material;subscript g denotes parameters of pyrolysis gas.

Heat flux qNfrom ablation boundaryГ4to charred layer is［1］

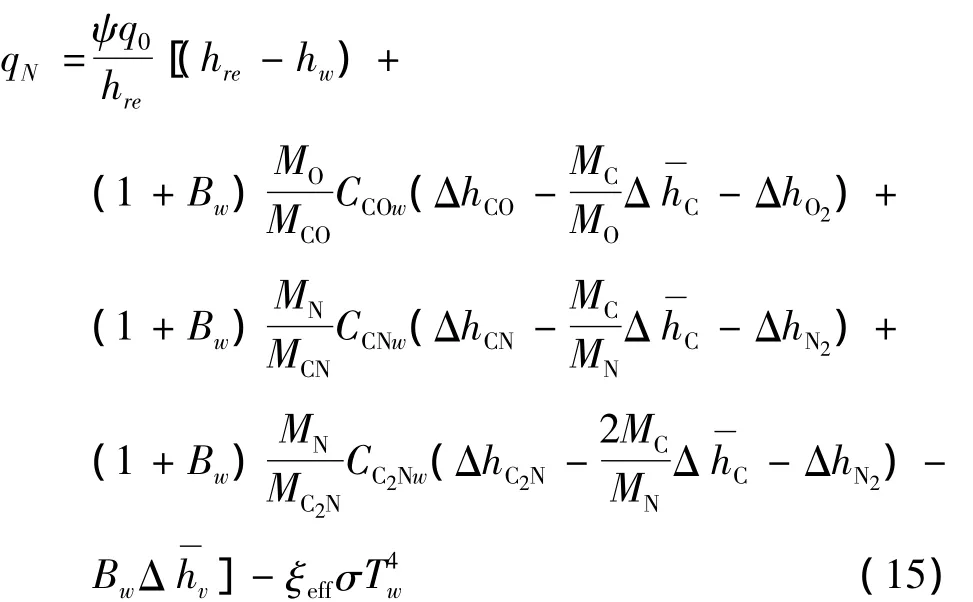
WhereΔhCOis gaseous combustion heat of carbon;ΔhCNandΔhC2Nare reaction heat of carbon and nitro-is average sublimation heat of carbon;ΔhO2is decomposing heat of oxygen molecule;ΔhN2is decomposing heat of nitrogen molecule.

The sublimation fraction is

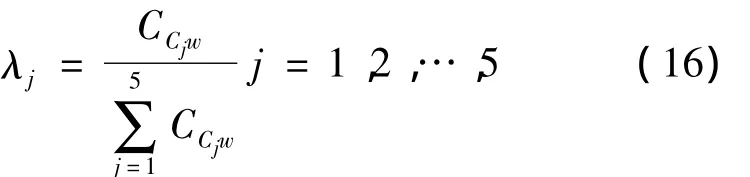
Where two parameters can be obtained from Eq.(16)

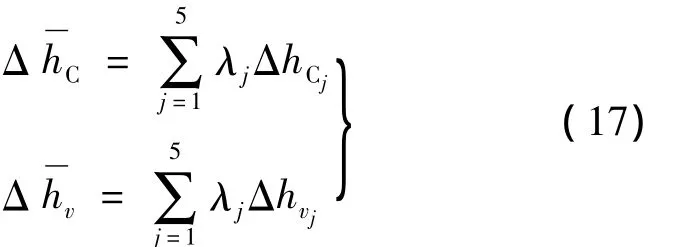
WhereΔhCjis decomposing heat of carbon;Δhvjis average sublimation heat of carbon。

4. 3 Dealing with unsteady term

This paper uses triangle grid.The grid is generated with transfinite interpolation method.Method of dealing with moving boundary and finite element processing for Eq.(11)and Eq.(12)have been researched in reference［20］ by author of this paper.This paper applies the same method.

Because heat flux of surface of reentry spacecraft is very big，the unsteady temperature field calculation needs special process，or it will result in numerical oscillation and temperature result disobey heat transfer law.The following equation can be obtained through finite element method

Where H is the conductance matrix，C is the capacitance matrix and p is the heat load vector.

This paper uses the following format to deal with

Where the subscript t denotes calculation time step，t－ Δt denotes the last time step，Δt denotes step length.

Because H and p contain unknown temperature T，Eq.(19)needs to be solved with iterative method.In every time step，Eq.(19)may be rewritten as:

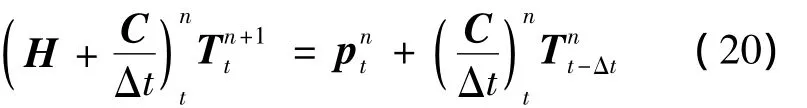
Where the superscript n denotes the n times iteration in t time step.

For big heat flux on boundary of reentry spacecraft，this paper uses the following relaxation factor to reduce numerical oscillation.

relaxation factor 0＜β＜2。

The grid element side lengthΔx and time step lengthΔt need to satisfy the following condition

Where a is thermal diffusivity.Generally，it can increase the stability and precision of numerical calculation by decreasing time step lengthΔt.But when element side length Δx is a certain value，Δt needs to meet the Eq.(22).IfΔt is smaller than the limit which is calculated through Eq.(22)，the numerical oscillation will appear［21］.

The temporal and spatial numerical oscillation of unsteady temperature field calculation comes from discretizing the governing equation which changes problems from infinite degrees of freedom to finite degrees of freedom.For the stiffness of discretized equation，the response speed for heat load is finite.The reentry heat flux is very big，the low response speed of discretized equation will cause heat accumulation or rapid-ly decrease on some nodes to result in numerical oscillation.

Through research，it is found that numerical oscillation can be restrained effectively when the heat capacity matrix is lumped by using backward difference scheme and the computational efficiency will not be decreased.

The conductance matrix H is product of mass matrix of element and specific heat.The matrix is n ranks banded symmetric matrix.Because the thermal conductivity of ablation material is very small，the internal thermal response has shock effect with the big heat flux boundary condition.For numerical calculation convergence，it needs very small calculation grids.For increasing calculation efficiency，when the boundary heat flux is very big and the thermal conductivity is relatively small，it can be considered that the heat flux into some nodes is only related to the nodes’temperature change.

This numerical oscillation problem can be solved well by converging the mass of element to nodes.This paper adds all elements of every row to diagonal elements.The capacitance matrix can be rewritten as

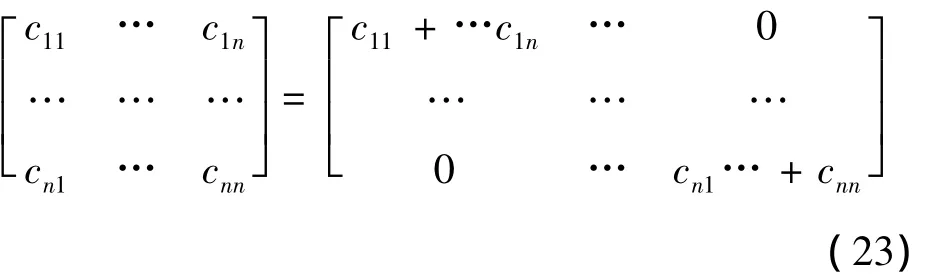
Therefore，all matrix elements are zero except diagonal elements.

From Eq.(23)，it is rational that the heat flux into some nodes is only related to the temperature change.

4. 4 Mass flux of pyrolysis gas calculation

In the simulation program，it needs to judge the position of charred layer，pyrolysis surface and original material layer at first.Because the simulation region has been discretized to triangle grid，the geometry information is substituted by triangle elements and nodes.If one node temperature of some element is higher than pyrolysis temperature TP，the element is treated as charred layer element.The material properties of this element are charred layer material properties.

In theory，the pyrolysis surface is the common boundary of charred layer and original material.The pyrolysis surface boundary can be rewritten as

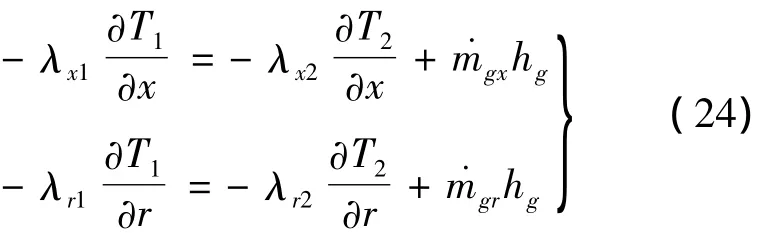
When grid is discretized，the position of pyrolysis surface can’t be fixed.After grid is discretized，the pyrolysis surface may be inside elements as shown in Fig.3.To calculate pyrolysis gas mass flux，it needsement E1has only one node whose temperature is higher than TPor equal to TP，the rest two node temperatures are lower than TP，and element E1has only one adjoining element E2of original material.According to this condition，the pyrolysis surface is inside element E1.As shown in Fig.4，if element E1has no adjoining element，it denotes that E1is on insulation boundary.This paper uses linear function as temperature field in-in every triangle element.So as shown in Fig.3，pyrolysis gas mass flux is

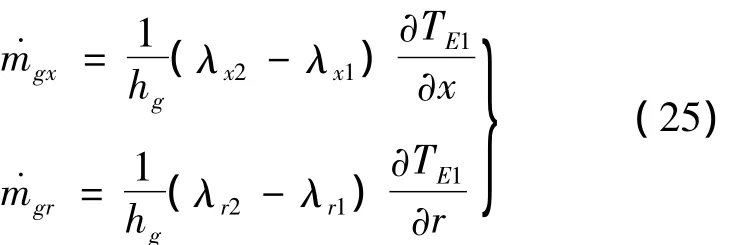
Fig.3 Sketch map of axis symmetrical pyrolysis surface

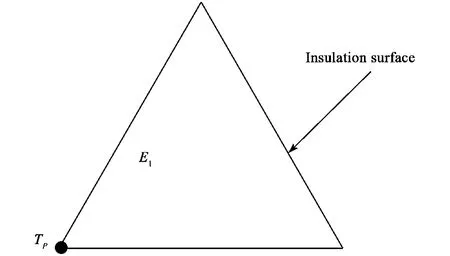
Fig.4 Boundary element of axis symmetrical Insulation surface

5 Simulation result and analysis

The axis symmetrical temperature field calculation program with finite element method has been tested and validated in reference［20］.This paper mainly analyzes and calculates ablation rate，pyrolysis gas mass flux and temperature field.The structure of calculation sample is shown as Fig.5.The reentry trajectory is a typical non-thrust one.The reentry velocity is 6000m/s，reentry angle is －20°，reentry altitude is 30km.The reentry body is nose tip radius of 0.2m，the cone half angle of 12°，whole length of 1.5m，weight of 1000kg.The initial temperature is 350K.

The reentry height and velocity of spacecraft are given in Fig.6 and Fig.7.

Fig.5 Sketch map of axis symmetrical configuration

The shape changes are given in Fig.8 and Fig.9.Because turbulent flow heats up，the heat flux in the point where the flow velocity is velocity of sound is much higher than the stagnation point.As shown in Fig.8，the maximal shape change point is not in stagnation.As shown in Fig.9，the recession in the conic body is higher than in the nose tip.This is because that the anti-ablation capability of carbon-carbon material is stronger than the carbon based material.

Fig.6 The trajectory height of reentry spacecraft

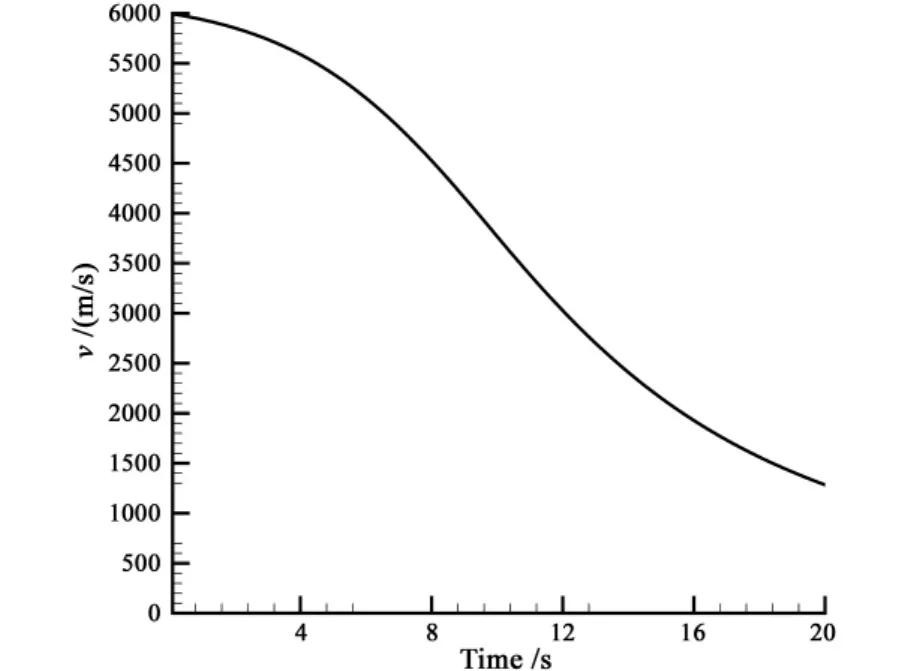
Fig.7 The velocity of reentry spacecraft

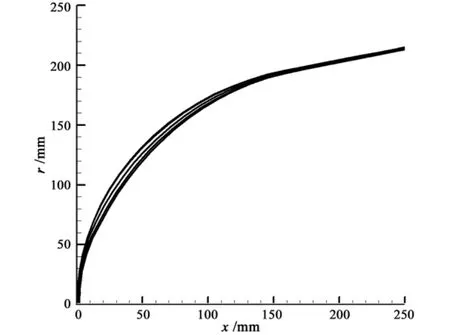
Fig.8 The nose tip shape change of reentry spacecraft

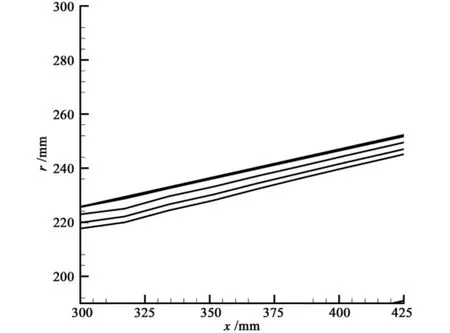
Fig.9 The shape change of conic body

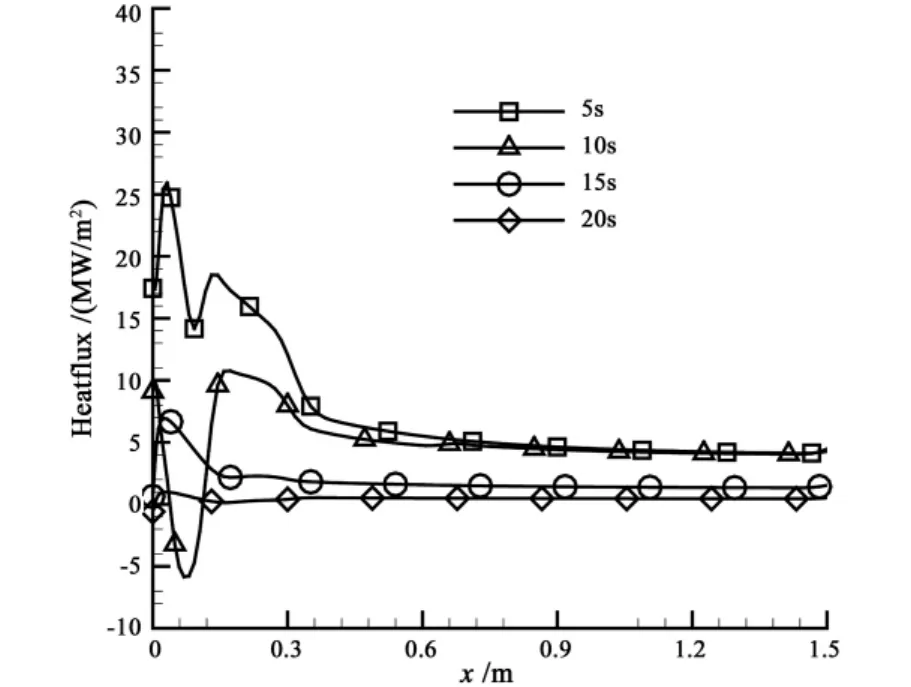
Fig.10 The total heat flux qN entering reentry spacecraft

Fig.11 The recession distributions of reentry spacecraft

The surface heat flux and recession distributions are given in Fig.10 and Fig.11.As shown in Fig.10，the heat flux entering the surface of spacecraft increases at first，then it declines.At the beginning，the wall temperature is low and the atmosphere temperature is high，the high temperature atmosphere heats the wall of spacecraft.When the spacecraft velocity declines，the thermal energy and temperature of surface atmosphere will decline.But the spacecraft wall temperature increases all the time.When the wall temperature is higher than the atmosphere temperature，the wall will heat the atmosphere and the wall temperature will decline.When the heat flux is negative，it means that the temperature of surface begins to heat the atmos-phere.Because the wall temperature increases at beginning and declines then，So the recession increases at first，then it declines.As shown in Fig.11，the stagnation point heat flux is not the greatest position，so the greatest recession appears in the position that has a distance from stagnation point.In Fig.12，the pyrolysis gas mass flux increases quickly and then it is almost a constant.This is because that the pyrolysis gas mass flux is affected by the increasing rate of temperature.At the beginning of reentry，the temperature increases quickly，so the pyrolysis gas mass flux increases quickly.

Fig.12 The pyrolysis gas mass flux

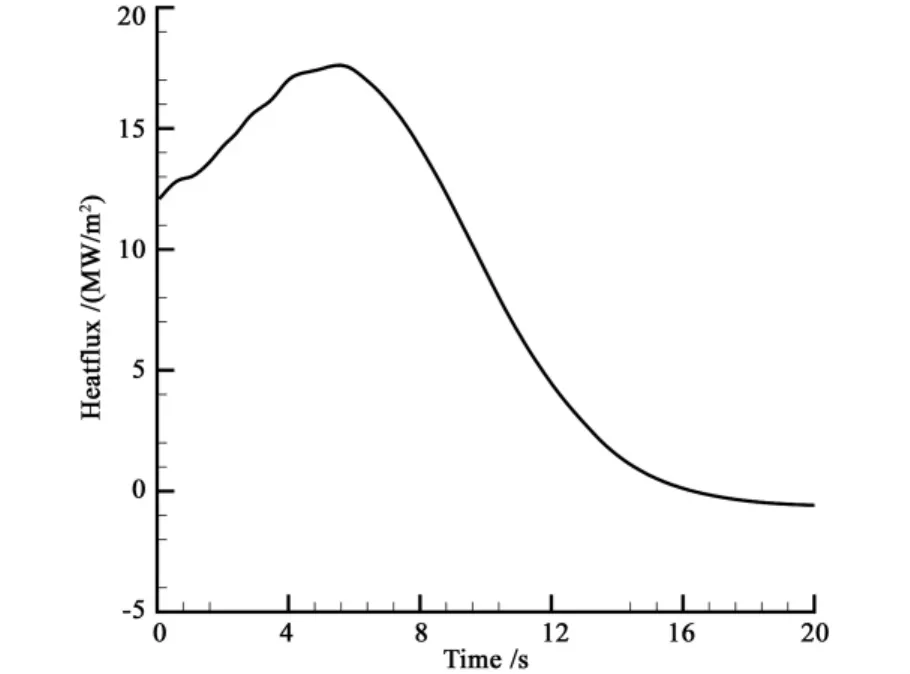
Fig.13 The stagnation point heat flux

Fig.14 The stagnation point temperature

Fig.15 The stagnation point recession

The heat flux，temperature and recession of stagnation point are given in Fig.13，Fig.14 and Fig.15.Because the stagnation point material has high density，specific heat and heat conductivity，the temperature and recession of stagnation point is not very high.It shows that the carbon-carbon material has better antiablation characteristic than carbon based material.The results also have the same variation trend with the results of reference［3］.It can prove that the simulation program is reliable.

6 Conclusions

The axis-symmetrical implicit thermal response and ablation program for predicting carbon-carbon and carbon based material and shape change on spacecraft in whole reentry is developed.The key technology of numerical calculation is researched.The main problems， for example， numerical oscillation， moving boundary，are solved well.From the calculation sample，it has been demonstrated that the simulation model is rational，the calculation methods are accurate and each calculation module can realize corresponding calculation function.The simulation program is not only useful for calculation of thermochemical ablation，reentry surface heat flux，thermal response calculation and reentry trajectory，but also can be extended to analyze and calculate the stress field of thermal protection system.At the same time，three dimensional thermal response and ablation program for predicting carbon-carbon and carbon based material and shape change in whole reentry is being developed.

［1］ Zhang Z C.Supersonic aerodynamic heating and thermal protection［M］.BeiJing:National Defence Industry Press，2003.

［2］ Wang G X，Zeng QX，An F X.Warhead technology［M］.Bei-Jing:Astronautics Press，1991.

［3］ Chen Y K，Milos FS.Two-dimensional implicit thermal response and ablation program for charring materials［J］.Journal of Spacecraft and Rockets，2001，38(4):473 －481.

［4］ Chen Y K，Milos F S.Ablation and thermal analysis program for spacecraft heat shield analysis［J］.Journal of Spacecraft and Rockets，1999，36(3):475 －483.

［5］ Jia F，Galea E R.Numerical simulation of the mass loss process in pyrolizing char materials［J］.Fire and Materials，1999，(23):71－78.

［6］ Hogge M，Gerrekens P.Two-dimensional deforming finite element methods for surface ablation［R］.AIAA 83－1555.

［7］ Blackwell B F.Numerical prediction of 1－D ablation using a finite control volume procedure with exponential differencing［R］.AIAA 88－0085.

［8］ Blackwell B F，Hogan RE.Numerical solution of axis symmetric heat condution problems using finite control volume technique［J］.Journal of the Mophysics and Heat Transfer，1993，7(3):462－471.

［9］ Blackwell B F，Hogan R E.One-dimensional ablation using laundau transformation and finite control volume procedure［J］.Journal of Themophysics and Heat Transfer，1993，6(2):282 －287.

［10］ Amar A J.One-dimensional ablation with pyrolysis gas flow using a full Newton’s method and finite control volume procedure［R］.AIAA 2007－4535.

［11］ Subrahmanya S，Katte SK，Das SP，et al.Two-dimensional ab-lation in cylindrical geometry［J］.Journal of Thermophysics and Heat Transfer，2000，14(4):548 －556.

［12］ Hogan R E，Blackwell B F，Cochran R J.Numerical solution of two-dimensional ablation problems using the finite control volume method with unstructured grids［R］.AIAA 94 －2085.

［13］ Ahamad Reza Bahramian.Ablation and thermal degradation behaviour of a composite based on resole type phenolic resin:Process modeling and experimental［J］.olymer 47(2006)3661 －3673.

［14］ Jaworske D A，Gaier J R，Podojil G M，et al.Durability of carbon-carbon composites to a simulated martian atmosphere［R］.AIAA 94－2629.

［15］ Hugh L N，McManus，Gerorge S，et al.High temperature thermomechanical behavior of carbonphenolic and carbon-carbon composites［J］.Journal of Composite Materials，2006，26(2):206－229.

［16］ Murray A L，Russell G W.Coupled aero heating/ablation analysis for missile configurations［J］.Journal of Spacecraft and Rockets，2002，39(4):468 －475.

［17］ Hugh L N，McManus，George S.Springer.High temperature thermomechanical behavior of carbon-phenolic and carbon-carbon compositesⅠ analysis［J］.Journal of Composite Materials，1997，26(2):206－229.

［18］ Dimitrienko YU I.A structural themomechanical model of textile composite materials at high temperature［J］.Composites Science and Technology，1999，59(7):1041 －1053.

［19］ Dimitrienko YU I.Internal heat mass transfer and stress in thinwalled structures of ablating materials［J］.Int.J.Heat Mass Transfer，1997，40(7):1701 －1711.

［20］ Zhang T，Sun B.Numerical computation of solid rocket motor insulation layer temperature by finite element method［J］.Journal of Aerospace power，2009，24(6):1407 －1412.

［21］ Kong X Q.Finite element method application in heat transfer［M］.BeiJing:Science Press，1998.