数理统计法结合仿真曲线优化纸浆浓度仪标定

廖一致 罗超 岳阳纸业股份有限公司自控分公司 湖南 岳阳 （414002）

数理统计法结合仿真曲线优化纸浆浓度仪标定

廖一致 罗超 岳阳纸业股份有限公司自控分公司 湖南 岳阳 （414002）

纸浆浓度仪在制浆造纸工厂广泛应用于纸浆浓度计量与控制，浓度仪表出厂的主要性能指标是灵敏度与重复性。而实际应用的精度保证通常需要在工厂进行标定，标定效果决定了使用效果。尤其是应用于浆料配比控制与产量计量的情况，传统的标定方法没有办法保证作为计量应用的仪表精度。针对高精度应用要求的场合，采用数理统计的方法进行数据的预处理与再筛选，减少因人工采样化验造成的误差，并且通过参比曲线进行逐步减小误差的方法，最终能够将标定优化达到实际应用要求的精度。

浓度计量；标定；优化。

近几年公司为了加强成本管理与考核，将原来浆系统输送到造纸车间的浆料浓度控制提高到产量计量要求，为了满足浆量计量更高精度的需要，我们在选型时采用了当今市场上灵敏度与重复性比较好的内旋式浓度计，而且为了达到计量精度更高的要求，我们开展了以下的有超越于传统方法的标定优化工作来满足新的精度要求。

1 浓度仪的基本构成与工作特性

如图1所示内旋式浓度计的结构图。它的工作原理是：连接螺旋桨的驱动轴由电机直接驱动，而连接传感器的测量轴通过弹性联接跟随驱动轴旋转，并且测量轴与驱动轴分别配置有凹槽轮。由于浆纤维剪切力的存在，使得测量轴与驱动轴在转动过程中产生相对偏转，也就是说浆纤维的阻力矩使得测量轴的转角落后于驱动轴。这种转角差通过凹槽轮与光学装置可以测量得到，并通过采集放大电路转换为相应的电信号。控制电路则根据转角差信号调整反馈电流，并由此产生平衡转矩用于平衡浆料纤维的剪切力矩，使两轴之间的转角差在反馈力的作用下维持在预先设定的一个恒定值。这时反馈电流的大小就反映了相应浆料纤维所产生的阻力转矩的大小，而阻力转矩的大小是和相应的浓度对应的。这种反馈电流就是仪表中的参数feedback，单位为百分数。这种反映浓度大小的feedback值经放大转换并规格化为4-20mA输出。仪表出厂试验得出，feedback值的大小与浓度（CONS）构成二次函数关系（Feedback=K0+K1 x cons.+K2 x cons2.），其中常系数 K0、K1、K2取决于不同的浆种与不同的工况条件。原理框图：

图1 内旋式浓度仪结构原理图

2 浓度仪的标定原理

仪表制造完成，它的工作特性就已经确定，但是浓度仪为了适应不同的浆种，通常需要我们在工厂应用时进行现场标定，也就是将仪表的特性关系式（Feedback=K0+K1 xcons.+K2 x cons2.）中的未知系数K0、K1、K2确定。理论上，我们需要给出3个feedback与浓度数据对，才可以将上式确定。

由图2可以看出，我们只要将化验数据与采样时对应的仪表参数feedback值输入浓度仪表，借助于仪表本身的计算功能就可以得到图示的关系曲线，然后设定浓度测量范围，即得到线性输出关系（浓度-mA）。

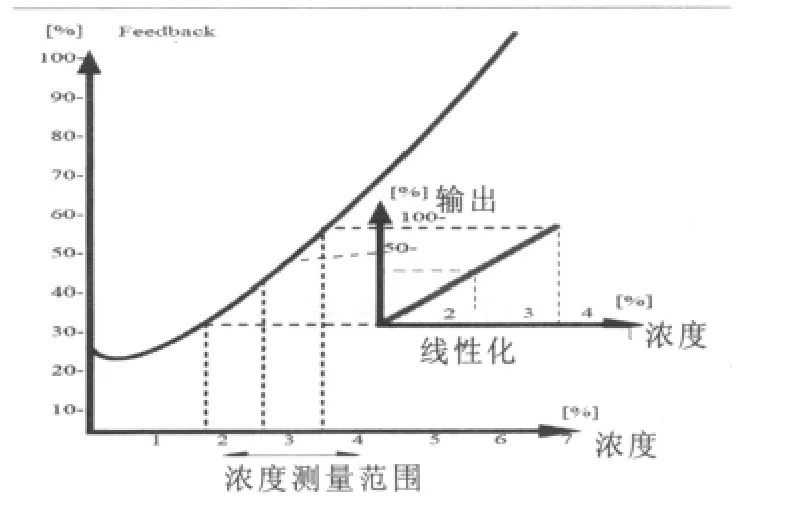
图2 原始数据与浓度函数关系及线性化图

3 原始数据处理

理论上由浓度标定原理知道，我们只需要给出3个feedback与浓度数据对（feedback、浓度cons），特性关系式Feedback=K0+K1 x cons.+K2 x cons2.）就可以确定。但是，实际上我们不可能采集到理论上准确的化验数据，因此我们得出的关系函数也就不是精确的或者说不是正确的工作函数关系，也就可能造成较大的仪表工作误差。为此仪表本身的数据处理程序就考虑了采样数据的非真实性而可能造成较大的测量误差，因而内部进行了离散数据的回归分析，自动计算出关系曲线，并推荐输入较多的（远远多于3个）数据以确保减小非真实采样数据对结果的影响。对于一般的过程控制应用场合，通常采用这样简单处理的方法就可以满足生产控制要求。但是，对于高要求的配比控制与产量考核计量，这样的办法就远远达不到我们的高精度要求。

为了建立精确的关系曲线，确保标定的准确性，我们在浆量计量的实际应用中通常需要对原始数据进行筛选处理。具体做法是：适当增加采样数据，并利用取样化验平均值、线性与非线性筛选的办法去除偏离真实值较大的数据。

取样化验平均值：某一浓度点，同时采集2-3个样本进行化验，将化验结果进行平均计算，筛出偏离平均值较大的化验值，减少化验操作误差的影响。

线性筛选：基于小范围数据可以近似为线性关系，采用数学方法将离散数据进行线性回归分析，将偏离曲线较大的数据筛除。也可以利用office软件的excel工具生成一次函数曲线，将偏离曲线较大的数据筛除。非线性筛选：采用数理统计的方法将离散数据进行多项式回归分析，得出回归方程，将偏离曲线较大的非真实数据筛除。最方便易行的方法是利用office软件的excel工具生成对应的二次函数与趋势曲线，然后利用excel工具逐点自动计算出各点的残差，将残差较大的点从样本中删除，这样得出的样本数据的相关性就更好。然后再以筛选的样本建立回归方程与回归曲线，这样的关系曲线就更接近于理想曲线。

通过这样的筛选，可以大大提高一次标定效率，较快地接近目标效果。

下面对表1的数据进行相关的处理。

表1 采样浓度数据

首先借助于Excel散点图的趋势线功能对以上数据（feedback，实际检测值）进行回归分析，得出回归方程与回归曲线如下。

回归方程：feedback=2.185cons2-3.86cons+17.09

图3 原始数据回归生成的特性曲线

在以上回归方程的基础上，我们可以方便地计算残差，然后将残差范围控制在-2＜δ＜2（针对本例）,筛选出序号8-19为有效数据，并应用这些数据进行再次回归分析得出新的回归方程与回归曲线。

新的回归方程为：

feedback=2.2225cons2-3.758cons+16.07

图4 原始数据筛选处理后生成的特性曲线

显然筛选出的数据相关性更好。这样，我们可以选择几个典型的浓度点通过回归方程进行计算相应的feedback 值，建立 3 个(feedback，cons)数据对，将这样几组数据经过手操器计算并传送到浓度计的内存，就可以将曲线在浓度计中再现，相当于将这样的标定曲线传送到了浓度仪，这样就完成了一次标定。例如计算出数据对为：（20.57，2.5%）、（36.6，4%）、（62.6，5.5%）。

4 标定参数优化（误差逼近）

尽管我们通过以上的数据筛选措施，得到相对接近于理想的函数关系（标定曲线），但是由于采样与化验操作造成的数据误差，仍然可能使得我们的标定曲线偏离理想曲线。为了确保仪表工作精度，还需要在此基础上进行标定参数优化。通常没有参比的优化是比较困难的。于是仿真曲线给我们提供了很好的帮助。具体做法是，我们将新的采样数据进行处理，得出误差分布情况，利用在用的回归曲线做为参比曲线，使我们非常清楚直观地了解到标定曲线需要调整的方向。

例如，一次标定后，我们采集了如下数据。并得出误差分布图。

表2 基本标定后采样浓度数据

根据表2的测量值、化验值以及相应的误差可以做出分布图5如下：（当然通常我们需要采集更多的点，同样可以减少化验误差的影响）。

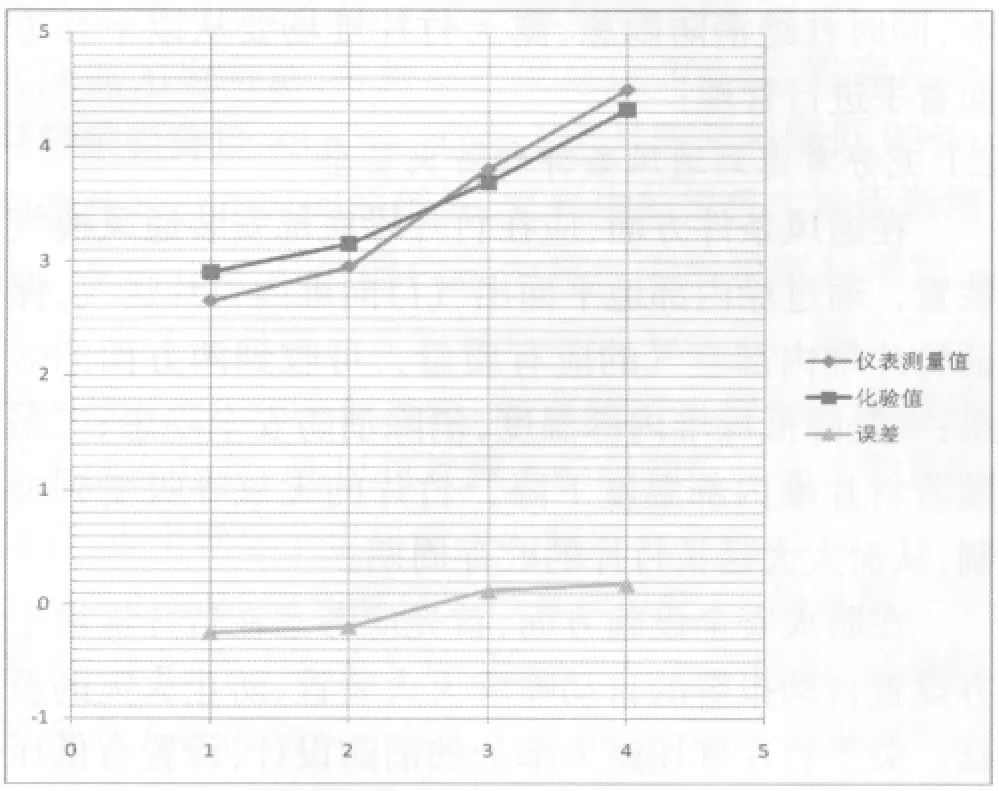
图5 一次标定后采样的数据分布图

根据误差分布，我们就可以做减小误差的曲线调整。见表2，表中“调整浓度值”就是相应feedback值下进行误差校正的新浓度值。需要注意的是，我们不要期望将误差一次消除，而是遵循大部分消除（将误差消除60%）与逐步逼近的原则。于是，建立了新的调整方程feedback=2.818cons2-5.78cons+15.95与调整曲线。

图6 运行曲线与调整曲线比较图

同样，我们可以根据调整方程feedback=2.818cons2-5.78cons+15.95计算出如表3中的标定数据。

表3 ：由调整方程计算出的标定数据

将表3的数据输入浓度仪就完成新一次的标定。显然，这样的标定需要进行几个周期，然后可以将误差逐步减小，最终达到实际应用的精度要求。

总结

优化浓度标定的方法不但适用于一般应用场合，尤其适用于配比控制、产量计量等高精度要求的应用场合，可以将工作曲线直观地逼近理想特性曲线，使仪表工作误差逐步减小，最终将精度标定到实际需要，避免了传统标定方法对精度调整的盲目性，具有实际应用推广价值。

[1]BTG浓度计使用与维护手册

[2]盛骤等.概率论与数理统计.高等教育出版社.1989.8

[3]金治明等.概率论与数理统计.国防科技大学出版社.1998.3

2010-4-6