同步电机瞬态和超瞬态电抗的有限元计算

王 斌

(上海电机厂有限公司，上海200240)

0 引言

同步电机的瞬态和超瞬态电抗对电机的瞬态运行性能(包括瞬态稳定性、三相和其他不对称突然短路过程以及非同期合闸过程等)有着重要的影响。因此，精确计算同步电机的瞬态和超瞬态电抗对同步电机的设计及电机瞬态过程的分析和仿真都有重要意义。

瞬态和超瞬态电抗磁路法计算公式虽然在传统的电励磁同步电机中得到了较好的应用，但却无法适用于新型结构的同步电机(以实心磁极代替阻尼条的凸极同步电机、永磁同步电机等)。随着计算机技术和有限元分析软件的飞速发展，如何从磁场的角度出发，用数值方法较准确地计算出同步电机的瞬态和超瞬态电抗，一直受到国内外学者的关注，并做了大量的工作［1-4］。

基于磁场分析的同步电机瞬态和超瞬态电抗的有限元计算方法的基本思想是根据电机电磁场理论，将超导体电路在瞬变之后具有永远保持其磁链不变的特性引入有限元分析模型，模拟同步电机瞬态和超瞬态的瞬变时刻的工况。

将据此推导该新方法的理论表述，并结合实例给出新方法与传统方法计算的瞬态和超瞬态电抗结果的对比。

1 瞬变时刻的运算电抗分析

同步电机在瞬态运行工况下，在瞬变时刻，各无源闭合电路(励磁绕组、阻尼绕组)为了保持其磁链不变，会在相应的绕组中感应出瞬变电流，而且这些瞬变电流还要按照一定的时间常数逐步衰减至其稳态值。如果这些电流不衰减，即其时间常数为无限大，则这些电流将保持其起始值而不变。

任何感性闭合电路在瞬变之初恒有保持其磁链不变的特性，而超导体电路则在瞬变之后具有永远保持其磁链不变的特性。因此，上述电流的起始值，可以利用超导体电路的概念来求解。

以同步电机突然三相短路为例，利用叠加原理，即认为不是发生了突然短路，而是在电机的端头上突然加上了与电机突然短路前的端电压大小相等但方向相反的三相电压;并假定无励磁电压的调节作用［5］。在短路瞬间，根据上面的分析，可以将转子绕组的电路(阻尼绕组和励磁绕组)考虑为超导体电路，即令转子电阻为零。根据同步电机的运算等值电路，如图1a、b所示。可以得到此时的直轴、交轴运算电抗为:

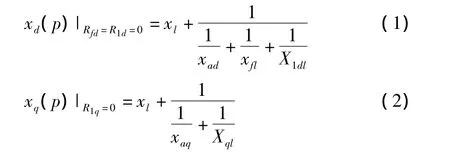
上式中的直轴、交轴运算电抗就分别称为同步电机的直轴、交轴超瞬变电抗(从超瞬变电流衰减时间常数的角度推导也可以得到相同的结果)。

同理，在转子绕组没有阻尼绕组时，可等效于存在阻尼绕组，但是阻尼绕组开路，励磁绕组仍为超导体电路，可以得到此时的直轴运算电抗为:

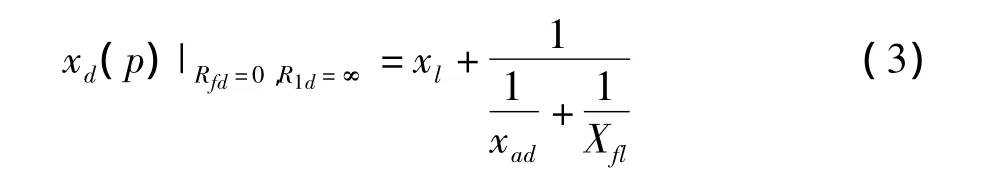
上式中的直轴运算电抗就称为同步电机的直轴瞬变电抗。

总结(1)、(2)和(3)式不难发现，这就是传统同步电机设计中瞬态、超瞬态电抗的计算公式。传统的瞬变、超瞬变电抗计算是以等效磁路为基础，计算出同步电机运算等值电路中的各个参数，最后根据上面推导的式子计算得到。传统的方法存在许多的局限性，比如磁路化的假设、饱和情况的近似考虑、对新结构电机无法适用等。

上述传统方法中存在的问题，通过有限元分析基本可以得到解决。而且通过上面的分析可以发现，只要能模拟转子绕组为超导体电路的运行情况，此时计算得到的定子绕组电抗即为同步电机的瞬变、超瞬变电抗，而有限元进行超导体电路建模模拟非常的简单方便。

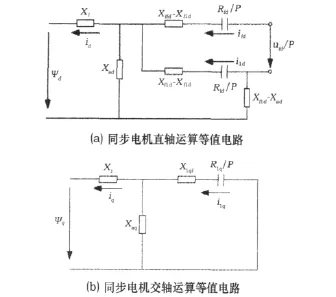
图1 同步电机运算等值电路

2 瞬变、超瞬变电抗有限元计算方法

2.1 原有的有限元计算方法

从场的角度出发，在使用有限元较准确的计算同步电机的瞬态和超瞬态电抗方面，国内外学者作了大量的工作，提出了一些计算方法。

梁艳萍、汤蕴璆等用有限元法结合频率特性来计算水轮发电机的瞬态电抗［6］。该方法由于结合频率特性，所以前提即要求绕组磁链为正弦，对于凸极电机、表面贴永磁电机，绕组磁链分布距离正弦波形有一定差距，即使取三相平均值，仍难避免此问题。

梁艳萍、周封等用时步有限元法计算汽轮发电机直轴瞬态参数［7］。该方法采用时步有限元瞬态计算，避免了频率特性计算正弦前提的问题，但是由于数据的后处理涉及到了电流曲线的包络线绘制、曲线的拟合等操作，因此相当繁琐，而且极容易产生偏差。

2.2 参数计算方法

根据第1节中的分析，笔者提出一种基于磁场分析的同步电机瞬态和超瞬态电抗的有限元计算方法。新方法采用瞬态电磁有限元，对同步电机直线部分的整个二维横截面进行建模、分析，通过输入端部漏电抗来模拟端部效应。

忽略绕组导体中交变磁场引起的涡流集肤效应。整个横截面模型用自适应网格剖分求解。通过有限元分析求出整个场域上各节点上的矢量磁位，并得到场域内磁场的分布。

2.2.1 超瞬变电抗

以A相绕组为例。首先，将励磁绕组短接，并将阻尼绕组、励磁绕组的材料均设为超导体(比如电导率设为1e17西门子/m)，永磁材料设为空气;其次，设置转子转速为0，将A相绕组的中心线对准直/交轴;然后，在电机定子绕组端加载三相对称正弦波电压，最后得到瞬时A相电流曲线。A相电压和电流(稳定值)的比值即为直/交轴超瞬变电抗Xd″/Xq″。

2.2.2 瞬变电抗

以A相绕组为例。首先，将励磁绕组短接，励磁绕组的材料设为超导体(比如电导率设为1e17西门子/m)，并将阻尼绕组、永磁材料设为空气;其次，设置转子转速为0，将A相绕组的中心线对准直轴;然后，在电机定子绕组端加载三相对称正弦波电压，最后得到瞬态A相电流曲线。A相电压和电流(稳定值)的比值即为直轴瞬变电抗Xd'。

3 瞬变、超瞬变电抗计算结果对比

以一台6 000 kW，6 600 V，4极隐极同步电机为例，采用笔者提出的新方法，计算直轴瞬变、超瞬变电抗，并将新方法的计算结果与传统磁路分析方法的结果对照，验证新方法的有效性。

3.1 直轴超瞬变电抗

按照2.2节提出的新方法，直轴超瞬变电抗的计算结果如下，各波形参见图2。

图2 直轴超瞬变电抗有限元分析结果

定子机端相电压有效值:3 810.6 V

定子稳态相电流有效值:7 355.5 A

直轴超瞬变电抗实际值:0.518 1 Ω

直轴超瞬变电抗标幺值:0.089 2

从图2(c)可以发现，在超瞬态瞬变时刻，由于阻尼绕组和励磁绕组维持其磁链不变，于是这两个绕组里要感应电流，产生各自的反磁链，去抵消电枢磁通;从磁力线图上来看，电枢磁通就像无法进入这两个绕组，只能沿着这两个绕组的边缘(两个绕组本身的漏磁通磁路)通过。

3.2 直轴瞬变电抗

同样按照2.2节提出的新方法，直轴瞬变电抗的计算结果如下，各波形参见图3。

图3 直轴瞬变电抗有限元分析结果

定子机端相电压有效值:3 810.6 V

定子稳态相电流有效值:5 052.1 A

直轴超瞬变电抗实际值:0.754 2 Ω

直轴超瞬变电抗标幺值:0.129 9

从图3(c)可以发现，在瞬态瞬变时刻，由于阻尼绕组衰减完毕(等效于开路)，只有励磁绕组维持其磁链不变，感应电流，产生反磁链，去抵消电枢磁通;从磁力线图上来看，电枢磁通进入转子部分要比超瞬态时明显增加，但由于励磁绕组反磁链的影响，仍有较多电枢磁力线不经过转子闭合。

3.3 结果对比分析

将传统磁路法的计算结果与笔者提出的新方法的计算结果列表对比与表1。

考虑到有限元分析能较为准确的反映电机内部各个区域的饱和情况，而传统磁路法考虑饱和情况则略显粗糙，所以两种方法的计算结果会存在偏差。通过结果对比可知，笔者提出的新方法的计算结果与传统磁路法的计算结果接近，但数值略小。

表1 计算结果对比列表(标幺值)

4 结语

同步电机的瞬态和超瞬态电抗对电机的瞬态运行性能有着重要的影响。因此，应采用基于磁场的分析方法提高瞬态、超瞬态电抗的计算精度。

笔者提出一种基于二维瞬态电磁有限元分析，求取同步电机瞬态、超瞬态电抗的方法。该方法首先概念清晰、明确，可以得到瞬态、超瞬态瞬变时刻的磁场分布;其次计算精度较高，能得到较为准确的结果;而且通用性强，无论对于传统的同步电机、永磁同步电机还是采用实心磁极代替阻尼条的凸极同步电机，都可以采用这种方法方便的模拟超导体回路，从而计算瞬态、超瞬态电抗。

［1］Fuchs，E.F.，Erdelyi，E.A.:Determination of Waterwheel Alternator Transient Reactances from Flux Plot，IEEE Trans.，Vol-Pas-91，pp.1975-1802，Sept./Oct.，1972.

［2］Ashtiani，C.N.，Lowther，D.A.:Simulation of the Transient and Subtransient Reactances of a Large Waterwheel Generator by Finite Elements，IEEE Trans..Vol-PAS-103.Na 7，pp.1788-1794，1984.

［3］王建设，汤蕴璆.凸极同步发电机运算电抗频率特性及饱和瞬态电抗的有限元计算［J］.哈尔滨电工学院学报，1986(3).

［4］汤蕴璆，梁艳萍.二维正弦时变电磁场的串联约束问题［J］.哈尔滨电工学院学报，1995(2).

［5］高景德，王祥珩，李发海.交流电机及其系统的分析(2版)［M］.北京:清华大学出版社，1995.

［6］梁艳萍，汤蕴璆.水轮发电机瞬态电抗的数值计算［J］.电工技术学报，1996，11(6):2-26.

［7］梁艳萍，周封.用时步有限元法计算汽轮发电机直轴瞬态参数［J］.电机与控制学报，1998，2(2):69-74.