一类分数阶微分方程的广义拟线性化方法

王培光，侯颖，刘静

（1.河北大学 电子信息工程学院，河北 保定 071002；2.河北大学 数学与计算机学院，河北 保定 071002）

E-mail：pgwang＠hbu.edu.cn

研究报告

一类分数阶微分方程的广义拟线性化方法

王培光1，侯颖2，刘静2

（1.河北大学 电子信息工程学院，河北 保定 071002；2.河北大学 数学与计算机学院，河北 保定 071002）

采用广义拟线性方法讨论了Caputo分数阶微分方程初值问题，给出2个单调迭代序列，证明它们一致且平方收敛于方程的解.

分数阶微分方程；广义拟线性化方法；平方收敛

近年来，由于分数阶微分方程可描述现实世界的许多问题，其理论及性质已被广泛地应用于物理学、生物学等领域中，因而引起了人们的广泛关注［1-5］.

拟线性化方法［6］是研究微分方程定性问题的方法之一，在特定的条件下，可通过构造上、下解逐步逼近微分方程的解，保证了线性方程解的单调序列的平方收敛.本文通过使用广义拟线性方法，得到了Caputo分数阶微分方程

解的单调序列的平方收敛的结果.其等价的Volterra分数阶积分方程为

其中f∈C［J，R］，J＝ ［t0，T］，0＜q＜1，Γ为 Gamma函数.对于Caputo线性分数阶微分方程

其中g∈Cq［J，R］，且对q为 Hölder连续，其唯一解

E-mail：pgwang＠hbu.edu.cn

分别是含1参数和2参数的Mittag-Leffler方程.

首先给出如下定义及引理.

定义1 若存在α，β∈Cq［J，R］且满足

则称α（t），β（t）分别是式（1）的下解和上解.

引理1［7］令α，β∈Cq［J，R］分别为式（1）的下解和上解，且

当α（t0）≤β（t0）时，有α（t）≤β（t），t∈J.

引理2 令α，β∈Cq［J，R］分别为式（1）的下解和上解，α（t）≤β（t），t∈J，且f∈C［Ω，R］，Ω＝［（t，x）∶α（t）≤x≤β（t），t∈J］，则存在式（1）的解x（t）满足

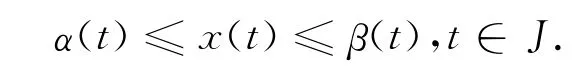
证明令P∶J×R→R且P（t，x）＝max［α（t），min（x，β（t））］，则f（t，P（t，x））是f在J×R上的连续扩张.由于f（t，x）在Ω上有界，则f（t，P（t，x））在 Ω上也有界.因此

定理1 假设

1）α0，β0∈Cq［J，R］为式（1）的下解和上解，α0（t）≤β0（t），t∈J；

2）f∈C［Ω，R］，fx，fxx存在且连续，且存在φ∈C［Ω，R］，φx，φxx存在且连续，并满足φxx＞0，fxx＋φxx≥0，则存在单调序列｛αn（t）｝和｛βn（t）｝一致且平方收敛于式（1）的解.

证明由2）可知，当α0（t）≤x2≤x1≤β0（t）时，有

其中F（t，x）＝f（t，x）＋φ（t，x），u（t0）＝x0＝v（t0），α0（t0）≤x0≤β0（t0）.由1）与式（6）得

由定义1知，α0，β0分别为式（7）的下解和上解.由式（6）及中值定得知，g（t，u；α0）满足

因此由引理2知，存在式（7）的解α1（t）使得

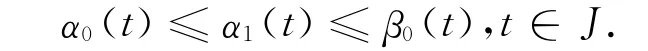
同理可得，α0，β0分别为式（8）的下解与上解且存在式（8）的解β1（t），使得

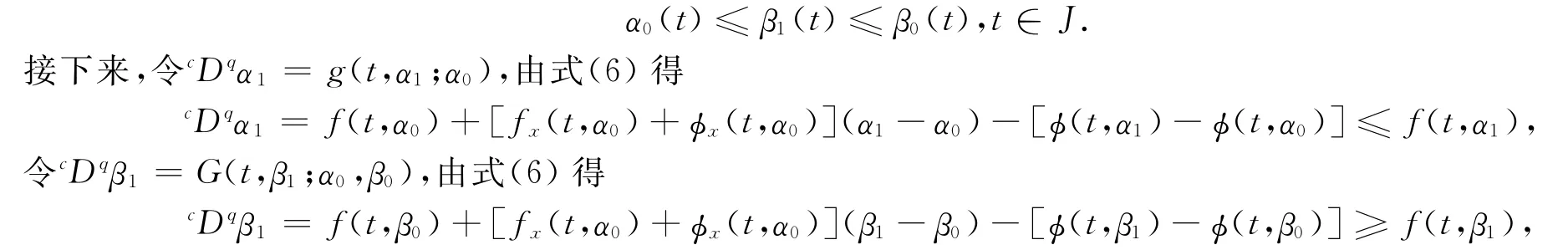
由定义1知，α1，β1分别为式（1）的下解与上解.因此由式（5）及引理1有

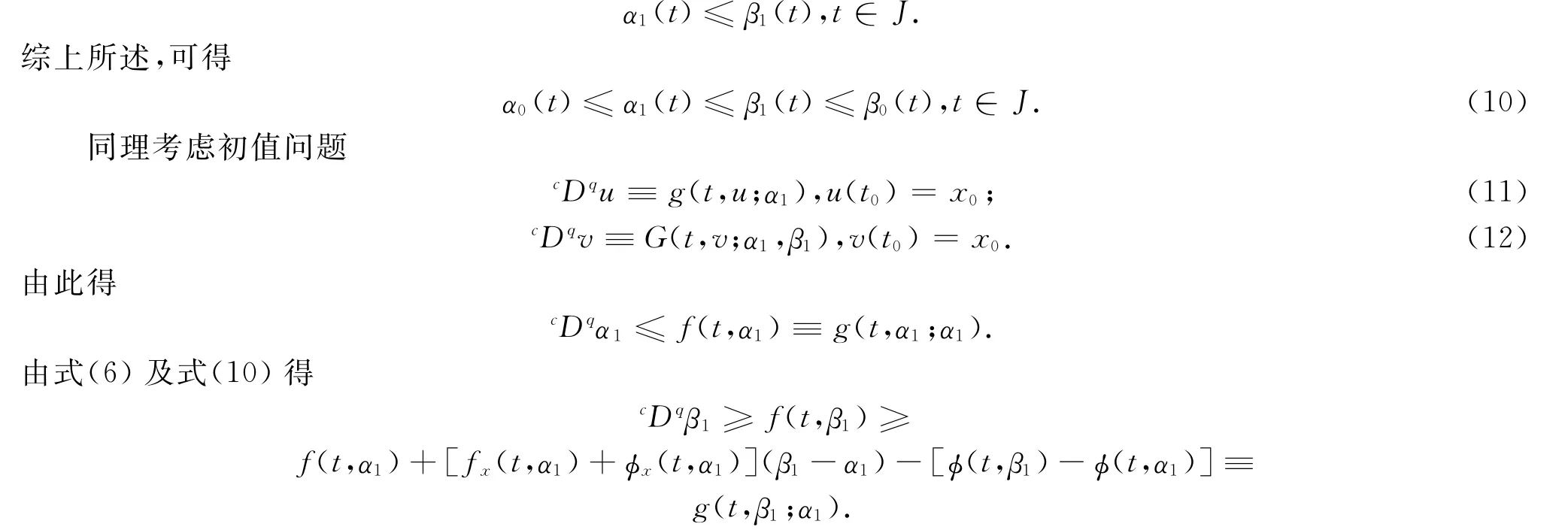
由定义1知，α1，β1分别为式（11）的下解与上解.因此，由式（9）及引理2得，存在式（11）的解α2（t）使得

同理，α1，β1分别为式（12）的下解和上解且存在式（12）的解β2（t）使得

其中α1≤σ≤β1.由定义1知，α2，β2分别为式（1）的下解与上解.因此，由式（5）及引理1有

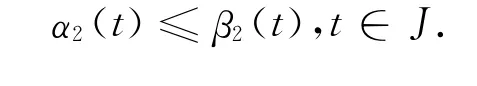
的解.综上可知序列｛αn（t）｝，｛βn（t）｝单调且一致收敛于式（1）的解x（t），t∈J.

下证序列｛αn（t）｝，｛βn（t）｝平方收敛于式（1）的解x（t）.假设

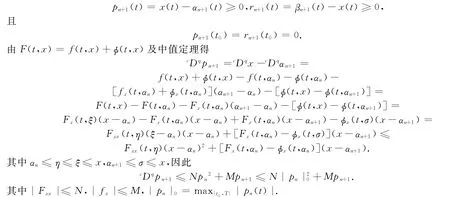
由Caputo线性分数阶微分方程（2）的解（3）及（4）的形式可得

［1］CAPUTO M.Linear models of dissipation whose Q is almost independentⅡ［J］.Geophys J R Astron，1967，13（5）：529-539.

［2］DIETHELM K，FORD N J.Analysis of fractional differential equations［J］.J Math Anal Appl，2002，265（2）：229-248.

［3］PODLUBNY I.Fractional differential equations［M］.San Diego：Academic Press，1999.

［4］GLÖCKLE W G，NONNENMACHER T F.A fractional calculus approach to self simslar protein dynamics［J］.Biophys J，1995，68（1）：46-53.

［5］KIRYAKORA V.Generalized fractional calculus and applications［M］.New York：LongmanWiley，1994.

［6］LAKSHMIKANTHAM V，VATSALA A S.Generalized quasilinearization for nonlinear problems［M］.Dordrecht：Kluwer Academic Publishers，1998.

［7］VASNUDHARA D J，MCRAE F A，DRICI Z.Generalized quasilinearization for fractional differential equations［J］.Comp Math Appl，2010，59（3）：1057-1062.

Generalized Quasilinearization for Fractional Differential Equations

WANG Pei-guang1，HOU Ying2，LIU Jing2
（1.College of Electronic and Information Engineering，Hebei University，Baoding 071002，China；2.College of Mathematics and Computer Science，Hebei University，Baoding 071002，China）

This paper employs the generalized quasilinearization method for initial value problems of Caputo fractional differential equations，and constructs two monotone sequences，then proofs both of them converge uniformly and quadratically to the solution of the equation.

fractional differential equations；generalized quasilinearization；quadratic convergence

O 175.1

A

1000-1565（2011）05-0449-04

2010-12-07

国家自然科学基金资助项目（10971045）；河北省自然科学基金资助项目（A2009000151）

王培光（1963-），男，黑龙江哈尔滨人，河北大学教授，博士生导师，主要从事微分方程与控制理论方面的研究.

王兰英）