现代轧钢技术轧机扭振的非线性研究

杜 勇，吴晓铃

（郑州大学 机械工程学院，河南 郑州 450001）

0 引言

随着现代轧钢技术的发展，人们对轧钢设备工作的稳定性以及轧钢产品的质量提出了更高的要求，而轧机主传动工作的稳定性与轧制生产的安全性及轧件的质量有着直接的关系。 轧机的主传动系统可看成弹簧质量系统，它由主电机、轧辊、联轴器、减速器、齿轮座和连接轴等部件构成，电机、轧辊、联轴器、减速器和齿轮座为惯性元件，连接轴等可视为弹性原件[1]。 在轧制生产过程中，抛钢、咬钢等轧制行为会造成主传动系统的载荷突变，常常会使其出现扭振现象，系统的扭振会造成轧辊工作不稳定，影响产品的质量，当振动过于强烈时，甚至还会导致轧制设备损坏，影响生产安全。 以往在研究系统的振动时，往往将其当作线性模型来处理，而实际生产过程中往往存在大量的非线性因素，所以这样的近似处理是不准确的[2-3]。 为此，笔者在考虑系统非线性因素的情况下，建立了轧机主传动系统的2 自由度非线性扭振模型， 利用近似解析法中的多尺度法，求出了系统共振时的一阶近似解，并通过Matlab 软件仿真得到了系统的幅频响应曲线， 分析了非线性阻力和非线性刚度对系统稳定性的影响。

1 轧机非线性扭振模型

1.1 模型图示

为便于分析计算，可将轧机主传动系统简化为2 自由度非线性扭振模型，其模型如图1 所示。

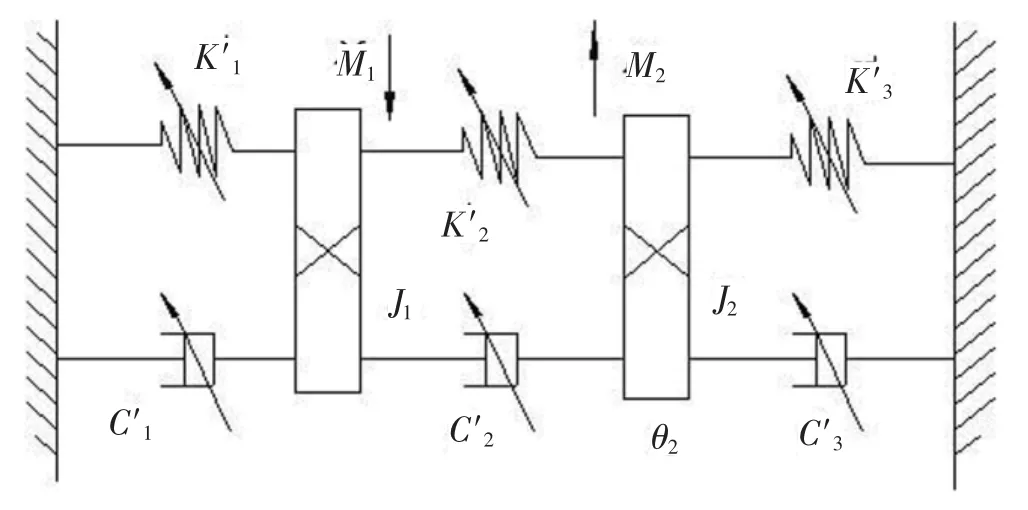
图1 轧机主传动系统2 自由度非线性扭振模型Fig.1 Two-freedom nonlinear torsional vibration model of mill main drive system

图1中，M1，M2为作用在左右轧辊上的等效轧制力矩，J1，J2为轧辊的等效转动惯量，θ1，θ2为轧辊轧制时轧辊的扭转角位移，k1，k3为轧辊与主电机间的等效扭转刚度，c1，c3为轧辊与主电机间的等效阻尼，c2'为两轧辊间的等效阻尼。

1.2 相关计算

考虑系统的非线性因素，利用Duffing 振子定义系统的非线性刚度、Vanderpol 振子，来定义系统的非线性阻尼[4]，因此有， k'1=k1+Δkθ21，k'2=k2+Δk(θ1-θ2)2，k'3=k3+Δkθ22，c'1=c1+Δcθ21，c'2=c2+Δc (θ1-θ2)2，c'1=c1+Δcθ21，由机械振动学理论，笔者可得该系统的运动方程：

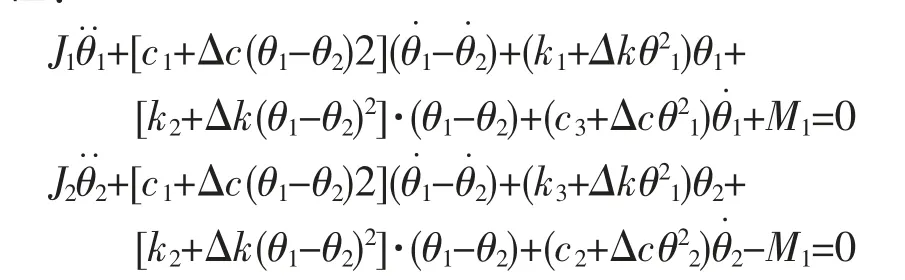
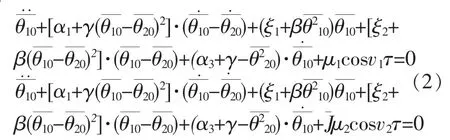
为方便求解，可将主传动系统看成近似的左右对称结构，因此有：J1=J2，c'1=c'3,k'1=k'3,M1=M2。 可只考虑系统左辊的振动行为，振动方程可简化为：

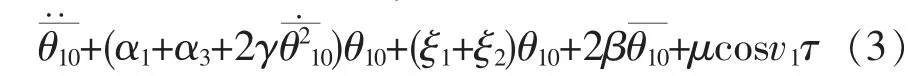
令θ10=x，α1+α3＝α，ξ1+ξ2＝ω2，v1=v，τ＝t，则式（3）可转化为：

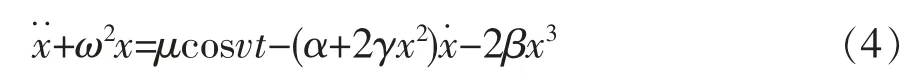
由机械振动理论可知，系统的固有频率ω 接近外界激励角频率ν 时，产生的共振现象称为主共振；系统的固有频率ω 接近外界激励角频率υ 的整数倍或者分数倍时产生的共振现象，称为次共振[5]。 据此可对系统的主共振和次共振现象进行分析。

2 系统共振区求解

2.1 主共振求解

采用多重尺度法进行求解，设ε 为小参数，δ 为频率调制参数。 主共振为当参激频率ν 接近固有频率ω 的振动，所以令：

引入不同尺度的时间变量：

又有非线性振动中不同尺度时间变量的函数:

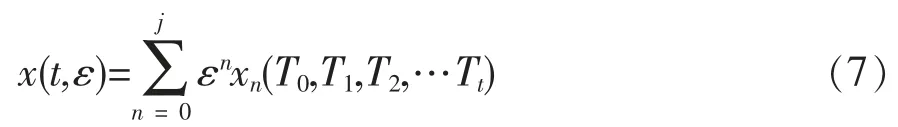
将式（7）对时间的微分按ε 的幂次展开，如下：

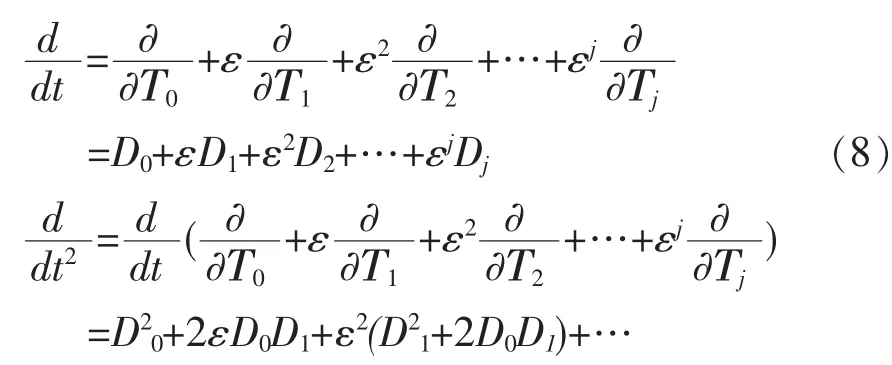
只讨论方程的一次近似解，可令:

将式（9）代入方程（4），并将其展开，可得：

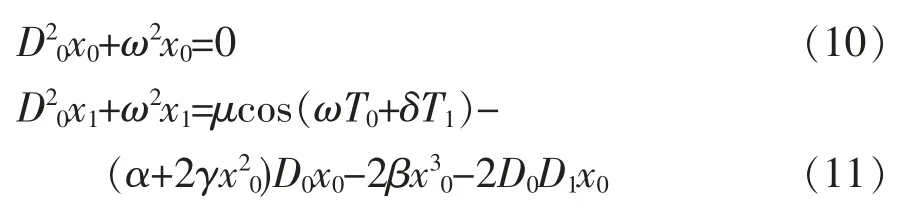
设式（11）的解为：

将式（12）代入式（11）的右边：

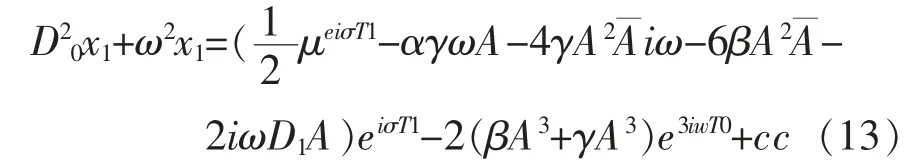
式（13）中cc 代表前面项的共轭复数，为避免出现久期项，要求函数A 满足：

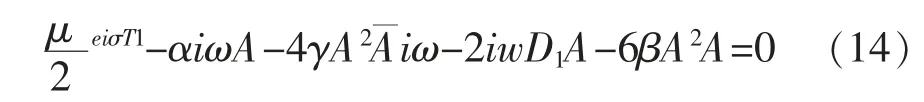
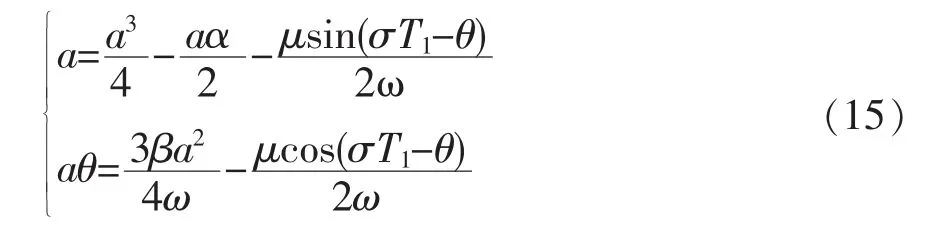
由式（15）可得主共振一阶近似解：

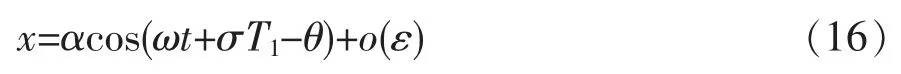
令α=0，θ=0，可得主共振的幅频关系式为：

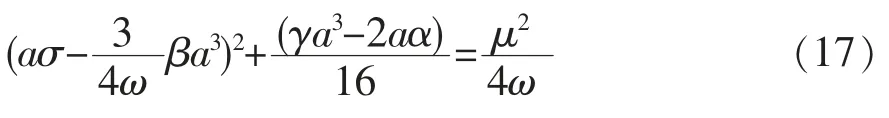
2.2 次共振求解

2.2.1 超谐波共振

将方程（4）的右边冠以小参数ε，将式（8）代入方程，可得：

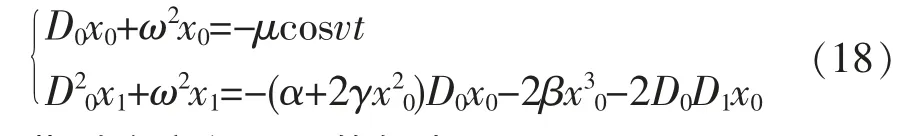
此时令方程（18）的解为:

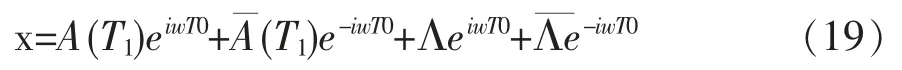
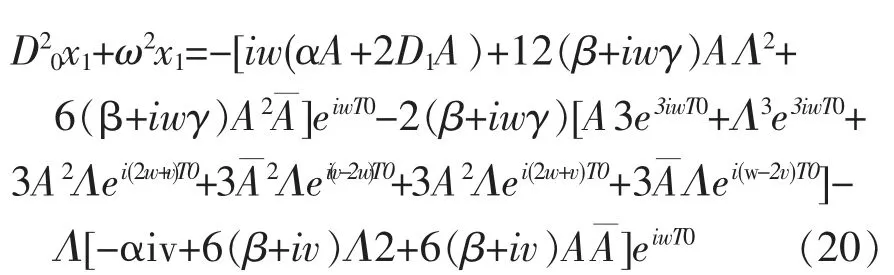
将式（21）代入式（20）右边含e3iwT0的项，并令右边含e3iwT0项的系数为零，来消除久期项有：

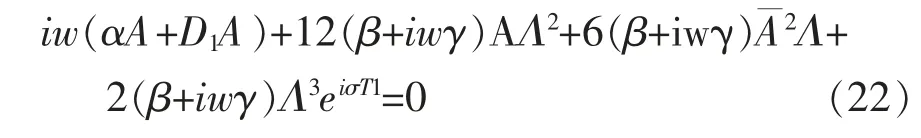
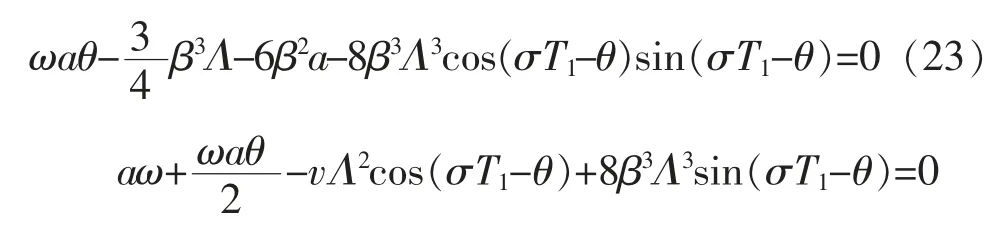
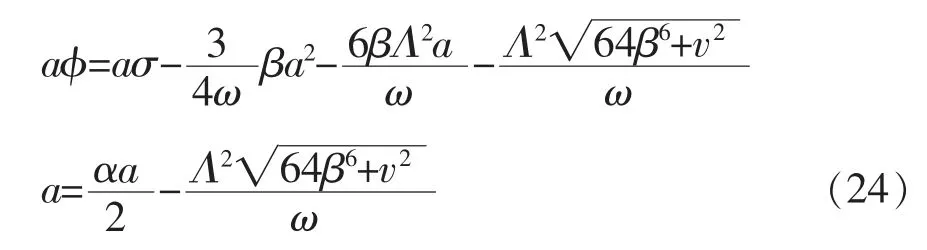
令a=0，φ=0, 得到超谐波共振的幅频特性曲线方程为：

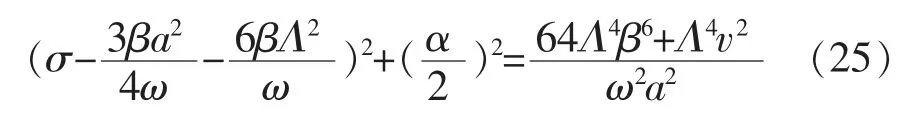
由式（24）可得超谐波共振的一阶近似解：

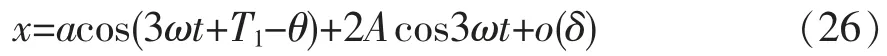
同样，可导出a、φ 的常值解as，φs应满足：

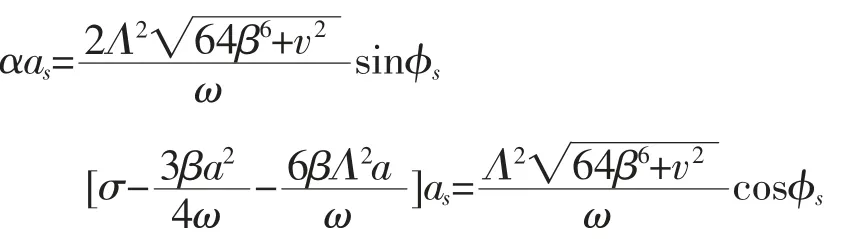
2.2.2 亚谐波共振

当v≈3ω 时，系统产生亚谐波共振，此时设v 与3ω 的差值为ε 的同阶小量，即：

将式（28）代入式（20）右边含ei(v-2ω)T0的项，并令eiωT0的系数为零，消除久期项，可得到：

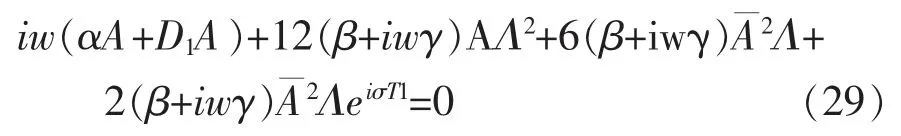
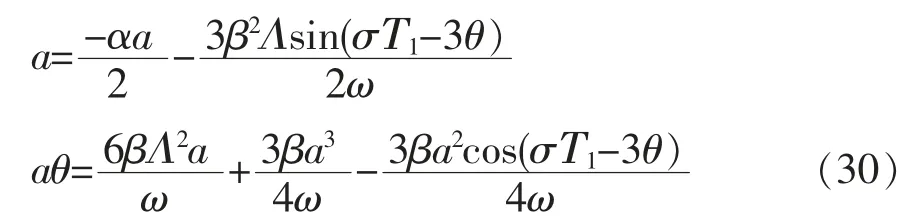
令φ＝σΤ1-3θ，式（30）可化为：

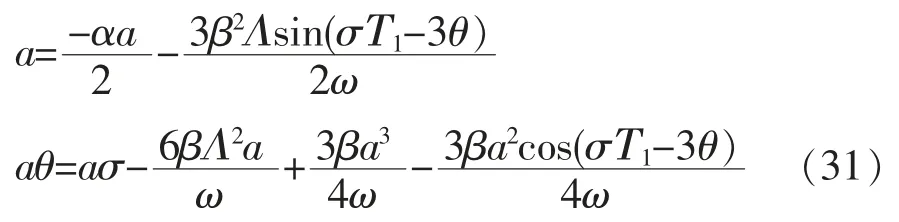
则亚谐波共振的一阶近似解为：

导出亚谐波下的幅频响应特性曲线：

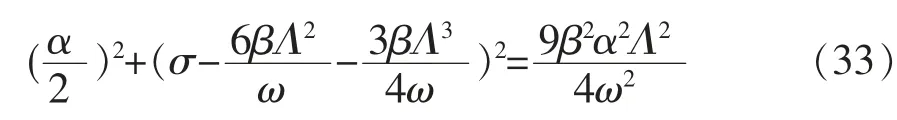
3 数值仿真

根据4 200 中厚板轧机的实际物理参数值，经过计算，取下列参数的近似值，分别为：α1=0.0053，α2=0.012，α3=0.046，β=0.2，γ=0.005，μ=0.008。

根据这些参数值和主共振下的频率方程式（17），利用Matlab 进行编程仿真，其系统幅频特性曲线如图2 所示。

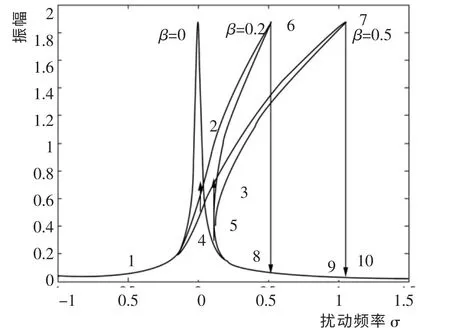
图2 非线性刚度β 变化时的主共振幅频响应曲线Fig.2 Main resonance amplitude-frequency response curve of nonlinear stiffness β changes

图2为主共振在非线性刚度β 变化时系统的幅频响应曲线。从图中可以看出，随着非线性刚度β 增大，频率响应曲线向右偏移，且β 越大，偏移越明显。当β 取0.2 和0.5 时，均出现跳跃区域（β=0.2 时的跳跃区域为点2、4、6、8 围成的区域， 而点3、5、7、10构成的区域为β=0.5 的跳跃区）。 从图中还可以看出，扰动角频率逐步增大时，幅值大小会发生变化：当β=0.2 时，其幅值按照1-2-6-8-10 的路线变化；当到点6 时，发生突跃，直接到点8；β=0.5 时，幅值变化路线则为1-3-7-9-10,7、9 两点间有跳跃。 当扰动频率发生从大到小的变化时，β=0.2 的幅值变化路线为10-8-4-2-1，点4 向点2 跳跃，β=0.5 的幅值则按10-9-5-3-1 的路线变化，点5 跳跃到点3。当β=0 时，即系统无非线性刚度，图2 中幅频曲线无偏移、无跳跃。 这说明系统的振荡仅仅与非线性刚度相关，与线性刚度、非线性阻尼、线性阻尼等均无关。 幅频曲线偏移量越大，则幅值跳跃差值越大，系统振荡越厉害。 由此可知，非线性刚度会引起系统振荡，并且随着非线性刚度的增大，其振荡更为明显，而振荡会影响轧机传动系统的稳定性。

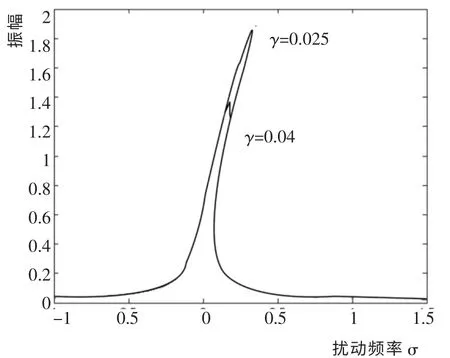
图3 非线性阻尼γ 变化时的主共振幅频响应曲线Fig.3 Main resonance amplitude-frequency response curve of nonlinear damping γ changes

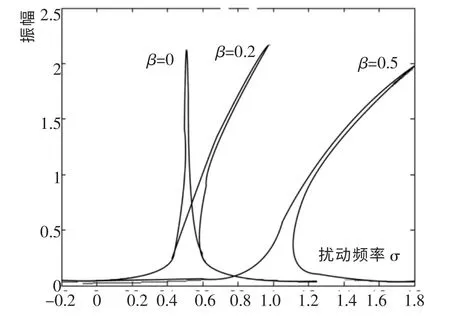
图4 非线性刚度β 变化时的超谐波幅频响应曲线Fig.4 Ultraharmonic amplitude-frequency response curve of nonlinear stiffness β changes

图3 是非线性阻尼γ 变化时的主共振幅频响应曲线。 从上述图2 分析可知，幅频曲线的跳跃仅与非线性刚度相关，所以从图中不难知道，随着非线性阻尼γ 的增大，振幅减小。

由于式（32）超谐波频率响应方程中未含非线性阻尼项，这里只需考察非线性刚度的影响。由图4可知，当非线性刚度β=0 时，曲线无偏移，这说明在超谐波情况下，系统的振动仍然只同非线性刚度有关，随着β 的增大，幅频曲线有偏移，且存在跳跃，即系统存在振动。3 条曲线振幅的最大值近似相等，这表明，非线性刚度对振幅幅值没有多大的影响。

图5 为亚谐波共振下非线性刚度β 变化时的频率响应曲线。 亚谐波的情况与超谐波一样， 方程（32）不含非线性阻尼项，故只需考虑非线性刚度。从图中可以看出， 非线性刚度β 使频率响应曲线向右偏，因此存在振动，而且随着β 的增大，振幅幅值减小，偏移量增大。

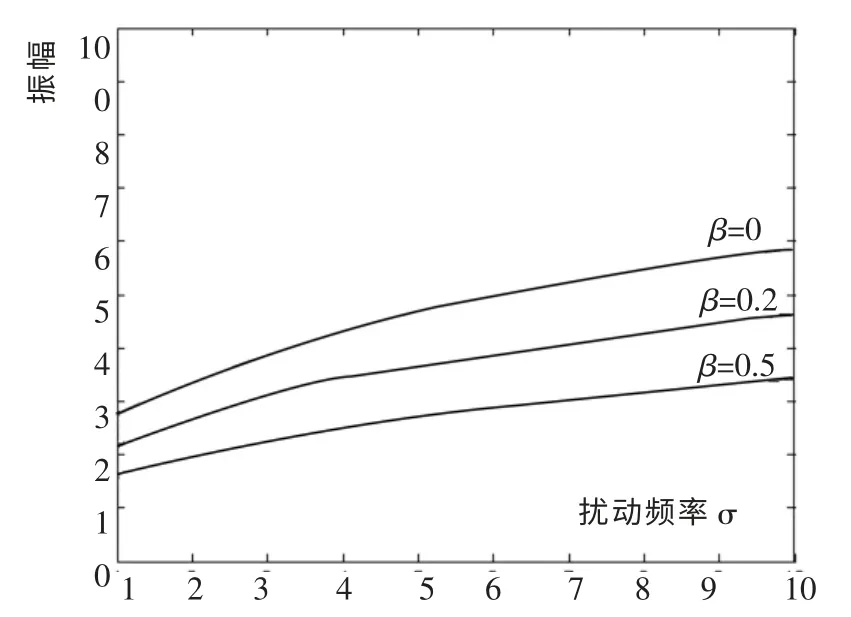
图5 非线性刚度β 变化时的亚谐波幅频响应曲线Fig.5 Subharmonic amplitude-frequency response curve of nonlinear stiffness β changes

4 结论

综上所述，本文建立了2 自由度轧机主传动系统非线性扭振模型，参考系统振动过程中的非线性因素，发现共振幅频响应曲线的偏移只与非线性刚度有关，非线性阻尼影响振幅的幅值。 非线性刚度值越大，偏移越厉害，系统振荡越强烈，系统也越发不稳定，对轧机主动系统的危害越大。

[1] 邹家祥，徐乐江. 冷连轧机系统振动控制[M]. 北京：冶金工业出版社，1998:1-200.

[2] 林鹤，康祖立.初轧机轧制打滑引起的扭振响应[J].北京科技大学学报，1991，13(1)：31-36.

[3] Farley, Tom. Mill vibration during cold rolling [J]. MPT Metallurgical Plant and Technology International, 2007,30(1)：62-66.

[4] 陈勇辉，史铁林，杨叔子. 四辊冷带轧机非线性参激振动的探究[J]. 机械工程学报.2003,39（4）：56-60.

[5] 刘延柱，陈立群. 非线性振动[M]. 北京：高等教育出版社，2001：88-92.