基于强度折减法的露天矿边坡稳定性分析＊

洪 勇 李克民 孙会朝 王天才 周 伟

(1.中国矿业大学矿业工程学院,江苏省徐州市,221008;(2.煤炭资源与安全开采国家重点实验室,江苏省徐州市,221008)

基于强度折减法的露天矿边坡稳定性分析＊

洪 勇1,2李克民1,2孙会朝1,2王天才1,2周 伟1,2

(1.中国矿业大学矿业工程学院,江苏省徐州市,221008;(2.煤炭资源与安全开采国家重点实验室,江苏省徐州市,221008)

基于有限元强度折减理论,使用phase2数值模拟软件模拟分析露天矿边坡的稳定性,结果表明,通过对岩体边坡模型进行强度折减,边坡体塑性区从坡顶至坡底贯通时边坡体破坏,故认为折减系数即边坡的安全系数,在数值模拟中则表现为计算的不收敛性,为露天矿山生产准确判断边坡体的破坏和确定安全系数具有实际的指导意义。

露天矿 边坡稳定 强度折减法 数值模拟

边坡稳定性分析是边坡设计的前提。边坡稳定性的计算方法概括起来可以分为两大类:一种是传统的极限平衡法,另一种是数值分析方法。极限平衡法中常用的有瑞典圆弧法、毕肖普法、萨尔玛法。这些方法没有考虑岩体本身的应力-应变关系,对滑坡的边界条件进行了简化,而且需要事先知道滑动面位置和形状,这样在具体的工程实际中不能客观反映真实情况。目前,数值分析在边坡稳定计算中得到应用,且克服了传统极限平衡法的缺点,考虑了岩土体本身的应力-应变关系,为边坡的稳定性分析提供了更好的依据。本文以有限元的强度折减法理论为基础,对某露天矿边坡稳定性进行了数值模拟分析,为露天矿边坡的稳定性分析提供参考。

1 有限元强度折减法原理

有限元强度折减法计算边坡安全系数是从岩土边坡的各种实际情况出发,研究其在各种类型岩土中建模、求解的实际应用,已有很多对工程有益的结论。强度折减的基本原理是在理想弹塑性有限元计算中通过折减系数F不断调整边坡岩土体的强度参数粘聚力c和内摩擦角Φ,公式如下:

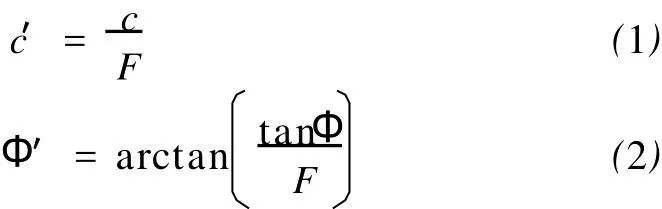
将调整后的c′,Φ′输入到模型进入试算,利用相应的边坡破坏判断准则,有限元程序根据计算自动得出边坡破坏面,计算出对应的折减系数F称之为边坡体的最小安全系数。结合摩尔库伦准则,由式(1)和(2)可得:

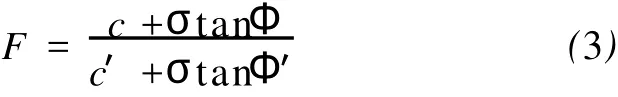
式中:c、c′——折减前后的粘聚力;

Φ、Φ′——折减前后的内摩擦角;

σ——正应力;

F——折减系数。

可以看出,强度折减法的本质与极限平衡法一致,反映的都是实际强度与极限平衡时的强度之比。运用有限元强度折减法进行计算的基本思路是:首先选择材料的屈服准则,然后确定其服从的流动法则,进而得出其塑性势函数,然后确定其硬化规律。本文中岩土设为理想弹塑性材料,故其硬化参数为零,最后根据选定的破坏判据得出边坡破坏的最终结果。

2 强度屈服判别准则及流动法则的选用

岩土工程的数值分析离不开岩土材料的本构关系,而研究材料的本构关系首先要建立其产生屈服与破坏的条件和判别准则。本文中本构关系选用理想弹塑性模型,屈服准则选用摩尔-库伦准则,在平面应力状态下可表示为:

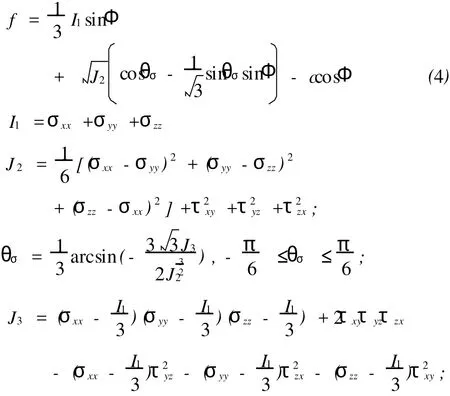
式中:I1——第一应力不变量;

J2——第二应力偏张量;

J3——第三应力偏量不变量;

θσ——洛德角。

对土体进行弹塑性有限元分析时,若应力处于包络线以内,即f<0,则该区域处于弹性状态;若应力处于包络线上,即f=0,则该区域处于极限状态;若应力处于包络线以外,即f>0,则该区域处于屈服状态,应力需进行修正。

在边坡计算过程中,采用非关联或者是关联流动法则取决于剪胀角,当采用关联法则时,剪胀角φ=Φ,当采用非关联法则时,剪胀角φ=0,通过近几年的研究表明,采用关联流动法则较之非关联流动法则计算结果偏大,本文中计算采用非关联法则。

3 边坡破坏的判据

当一种材料进入到无限塑性状态时称之为破坏,数值计算判断边坡体破坏通常有以下3种:

(1)有限元解的数值计算不收敛;

(2)边坡内塑性区或者塑性应变从坡底到坡顶相互贯通,此时折减系数即为边坡体的安全系数;

(3)滑动体的滑动,即特征点的位移突变,认为边坡体达到了临界失稳状态。

强度折减法有限元方法中采用解的不收敛作为边坡体失稳的判断依据,上述三种破坏标准有如下关系:有限元解的不收敛时意味着塑性区的贯通和位移的突变,即上述(2)、(3)两条,然而塑性区的贯通只是边坡体破坏的必要条件,还需进一步观察其位移和应变的大小,这就是结合(3)条所述的最后导致边坡体的无限滑动,从而判定此边坡体破坏。因此本文中将有限元的解是否收敛作为边坡体破坏的依据。

4 露天矿边坡稳定性实例分析

4.1 工程概况

该边坡为某露天煤矿首采区边坡,该露天矿地处剥蚀堆积地形与低缓丘陵地形过渡地带,首采区位于露天矿东南部,目前采深约为70 m,共有三层,从上到下模型中分别命名为A1、A2和A3,各地层及主要岩土参数见表1,模型的尺寸见图1,计算软件采用罗赛斯(Rocscience)公司的Phase2软件6.0版进行模拟。

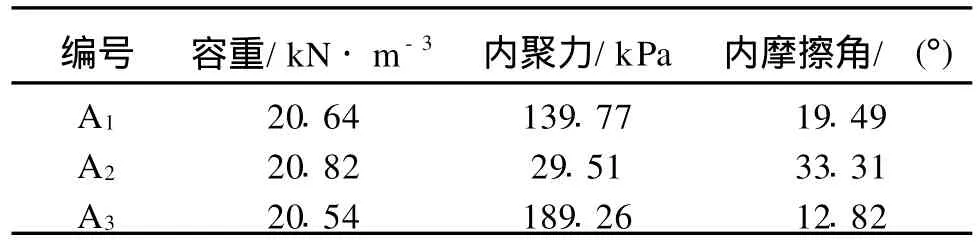
表1 岩土力学参数

4.2 模型的建立

根据几何尺寸在Phase2中输入模型的边界,网格采用六节点三角网格,边坡的左侧和底部施加x,y方向的约束,上面为自由面,所受荷载主要是自重,施加重力加速度,按照表1输入不同岩层的岩石力学参数,材料特性采用弹塑性物理模型,屈服准则采用摩尔-库伦屈服准则,采用最大迭代次数500次作为边坡体失稳判断准则判据。模型中共包含1610个单元、3327个节点。

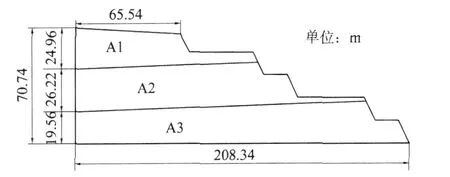
图1 模型几何尺寸

4.3 有限元计算结果

计算中初始折减系数为1,然后按折减系数0.01逐渐递增进行运算,折减系数计算精度为0.002。程序运行结束后,得到模型边坡的最大切应变图、位移图和收敛曲线图,并对相应的边坡模型进行应变分析、位移分析和收敛性分析。输出结果显示该露天矿目前采区边坡的临界强度折减系数为1.41,即该边坡的安全系数为1.41。

从边坡的最大切应变图反映出,边坡发生破坏时应力主要集中在第二层A2中,即边坡首先发生破坏的位置位于A2层的坡面上,而从边坡的最大位移图反映出,当折减系数为1.41时,A2层中台阶坡面塑性区贯通,此时坡面有向下和向采空区滑坡的趋势,另外从前面的收敛准则得出:当安全系数K=1.4时,最大位移为0.37 m;当安全系数K=1.41时,边坡处于极限平衡状态,此时边坡体的最大位移为0.38 m;而当安全系数K=1.42时,此时计算不收敛,此时的最大位移为0.48 m,位移突变,边坡体破坏。从现场观察的实际情况来看,A2岩层岩土属于软岩,岩体强度较低,而其设计的边坡角与其他岩层边坡角相同,随着时间的推移和开采深度的加深,其坡面已经出现了滑坡的迹象,台阶上出现裂缝,综合数值模拟分析的结果与现场实际观察的情况相符合。

5 结论

(1)强度折减法的优点体现在不需要事先假设滑动面的位置和形态,能得出滑动面的实际形态和滑动面的发展趋势,而且能确定边坡开挖前后的应力状态及其变化,通过phase2软件依次进行迭代计算取值,生成不同折减系数时的图像,以便分析边坡岩体的渐进破坏。

(2)强度折减系数本质上就是边坡体的安全系数,计算时解的不收敛为边坡破坏的判据,此时边坡体塑性区贯通,滑动面上位移产生突变,通过计算机模拟分析可以直观形象地显示出边坡体的滑动面。

(3)对非均质边坡体需进一步进行分析。本文中对于不同性质的岩土采用的折减系数是相同的,然而实际中不尽然,故对于不同性质的岩土进行多少系数的折减还有待探索。

[1] 孙玉科.中国露天矿边坡稳定性研究[M].北京:中国科学技术出版社,1999

[2] 姜兆华,李继祥,段文付.有限元强度折减法在边坡稳定性分析中的应用[J].武汉工业学院学报,2008(2)

[3] 曾亚武,田伟明.边坡稳定性分析的有限元法与极限平衡法的结合[J].岩石力学与工程学报,2005(2)

[4] 熊传治,杜维吾,彭状等.用有限元强度折减法求算边坡安全系数初探[J].矿冶工程,2008(2)

[5] 郑颖人,赵尚毅.有限元强度折减法在土坡与岩坡中的应用[J].岩石力学与工程学报,2004(19)

[6] 郑颖人,赵尚毅,宋雅坤.有限元强度法研究进展[J].后勤工程学院学报,2005(3)

[7] 赵尚毅,郑颖人,时卫民,王敬林.用有限元强度折减法求边坡稳定性安全系数[J].岩土工程学报,2002(3)

[8] 连镇营,韩国城,孔宪京.强度折减有限元法研究开挖边坡的稳定性[J].岩土工程学报,2001(4)

Slope stability analysis of open-pit mine based on strength reduction method

Hong Yong1,2,Li Kemin1,2,Sun Huichao1,2,Wang Tiancai1,2,Zhou Wei1,2
(1.School of Mines,China University of Mining and Technology,Xuzhou,Jiangsu 221008,China;2.National Key Laboratory of Coal Resource and Mining Safety,Xuzhou,Jiangsu 221008,China)

This article simulates and analysis an actual open-pit mine slope stability using the phase2 numerical simulation software,which is based on the finite element strength reduction theory,the results show that the reduction factor is the safety factor of slope,the strength reduction was determined through the model of the rock mass slope,slope body failure when the plastic zone developed from slope top to toe,which means the program non-convergence in the numerical simulation,this article have the practical significance which can accurate judge the failure of the slope body and determine the safety factor.

open-pit mine,slope stability,strength reduction method,numerical simulation

TD824.7

A

十一五国家科技支撑计划项目(2006BAB16B00);博士点基金项目资助(20100095110019);煤炭资源与安全开采国家重点实验室自主研究课题资助(SKLCRSM10X01);中央高校基本科研业务费专项资金资助(2010QNA33,2010ZDP01A02)

洪勇(1986-),男,湖南衡阳人,中国矿业大学矿业工程学院在读硕士研究生,研究方向露天开采。

(责任编辑 张毅玲)