碳纳米管增强镁基复合材料的界面分离特性
祝 杰, 李维学,, 戴剑锋,, 王 青,
(1. 兰州理工大学 物理系,兰州 730050;2. 兰州理工大学 甘肃省有色金属新材料省部共建国家重点实验室,兰州 730050)
碳纳米管增强镁基复合材料的界面分离特性
祝 杰1, 李维学1,2, 戴剑锋1,2, 王 青1,2
(1. 兰州理工大学 物理系,兰州 730050;2. 兰州理工大学 甘肃省有色金属新材料省部共建国家重点实验室,兰州 730050)
建立碳纳米管增强镁基复合材料界面弹性应力传递摩擦拔出模型,得到镁基复合材料各组分的应力和应变。考虑泊松效应和界面上摩擦应力的作用以及基于界面分离过程能量平衡和界面应变失配原则,得到界面能释放率和裂纹位移展开轮廓的表达式。分别从界面能释放率和裂纹位移展开轮廓两个方面研究复合材料性能参数对碳纳米管增强镁基复合材料断裂的影响。结果表明:界面分离长度和界面厚度较大,则复合材料的界面分离能释放率就越大;较大的界面分离长度、界面厚度、弹性模量和泊松比均对复合材料的裂纹位移展开轮廓产生较大影响;碳纳米管长径比越小,则复合材料的界面分离能释放率和裂纹位移展开轮廓越大;对界面材料的弹性模量和泊松比选择存在着最佳值。
碳纳米管;镁基复合材料;界面;能量释放率;裂纹位移展开轮廓
镁基复合材料以较高的比强度和比刚度、密度小、加工性能好等优点备受关注[1−2]。 碳纳米管也具有强度高、高刚度和弹性模量以及高韧性等优点,是增强镁基复合材料最理想的增强相之一[3−5]。因此,碳纳米管增强镁基复合材料已成为材料领域的研究热点。但是镁基复合材料在制造加工和应用过程中也出现了损伤、断裂、滑移和脱落等现象[6],带来了不安全因素。因此,研究镁基复合材料在载荷作用下的界面分离,成为研究者们十分关注的问题。研究表明:能量释放准则在材料断裂中有广泛的适应性。如 HSUEH[7]和OCHIAI等[8]获得了分离能释放率的解,然而由于忽略了纤维中剪切应力和应变能、基体轴向应力随位置的变化及泊松效应等具有一定缺陷。CHIANG[9]推导出包括纤维轴向应变能、基体轴向和剪切应变能在内的分离能释放率表达式。RAUCHS等[10]运用有限元法获得了能量释放率的数值解,然而过度的简化导致较大误差。JIANG等[11]利用Shear-lag模型导出了界面分离能释放率,然而在应力分析中却忽略了泊松效应、基体轴向应力和剪切应力对应力传递效率的影响。LIU[12]和刘鹏飞[13]分析了界面分离能释放率、临界分离应力和桥联本构关系对材料的影响。这方面的研究主要用试验方法、有限元法以及边界元法[14−16]。但裂纹奇异单元的存在,有限元和边界元法的计算结果误差较大。
复合材料在外加载荷下,界面分离区域内是伴随着复杂的滑移和摩擦作用的,会影响基体裂纹的展开程度。同时,界面材料各组分性能参数对裂纹能量释放率和裂纹扩展的影响的研究较少。基于以上考虑,本文作者根据弹性断裂理论,通过纤维拔出过程中界面分离弹性应力传递模型,得到了在界面分离和结合区域内纤维和基体的应力和应变。基于能量释放准则利用解析计算方法研究了界面材料不同性质对裂纹能量释放率的影响,得到了能量释放率随结构尺寸和材料性质变化情况;基于界面应变失配原则,导出Ⅱ型基体裂纹展开位移轮廓随结构尺寸、材料性质变化规律。
1 应力和应变分析模型
图1所示为CNTs在镁基体中的排列示意图。采用的模型为无限大基体中包含一定数量的纤维,假设碳纳米管在镁基复合材料中完全分散和取向一致,以六角形阵列排列。在复合材料受到外载荷破坏后,从模型中取出一个代表性体积元(RVE)进行分析,如图2所示。取出一个外径为a、嵌入外半径为R的同心基体中的单纤维并含有界面(外半径为b)的模型,嵌入镁基体中的CNTs长度为L,界面分离长度为Ld,在柱坐标系(rθz)中,z轴为纤维轴向,纤维加载端和嵌入端分别为z=0和z=L,纤维拔出应力σ平行于z轴;在距基体裂纹端x位置处,分离界面上伴随着复杂的摩擦滑移,纤维和基体在界面上的轴向位移差导致基体裂纹展开位移轮廓ux的产生。
图1 CNTs在镁基体中的排列示意图Fig.1 Schematic diagram showing CNTs arraying in Mg matrix
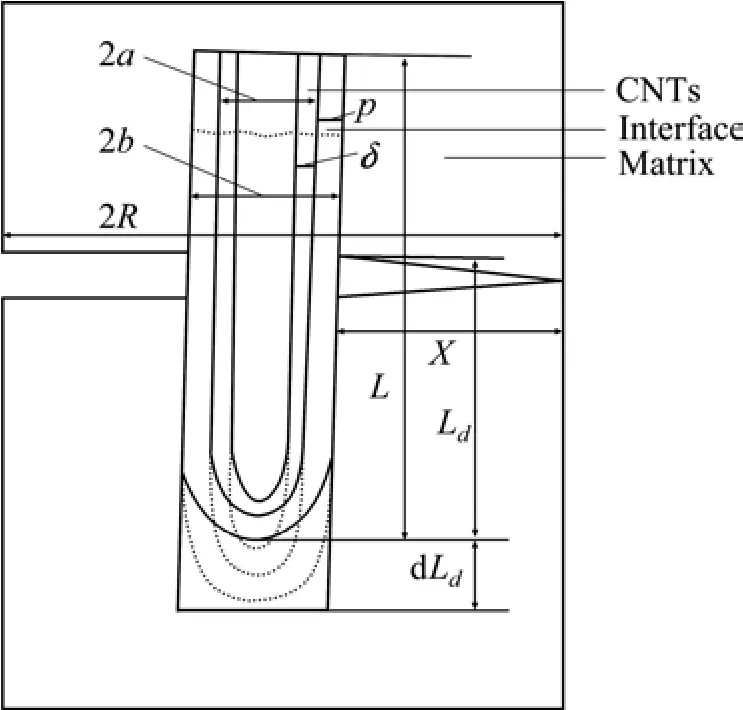
图2 拔出应力作用下分离界面上的摩擦滑移示意图Fig.2 Schematic diagram showing frictional sliding at debonded interface under pull-out stress
根据建立的模型,复合材料中CNTs的体积分数(φf)和界面的体积分数(φn)分别为

式中:φf是碳纳米管增强镁基复合材料中 CNTs的体积分数;φn是碳纳米管增强镁基复合材料中界面的体积分数;βR=R/a 是 RVE与 CNTs半径之比;βb=b/a是界面与CNTs半径之比;LLm/=χ是RVE 与CNTs长度之比。
在代表性体积元中取某一平行六面体,考虑其对称性和应力在z轴方向的平衡,在柱坐标系(rθz)中平衡方程式为

式中:r为沿模型径向的取值参数。
取某一微元体,在z轴方向上对各组分进行受力分析,得到平衡方程:
对于CNTs,

式中:τ1表示碳纳米管与界面之间的剪切应力,τ2表示界面与镁基体之间的剪切应力。表示各组分在z轴方向受到的平均应力。
根据弹性理论,结构单元体的本构方程为
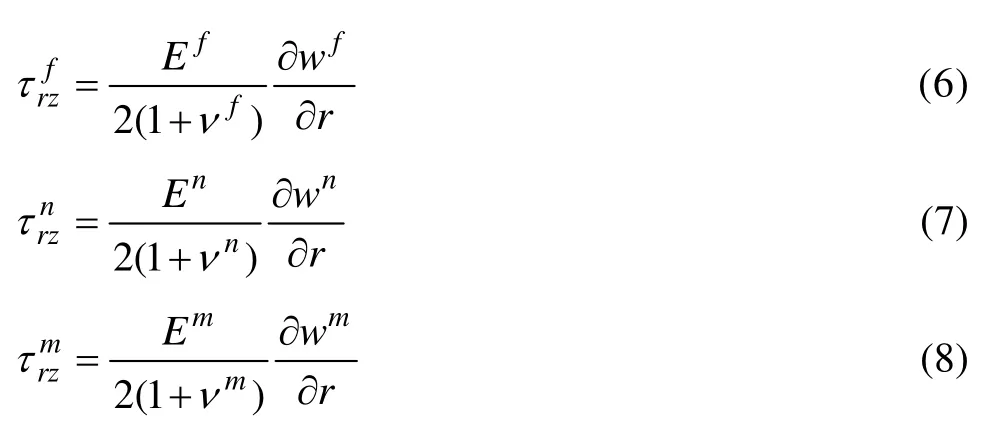
在均匀外载σ作用下,代表性体积元体几何变形的边界条件如下。
1) 界面的连续条件:

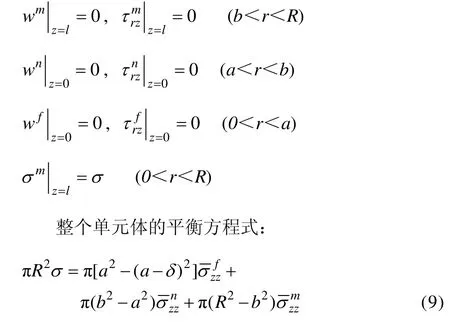
式中:δ表示多壁碳纳米管中万墨层的间距,一般δ=0.34 nm。
由式(2)~(8)以及边界条件,并对 r积分可得到各组分位移表达式:
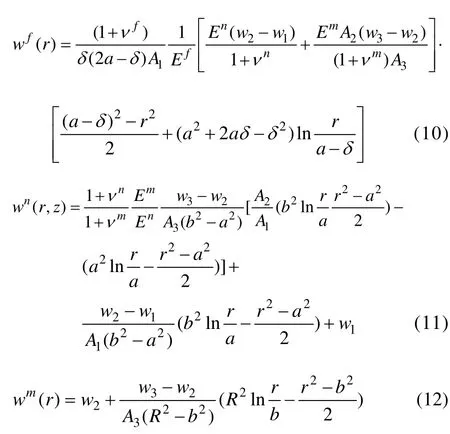

由剪切滞后方法分析得到单元体中各组分的应力控制方程:
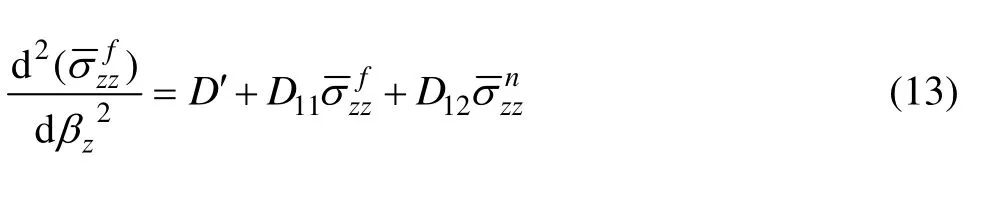

式中:βz=z/a、βR=R/a、βb=b/a;D′、D″、D11、D12、D21、D22是镁基复合材料中组分弹性模量之比(λi)的函数;λn=En/Ef;λm=Em/Ef为镁基复合材料性能常数,碳纳米管的横截面面积之比为

由式(13)和(14) 可解得单元体中各组分的轴向正应力与剪切应力:
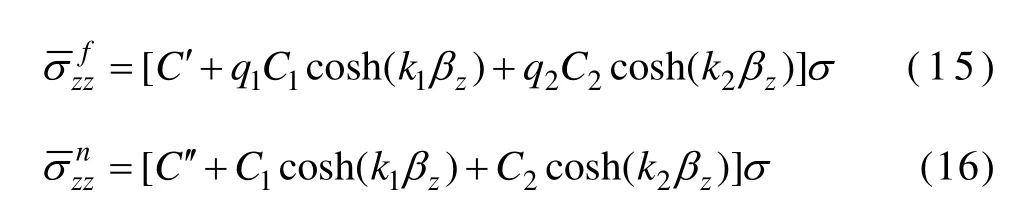

根据应变的定义:ε=dw/dz,可得到单元体中各组分的应变表达式如下:
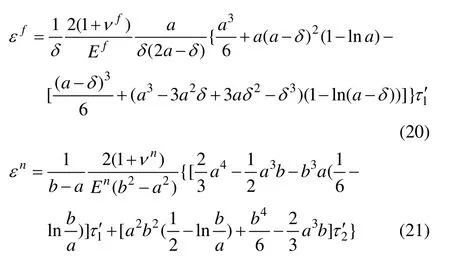
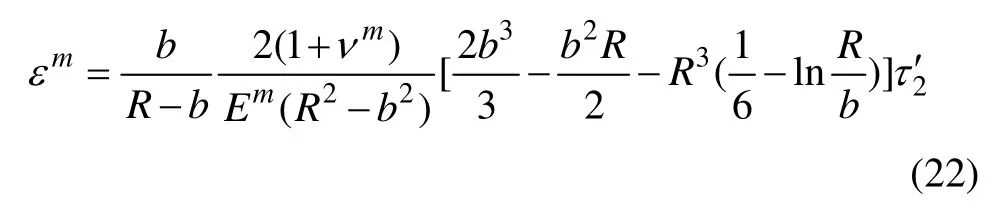
其中,
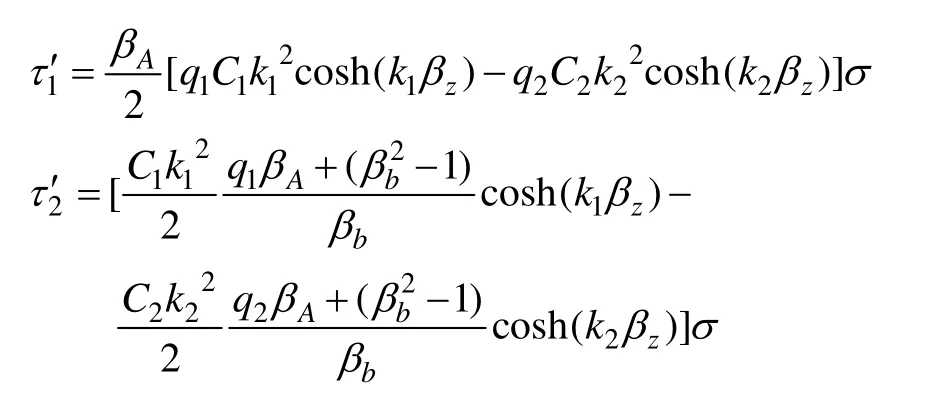
2 能量释放率与裂纹位移展开轮廓分析
2.1 界面能量释放率
根据能量平衡理论,裂纹扩展的条件是裂纹体在裂纹扩展过程中能释放出足够的弹性能,以供表面能增加的需要。按照断裂力学理论,界面分离可视为Ⅱ型裂纹扩展。在界面分离过程中,4个能量项应满足如下平衡关系:1) 纤维和基体储存的弹性应变能Ue;2) 拔出载荷作功Uw;3) 界面摩擦应力作功Uf;4) 当界面裂纹扩展长度为dLd时,分离界面上的表面能以dA=2πrdLd的因子增加,则表面能 dW=GdA。在不考虑热量交换的条件下,能量平衡关系为Uw=Ue+Uf+dW。其中,镁基复合材料的应变能可表示为
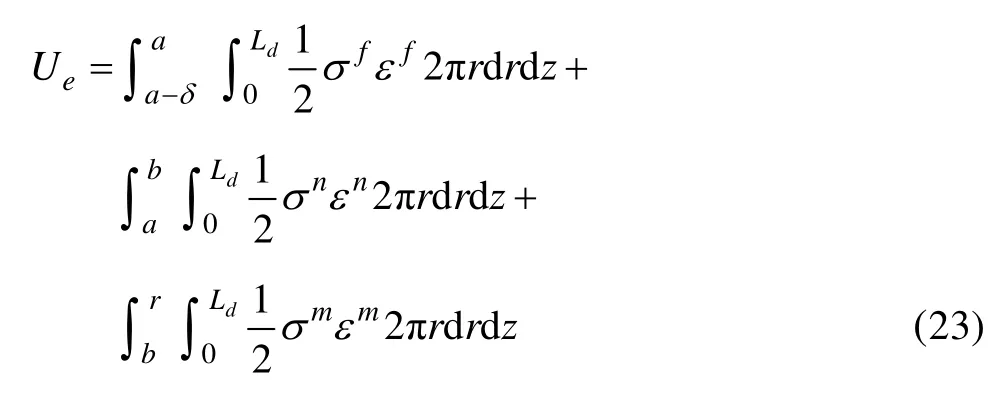
在含界面的 CNTs拔出过程中,界面分离区域L≤z≤Ld内,假设剪切应力τz退化为常摩擦应力,则复合材料的摩擦能为
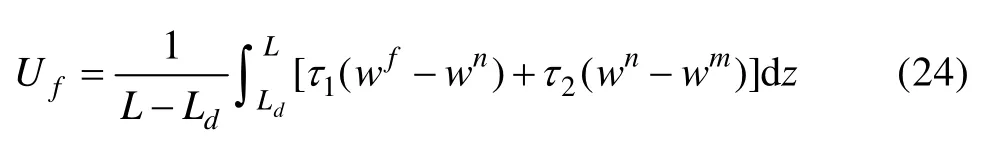
在远场外载荷下,外力在裂纹扩展中对系统所作的功为
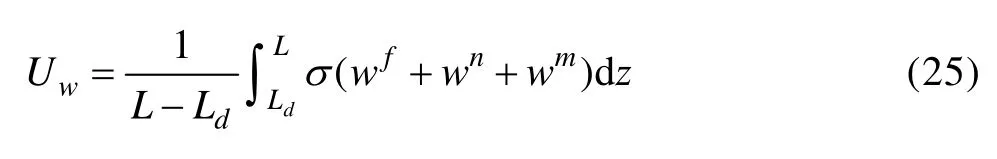
根据界面分离能释放率G的定义,其表达式可表示为
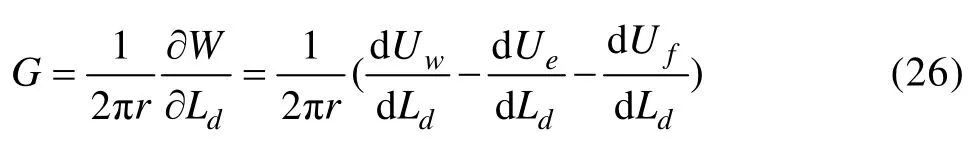
2.2 裂纹位移展开轮廓
对于复合材料界面分离状态,可以通过裂纹展开位移轮廓来描述。在只考虑界面发生分离时就认为材料开始形成裂纹,则复合材料的裂纹展开位移表达式为

对于平行排列的CNTs,在距镁基体裂纹端x处的裂纹展开位移轮廓定义为
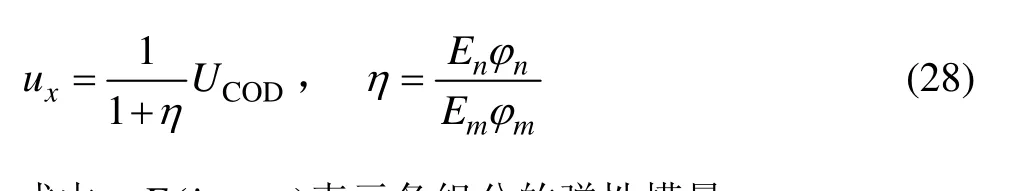
式中:Ei(i=n, m)表示各组分的弹性模量。
3 结果与分析
3.1 界面能量释放率随镁基复合材料参数的变化规律
图3所示为界面能量释放率随界面分离长度的变化。从图3可以看出,在界面分离长度较小(Ld<70 nm)时,界面能量释放率随界面分离长度的增加而保持一个较小的值不变,但是在界面分离长度(Ld>70 nm)后,能量释放率随界面分离长度的增加急剧的增加。同时,可以得到能量释放率是随界面厚度p的增加而增加的。这说明只有在界面分离长度较长时才对能量释放率有较大的影响,即体现了界面分离越长所需要的能量就越高。对于界面其越厚则能量释放率就越大,越容易在界面形成裂纹。
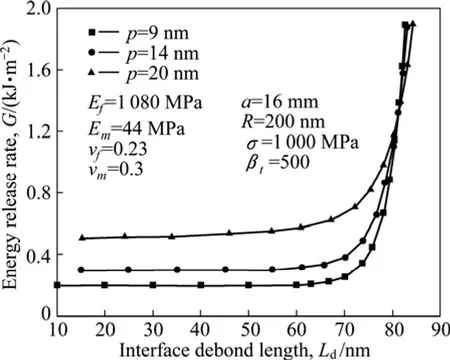
图3 能量释放率随界面分离长度的变化Fig.3 Variation of energy release rate with interface debonding length
图4所示为能量释放率随界面弹性模量的变化。图4表明在界面材料的弹性模量En较小(En<50 GPa)时,界面分离能量释放率随界面材料的弹性模量 En的增加而减小,而在界面材料的弹性模量 En较大(En>50 GPa)时,随着界面材料的弹性模量En的增加而增加。这说明界面材料参数的选择存在着最佳值(En=50 GPa)。此最佳值可以为界面材料的选择提供依据,因为裂纹通常是沿着产生最大能量释放率的方向扩展。同时,在界面材料弹性模量En较小时,界面厚度对能量释放率影响不大。在弹性模量(En>50 GPa)时,弹性模量的增加对能量释放率的影响越来越大。
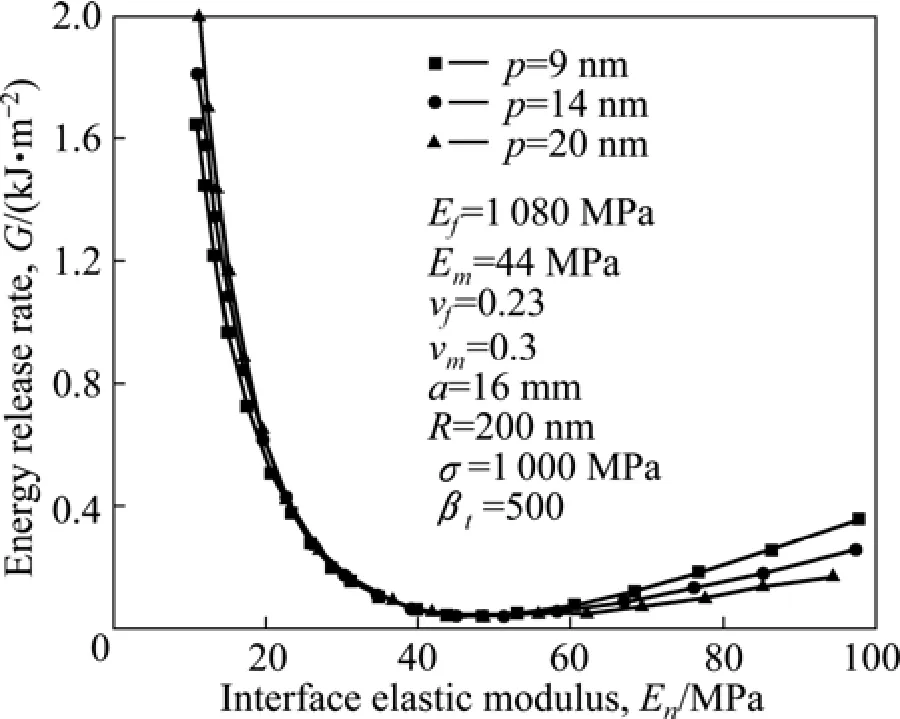
图4 能量释放率随界面弹性模量的变化Fig.4 Variation energy release rate elastic with interface modulus
图5所示为能量释放率CNTs长径比的变化。由图5可知:在碳纳米管长径比较小(βt<380)时,界面能量释放率随着碳纳米管长径比增加而急剧减小,但在碳纳米管长径比(βt>380)时,随着碳纳米管长径比的增加而保持一个较小的值不变。这说明:在一定范围内,镁基复合材料中增强体的长径比越小,越容易在界面处形成裂纹;增强体的长径比越大对镁基复合材料的增强效果越明显。在此条件下,界面厚度对能量释放率几乎没有影响。
图6所示为能量释放率随界面泊松比的变化。图6表明在界面材料泊松比 vn较小(vn<0.3)时,界面分离能量释放率随界面材料泊松比vn的增加而减小,而在界面材料泊松比 vn较大(vn>0.3)时,随着界面材料泊松比vn的增加而增加。这说明对于界面材料泊松比的选择也存在着最佳值(vn=0.3)。同时,在界面材料泊松比vn较小时,界面厚度对能量释放率影响不大。当泊松比较大(vn>0.3)时,随着泊松比vn的增加对能量释放率的影响越来越明显。
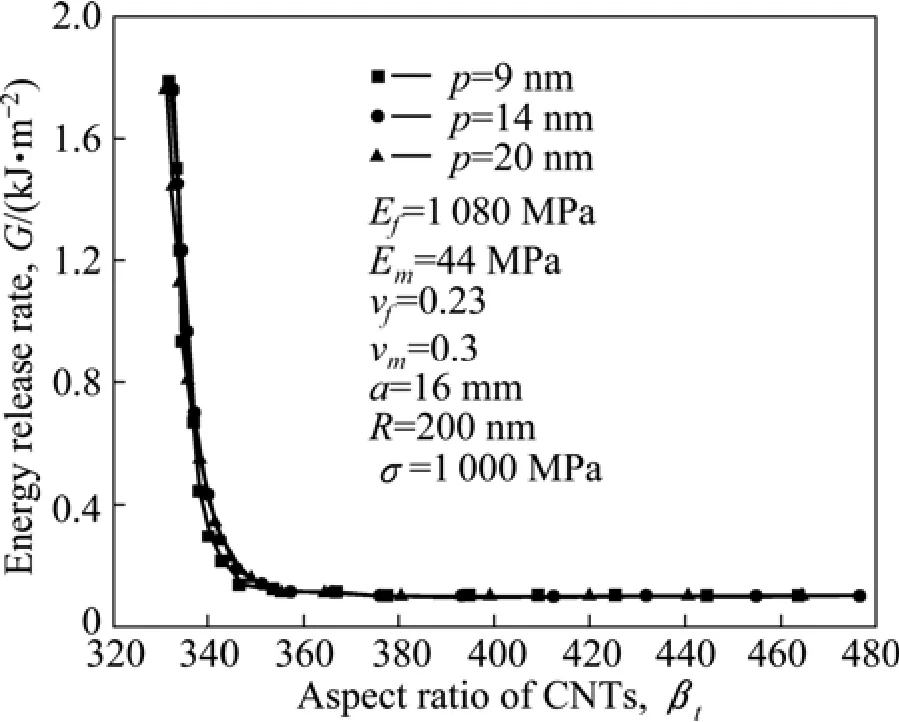
图5 能量释放率随CNTs长径比的变化Fig.5 Variation of energy release rate with CNTs aspect ratio
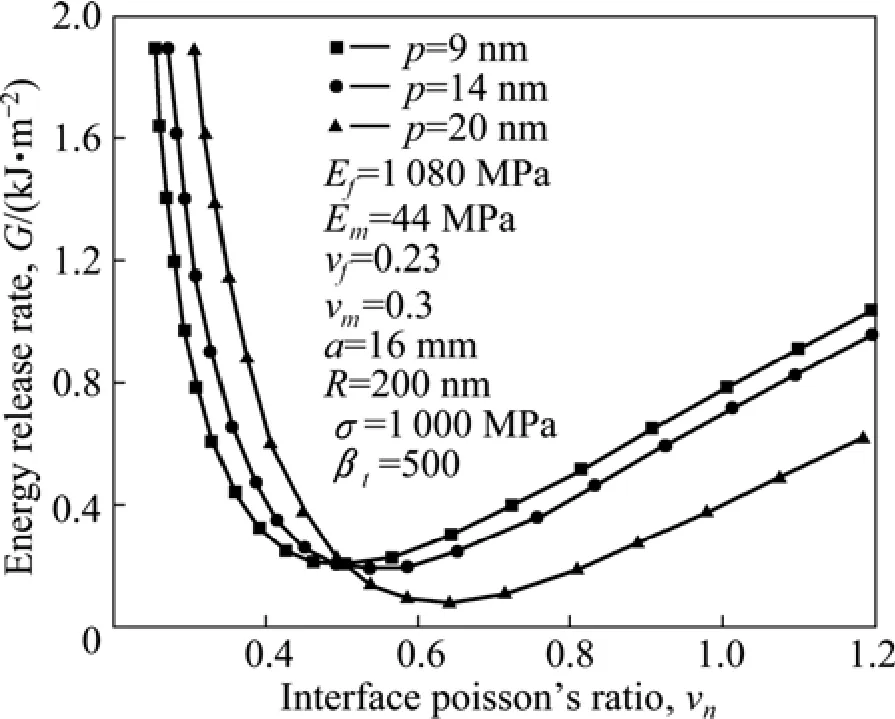
图6 能量释放率随界面泊松比的变化Fig.6 Variation of energy release rate with interface Poisson’s ratio
3.2 裂纹位移展开轮廓随镁基复合材料参数的变化规律
图7所示为裂纹位移展开轮廓随CNTs长径比的变化。从图7可以看出:在碳纳米管长径比较小(βt<150)时,镁基复合材料裂纹位移展开轮廓随着碳纳米管长径比的增加而急剧减小,但在碳纳米管长径比(βt>150)时,随碳纳米管长径比增加而保持一个较小的值不变。这也说明增强体的长径比较小时,更容易在纤维与界面间形成裂纹;在增强体长径比较长时,对镁基复合材料起到了很好的桥联作用。此条件下,分离界面的裂纹位移展开轮廓随界面厚度的增加而增加。
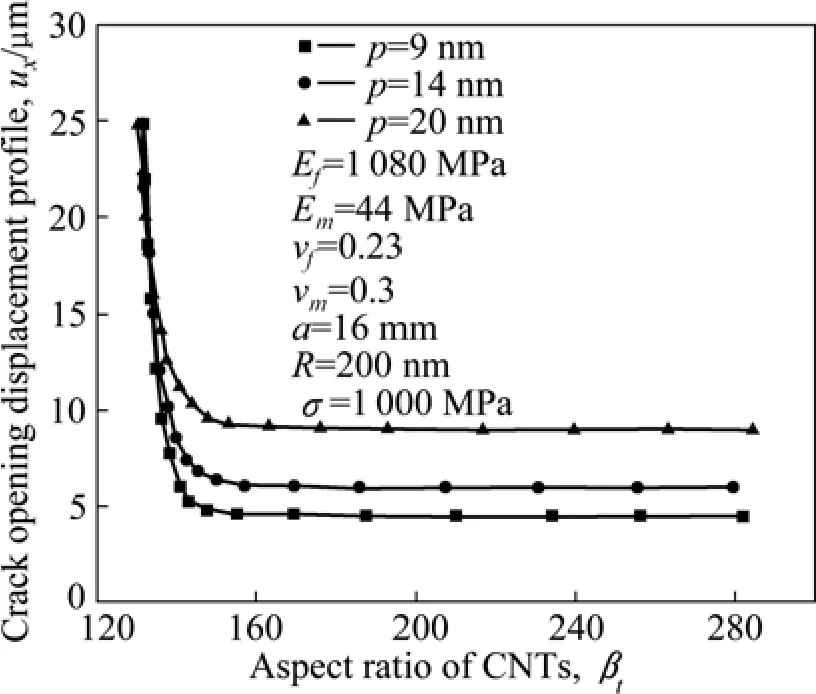
图7 裂纹位移展开轮廓随CNTs长径比的变化Fig.7 Variation of crack opening displacement profile with CNTs aspect ratio
图8表明在界面材料的弹性模量较小(En<60 GPa)时,界面材料弹性模量En的变化对镁基复合材料的裂纹位移展开轮廓影响较大,然而随着界面材料的弹性模量 En的继续增加裂纹位移展开轮廓越来越趋向于某一常数,这说明界面材料弹性模量对裂纹位移展开轮廓的影响是有限的。此条件下,分离界面的裂纹位移展开轮廓随界面厚度的增加而增加。
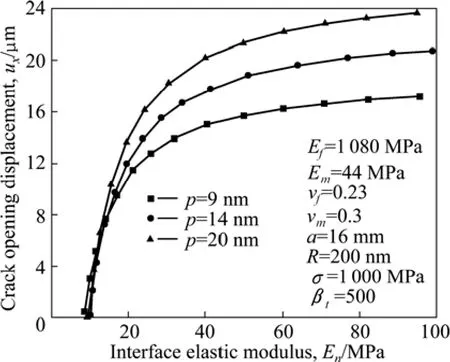
图8 裂纹位移展开轮廓随界面弹性模量的变化Fig.8 Variation of crack opening displacement profile with elastic modulus of interface
图9和10表明分离界面的裂纹位移展开轮廓是随着界面材料泊松比vn和分离长度Ld的增加而增加的;分离界面的裂纹位移展开轮廓也随界面厚度的增加而增加。说明界层材料泊松比vn、界面厚度和分离长度Ld越大越容易引发裂纹的扩展。
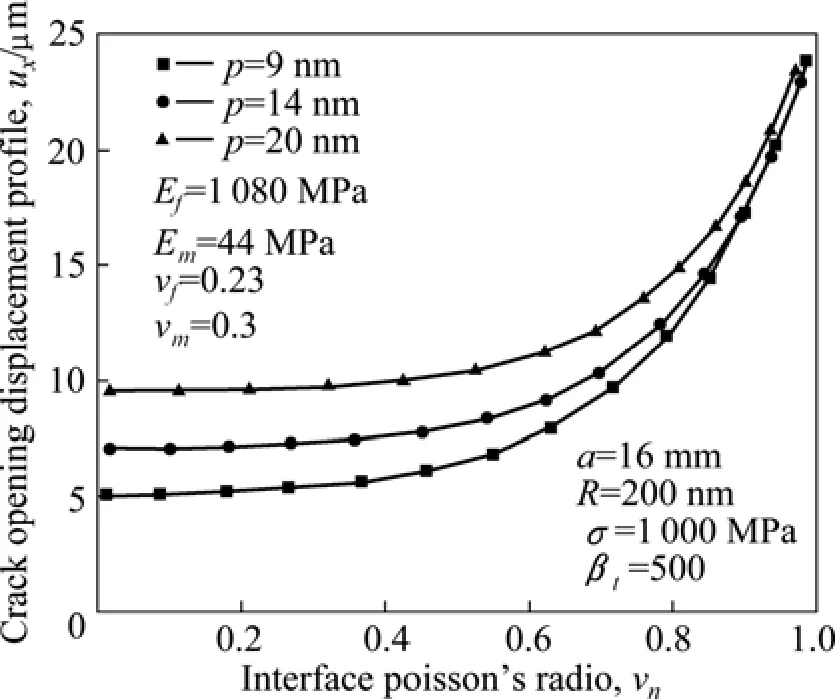
图9 裂纹位移展开轮廓随界面泊松比的变化Fig.9 Variation of crack opening displacement profile with Poisson’s ratio of interface

图10 裂纹位移展开轮廓随界面分离长度的变化Fig.10 Variation of crack opening displacement profile with debonding length of interface
4 结论
1) 考虑泊松效应和分离界面上摩擦应力的作用,建立了界面弹性应力传递摩擦拔出模型,得到界面分离能释放率和裂纹位移展开轮廓的表达式。
2) 界面分离长度和厚度越大,则镁基复合材料的界面分离能释放率就越大;碳纳米管长径比越小,则镁基复合材料的界面分离能释放率就越大。若能量释放率越大,界面越容易出现脱粘,越易于纤维拔出。对界面材料弹性模量和泊松比的选择存在着最佳值。
3) 界面分离长度、界面厚度、弹性模量和泊松比较大时,对镁基复合材料的裂纹位移展开轮廓影响较大;碳纳米管长径比较小时,对裂纹位移展开轮廓影响较大,此时容易在界面形成滑移和裂纹的产生与扩展。
REFERENCES
[1] 师昌绪, 李恒德, 王淀佐, 李依依, 左铁镛. 加速我国金属镁工业发展的建议[J]. 材料导报, 2001, 15(4): 5−6.SHI Chang-xu, LI Heng-de, WANG Dian-zuo, LI Yi-yi, ZOU Tie-yong. A proposal on accelerating development of metallic magnesium industry in china[J]. Materials Review, 2001, 15(4):5−6.
[2] 余 琨, 黎文献, 李松瑞. 变形镁合金材料的研究进展[J]. 轻合金加工技术, 2001, 29(7): 6−11.YU Kun, LI Wen-xian, LI Song-rui. The research and developments of wrought magnesium alloy[J]. Light alloy fabrication technology, 2001, 29(7): 6−11.
[3] JIA Zhi-jie, WANG Zheng-yuan, LIANG Ji. Production of short multi-wall carbon nanotubes[J]. Carbon, 1999, 37(5): 903−906.
[4] YOUNG H L, SCONG G K, DAVID T. Catalytic growth of single-wall carbon nanotubes [J]. Phys Rev Lett, 1997, 78:2393−2398.
[5] SALVETART J P, KUIK A J. Electronic and mechanical properties of carbon nanotubes [J]. Advanced Materials, 1999,22: 161−168.
[6] 张万平, 张俊乾, 吴 坚. 金属基复合材料纤维断裂脱落后的应力分析[J]. 重庆大学学报, 2004, 27(9): 119−123.ZHANG Wan-ping, ZHANG Jun-qian, WU Jian. Analysis for a broken and debonding fiber in ductile matrix composites[J].Journal of Chongqing University, 2004, 27(9): 119−123.
[7] HSUEH C H. Crack-wake interfacial debonding criteria for fiber-reinforced ceramic composites[J]. Acta Materialia, 1996,44(6): 2211−2216.
[8] OCHIAI S, HOJO M, INOUE T. Shear-lag simulation of the progress of interfacial debonding in unidirectional composites[J].Composites Science and Technology, 1999, 59(1): 77−88.
[9] CHIANG Y C. On fiber debonding and matrix cracking in fiber-reinforced ceramics[J]. Composites Science and Technology, 2001, 61(12): 1743−1754.
[10] RAUCHS G, WITHERS P J. Computational assessment of the influence of load ratio on fatigue crack growth in fibre-reinforced metal matrix composites [J]. International Journal of Fatigue, 2002, 24(12): 1205−1211.
[11] JIANG X Y, GAO Q. Stress-transfer analysis for fibre/matrix interfaces in short-fibre-reinforced composites[J]. Composites Science and Technology, 2001, 61(10): 1359−1366.
[12] LIU Peng-fei, TAO Wei-ming, GOU Yi-mu. Properties of frictional bridging in fiber pull-out for fiber-reinforced composites[J]. Journal of Zhejiang University Science, 2005, 6:8−16.
[13] 刘鹏飞. SiC纤维增强复合材料的界面分离准则[J]. 浙江大学学报: 工学版, 2006, 40(11): 1883−1888.LIU Peng-fei. Interface debonding criteria in SiC fiber-reinforced composites[J]. Journal of Zhejiang University:Engineering Science, 2006, 40(11): 1883−1888.
[14] LIU G, MOUSTIEZ A, LESAGE J, PANIER S. A numerical fracture analysis of a stationary semicircular interface crack during interfacial indentation test [J]. Surface & Coatings Technology, 2006, 201: 2086−2091.
[15] 米红林, 方如华. 金瓷修复体双材料界面断裂强度有限元分析[J]. 同济大学学报: 自然科学版, 2005, 33(1): 99−103.MI Hong-lin, FANG Ru-hua. Finite element analysis of bimaterial interfacial fracture intensity in porcelain-fused-tometal restoration [J]. Journal of Tongji University: Natural Science, 2005, 33(1): 99−103.
[16] 张 明. 双材料界面裂纹小范围屈服边界元分析[J]. 清华大学学报: 自然科学版, 1997, 37(10): 99−102.ZHANG Ming. Boundary element analysis of small-scale yielding of bimaterial interface crack [J]. Journal of Tsinghua University: Science and Technology, 1997, 37(10): 99−102.
Interface debonding properties of carbon nanotube-reinforced magnesium matrix composites
ZHU Jie1, LI Wei-xue1,2, DAI Jian-feng1,2, WANG Qing1,2
(1. Department of Physics, Lanzhou University of Technology, Lanzhou 730050, China;2. State Key Laboratory of Gansu Advanced Non-ferrous Metal Materials,Lanzhou University of Technology, Lanzhou 730050, China)
A theoretical model on the frictional pull-out properties of CNTs/Mg composite was presented to describe the interfacial elastic stress transfer, then the stress and strain of respective components of CNTs/Mg composite were derived.Considering the Poisson’s effect and friction stress at the debonded interface and based on the energy equilibrium and the interphase strain criterion in the interfacial debonding process, an expression for the energy release rate and the crack opening displacement profile was derived. The effects of the parameters on the fracture characteristics of CNTs/Mg composite were investigated by the relative energy release rate and crack opening displacement profile. The results show that the greater the interface debond length and interface thickness are, the better the relative energy release rate can be obtained. Larger interface debond length, interface thickness, interface elastic modulus and interface Poisson’s ratio have more influence on the crack opening displacement profile. The smaller the CNTs aspect ratio is, the better the relative energy release rate and the crack opening displacement profile can be obtained. The interface elastic modulus and interface Poisson’s ratio have optimum effects for the magnesium matrix composites.
carbon nanotube; magnesium matrix composites; interphase; energy release rate; crack opening displacement profile
TB 331
A
1004-0609(2011)11-2888-08
国家自然科学基金资助项目(50873047);甘肃省科技计划资助项目(1010RJZA045);兰州理工大学博士基金资助项目
2010-10-26;
2011-05-10
李维学,教授,博士;电话:0931-2975260;E-mail:lwx@lut.cn
(编辑 龙怀中)

