基于牵制控制的一类线性耦合复杂网络同步
吴雪飞,徐 晨
1)深圳大学信息工程学院,深圳518060;2)深圳职业技术学院计算机与软件工程学院,深圳518055
复杂网络存在于现实世界中,人们在生活和工作中随时接触各种各样的复杂网络[1-3],如因特网、生物神经网络、电力网、生态网及交通网等,复杂网络已成为人们日常生活中必不可少的一部分.同步现象是自然系统中一种典型的集体行为现象[4-6].早在17世纪,科学家就发现挂在同一横梁上的两个钟摆,无论起始高度是否一样,最终都能同步到同一振幅.根据结构决定功能的观点,在证实研究和网络建模的基础上探讨和预测网络系统的行为已成为复杂网络同前研究的热点.
复杂网络的同步研究有助于理解网络对复杂系统同步现象的影响,其中牵制控制核心思想是网络中小部分节点能够“引领”网络中其他节点,逐渐实现整个网络的同步,这种牵一发而动全局的思想已在众多复杂系统的同步研究中得到验证.例如,在生物群落中,蚁后蜂后具有整个蚁群蜂群的绝对统治;在社会系统中,群体意见的形成往往受到某个或某些关键领导者的影响等.因此,在复杂网络中如何对这些具有“领导能力”的节点实施有效控制,最终达到系统整体同步,是当今学者研究关注的课题[7-11].汪小帆等[9]提出可以将一个复杂动态网络牵制到其平衡点的一个有效方法.陈天平等[10]研究用一个单控制器来牵制一个复杂动态网络.同时,较之线性反馈控制,自适应牵制控制克服了预估反馈增益的问题,在处理网络同步方面独有见解,周进等[11]讨论用自适应控制的方法来牵制复杂网络.樊春霞等[12]利用节点输出变量构造同步控制器,针对输出耦合复杂网络的同步控制,提出一种自适应控制方法以实现复杂网络的同步.
本研究讨论一类线性耦合复杂网络系统的同步问题,使节点动力学性态条件f∈KΓ[13].采用与文献[14]相同的方法,通过对其部分节点牵制控制,最终实现该复杂网络所有节点均趋于同一状态.本研究还用自适应控制方法在实现网络同步的同时获得尽可能小的耦合强度,并通过数值模拟验证结论的正确性.
1 系统模型与相关知识
线性耦合常微分方程 (linearly coupled ordinary differential equations,LCODEs)是一类描述耦合连续时间系统的理论模型,并被广泛应用于时空复杂系统的研究中.在离散空间,它也常被用来描述耦合振子.通常LCODEs可用如下方程描述
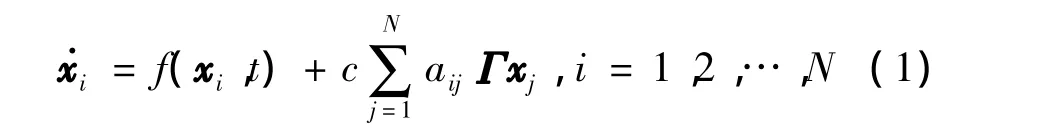
其中,N>1表示网络的节点数目;xi∈Rn表示第i个节点的状态变量;时间t∈[0,+∞);Γ表示一个内耦合矩阵;f:Rn×[0,+∞)表示连续的向量值函数;c>0表示耦合强度;耦合矩阵A=(aij)N×N用来描述网络的拓扑结构和权重,具体定义为:若节点i和节点j(i≠j)有边相连,则aij=1,否则aij=0.这里,矩阵A不一定对称,其对角线元素满足以下耗散耦合条件
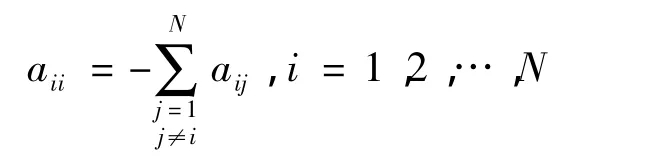
由式(1)描述的复杂网络系统同步可叙述为,若网络中所有节点的状态变量满足x1(t)=x2(t)==1,2,…,N,则称网络完全同步 (complete synchronization),其中s(t)表示非耦合系统的一个解,
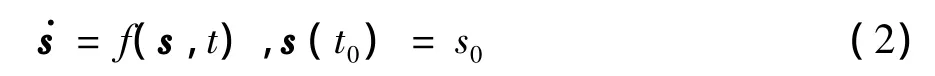
这里s(t)可以是一个平衡点,或是周期轨、拟周期轨及混沌轨道.定义向量x的范数为
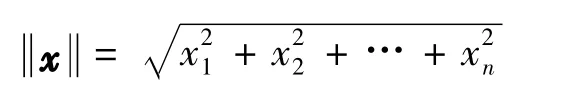
为方便讨论及证明文中主要结论,本研究引入以下概念和引理.
定义1[13]存在一个常数矩阵K满足条件
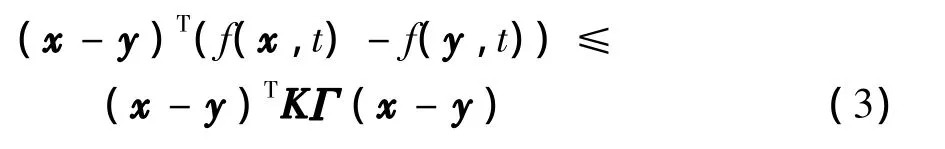
其中,∀ x,y∈Rn.
若f(x,t)满足上述条件,则称f(x,t)∈KΓ.可见,这个条件比较宽松.例如所有的线性和分段线性函数都满足这个条件;若 ∂fi/∂xj(i,j=1,2,…,n)有界,且Γ是正定的,则上述条件也成立.Lorenz系统、Chen系统、Lu系统、反馈神经网络及蔡式电路等都满足此条件.
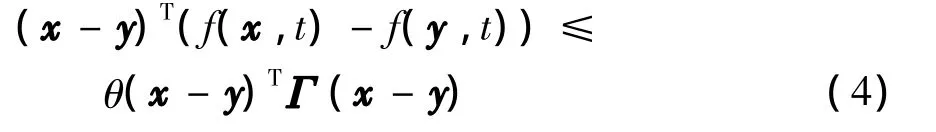
定义2[15]若存在常数M >0,μ >0,使得对任一初值xi(t0),其解xi满足
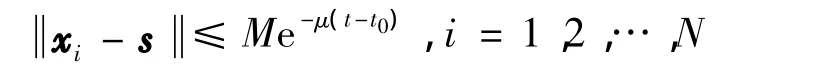
其中,s是系统 (2)的一个解,则称受控制的动态网络
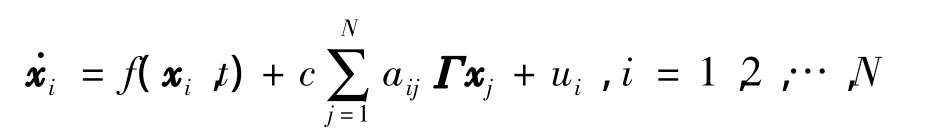
是全局指数稳定到轨道s上的.
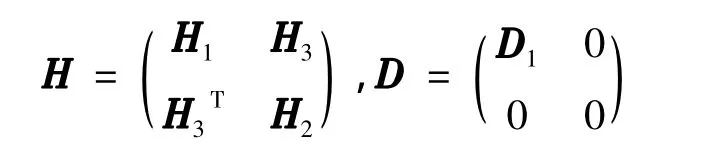
其中,H,D ∈ RN×N;H1,D1∈ Rr×r(r < N);D1=diag{d1,d2,…,dr}是一个正定对角矩阵,且H1T=H1;H2T=H2.若当di→+ ∞(1≤i≤r)时,λmax(H-D)存在,则
di→+∞(1≤i≤r),λmax(H-D)= λmax(H2).
引理1成立的一个局限在于控制增益di必须无限大,这在现实网络中是不可能的.为方便使用,一般引入一个松弛因子ε0来处理.即若λmax(H2)<0,则对某个ε0满足,必存在d >0,使得当di≥d时,λmax(H-D)≤λmax(H2)+ε0< 0.
引理1[14]假设
2 主要结论
为实现系统 (1)中各节点状态变量的同步,我们对该系统实施牵制控制.不失一般性,选择前l个节点进行牵制,即对系统(1)的前l个节点实施线性反馈控制,此时受控动态网络可描述为
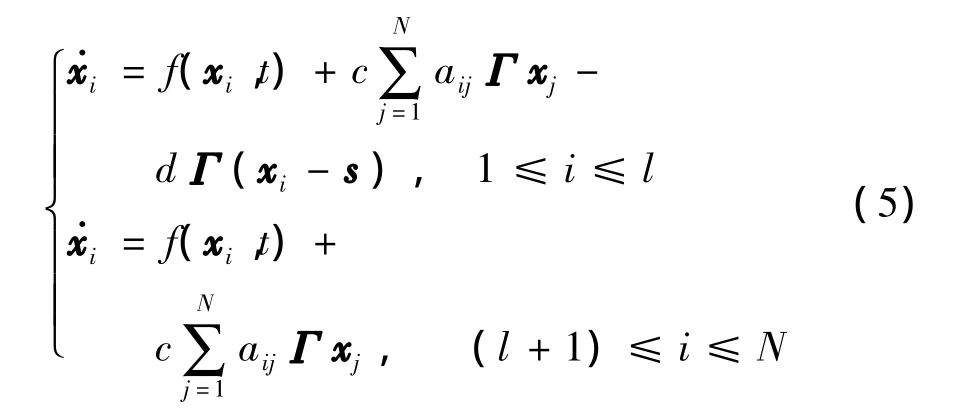
其中,d>0是反馈控制增益.
定义误差向量
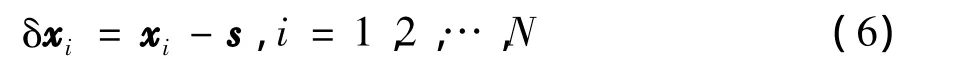
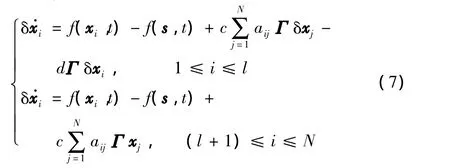
定理1 假设f∈KΓ,如果对某一ε0>0,存在一个自然数l∈[1,N-1]和一个反馈控制增益d,满足,那么受控动态网络(5)是全局指数同步到轨道s上的,其中λi是矩阵的Mi最大特征值,Mi是同时去除矩阵的前l行、l列所得的矩阵,^A是矩阵A的主对角元aii由取代后得到的矩阵.
【证】取Lyapnuov函数为
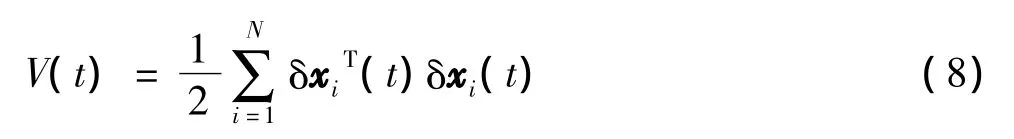
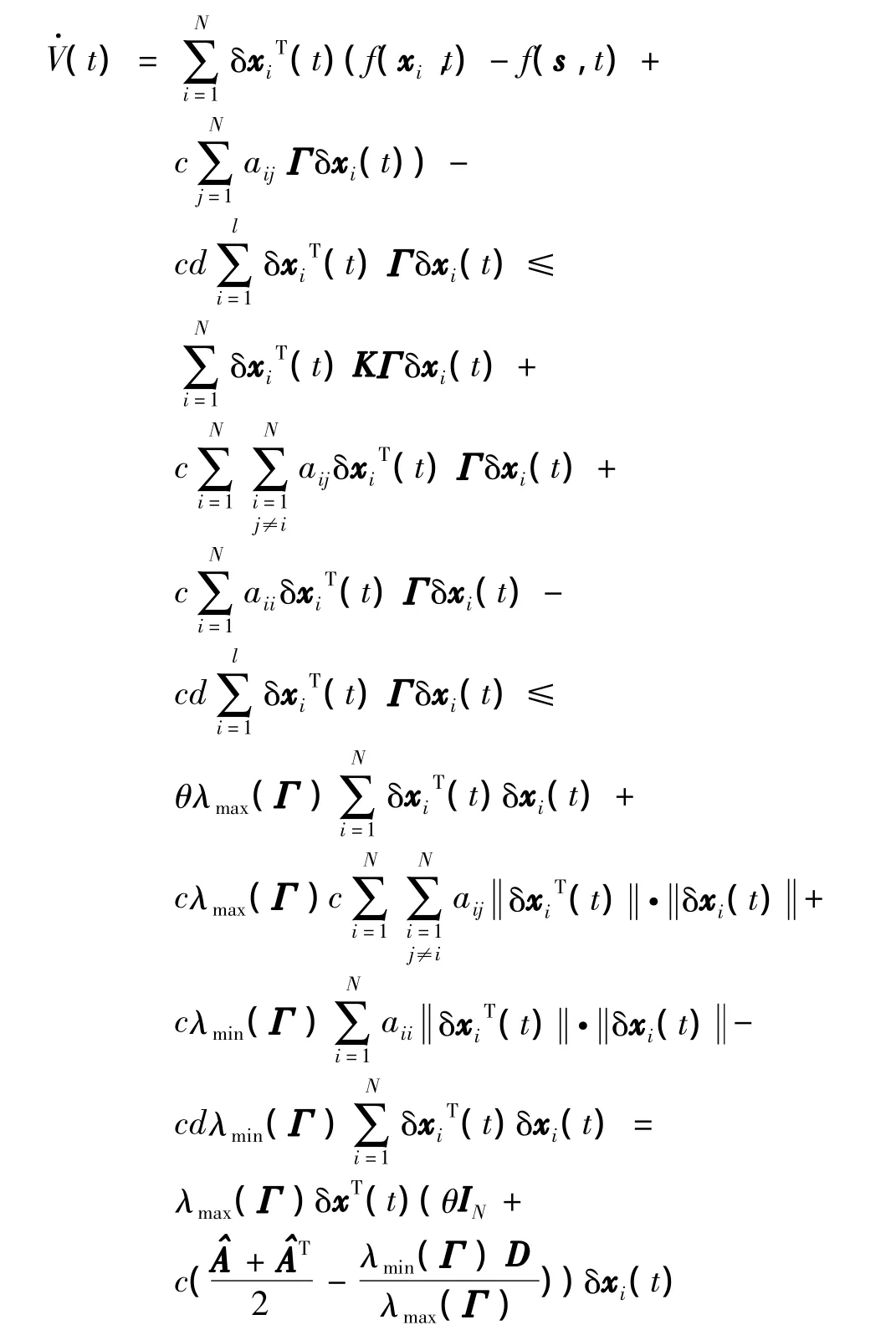
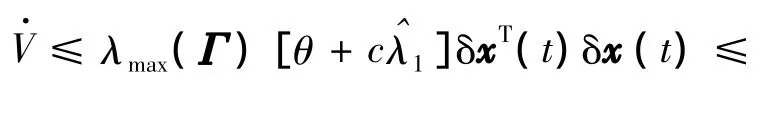
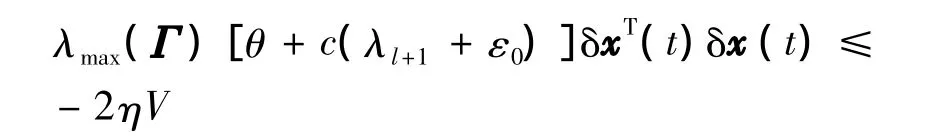
其中,η =-[θ+c(λl+1+ε0)].根据假设η >0,由比较定理得
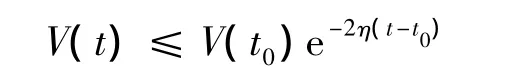
因此对 i=1,2,…,N
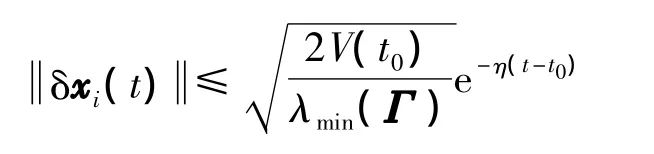
这样动态网络 (5)的各个状态变量在牵制控制下全局指数同步到了轨道s上,证毕.
定理1的条件中要求此复杂网络中耦合强度c较大,一般来说,耦合强度越大需要消耗的能量越多,为解决这一问题,常用的方法是对其实施自适应控制,即将耦合强度c看成是时间t的函数,使得在实施网络同步过程中自动调节耦合强度,以获取较为合理的耦合强度值,从而降低能量的消耗.自适应控制与常规反馈控制以及最优控制一样,都是一种基于数学物理模型的控制方法,不同的只是自适应控制所依据的关于模型的先验知识较少,需要在系统的运行和控制过程中不断发现和提取有关模型的信息,使模型逐渐完善.具体说,可依据对象的输入输出数据,不断辨识模型参数,不断改进和完善基于该模型综合出来的控制作用.从这个意义上讲,控制系统具有一定“随机应变”的适应能力.同时较线性反馈控制,自适应牵制控制克服了预估反馈增益的问题,使网络的同步能力得到极大提高,并能获得使网络同步的最小耦合强度,因此在处理网络同步方面有其独到之处.但自适应控制比常规反馈控制要复杂得多,成本也高,通常仅在常规反馈控制达不到期望的性能时,才考虑采用.
因此,动态网络(5)的误差系统和耦合强度c的自适应律为
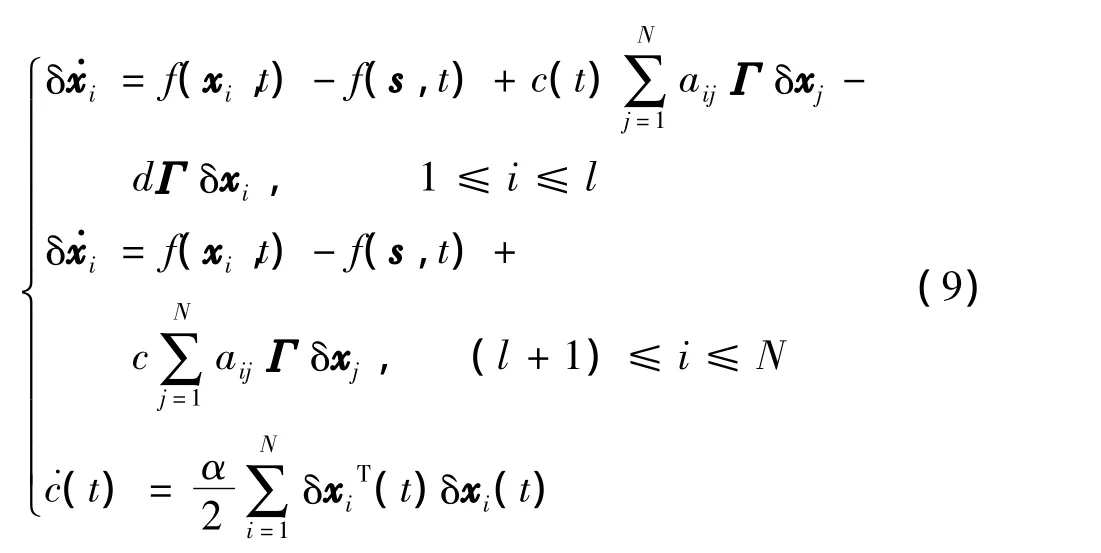
为方便起见,取 Γ =diag{γ1,γ2,…,γn},其中 γ1,γ2,…,γn为正常数.

取常数α>0,定义李雅普诺夫函数
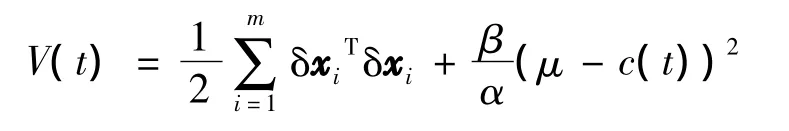
其中,常数β和μ将在后面确定.对其求导
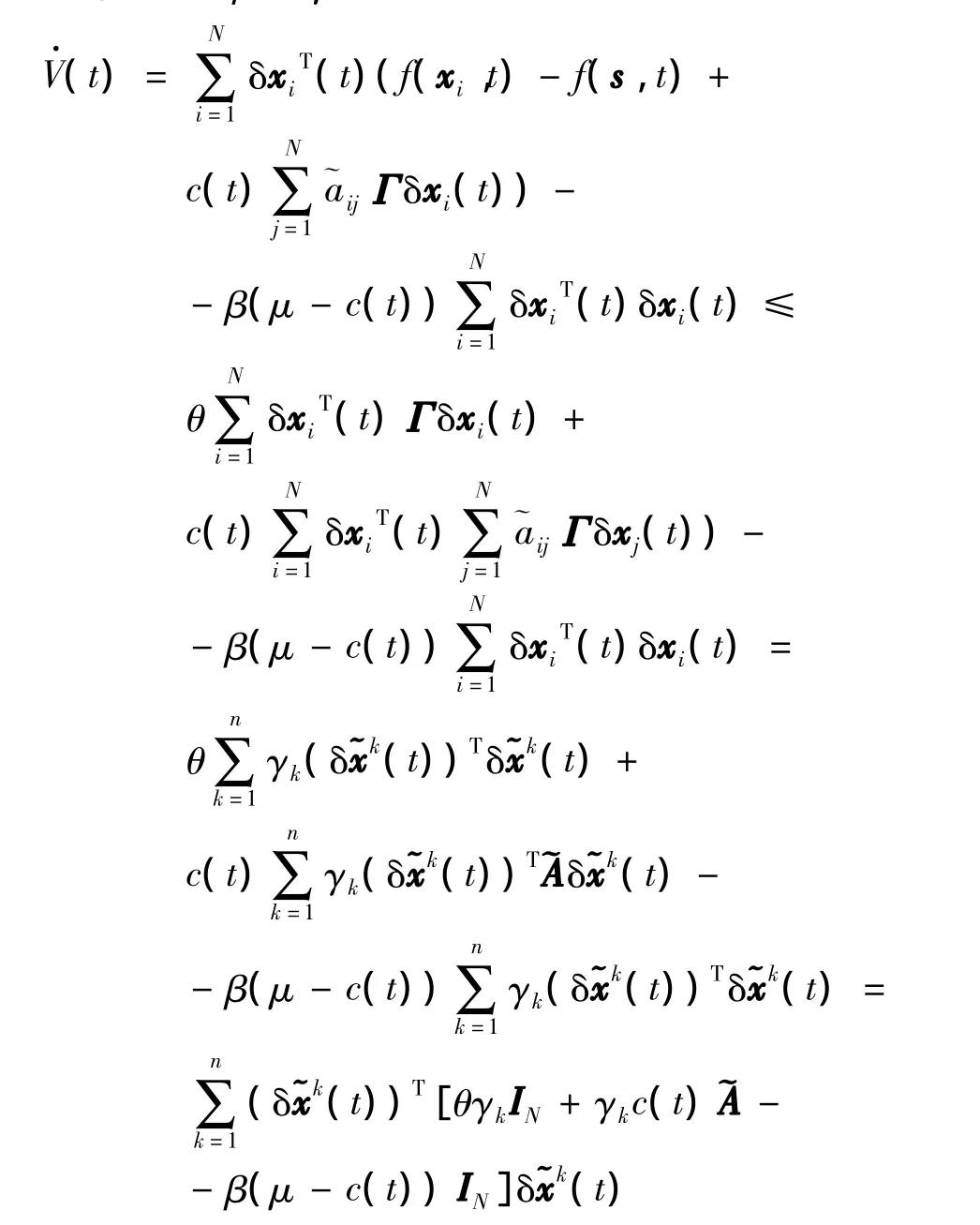
根据定理2的条件,有
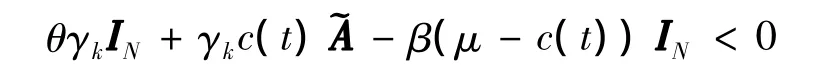
证毕.
3 数值模拟
本研究主要考虑小世界网络300个节点的情况,连接权重在[0,1]随机选择,并符合正态分布.采用上述同步条件研究具有相同动力学行为的300个节点复杂网络,其中非耦合节点的动力学系统用Lorenz系统反映,并在第一个节点实施牵制控制.Lorenz系统表达式为
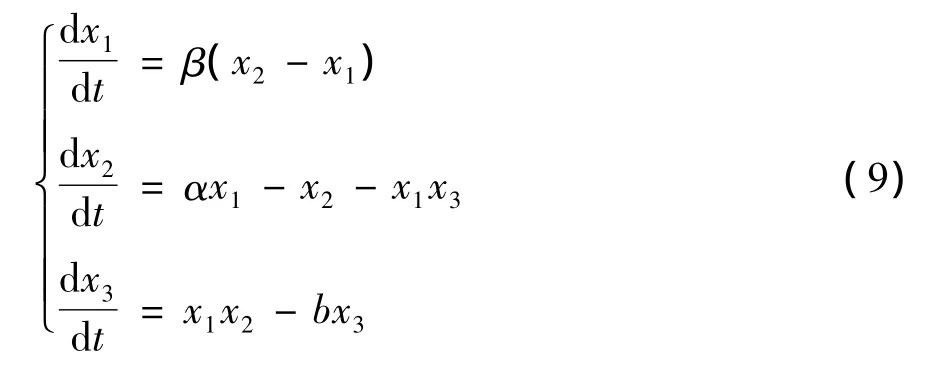
其中,β =10,α =28,b=8/3.
系统 (1)中,f(·)是混沌Lorenz振子,取i0使取控制增益 d=2,用来描述牵制过程的同步质量.
图1表示一般复杂耦合网络的常规牵制过程,选择 m=300,n=3,c=40,d=2.图2表示自适应方法E(t)和c(t)的变化曲线.
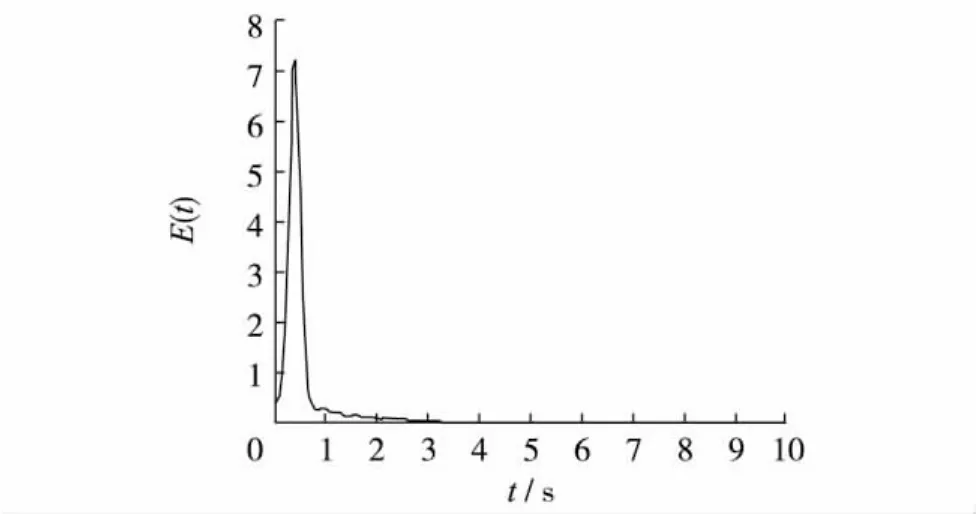
图1 300个节点的线性耦合网络的牵制同步过程Fig.1 The synchronization of a network with linear coupling of 300 nodes by pinning control
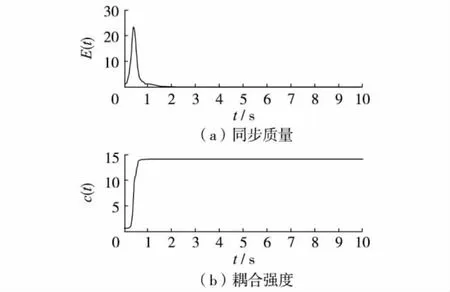
图2 300个节点的线性耦合网络自适应同步过程Fig.2 The synchronization of a network with linear coupling of 300 nodes by adaptive control
结 语
本研究讨论了一类复杂动态网络的同步问题,通过对其部分节点的牵制控制,实现所有节点均趋于同一状态,运用李雅普诺夫稳定性理论给出证明,得到了达到全局指数同步的充分条件.对该复杂网络的耦合强度实施自适应控制,达到实现复杂网络同步的同时,获得较小的耦合强度.数值模拟结果证实该理论结果正确.
[1] Barrat A,Weigt M.小世界网络的特性 [J].欧洲物理B,2000,13(3):547-560.(英文版)
[2] Strogatz S H.复杂网络探索 [J].自然,2001,410:268-276.(英文版)
[3] Watts D J,Strogatz S H.小世界网络的动态收敛 [J].自然,1998,393:440-442.(英文版)
[4] Pecora L M,Carroll T L.同步耦合系统的稳定性 [J].物理评论快报,1998,80(10):2109-2112.(英文版)
[5] Wu C W,Chua L O.线性耦合动力系统的序列同步[J].IEEE 系统汇刊I,1995,42(8):430-447.(英文版)
[6] ZHOU Jin,CHEN Tian-ping.一般复杂时滞动态网络的同步 [J].IEEE电路系统汇刊I,2006,53(3):733-744.(英文版)
[7] XIANG Lin-ying,LIU Zhong-xin,CHEN Zeng-qiang,等.以少量反馈控制器牵制多种时滞的权重复杂网络研究 [J].中国科学 F,2008,51(5):511-523.(英文版)
[8] ZHAN Meng,GAO Ji-hua,WU Ye,等.使用牵制控制的耦合系统的混沌同步 [J].物理评论E,2007,76(3):036203-1-036203-6.(英文版)
[9] LI Xiang,WANG Xiao-fan,CHEN Guan-rong.牵制一个复杂动态网络到其平衡态 [J].IEEE电路系统汇刊I,2004,51(10):2074-2087.(英文版)
[10] CHEN Tian-ping,LIU Xi-wei,LU Wen-lian.用单控制器牵制复杂网络 [J].IEEE电路系统汇刊I,2007,54(6):1317-1326.(英文版)
[11] ZHOU Jin,LU Jun-an,LU Jin-hu.一般复杂动态网络的自适应牵制同步 [J].自动化,2008,44(4):996-1003.(英文版)
[12] 樊春霞,蒋国平.输出耦合的复杂网络自适应牵制同步 [J].应用科学学报,2010,28(2):203-208.
[13] YU Wen-wu,CHEN Guan-rong,LU Jin-hu.复杂动态网络的牵制同步 [J].自动化,2009,45(2):429-435.(英文版)
[14] ZHAO Jun-chan,LU Jun-an,WU Xiao-qun.一般复杂动力网络的优化牵制控制 [J].中国科学:信息科学,2010,40(6):821-830.(英文版)
[15] LU Wen-lian,CHEN Tian-ping,CHEN Guan-rong.由微分方程描述的线性时滞耦合系统的同步分析 [J].物理 D,2006,221(2):118-134.(英文版)

