一道硕士研究生入学试题和三个例题的统一改进
刘玉记
(广东商学院数学与计算科学系,广州 510320)
一道硕士研究生入学试题和三个例题的统一改进
刘玉记
(广东商学院数学与计算科学系,广州 510320)
统一改进一道研究生入学考试《数学分析》试题和三道例题.
数学分析;研究生入学考试试题;改进结果
文献[3]有下面的三道例题:
例77 设f(x)在(-∞,+∞)二次可微,且对任意x∈(-∞,+∞),有
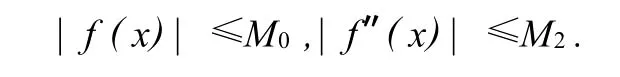
证明:对任意x∈(-∞,+∞),有|f′(x)|≤2M1M2.例78 设f(x)在(a,+∞)二次可微,且在(a,+∞)上分别有上确界M0,M1.证明:对任意x∈(a,+∞),有|f′(x)|≤4M1M2.
2006年,某著名大学研究生入学考试《数学分析》试题中选了下面的题目:
题目1 设函数f(x)在[0,+∞)有二阶连续导数,且对任意x∈[0,+∞),有|f(x)|≤A,|f″(x)|≤B.证明:对任意x∈(0,+∞),有|f′(x)|≤2
证对任意c∈(0,+∞),作区间[x,x+k],使得c∈[x,x+k]⊂(0,+∞),而且c-x充分地小,其中k=2.由于存在ξ1,ξ2∈[x,x+k],使得
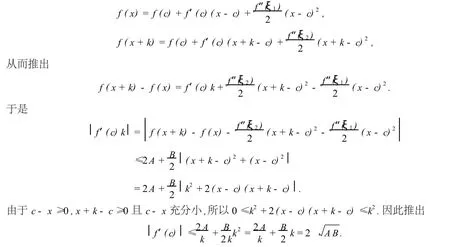
定理1 设函数f(x)在(-∞,+∞)有二阶导数,且对任意x∈(-∞,+∞),有|f(x)|≤A, |f″(x)|≤B.证明:对任意x∈(-∞,+∞),有|f′(x)|≤

注2 例题76,77,78中的结果也有相应的改进.
注3 本文结果可以推广到高阶导数情形.限于篇幅,略.从注1,我们可以猜想:设函数f(x)在(-∞,+∞)有二阶导数,且对任意x∈(-∞,+∞),有|f(x)|≤A,|f″(x)|≤B,则如下的结论是正确的:对任意x∈(-∞,+∞),有|f′(x)|≤,但是作者未能证明这一结论.
[1] 陈纪修,淤崇华,金路.数学分析(上册)[M].北京:高等教育出版社,1999.
[2] 陈纪修,等.数学分析习题全解指南(上册)[M].北京:高等教育出版社,2005.
[3] 胡雁军,李育生,邓聚成.数学分析中的证题方法与难题选解[M].郑州:河南大学出版社,1987.
O17-42
C
1672-1454(2011)03-0209-02
2008-01-14
——庆祝湖南农业大学草业科学系建系20 周年

