地震走时层析成像反演在速度模型中的应用

陈爱琼 (地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

周 霞 (长江大学地球科学学院，湖北 荆州 434023)

朱海东，杜浩坤 (地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

地震走时层析成像反演在速度模型中的应用

陈爱琼 (地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

周 霞 (长江大学地球科学学院，湖北 荆州 434023)

朱海东，杜浩坤 (地球探测与信息技术教育部重点实验室(成都理工大学)，四川 成都 610059)

基于在均匀介质中的波射线传播理论，应用直射线追踪方法进行了射线走时正演计算，并选用了SIRT算法根据不同的点源和不同的检波点的走时观测值进行快速反演成像，并对不同的反演结果进行比较，获得了在不同走时观测值所反演得到速度异常区域的位置。

地震走时层析成像；反演；直射线追踪；SIRT算法

CT(Computerized Tomography，计算机层析成像)是一种根据投影数据反演物体内部图像的方法。在1917年 奥地利数学家J.Radon 提出层析成像理论后, A.M.Cormack、Langan、Bishop、Chiu等的研究进一步发展了走时层析成像技术[1]。由于层析成像探测技术具有分辨率高、探测范围广、成像结果直观等特点,近几十年来, 被广泛应用于工程探查、地质构造探测、资源勘探开发、地震探测以及工程质量检测等领域。层析成像方法按投影数据类型可分为走时层析、振幅层析和波形层析[2]。下面，笔者针对走时层析成像技术，研究在均匀介质中确定速度异常区域位置与观测点所接收走时观测值的关系。

1 直射线正演计算

层析成像正演算法可以分为2类[3]:一类是基于射线理论的射线追踪方法，另一类是对波场进行数值模拟方法。目前, 在工程中应用最广、最为成熟的是基于射线理论的层析成像方法。

1.1测量原理

以跨孔测量为例，在待测区的左侧布置点源，右侧布置检波点。在点源激发信号后，在右侧检波点接收信号，射线会覆盖整个测量区域。

走时层析成像又包括速度层析和衰减层析。以速度层析为例, 计算公式为:

AX=B

(1)

式中，A为系数矩阵；X为慢度矩阵(向量)(速度的倒数)；B为走时观测值。将式(1)离散后，得到如下所示结果：

(2)

式中，aij第i条射线在第j个单元内的路径长度；xj=1/vj是第j个网格单元内的慢度值(速度值的倒数)；bi是第i条射线的走时实测值。

地震走时层析成像正演计算是为了准确求得射线走时观测值B。在式(1)中, 由于X作为已知量输入, 因此射线走时观测值计算准确与否就取决于A矩阵的构造方法是否适合。A矩阵的计算包括直射线CT法和弯曲射线CT法。直射线法假设其射线路径是固定的，用其进行正演计算，速度快，而且均匀介质具有各向同性性质。在均匀介质中，波射线是直线，基于该特点，笔者采用直射线CT法进行正演计算。

1.2直射线法

直射线法以波在均匀介质中传播的路径是直线传播为理论基础。根据惠更斯-菲涅尔原理[4]，在弹性介质中，已知t时刻的同一波前面上的各点，可以把这些点看做从该点时刻产生子波的新的点震源，经过任何一个Δt时刻后，这些子波的包络面就是波t+Δt时刻到达的新的波前面。其具体追踪方法如下：由一个源点出发,计算从源点到其相邻所有网格点的走时和射线长度(在源点没有经过的网格其走时和射线长度都赋值为0),然后把除源点之外的所有网格点相继当作次级源 , 再计算从各个次级源点到其相邻网格点的走时和射线长度(在源点没有经过的网格其走时和射线长度都赋值为0)，将每次计算出来走时加上从波源到次级源走时, 作为波源点到该网格点的走时。这样依次进行追踪比较, 即可得出较为准确的射线路径。

2 联合迭代重建法(SIRT)

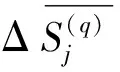
对每个象元的图像向量作修改，并留作下一轮迭代使用[7]。

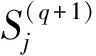
(3)

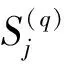
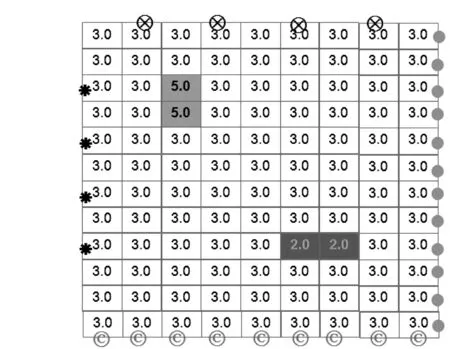
图1 速度模型

SIRT算法虽然占用内存较大，但具有较高的成像精度,并能明显克服个别数据误差较大所造成的结果失真和由于射线分布不均所造成的误差集中，而且收敛性较好,方程组无论是超定还是欠定都能适用,是走时层析成像常用的方法之一[2,7-8]。

3 数值模拟

数值模拟选择了如图1所示模型进行速度层析成像反演。正演模型为一个单元数为9×12，单元边长为3.0m×5.0m的速度传播区域，即横向和纵向步长分别是5.0m和3.0m，其中存在一个6m×5m的长方形高速异常区和一个3m×10m长方形低速异常区。每边设置4个点源，在其他3边检波点接收；上下2边的点源位置如上边圈叉图标所示；直立2边的点源如左边星状图标所示；上下2边的检波点位置如下边的圆圈所示；左右2边的检波点位置如右边的圆点所示。在此次的模拟试验中，将每一条射线离散为1个向量，每一个向量由108个元素组成，总共有144条射线，即可将成像区域划分为144×108个网格。模型背景速度为3000m/s，异常区域速度分别为5000m/s和2000m/s，迭代收敛精度值e等于0.1× 10-6。其反演结果如图2所示。

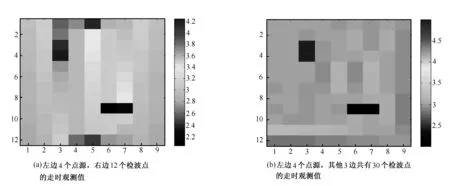
图2 反演结果

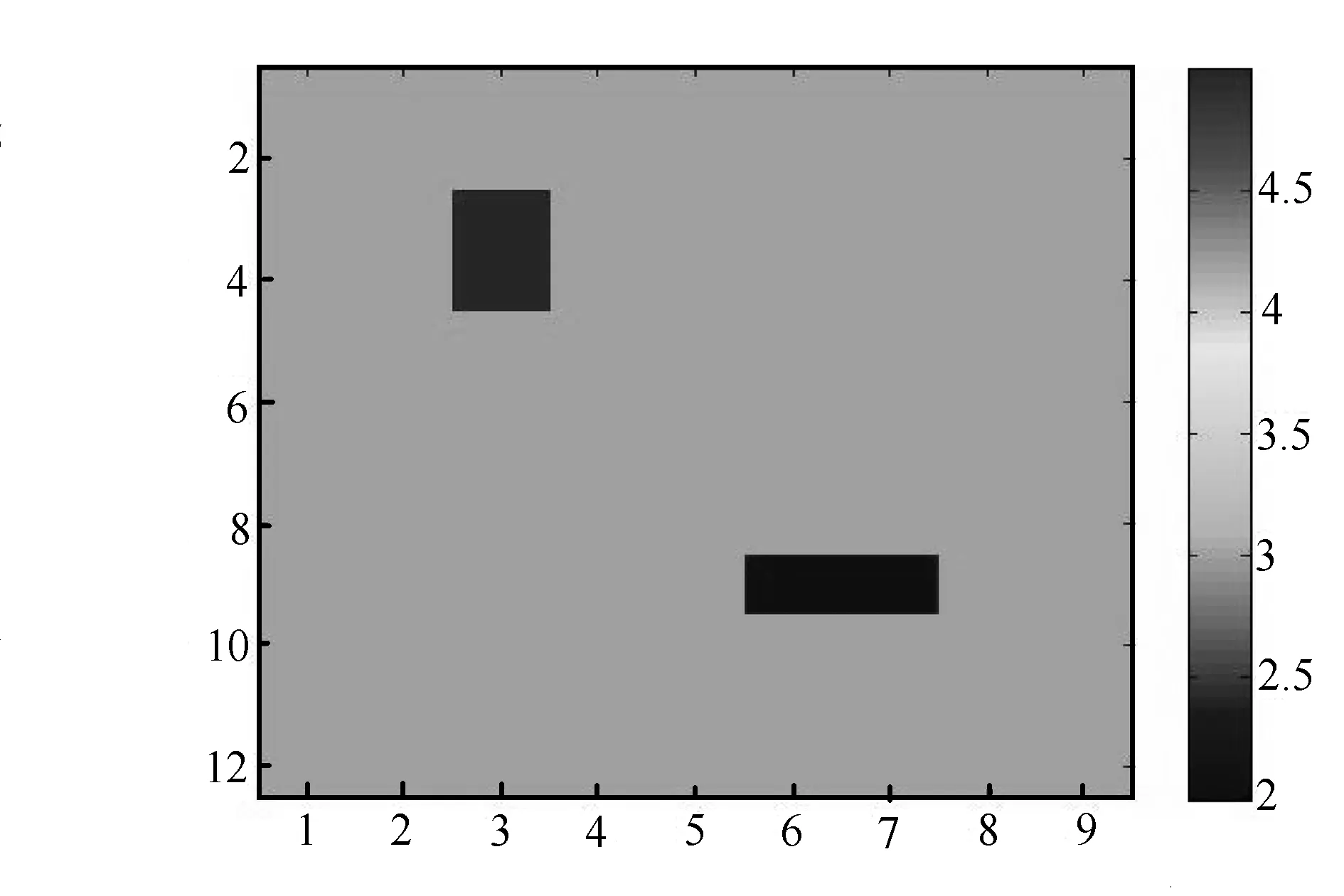
图3 所有点源激发，检波点接收的走时观测值反演结果

图2(a)是利用左边4个点源，右边12个检波点的走时观测值，用其进行反演，所得的成像图中能够反映高速异常区和低速异常区，但其结果存在多解性，而且高速异常值低于目的区的高速异常值，低速异常值高于目的区的低速异常值。图2(b)是利用左边4个点源，其他3边共有30个检波点的走时观测值进行反演，所得的成像图中能够反映高速异常区和低速异常区的位置，但其所得的背景值高于模型的背景速度值。故单边激发，3边接收反演结果精度要高于单边激发，单边接收反演精度。

图3是将16个点源激发后，168个检波点接收的走时观测值联立后的反演结果，在图中能确定高速异常区和低速异常区，其值大小为目的值的大小，结果中的背景值完全接近模型中的背景值，这说明反演效果已经达到最佳。

[1]刘国华, 王振宇, 孙坚.弹性波层析成像及其在土木工程中的应用[J].土木工程学报, 2003, 36( 5) : 76-81.

[2] 毛伟伟，于素萍.走时层析成像正反演方法研究[J].西安邮电学院学报，2010,15(1)：123-126.

[3] 和锐，杨建思, 张翼.地震层析成像方法综述[J].CT 理论与应用研究 , 2007, 16( 1) : 35-48.

[4]朱广生，陈传仁，桂志先.勘探地震学教程[M].武汉：武汉大学出版社，2005:86-87.

[5] 宋林平.平方慢度射线追踪与非线性地震走时层析反演[J].成都理工学院学报，1994,21(1)：107-113.

[6] 刘盛东, 李承华.地震走时层析成像算法与比较[J].中国矿业大学学报, 2000, 29(2) : 211-214.

[7] 常旭，刘伊克.地震正反演与成像[M].北京:华文出版社,2001:26-34, 85-95.

[8] 周建宇.井间地震研究与应用[D].兰州:中国科学院兰州地质研究所,2002.

[9] 刘良琼，刘江平，张英德.井间地震射线走时层析成像数值模拟[J].工程地球物理学报，2004,1(5)：441-446.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.06.013

P631.4

A

1673-1409(2011)06-0041-03

2011-03-28

陈爱琼，女，硕士生，现主要从事地震资料解释和储层预测方面的研究工作。