基于风能转换系统的T-S模糊建模与控制
孟 涛,沈艳霞,纪志成
(江南大学,江苏无锡214122)
0 引 言
风能是一种清洁、资源丰富、不产生温室气体的自然可再生能,在当前矿石能源面临枯竭、环境日益恶化的情况下,无论从经济上或是技术上都是一项可以首选的替代能源[1]。而风力发电作为一种新型的可再生能源,是世界范围内增长最快的一种能源形式,具有环境友好、技术成熟、全球可行的特点,在世界各地正得到越来越广泛的应用[2]。
风能转换系统的控制技术与系统的整体性能密切相关。文献[3]根据风能转换系统在特定工况点附近的线性化模型设计了线性二次型(Linear Quadratic,简称LQ)最优控制器,当系统在特定工况点小范围内工作时,线性二次型控制器的控制系能较好。但风能转换系统不仅具有很强的非线性,而且其工作点随风速不断变化。因此,针对某一工况点所设计的控制器在风速大幅度变化时难以达到风能转换系统的控制系能指标。不同于局部线性化方法借助于泰勒级数展开实现动态特性的线性近似,文献[4]采用反馈线性化原理设计了风力发电控制系统,并取得了良好的控制效果。但反馈线性化方法依赖于系统精确的非线性模型,对建模误差敏感,且不能处理动态系统的未知变化。本文受文献[5]的启发,建立了风能转换系统的T-S模糊模型。该模型不仅考虑到了整个风能转换系统的非线性,而且降低了对原有系统模型的要求。
T-S模糊模型[6]最初由Takagi和Sugeno于1985年提出,主要适用于非线性复杂系统的模糊动态建模。由于采用T-S模糊模型设计出的控制系统仍然可以利用线性系统的控制方法进行控制,因此T-S模糊控制系统的分析与设计以及如何能够将其与线性控制方法进行有效的结合已经是当前的研究热点。另外,T-S模糊模型不仅克服了用语言和规则描述模糊模型的缺点,而且解决了系统的非线性问题。目前,该方法也引起了风力发电技术研究者的广泛关注[5,7]。
本文首先给出了风能转换系统的非线性模型,其次基于T-S模糊模型良好的局部线性的特点将风能转换系统的非线性模型等价成T-S模糊模型,然后在每个线性的局部模型中分别设计线性控制器,并利用隶属度函数构成整个全局模型控制器。最后给出仿真分析,以验证基于风能转换系统的T-S模糊控制的有效性。
1 双馈风能转换系统建模
双馈风能转换系统主要由风轮机、传动系统、双馈发电机、交直交变换器和电网组成。风能由风轮机捕获并被转换为风轮机的机械能,风轮机通过传动系统带动双馈发电机转子旋转将机械能转换为电能,由交直交变换器将其转换为符合要求的交流电输送到电网。双馈风能转换系统的基本结构如图1所示。

图1 双馈风能转换系统基本结构
1.1 风轮机模型
风轮机由叶片和轮毂组成,是将风能转换为机械能的重要部件,直接决定着风能转换效率。
根据空气动力学原理,风轮机产生的机械功率[8]:

式中:ρ为空气密度;v(t)为风速,随时间变化;Rt为风轮半径;Cp[λ(t),β(t)]为风能转换系数,是λ(t)和β(t)的函数。风轮叶片的叶尖线速度与风速之比称为叶尖速比λ(t),即(t)为风轮旋转的机械角速度。
风轮机产生的风力矩:

式中:CΓ[λ(t),β(t)]为转矩系数,CΓ[λ(t),β(t)]
风能转换系统工作在额定风速以下时,通常将桨叶节距角β(t)置于0°附近而不进行调节控制,可将其视为常值,此时CΓ[λ(t),β(t)]=CΓ[λ(t)]。如果已知叶尖速比λ(t),则可以得出转矩系数时CΓ[λ(t),β(t)],可用一维查表法得到,也可以通过计算关于λ(t)的多项式得到,在这里取CΓ[λ(t)]=a0+a1λ(t)+a2λ2(t)[4],并将其代入式(2)得:

式中:a0=0.125 3,a1=-0.004 7,a2=-0.000 5。
1.2 传动系统模型
双馈风能转换系统的传动系统主要由低速轴、变速齿轮箱、高速轴组成,低速轴连接风轮,高速轴连接发电机转子,低速轴到高速轴由变速齿轮箱连接,风轮的机械能经过传动系统传递到双馈发电机转子。忽略粘性摩擦,刚性传动系统动力学方程[9]为:

式中:ωh为发电机转子转速,ωh(t)=ioωl(t);io为齿轮传动变速比;η为齿轮传动效率;ΓG(t)为发电机电磁转矩;Jh为传动系统高速轴端的总转动惯量;Jl为传动系统低速轴端的总转动惯量,并且JhJ1为齿轮高速端转动惯量,J2为齿轮低速端转动惯量,Jg为发电机转子的转动惯量,Jwt为风轮机转轴的转动惯量。
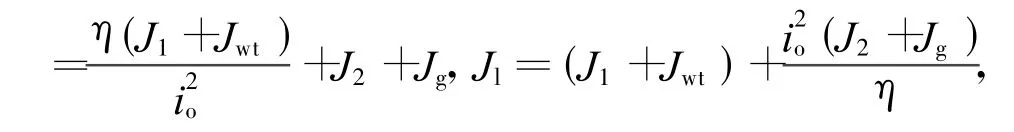
将ωh(t)=ioωl(t)代入,可得叶尖速比与发电机转子转速的关系式:

1.3 双馈感应发电机(DFIG)的数学模型
双馈感应发电机定转子三相绕组对称,并均匀分布在电机圆周内,磁路、电路对称分布。为了分析方便,现作如下假定:
(1)只考虑磁链、电压、电流的基波分量,忽略谐波分量;
(2)各绕组自感和互感都是线性的;
(3)忽略磁路饱和、磁滞、涡流损耗和铁耗;
(4)不考虑温度变化对双馈感应发电机参数的影响。
则双馈感应发电机在d-q同步旋转坐标系下数学模型[4]可由以下方程构成。
磁链方程:

电压方程:

电磁转矩方程:
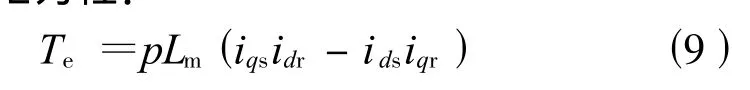
运动方程为:

式中:ids、iqs分别为定子d、q轴的电流;idr、iqr分别为转子d、q轴的电流;Ls为定子自感;Lr为转子自感;Lm为定转子之间的互感;ψds、ψqs分别为定子d、q轴磁链;ψdr、ψqr分别为转子d、q轴磁链;uds、uqs分别为定子d、q轴电压;udr、uqr分别为转子d、q轴的电压;ω1为定子同步角速度;ωr为转子电角速度;ω2为转差角速度,ω2=ω1-ωr,即d-q同步旋转坐标系相对转子的角速度;J为转动惯量;p为电机极对数;Te、Tm分别为电磁转矩和机械转矩。
2 风能转换系统的T-S模糊建模
2.1 风能转换系统的T-S建模
为了便于T-S建模,考虑到上述风能转换系统的建模过程,给出以下假设[4]:
(1)风速采用Van der Hoven风速模型;
(2)风能转换系数曲线已知,忽略结构力度;
(3)发电机是理想的,并且参数恒定;
(4)在整个风速范围内发电机的效率恒定;则风能转换系统的状态方程可以表示为:
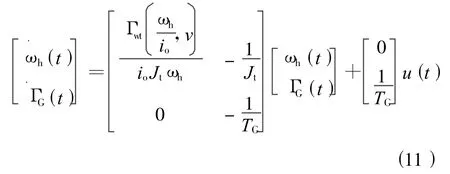
式中:Jt为高速轴端的转动惯量,值为
令:x(t)=[ωh(t)ΓG(t)]T,则式(11)可简记:


根据式(11),定义前提变量:z1(t)=ωh(t),z2(t)=ΓG(t),则式(8)中的系统矩阵A[x(t)]可写成新形式A[z1(t),z2(t)]。取ωh1≤min[ωh
(t)],ωhm≥max[ωh(t)];ΓG1≤min[ΓG(t)],ΓGn≥
max[ΓG(t)]。其中,ωh1和ωhm分别是转速的最小值和最大值,ΓG1和ΓGn为发电机电磁转矩的最小值和最大值。分别在区间[ωh1,ωhm]、[ΓG1,ΓGn]上再取m-2个点和n-2个点,则形成两个序列:
Z1=(ωh1,ωh2,…,ωhp,…,ωhm)
Z2=(ΓG1,ΓG2,…,ΓGq,…,ΓGn)
p=1,2,…,m;q=1,2,…,n
将序列Z1、Z2中的元素彼此匹配,并代替式(12)中A[z1(t),z2(t)]中的z1(t)、z2(t),即可得到一系列常数矩阵Apq,p=1,2,…,m;q=1,2,…,n。
T-S模糊模型的模糊规则定义如下:
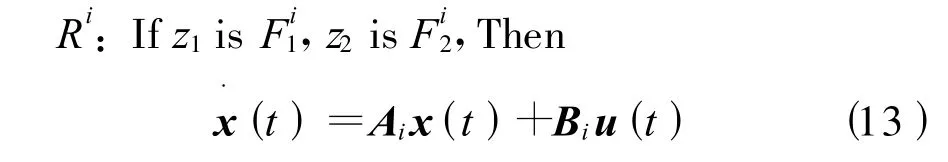
其中,Ri为第i条模糊规则,规则数r=m×n,i=1,2,…,r;i=m×(p-1)+q,i为p、q的函数,故定义i=i(p,q)。所以Ai=Ai(p,q)=Apq,可得到风能转换系统的T-S模糊模型的全局状态方程如下:


图2 隶属度函数结构图
2.2 风能转换系统的T-S模糊模型的仿真研究
为了验证本文提出的风能转换系统T-S模糊模型的有效性,首先在Matlab/Simulink环境下搭建风能转换系统T-S模糊仿真模型。因为在额定风速以下风能转换系统是利用转矩进行控制的,而电磁转矩的时间常数要远远小于传动系统的时间常量,因此在仿真模型中可以将电磁子系统等效为一阶惯性环节,其中仿真参数[10]如表1所示。

表1 仿真参数
为了仿真的简便,取m=2,n=2,则r=4。根据仿真参数取,ωh1=0,ωh2=400 rad/s,ΓG1=0,ΓG2=80 N·m。
则隶属度函数具体表示如下:

仿真波形如图3、图4所示,其中图3为在理想风速时传统风能转换系统和基于T-S模糊建立的风能转换系统的输出转矩曲线;图4为在随机风速时两种不同模型的输出转矩曲线。

图3 理想风速时的输出转矩曲线

图4 随机风速时的输出转矩曲线
由图3、图4分析可知:在风速为理想风速和随机风速两种不同工况下,在误差允许的范围内,基于T-S模糊建立的风能转换系统都可以与传统的风能转换系统模型保持很好的一致性,由此说明本文建立的风能转换系统T-S模糊模型是有效的。
3 风能转换系统T-S模糊控制器的设计
基于风能转换系统的T-S模糊模型,利用普通二次Lyapunov函数(CQLF)的方法,给出风能转换系统的并行分配补偿(PDC)模糊控制器的设计方法。
3.1 T-S模糊控制器的设计
针对式(13),采用PDC控制策略,控制器输入的第i条规则:
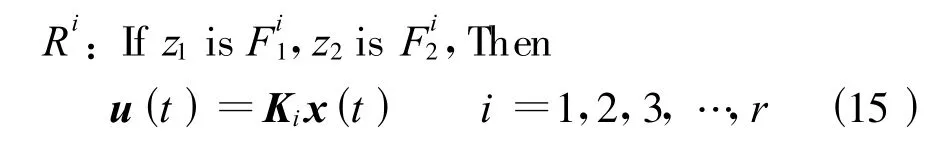
则模糊控制器如下:
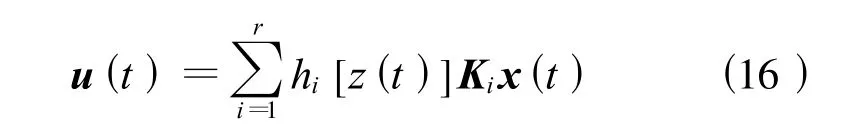
式中:Ki为第i个子系统的回馈增益矩阵,将式(16)代入式(14),得到闭环系统的全局状态方程:
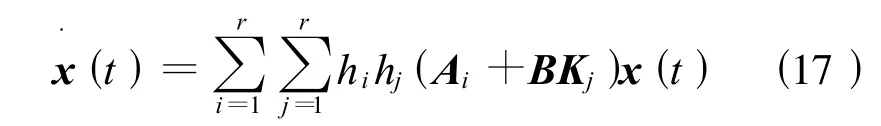
为确保上述控制器能够镇定模糊系统式(13),我们根据Lyapunov稳定性定理,得出如下定理。
定理1如果存在正定矩阵P,以及矩阵K1,…,Kr,使得下列矩阵不等式能够成立:

则式(16)能够使得模糊系统全局稳定。其中,r表示模糊规则数,X=P-1,Mj=Kj=X。
证明:定义Lyapunov函数如下:

求V[x(t)]沿式(17)的解轨线时间导数:

对式(18)和式(19)左右两边分别左乘以P和右乘以P,则转化为:

由于hi、hj≥0,可得此时,整个模糊控制系统在其平衡点处渐近稳定。证毕。
3.2 模糊控制器的求解
针对设计的模糊控制器式(16),由定理1可知,模糊控制系统的控制器设计和稳定性分析可归结为求解关于矩阵X和M可行性解的问题,这种凸优化问题可以利用LMI工具箱中的feasp求解器求解。
从本文的风能转换系统状态方程以及T-S建模过程可知,给定输入对风能转换系统的模糊控制器:

根据文献[11]的方法,有:


将式(20)代入式(21),得到最终的全局模糊控制器:

3.3 模糊控制器性能仿真
由表1提供的数据,我们可以得到线性方程组式(22)的解:

因此所得到的模糊控制器:

利用MATLAB中的LMI工具箱,求得回馈增益矩阵:
K1=[1.334 7 -3.919 9]
K2=[1.334 7 -3.919 9]
K3=[-0.237 3 1.065 5]
K4=[-0.237 3 1.065 5]
采用图5的风能转换系统闭环控制结构示意图,利用运算功能强大的Matlab/Simulink软件进行仿真,得到风速、风能转换系数、叶尖速比的波形如图6~图8所示。

图5 风能转换系统闭环控制结构示意图

图6 风速仿真图

图7 风能转换系数仿真图

图8 叶尖速比仿真图
由图6、图7、图8的风速、风能转换系数、叶尖速比仿真波形分析可知,基于T-S模糊建立的风能转换系统模型在模糊控制方法下响应快速且平稳,当风速大范围变化时,风能转换系数始终能够保持在最优值0.476附近小范围波动,控制效果较好;与最优值λopt=7相比较可见,T-S模糊控制方法下的叶尖速比λ可以维持在最优值附近,过渡平稳。
4 结 语
本文基于双馈风能转换系统的数学模型,以最大风能为目标,根据T-S模糊控制理论建立了风能转换系统的T-S模糊模型,并针对新的风能转换系统模型设计了模糊控制器;最后在Matlab/Simulink环境下进行了仿真,以验证控制方法的有效性。仿真结果表明,风速在额定风速以下大范围变化时,T-S模糊控制方法能够有效实现风能转换系统的最大风能捕获。
[1] 林宗虎.风能的利用[J].自然杂志,2008,30(6):309-314.
[2] 叶杭冶.风力发电机的控制技术[M].北京:机械工业出版社,2002.
[3] Steinbuch M.Dynamic Modeling and Robust Control of Wind Energy Conversion System[D].Delft University of technology,The Netherlands,1990.
[4] Munteanu I,Brarcu A I,Cutululis N-A.Optimal control of Wind Energy Systems[M].London:Springer,2008:28-135,150-158.
[5] Chadli M,Hajjaji A El.Wind energy conversion systems control using T-S fuzzy modeling[C]//18th Mediterranean Conference on Control&Automation,Marrakech,Morocco,2010:1365-1370.
[6] Takagi T,Sugeno M.Fuzzy identification of systems and its applications to modeling and control[J].IEEE Trans.on Systems,Man and Cybernetics,1985,15(2):116-132.
[7] Mishra S,Misha U,Li F,et al.TS-Fuzzy Controlled DFIG Based Wind Energy Conversion Systems[C]//IEEE PES General Meeting.Calgary,Canada,2009:978-984.
[8] Bianchi F,Battista H,Mantz R.Wind Turbine Control Systems[M].London:Springer,2007.
[9] 迟永宁,王伟胜.大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006,20(15):10-14.
[10] Iulian Munteanu,Nicolaos Antonio Cutululis,Antoneta Iuliana Bratcu,et al.Optimization of variable speed wind power systems based on a LQG approach[J].Control Engineering Practice,2005,13(7):903-912.
[11] Lian K Y,Liou J J,Huang C Y.LMI-Based Integral Fuzzy Control of DC-DC Converters[J].IEEE Transactions on Fuzzy Systems,2006,14(1):71-80.

