判别函数分析方法在评价网球比赛制胜因素中的应用研究

施兰平，白 刚，郭仲恺，孙卫星

(1.浙江工商大学 体育工作部，浙江 杭州 310018；2.北京体育大学，北京 100084)

判别函数分析方法在评价网球比赛制胜因素中的应用研究

施兰平1，白 刚1，郭仲恺1，孙卫星2

(1.浙江工商大学 体育工作部，浙江 杭州 310018；2.北京体育大学，北京 100084)

文章以84场男子网球比赛为研究对象，通过数理统计中的判别分析方法，筛选出网球比赛制胜的关键因子，为教练、运动员提供更有效的竞赛指导和训练状态诊断。研究结论显示：在男子网球比赛中一发成功率、一发得分率、二发得分率、接发球得分率为比赛获胜的关键制胜因子。

网球；比赛；制胜因素；判别函数

0 前 言

任何一场体育比赛在结束之后都会有各种技战术指标的统计结果，而教练员和运动员从这些指标中只能看出和对手之间在统计数值上的大小差距，这样的数值差距对比赛胜负到底存在多大影响呢？有没有一种方法能够帮助教练员和运动员从这些散乱的数据统计中找出对他们比赛获胜有帮助或者对训练有价值的东西呢？带着这样的问题，作者查阅了上百篇就数理统计方法与体育比赛技战术相结合进行研究的文献后发现，尚未有文章将数理统计与体育比赛制胜因素相结合进行研究。本文将以体育比赛中最常见的网球比赛为例，通过判别分析方法去筛选出网球比赛技战术统计项中对比赛获胜最有价值的关键制胜因子。通过这种方法，在网球比赛结束后，教练员和运动员就可以直接从十几项数据统计中找到真正对训练和比赛有意义的东西。本文将采用数理统计方法找到对比赛胜负影响最大的技术统计因子，并以此作为指标构建可以用于预测比赛胜负的函数方程模型，为教练、运动员提供更有效的训练状态诊断，也为网球科研工作者提供一种新的研究思路和方法。

1 研究对象与方法

1.1研究对象

以ESPN与CCTV5转播的2008年美国网球公开赛和2009年澳大利亚网球公开赛其中完整的84场男子单打比赛为主要研究对象。本文研究的因变量均为已明确分类的指标，并且所有变量间独立无共线性，因为判别分析对样本量的要求是为所用自变量的10～20倍以上，本文所统计的自变量在8～10个之间，因此样本量84场比赛完全具备统计分析要求。

1.2研究方法

1.2.1 文献资料法。通过查阅中国期刊网以及国内外关于网球比赛制胜因素的各种文献资料，全面了解网球制胜因素和技战术领域的发展现状和研究的最新动向。

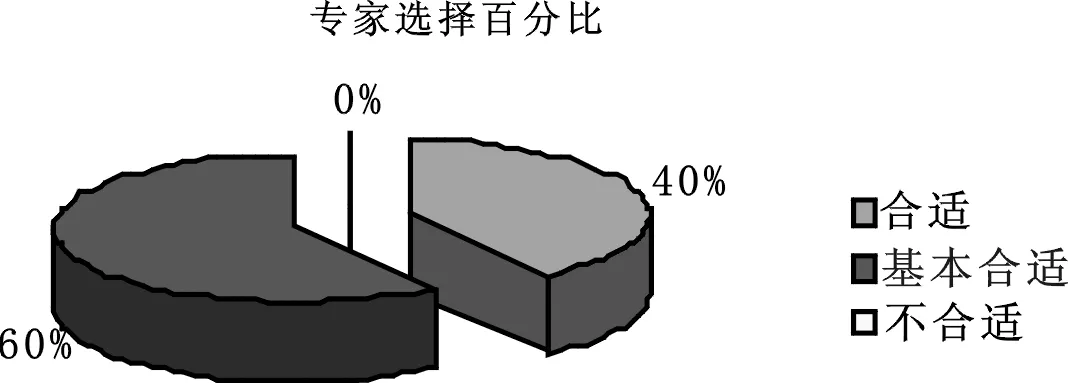
图1 专家效度检验结果

1.2.3 录像统计法。根据专家确定的10项指标，对所收集到的所有男子84场比赛利用慢放和定格等技术进行统计。

1.2.4 数理统计法。运用EXCEL中统计分析方法与SPSS 13.0中逐步判别分析方法对数据进行处理和分析。

2 研究结果

2.1判别分析统计方法说明

判别分析是一种比较常用的分类分析方法，它是研究事物分类的统计基本方法。从图2可以看出，判别函数分析方法是从已有分类结果的预测变量样本中提取信息，构建判别方程，根据判别方程对未知分类样本的分类做出判别。本文研究的主要内容是以网球比赛中各项技战术指标为预测变量，以是否获得比赛胜负作为组别变量，进行判别函数分析，判断未知变量的比赛胜负组别。

图2 判别函数分析示意图

2.2网球比赛技战术统计项专家调查情况

一场网球比赛结束之后，官方或者教练所统计的技战术指标有很多，而从网球技战术书籍上查处能够代表男子网球比赛技战术特点的指标也有很多，通过这些网球技术文献并结合ATP以及ITF常用统计比赛胜负影响的指标做出专家调查问卷，让专家去选择能够代表网球技战术特点的指标，一共发送问卷20份，回收18份，根据对18份有效问卷的调查结果，筛选出网球专家、教练员和运动员认为能够代表男子网球技战术的10项关键指标(超过调查人数2/3的就认为该指标适合)，最后确定分别是一发成功率，Aces，双误，非受迫性失误，一发得分率，二发得分率，主动得分，接发球得分率，破发点得分率，网前得分率。专家对指标的确定人数如图3。

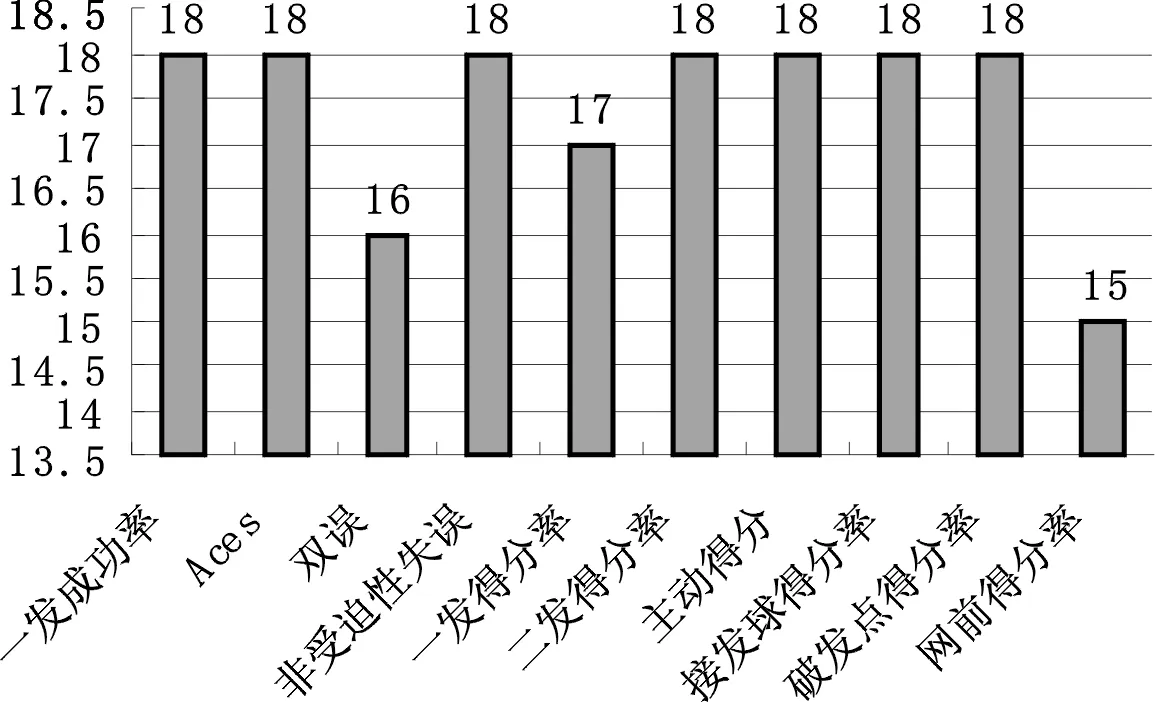
图3 专家确定的指标的人数统计

2.3对专家所选指标的确定

11月15日，全国新农民新技术创业创新博览会在江苏南京开幕。开幕当天举办了全国新农民新技术创业创新论坛，农业农村部部长韩长赋强调，党中央、国务院高度重视农村“双创”，各地各有关部门要认真贯彻习近平总书记重要指示精神和中央部署要求，发挥好新农民新技术的引领示范作用，努力打造农村“双创”升级版，为实施乡村振兴战略、加快农业农村现代化作出新的更大贡献。博览会为期4天，期间将举办全国农村创业创新项目创意大赛等10多场活动。 （来源：中国农业新闻网）

专家所选择的这些指标到底有多大的代表性？最简单直接的方法就是通过比赛胜负彼此之间的显著性差异大小来进行检验，如果专家所选择的这些指标在比赛胜负的时候，结果有显著性就说明有代表意义，没有显著性差异说明所选择的指标在后面的分析当中没有什么价值。

2.3.1 对专家所选指标的方差齐性检验。方差齐性检验是做T检验前必不可少重要一步，本文主要想通过判别函数检验去找出10项指标中对比赛胜负影响最大的因子，而做T检验是为了提前验证所选指标的代表性。本文研究对象之间一共是84场比赛，将胜负双方的10项数据结果通过独立样本T检验进行分析，在T检验时由于两个正态总体的方差齐性和不齐性时，构造的检验统计量不同，所以在未知正态总体的方差信息时，必须首先通过SPSS列文方差F一致性检验，在F值齐性和不齐性时所对应的T值存在不同，本研究最终F检验见表1。

表1 列文方差F一致性检验

2.4专家所选指标的描述统计

根据专家确定的一发成功率，Aces，双误，非受迫性失误，一发得分率，二发得分率，主动得分，接发球得分率，破发点得分率，网前得分率这10项网球技战术指标，在统计了84场比赛后，将所有指标汇总进行计算与分析，最后得出10项指标在比赛胜负时的差异性，见表2。从表2可以看出所选择的11指标在比赛胜负时都存在显著性差异，这样的显著性差异有两点意义：①可以充分说明专家所确定这些指标的准确性，没有显著性差异就说明所选指标是没有价值的。②从这里还可以看出进行逐步判别分析的重要性，因为这10项指标到底是哪几项指标对比赛胜负影响最大，教练员和运动员无法从这10项指标中得到真正有价值的东西。

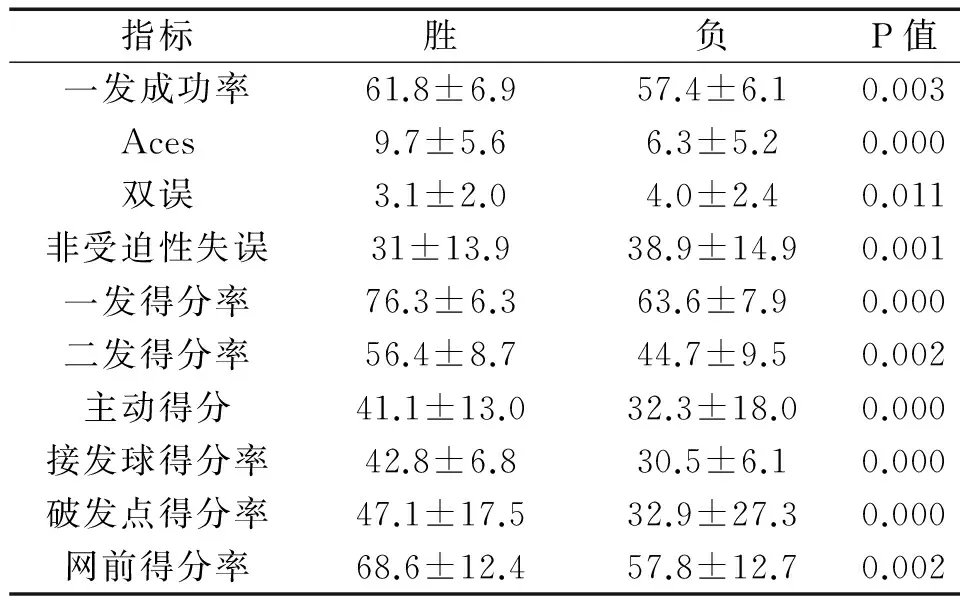
表2 胜负比赛技战术指标描述统计

2.5制胜关健因子的筛选与胜负判别方程的建立

2.5.1 判别分析前所选因子之间的相关性分析。准备建立可以判断比赛胜负的判别函数方程之前，为了确保判别函数方程的稳定性及预判比赛胜负的准确性，在做判别分析过程中需要对10项变量之间的相关性进行检验。从表3可以看出各个因子之间的独立性还是比较理想的，符合统计学意义。一发成功率，Aces，双误，非受迫性失误，一发得分率，二发得分率，主动得分，接发球得分率，破发点得分率，网前得分率这10个因子之间的独立性还是比较理想的，相关性系数最大的主动得分和ACE球正相关系数为0.581，属低度相关。由此可以认定，带入判别分析的各技术统计项之间的独立性非常理想(全部均为低度相关)，很适合进行判别分析，这样在进行组间检验的时候就会大大减少相互之间的影响，因此这10项指标之间的相关性符合统计学意义。

表3 技术统计项之间的相关性

2.5.2 建立判别函数前的组共变异数假设检验。组共变异数假设检验是做判别函数分析前最重要是一步，从组共变异数数值大小上可以看出所选择样本量是否达到了统计学要求，进行下一步分析是否有较大意义。目前，建立判别函数分析的组共变异数假设检验通用的是Box's M检验，在对样本进行Box's M检验的时候，主要看的是相伴概率的显著性(Sig.)，如果显著性(Sig.)<0.05达到显著性水平，则说明所统计两组数据共变异数不相等，这是不符合判别分析的假定，因此在后面进行统计分析的时候就得需要谨慎注意。从表4可以看出，在本文所研究的两组样本中，这10项指标间的Box's M值为8.495，F值为0.827，相伴概率为0.602，达到了显著性水平，因此两组样本间的共变异数相等，这是符合判别函数的假设的，因此两组样本间做判别分析有意义。

表4 判别函数Box's M检验

2.6判别函数方程的建立

2.6.1 制胜关键因子的得出与判别函数方程的建立。在采用SPSS软件包判别分析中的逐步判别方式时，结果将输出判别分析筛选出的N项变量的标准化系数，这N项就是制胜因子，也就是对判别胜负影响最大的几项技术统计。

从表5可以看出经过对10项技战术统计的逐步判别分析，最终筛选得到了4个因子。根据判别分析的基本原理结合实际情况，这4项带有标准化系数的技术统计项就是男子网球单打比赛的制胜关键因子，每个因子后面所对应的值就是分类函数系数。从下表5的结果可以看出，一发成功率、一发得分率、二发得分率、接发球得分率在比赛获胜的判别系数分别为1.306、1.287、0.471和0.834。根据非标准化判别函数的判别结果，给出四项关键因素的系数和常数，建立比赛获胜时的非标准化的判别方程如下：

Y=1.306X1+1.287X2+0.471X3+0.834X4-212.85

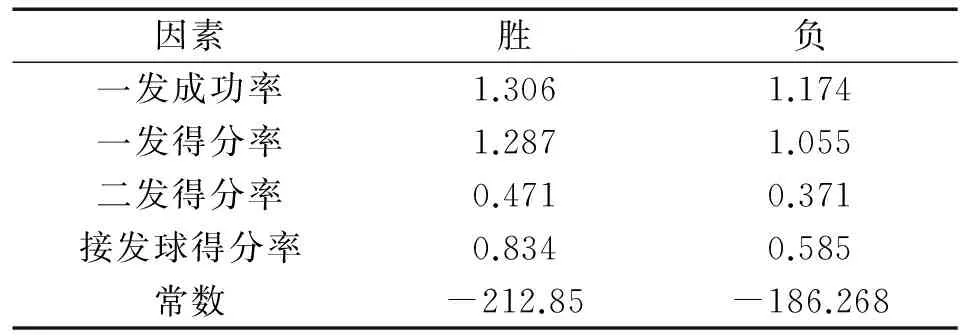
表5 分类函数系数

2.6.2 分组函数重心的意义。分组重心函数用在判别分析区域图中重点是为了区别胜负组别，就是在一张图中两者之间的分界点和范围，从表6可以看出，比赛获胜时的函数重心为1.388，因此可以说判别函数方程建立后将有代表性的因子带入方程中，与1.388这个值越接近，越有希望赢得比赛。而与-1.388越接近则说明越有可能输掉比赛。

表6 各组的函数重心

2.7判别方程的准确率检验

判别效果的检验是判别函数的重要步骤，从表7判别分析分类结果矩阵可以看出，该方程对比赛胜负影响的一致性判断为94%以上，对获胜判断为96%以上。此外，本研究将2008年北京奥运会男子单打比赛数据带入判别方程Y=1.306X1+1.287X2+0.471X3+0.834X4-122.85外带验证样本准确性到达了93. 2 %。说明运用判别分析建立起来的判别函数方程，对预测男子单打比赛的胜负具有较好的准确性。

表7 判别效果的分类矩阵

2.8判别方程预测的程序与方法以及实际运用

本研究得出的判别函数方程(Y=1.306*一发成功率+1.287*一发得分率+0.471*二发得分率+0.834*接发球赢球率-212.85)，该方程适合所有的男子网球比赛。在实际运用的时候将球员比赛时的一发成功率、一发赢球率、二发得分率、接发球赢球率4项指标代人方程求出Y值，然后将Y值与表6中的函数重心值进行比较。如果Y值与胜(1.388)更为接近，即Y>0时，可判定球员获胜，如果Y值与 (一1.388)更为接近，即Y<0时，可判定这球员失利。

此外在实际运用的时候，判别方程中变量的标准化系数越大，表明该变量对判别函数影响越大。由此可见，在本研究中这4项技术统计对胜负影响的大小依次为:一发成功率>一发得分率>二发得分率>接发球赢球率。根据这样的胜负影响大小，教练员和运动员在赛后对比赛进行分析总结或者在准备下一场次比赛的时候，可以将对手或者自己队员的多场比赛数据统计好，利用判别函数分析，找到对手通常在比赛中的制胜因素，这样在赛前可以有针对性的准备。

3 结 论

3.1 首次利用数理统计方法筛选出了男子网球比赛制胜的关键因子，对于男子网球训练和比赛都有较大意义，为以后的网球训练和科研工作提供了一种新方法。

3.2 世界优秀男子网球比赛中一发成功率、一发得分率、二发得分率、接发球得分率是对比赛胜负影响最大的因子，这四个因子是运动员和教练员在训练和比赛中应该关注的重点。

3.3 由判别分析所筛选出制胜因子建立的方程，用于预测男子网球单打比赛胜负准确率在94%以上。

[1] Darren Cabill.Tactics of the Baseline Player.Coaching﹠Sport Science Review[C].10th Year Issue 27.Auguest 2002.

[2] 陈正, 陈莉, 孙江宁.国家女网周课训练安排及训练效果实时监控分析[J].体育学刊,2007(2).

[3] 杨新芳,许伟民.羽毛球竞赛女双项目的制胜规律[J].体育学刊,2005(2).

[4] 李方晖,刘承宜，等. 队服颜色影响体育比赛成绩的内稳态研究[J].体育学刊,2008(12).

[5] 胡亚斌.优秀男子职业网球选手技战术运用特征的研究[D].北京体育大学,2005.

[6] 唐小林,陶志翔，等.我国网球男子双打竞技水平现状及对策研究[J].北京体育大学学报,2006,29(5).

[7] 王艳,刘娟妮.2006年澳网女子双打决赛技战术分析[J].武汉体育学院学报,2006,40(6).

[8] 孙卫星．现代网球技术教学法[M]．北京：北京体育大学出版社，2007：158-160.

[9] 余建英，何旭宏．数据统计分析与SPSS应用[M]．北京：人民邮电出版社，2003：102-116.

[10] 李志辉，罗平.SPSS for Windows 统计分析教程[M].第2版.北京：电子工业出版社，2005：335-355.

[11] 付饶，孙卫星．硬地女子网球双打比赛三项指标实力评估法的建立与应用[J]．中国体育科技，2008(4).

ResearchonKeyFactorsofWinningtheTennisGamebyDiscriminantAnalysis

SHI Lan-ping1,BAI Gang1,GUO Zhong-qi1,SUN Wei-xing2

(1.Sport Working Department，Zhejiang Gong Shang University,Hangzhou 310018，China;2.Beijing Sport University,Beijing 310018,China)

The aim of this study is 84 ATP games,through using the method of discriminant analysis.This paper can select indexes which has big influence on wining and losing of tennis match from common technical statistics of tennis match. Player and coach can get a lot of help from this method. The result shows first serving percentage, first serve winning percentage, second serve winning percentage, receiving points won are key factors to win the game and the accuracy of its judgment as high as 94%.

tennis;contest;key of winning factors;discriminant analysis

2011-03-28

施兰平(1981-)，男，江苏人，助教，硕士，研究方向为体育统计学.

1004-3624(2011)05-0087-04

G80-32

A