基于偏微分方程的CT图像分割及其MATLAB实现

周应杰，吴海坚

广州医学院附属肿瘤医院， 广东 广州 510095

基于偏微分方程的CT图像分割及其MATLAB实现

周应杰，吴海坚

广州医学院附属肿瘤医院， 广东 广州 510095

CT图像在医学影像领域的应用最为广泛，CT图像的分割对病变区域的提取、组织定位、组织测量以及实现三维重建有着非常重要的作用。近年来，基于偏微分方程的图像分割作为一种比较新颖且有效的图像分割方法，逐渐成为研究的热点。本文对基于偏微分方程(PDEs)的GAC和C-V两种图像分割模型进行了探讨，利用MATLAB语言编程实现，并结合实际CT图像进行了实验研究，为这些模型在CT图像的分割上的应用提供科学依据。

CT图像；CT图像分割；偏微分方程；GAC模型；C-V模型

0 前言

图像分割一直是图像处理研究中的重要任务和热点问题，它早已被广泛地应用于医学图像处理之中[1]。近十几年来，随着偏微分方程方法在图像处理中应用的兴起，图像分割的偏微分方程方法也逐步取得了很大的进展。图像分割可以理解为将图像中有意义的特征区域或者需要应用的特征区域提取出来，这些特征区域可以是像素的灰度值、物体轮廓特性曲线、纹理特性等，也可以是空间频谱或直方图特征等[2]。医学图像分割是医学图像处理和分析中的关键技术，分割后的图像被广泛应用于组织的定量分析、诊断、病变组织的定位、解剖结构的学习、治疗规划、功能成像数据的局部体效应校正和计算机指导手术等[3]。随着影像医学在临床医学的成功应用，图像分割在影像医学中发挥着越来越大的作用[4]。CT图像是利用计算机技术处理人体组织器官得到的切面显像，它可清晰地显示人体内的组织结构。CT技术作为一种先进的疾病诊断手段，广泛应用于医学领域中，但是由于医学图像具的复杂性和多样性，使得对CT图的分割很困难。目前很多学者致力于此方面的研究，取得了很多成果，但至今还没有找到一种十分满意的方法应用于临床医疗[5]。

1 传统的图像分割方法和基于PDE的图像分割模型

在传统的图像处理技术中，已经有相当多的研究成果和方法，这些方法可以归为3大类：基于区域的分割方法、基于边缘的分割方法和基于阈值的分割方法[6-7]。基于阈值的分割方法相对简单，计算量小，稳定性较好，但抗干扰能力不强，对目标和背景灰度有梯度变化的图象效果较差。基于区域的分割方法，依赖于图像的空间局部特征，如灰度、纹理及其他像素统计特性的均匀性等。典型的基于区域的分割方法有区域生长、区域分裂以及区域生长与分裂相结合的方法等，由于这些方法直接依赖于图像的灰度值，因此它们的主要优点是对噪声不敏感，但这些方法常会造成图像的过分分割问题，并且分割结果较大程度上依赖于种子点的选择，分割所得到的区域的形状也依赖于所选择的分割算法。基于边界的分割方法主要是利用梯度信息确定目标的边界，包括局部微分算子、Roberts算子、Prewitt梯度算子、canny算子和Laplacian二阶差分算子等。这些方法不依赖于已处理像素的结果，但缺点是对噪声敏感，而且当边缘像素值变化不明显时，容易产生假边界或不连续的边界[8]。针对不同领域的应用，相继又提出了基于统计学的方法、基于小波变换的方法、基于信息论的方法、基于模糊分割的方法、基于神经网络的方法和基于遗传算法的方法等，每种方法都有它的局限性。

为了克服传统的图象处理方法的缺陷，近年来人们提出了基于偏微分方程的图象分割方法，此方法主要是采用活动轮廓模型来实现图像分割[9-10]。1987年Kass M等人共同发表了题为“Snake：Active Contours”的论文[11]，首次提出了运用活动轮廓模型进行2D和3D图像分割的思想。该模型得到迅速发展，逐渐成为最有活力和最成功的图像分割技术之一。

1.1 测地线活动轮廓模型（GAC模型）

活动轮廓模型（Active Contours）的基本思想是将图象分割问题归结为最小化一个封闭曲线C(p)的能量泛函[12]：

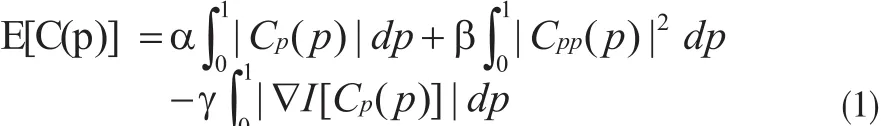
根据曲率运动演化的性质，可以略去第二项，为避免第三项的负号，可引进一个新函数g(r)，r∈R+，(1)式可改写为：

此模型存在严重缺陷，它不仅依赖于曲线C的几何形状和位置，而且还依赖于曲线的参数p，为了克服此缺陷，Caselles V等人[10]于1997年提出了不含自由参数的测地线活动轮廓（Geodesic active contours，GAC）模型，该模型的提出是PDE（偏微分方程）方法在图像分割中的重大突破。该模型以最小化以下能量泛函来确定活动轮廓：

上式中是闭合曲线C的加权弧长，由于以上泛函是建立在曲线固有参数弧长之上的，因而它消除了经典蛇模型依赖自由参数的缺陷。可以证明最小化(3)式对应的梯度下降流为：

即(4)式为GAC模型式。曲线按照此式演化时将受两种“力”的支配：① 来自曲线自身曲率运动的“内力”，它受图像I(x,y)梯度标量场g(x,y)的控制，在图像边缘这种力变得很小。② 来自于g(x,y)的梯度▽g，由于g(x,y)=g(|▽I(x,y)|)，▽g是由图像I(x,y)产生的，所以第二项力称为外力。它能使C向对象的边缘靠近，并稳定在边缘上。从以上分析可知GAC模型存在一个局限性，即当图像中存在较深的凹陷边界时，GAC模型将使C停止在某一能量局部极小值状态，并不与对象边界一致。此时若在(4)式中再增加一个收缩力，使C遇到较深的凹陷时继续收缩，于是GAC模型改造为：

式中c为一可选常数，(5)式为推广的GAC模型。

1.2 无边缘活动轮廓模型（C_V模型）

如果图像既没有明显的边缘，又缺乏明显的纹理特征，利用以上讨论的GAC模型将难以成功的分割。Chan和Vese提出的基于简化Mumford-Shah模型和水平集方法相结合[12]可以有效地用于此类图像分割。其思路是，如果能找到闭合曲线C将图像分为内部Ω1和外部Ω2，使Ω1和Ω2的平均灰度值恰好反映出对象与背景之间的灰度平均值的差别，那么这一闭合曲线C就可以看作是对象的轮廓，其能量泛函如下：

上式称为无边缘活动轮廓模型（Active contours without edges， 或称C-V模型），其中第一项为C的弧长，第二和第三项为内部和外部的灰度值与标量C1和C2的平方误差，只有当C达到正确位置时这两项的值才能同时达到最小。

采用水平变分集方法，先在(6)式引入Heaviside函数，将它修改为关于嵌入函数u的泛函：

这样在函数u固定的条件下相对C1、C2最小化式(7)，可得：

C1、C2分别是输入图像I（x,y）在Ω1（曲线内部）和Ω2（曲线外部）的平均值。在C1、C2固定的条件下，相对于u最小化式(7)可得：

于是通过连立方程(8)和(9)求稳态解，便得到分割结果。

1.3 基于PDE方法对CT图像分割的实现

1.3.1 GAC模型的数值解法及实验结果

本文采用迎风方案实现推广GAC模型的水平集方法，限于篇幅，在此不详细列出，这里只给出结果，具体理论方法可以参考微几何及参考文献[13-14]。图1和图3分别是原始的脑部和体部CT图，图2和图4分别是对应分割后的脑部和体部CT图，明显看出，由于GAC模型的特点，此方法最多只能把整个图像从背景中分割出来，且分割边缘也不太理想。

图1 脑部原始CT图

图2 分割后的脑部CT图

图3 体部原始图

图4 分割后的体部图

1.3.2 C_V模型的数值解法及实验结果

本文采用半隐式方案实现变分水平集图像分割方法中的“C-V”模型(Active contour without edge)[14]。如图5和图7分别是原始的脑部和体部CT图，图6和图8分别是对应分割后的脑部和体部CT图。从实验结果来看，脑部CT图基本可以将脑室正确地区分出来，体部CT图可以非常正确地分割出器官的位置，“C-V”模型用于CT图像的分割能够得到较为理想的结果。

图5 脑部原始CT图

图6 分割后的脑部CT图

图7 体部原始CT图

图8 分割后的体部CT图

2 小结

基于偏微分方程的图像分割方法确实是一类很有发展前景的方法：

（1）使用偏微分方程可以用广义上连续的二维函数对图像进行建模，从而可对图像进行求导求积分运算，使图像处理问题规范化。

（2）可以很好地利用现在一些非常完备的数值分析和偏微分方程计算方法来进行运算[15-16]。

（3）使用偏微分方程可以使图像分割的速度，准确性和稳定性大幅度提高。

医学图像分割技术仍然是制约医学图像处理中其他相关技术发展和应用的一个瓶颈。医学图像分割技术是开展医学图像在临床和生命科学研究领域广泛应用的一个先行程序，CT图像分割由于被用于临床医疗，因此CT图像分割的准确性更为重要。现在，医学图像分割的算法大多是把多种理论结合起来应用，以达到相互补充的目的。目前，新的分割方法的研究主要以自动、精确、快速、自适应性和鲁棒性等几个方向作为研究目标，偏微分方程方法在这些方面的应用具有广阔的前景，新的偏微分方程模型的研究有待进一步努力。

[1] Wells W M,Grimson W E L,Kikins R,et al.Adaptive segmentation of MRI datap[J].IEEE Trans.on Medical Imaging, 1996,15(4):429-442.

[2] 田捷,包尚联,周明全.医学影像处理与分析[M].北京:电子工业出版社,2003:35-37.

[3] Dzung L Pham,Chenyang Xu,Jerry L Prince.A Survey of Current Methods in Medical Image Segmentation[R].Technical Report JHU/ECE 99-01,Johns Hopkins Univ,1998.

[4] James S Duncan,Nicholas Ayache.Medical Image Analysis: Progress over Two Decades and the Challenges Ahead[J].IEEE Transaction on patter analysis and machine intelligence,2000,22 (1):181-204.

[5] 李景,等.医学图像分割技术[J].生物医学工程学,2006,23(4): 891-894.

[6] 章毓晋.图像分割[M].北京:科学出版社,2001.

[7] 章毓晋.图像处理和分析[M].北京:清华大学出版社,1999.

[8] 吴月娥,周康源,李传富,等.基于level sets的医学图像分割[J].北京生物医学工程,2006,(3):240-243.

[9] Castlemen K R.Digital Image Processing[M].Prentice Hall,1996.

[10] Caselles V,Kimmel R,Sapiro G.Geodesic active contours[J]. International Journal of ComputerVision,1997,22(1):61-79.

[11] Kass M,Witkin A,Terzopoulos D.Snakes:active contour models[J].International Journal of Computer Vision,1988,(33): 321-331.

[12] Chan T F ,Vese L A.Active contours without edges[J].IEEE Trans.Image Processing,2001,10(2):266-277．

[13] 李荣华.偏徽分方程数值解法[M].北京:高等教育出版杜, 2005.

[14] 王大凯,侯榆青,彭进业.图像处理的偏微分方程方法[M].北京:科学出版社,2009.

[15] 李玲,等.基于改进的Snake模型分割肝脏的CT图像[J].中国医疗设备,2010,25(2):19-20.

[16] 张宜,陈刚.基于偏徽分方程的图像处理[M].北京:高等教育出版,1990:629-639.

CT Image Segmentation Based on Partial Differential Equation and Programming in MATLAB

ZHOU Ying-jie,WU Hai-jian
The Affiliated Tumor Hospital of Guangzhou Medical University, Guangzhou Guangdong 510095, China

CT images are widely used in medical science. CT image segmentation is important for disease area extraction, tissue location, tissue measuring, and three-dimensional reconstruction. Recently, image segmentations based on partial differential equation(PDE),which is one of the novel and efficient segmentation ways, are gradually turned into research hotspot. In this article, we study in GAC model and C-V model based-PDE image segmentation. The arithmetic of the paper is carried out by programming in matlab,and is verified effectively.

CT images; CT image segmentation; partial differential equations; GAC model; C-V model

R318

B

10.3969/j.issn.1674-1633.2011.05.060

1674-1633(2011)05-0159-03

2010-08-23

2011-03-23

作者邮箱：zhouyingjie@tom.com