基于加权最小二乘谱迭积算法探测超导重力观测弱信号＊

尹 晖 王艳艳

(武汉大学测绘学院,武汉 430079)

基于加权最小二乘谱迭积算法探测超导重力观测弱信号＊

尹 晖 王艳艳

(武汉大学测绘学院,武汉 430079)

提出采用加权最小二乘谱迭积算法探测超导重力观测数据隐藏的弱周期信号,该算法基于不等权的观测序列和序列的自相关性和互相关性,以高分辨率提取序列潜在的共同信号,削弱或抵消噪声信号。并以实例进行了分析和验证。

加权最小二乘谱分析;谱迭积;超导重力数据;弱信号;噪声

1 引言

超导重力仪具有稳定性强、灵敏度高、噪音低、漂移小等特点,可以提供精度为 10-11ms-2的重力观测数据,为地球深内部构造和核模弱信号检测等研究提供了有效途径。但由于超导重力仪观测数据受大气环境、地震和仪器干扰如断电,维修、调试、系统升级、氦注入等多种因素的影响,观测数据会出现不连续和不平稳等现象,对存在断链、尖峰、基准偏移、不等权、不等间隔等情况下的重力观测数据,采用最小二乘谱分析进行处理已显示出较大的优越性[1]。

但由于核模等信号很弱,对掩盖在噪声背景下的弱信号仅采用谱分析仍很难检测到。本文提出采用基于加权最小二乘谱迭积算法来探测超导重力观测数据隐藏的弱周期信号。该算法能考虑观测序列和序列的自相关性和互相关性,以高分辨率提取序列潜在的共同信号,削弱或抵消噪声信号。并以加拿大超导重力观测站实测数据进行了分析验证。

2 加权最小二乘谱迭积算法

2.1 加权最小二乘谱分析

给定一组观测值向量 f=f(t){fi}(i=1,2,…, n),该观测值向量可能存在断链、尖峰、基准偏移、不等间隔、不等权等情况,设观测值向量具有协方差阵 Cf,建立如下模型：

根据最小二乘谱分析原理[2],得加权最小二乘谱的计算公式为

若设定基函数形式为一组频率为ωi,i=1,2,…,m的三角函数,则对于不同的频率,可以得到不同的频谱值:

2.2 谱迭积算法

谐波谱积算法是将交叉谱的思想推广应用到多个不同时间序列的联合谱分析上,以反映多个相同时段的不同时间序列在频域变化上的相互关系,将不同时间序列在相同频率段对应的频谱值相乘,能够对不同时间序列计算得到的同一频率处的信号起放大作用,从而将掩藏在噪音中的信号迭积检测出来。

Smylie D E[3]1993年应用快速傅立叶变换和谱迭积方法检测欧洲 3个台站的超导重力观测数据中的弱重力共振信号。类似地,Vanicek P[4,5]提出将最小二乘谱分析应用到多个时间序列的联合谱分析上,进行谱迭积,由公式 (4),给出在指定频率区间[ω1,ω2]内,谱迭积的计算公式为:

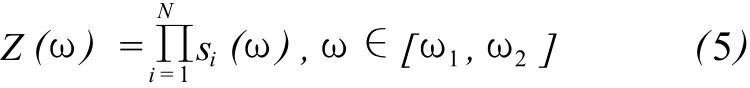
式 (5)是N个时间序列的谱积,si(ω)是第 i个时间序列的最小二乘谱,从式 (5)可以看出,对于序列中潜在的共同信号,经过谱迭积计算后,谱值以高分辨率得到增强,而对于序列中的噪声信号,由于其出现的随机性和不确定性,其迭积后的谱值将得以削弱或抵消。

3 实例分析

3.1 数据处理与分解

加拿大超导重力观测站实测数据为 1 s的采样率,对实测数据采取如下的处理步骤[4]：1)数据获取。对以天为 1个记录文件、采样率为 1 s的原始数据(单位为V)进行转化 (乘以 -78.48×10-5m/ s2V转化为重力单位 10-5ms-2),删除重叠数据,使数据序列的时间单位呈单调递增,合并成以年为单位的数据文件;2)重力潮汐影响剔除。根据重力潮汐预测程序 G-wave[6]计算得到重力潮汐理论结果来剔除超导重力原始观测数据中的重力潮汐信号的影响;3)数据过滤。采用滞后窗为 50 s的 Parzen窗作为权函数,最大步长为 100 s进行随机采样,为避免数据间的相关性,要求两个连续窗不能叠置,这样每小时大约得到 24个不等间隔的过滤数据,由窗函数按误差传播定律计算得到其方差,因而得到不等权,不等间隔的随机观测序列;4)数据分解。针对本项目研究感兴趣的弱信号位于周期 2～10小时之间,按照 Nyquist采样定理,我们将全年数据分解为以月为单位时段(12个月),其目的是利用时间序列的随机性、非平稳性和自相关性,运用谱迭积多尺度地检测出隐藏在所有时间序列中的共同信号。

3.2 计算与分析

对 1998年 12个月不等间隔和不等权值的超导重力观测数据序列,运用加权最小二乘谱分析模型进行计算,得到最小二乘谱图,图 1、2给出计算的部分谱图,从图中可见,由于超导重力观测受噪声信号的影响,信号具有明显的随机性和不确定性,要分辨和检测到超导重力观测数据中的弱信号很难,不同月份谱分析计算的结果没有明显的对应比较关系,一致性较差,根本无法判断检测信号的结果。

对此,在谱分析计算的基础上,运用谱迭积算法对超导重力观测数据的最小二乘谱分析结果进行谱迭积,图 3给出了 1998年超导重力观测数据的最小二乘谱迭积后的结果,从图中可见,在经过谱迭积计算后,谱值的分辨率得到大大增强,而序列中的噪声信号,由于其出现的随机性和不确定性,其迭积后的谱峰得到削弱或抵消。应用最小二乘谱迭积分析方法分析加拿大 6年 (1997—2002)实测超导重力观测数据的弱信号,进行了地球内核 Slichter模谱峰信号的检测[1],表 1给出了 90%置信水平下的检测结果,其结果与 Smylie的结果[7]较为接近。

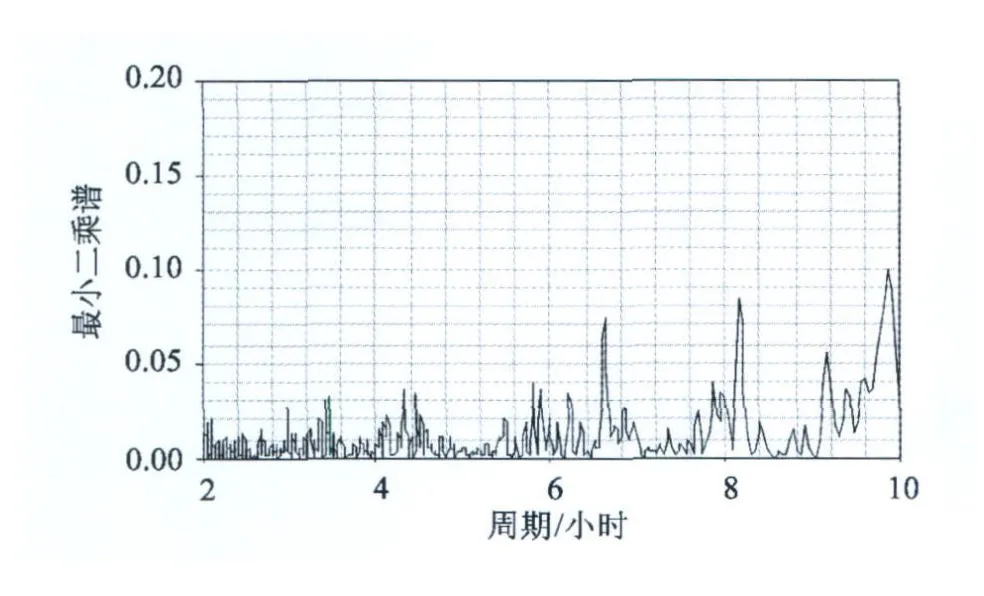
图 2 1998年 2月的最小二乘谱图Fig.2 Least square spectrum in Feb.1998

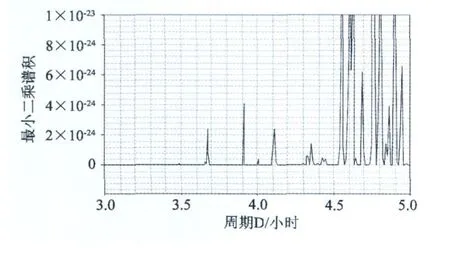
图 3 1998年加权最小二乘谱迭积图Fig.3 Product ofweighted least square spectrum in 1998

表 1 Slichter模谱峰检测结果(单位:小时)Tab.1 Test results for spectrum peak of Slichter mode(un it:hour)

4 结语

1)基于最小二乘谱分析技术,无须内插缺失的数据,无须平滑尖锋和漂移,直接由加权最小二乘谱分析得到谱值,从而避免了不必要的数据处理,而使隐藏在序列中的有效信息受到损失。

2)对超大量数据进行过滤,在整个数据段上对所有数据进行融和,并以加权处理提取时间序列的有效信息,是数据融合和信息挖掘的一种有效方法,过滤数据为不等间隔,其方差由窗函数按误差传播定律得到。

3)基于加权最小二乘谱迭积算法探测超导重力观测数据隐藏的弱周期信号,可以顾及观测序列和序列的自相关性和互相关性,从而削弱或抵消了超导重力观测数据中的噪声信号,增强谱值的分辨率。

4)Slichter模信号检测是目前地学界研究的热点之一,本文利用超导重力观测数据,运用最小二乘谱迭积方法检测 Slichter模信号的研究结果表明,该方法是地球深内部弱信号检测的有效方法,为进一步研究地球深内部结构及其动力学现象提供了新的途径。

1 SpirosD,et al.Least-squares self-coherency analysis of superconducting gravi meter records in search for the Slichter triplet[J].Phys Earth Planet Int.,2007,160：108-123.

2 Pagiatakis SD.Stochastic significance of peaks in the leastsquares spectrum[J].Journal of Geodesy,1999 73：67-78.

3 Smylie D E,et al.The product spectra of gravity and barometric pressure in Europe[J].Physics of the Earth and Planetary Interiors,1993,80：135-157.

4 Vanicek P.Approximate spectral analysis by least-squares fit [J].Astrophysics and Space Science,1969,4：387-391.

5 Vanicek P.Further development and properties of the spectral analysis by least-squares[J].Astrophysics and Space Science,1971,12：10-33.

6 Yin Hui and SpirosD Pagiatakis.Least squares spectral analysis and its application to superconducting gravimeter data analysis[J].Geo-Spatial Information Science,2004,7(4)：279-283.

7 Smylie D E,et al.The Inner core translational triplet and the desity near earth’s center[J].Science,1992,255：1 678 -1 682.

DETECTI ON OF W EAK SUPERCONDUCTING GRAVI M ETRIC SIGNALSW ITH PRODUCT SPECTRUM OF W EIGHTED LSSA

Yin Hui andWang Yanyan
(School of Geodesy and Geom atics,W uhan University,W uhan 430079)

Least Squares SpectralAnalysis(LSSA)has been shown more suitable than Fourier analysis for analyzing time serieswith spikes,gaps,datum shrifts(offsets)and other disturbances in a variety of applications in geodesy and geophysics.To detect the weak superconducting gravimetric signals,a methodology of product spectrum based on weighted LSSA is presented,which can take consideration the correlations among the signals and highlight the potential spectra power of high resolution in the common figures as well as weaken or eliminate the power of noise.A data set of superconducting gravi meter observations at the Canada Superconducting Gravi meter Installation(CSGI)has been assembled for analysis to show its efficacy.

weighted LSSA;product spectrum;superconducting gravimetric data;weak signals;noise

1671-5942(2011)04-0063-03

2011-02-19

国家自然科学基金(51077105);国家电网公司科技项目(SGKJ2009-0609-51)

尹晖,女,1962年生,教授,博士,博导,主要从事变形监测分析与预报、超导重力数据分析及地球动力学研究.E-mail：hyin @sgg.whu.edu.cn

P207

A